Generation of high-frequency combs locked to atomic resonances by quantum phase modulation

Precision spectroscopy is undergoing a revolution driven by the invention of frequency combs. These combs represent a 'ruler' of equidistant spectral lines and now allow us to create a fully phase-locked link from radio frequencies through the infrared, visible, all the way up into the extreme ultraviolet (XUV) spectral region [1–3]. Frequency combs have set off several disruptive developments in various fields, including optical clocks [4], attosecond control of electronic processes [5], precision distance measurement [6], astronomical spectroscopy [7], the quantum control of multilevel atomic systems [8, 9], and the laser cooling of molecules [10]. Optical frequency combs were first generated by intra-cavity phase modulation [11, 12]. Later, large-bandwidth combs were demonstrated that exploit the comb-like frequency structure of mode-locked lasers with stable repetition rate and carrier–envelope phase [13]. This generation scheme was also transferred into the XUV spectral region utilizing high-order harmonic generation (HHG) [1, 14, 15].

Meanwhile, at x-ray frequencies, rapid progress in free-electron laser (FEL) science now provides laser-like ultrashort light pulses at high intensities [16]. Unfortunately, x-ray precision metrology has not yet entered the mainstream of FEL science, which would change dramatically if frequency combs could be realized at such x-ray sources. To date, high-precision measurements still rely on spatial geometry–based crystal monochromators [17]. However, exploring transitions in highly charged ions (HCIs) [18] demands for higher precision, allowing fundamental physics applications such as sensitively testing bound-state QED effects [19] or the probing of heavy-ion nuclear structures by inner-shell electrons [20]. Also the search for the variation of fundamental constants [21] would benefit from measuring relative x-ray frequency shifts of states in HCIs [22], testing a potential drift of the fine-structure constant α.

Here, we introduce a mechanism to realize frequency combs at x-ray FEL sources that define relative frequency standards locked to an atomic (or ionic) reference transition. We would like to emphasize that the thus-created comb structure will not be stabilized on an absolute frequency scale, as it is currently possible with octave-spanning optical or HHG-based frequency combs, including a stable carrier–envelope offset frequency ${{f}_{{\rm ceo}}}$. However, referencing to an atomic resonance as proposed here allows for precisely measuring frequency differences $\Delta f$. As we show below, $\Delta f$ can be locked to precisely measured radio/microwave frequencies ${{f}_{{\rm rep}}}$, which is the repetition rate of an optical comb, without the need to define an absolute frequency marker with stable ${{f}_{{\rm ceo}}}$, nor requiring octave-spanning spectra. As demonstrated in [23], where optical frequency ratios (${{f}_{1}}/{{f}_{2}}$) are precisely measured and compared for setting a constraint on the variation of α, we expect that precisely measured frequency differences ($\Delta f={{f}_{1}}-{{f}_{2}}$), e.g. across different species of highly charged ions, directly accessed in the x-ray domain, will provide a complementary and extremely sensitive [22, 24] approach to this endeavor, and will enable the toolbox of frequency metrology to be utilized at x-ray energies. The key idea is conceptually related to sideband generation of continuous-wave (cw) lasers via classical electro-optical modulation [25–29], dating back to the early roots of frequency combs [11, 12, 30]. The classical phase modulation is replaced by a quantum-mechanical phase modulation of excited states of atoms, and the cw laser is replaced by a coherently excited resonance in any kind of matter (e.g. atoms, ions, Móssbauer nuclei, etc.). By locking to an atomic reference transition at a high (x-ray) photon energy, instead of zero frequency as is now possible for optical combs, absolute frequencies are not immediately accessible. However, relative frequency metrology at high precision opens up in the x-ray domain. It allows for comparing nearby x-ray transitions in HCIs as required for the examples of $\dot{\alpha }$ searches and isotope-shift measurements. A first scheme of how the x-ray domain can be accessed with frequency combs was discussed in [31], however it required anarrow-band intense x-ray source which is not available to date. In the mechanism presented here, we enable the generation of frequency combs that are referenced to high-frequency atomic transitions, using currently-available pulsed x-ray light at FELs. Here, the intrinsic natural line width and transition frequency of an atomic resonance defines the resolution and position of the generated comb. Utilizing the results of the time-domain manipulation of spectral line shapes [32], we demonstrate below how such frequency combs can be generated, solely by the interaction of available light pulses of duration shorter than the resonance lifetime.

The interaction of light with matter can be described via the dipole-response function which is directly proportional to the systemʼs polarizability. For a dilute medium, the imaginary part of this complex-valued function describes absorption or gain of transmitted electromagnetic radiation (see [33, 34] for reviews). For a two-level system, i.e. an isolated resonance, the time-dependent dipole response d(t) after delta-function-like excitation at time t = 0 is given by

$$\begin{eqnarray}&&d(t)\propto i{{e}^{-i{{E}_{{\rm r}}}t}}{{e}^{-\frac{\Gamma }{2}t}}\theta (t),\end{eqnarray} \tag{ 1 }$$

where ${{E}_{{\rm r}}}$ and Γ denote the energy and the decay width of the excited state, respectively, and $\theta (t)$ is the Heaviside function. Atomic units (a.u.) are used throughout. Through the Fourier transform, the time-dependent dipole response d(t) is related to the frequency-dependent response $\tilde{d}(E)$, $\tilde{d}(E)=\int _{-\infty }^{+\infty }d(t){{e}^{+iEt}}\;{\rm d}t$. Computing the imaginary part of the Fourier transform of equation (1)

$$\begin{eqnarray}&&{\rm Im}\left\{ \tilde{d}(E) \right\}\propto {\rm Im}\left\{ i\frac{1}{\Gamma /2-i\Delta E} \right\}\end{eqnarray} \tag{ 2 }$$

yields the well-known Lorentzian line shape, where $\Delta E=E-{{E}_{{\rm r}}}$ is the energy detuning from the resonance. The decay width Γ determines the full width at half maximum (FWHM) of the spectral response.

A phase-control mechanism was demonstrated in [32], in which it was shown how Lorentzian and Fano line shapes can be transformed into each other. This is easily understood by multiplying a phase factor ${{e}^{i\phi }}$ to d(t) in equation (1), or to the argument $\tilde{d}(E)$ of the imaginary part in equation (2). Experimentally, this is realized by short-pulsed (delta-like) excitation and phase manipulation of the dipole response, which subsequently decays over a much longer time scale, i.e. its natural life time $\tau =1/\Gamma$. In general, any phase change $\Delta \phi$ can be realized via impulsive energy shifts $\delta {{E}_{{\rm r}}}(t)$ and is given by

$$\begin{eqnarray}&&\Delta \phi =\int \delta {{E}_{{\rm r}}}(t){\rm d}t,\end{eqnarray} \tag{ 3 }$$

where the integral is to be taken over the duration of the interaction, shifting the energy of the state (e.g. by using a strong laser pulse). Here we extend this control concept to periodic phase manipulations which cover the whole time of coherence decay of the two-level system.

Figure 1(a) shows the temporal response of the two-level system after delta-like excitation at t = 0. Incremental phase steps $\Delta \phi$ are inserted periodically every integer multiple of ${{T}_{{\rm rep}}}$, after starting with an initial phase of ϕ. Via the Fourier transform, the spectral response is revealed: a frequency comb is generated which can be given as an analytical expression without any approximation:

$$\begin{eqnarray}&&{\rm Im}\left\{ \tilde{d}(E) \right\}\propto {\rm Im}\left\{ i{{e}^{i\left( \phi -\Delta \phi /2 \right)}}\;\times \right.\left. \mathop{\sum }\limits_{n=-\infty }^{+\infty }\frac{{{a}_{n}}}{\Gamma /2-i\left[ \Delta E-2\pi \cdot {{f}_{{\rm rep}}}\left( n-\Delta \phi /2\pi \right) \right]} \right\},\end{eqnarray} \tag{ 4 }$$

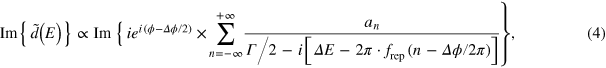
with comb-teeth coefficients

$$\begin{eqnarray}&&{{a}_{n}}=-\frac{{\rm sin} (\Delta \phi /2)}{\pi (n-\Delta \phi /2\pi )},\end{eqnarray} \tag{ 5 }$$

where n is an integer number, and ${{f}_{{\rm rep}}}=1/{{T}_{{\rm rep}}}$ is the repetition frequency of the applied phase steps $\Delta \phi$. The line shape of each comb tooth is Lorentzian, provided that $\phi =\Delta \phi /2$ as explained below. Equation (4) thus reveals the typical spectral response of a frequency comb spanning across the resonance energy and spaced by integer multiples of the repetition frequency. An illustration of this spectral response is shown in figure 1(b). Comparing equation (4) with equation (2), each comb tooth has equal width Γ and a common phase factor ${{e}^{i(\phi -\Delta \phi /2)}}$, leading to equal line shapes of the comb teeth as set by the global offset phase ϕ. The strength of each tooth is given by a_n in equation (5). As shown in figure 1(b), symmetric Lorentzian comb teeth are located on each side of the resonance frequency, separated by ${{f}_{{\rm rep}}}$. With parameters set to $\phi =\frac{1}{2}\pi$ and $\Delta \phi =\pi$, the comb at positive energies $\Delta E\gt 0$ appears with negative amplitudes (gain), while it appears with positive amplitudes (absorption) at negative energies $\Delta E\lt 0$. Setting the parameters to $\phi =\frac{3}{2}\pi$ and $\Delta \phi =\pi$, the structure of the created frequency comb is conserved except that the absorption and gain sides exchange their roles. The common Lorentzian absorption line shape as described by equation (2) is also recovered in equation (4). If ϕ is set to 0 or π, while keeping $\Delta \phi =0$, a positive (absorption) or negative(gain) Lorentzian line shape results. For the general case $\Delta \phi \ne 0$, comparing with equation (2), the offset phase ϕ should be set to $\phi =\Delta \phi /2$, or $\phi =\pi +\Delta \phi /2$ in order to keep the Lorentzian symmetric line shape for each comb tooth. Investigating the influence of Gaussian noise $\Delta {{\phi }_{{\rm rms}}}$ on the sequential phase steps, the frequency definition (width) of the comb teeth is slightly broadened, approximately quantified by

$$\begin{eqnarray}&&{{\Gamma }_{{\rm total}}}=\Gamma \sqrt{1+0.49{{\left( \frac{\Delta {{\phi }_{{\rm rms}}}}{2\pi } \right)}^{2}}\frac{2\pi {{f}_{{\rm rep}}}}{\Gamma }}\end{eqnarray} \tag{ 6 }$$

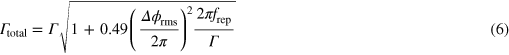
for values $\Delta {{\phi }_{{\rm rms}}}/(2\pi )\leqslant 3\%$ and $2\pi {{f}_{{\rm rep}}}/\Gamma \leqslant 85$.

Zoom In Zoom Out Reset image size

So far, we restricted our discussion to the 'maximum' phase steps $\Delta \phi =\pi$. According to equation (4), another important feature of the impulsive phase-shift method is found: the location of the frequency comb can be tuned by setting the incremental phase step $\Delta \phi$ as illustrated in figure 2. The location of the n-th comb tooth is given by

$$\begin{eqnarray}&&{{E}_{n}}={{E}_{{\rm r}}}+n\times 2\pi {{f}_{{\rm rep}}}-{{f}_{{\rm rep}}}\times \Delta \phi ,\end{eqnarray} \tag{ 7 }$$

having a symmetric Lorentzian shape with appropriate choice of the initial offset phase (e.g. $\phi =\Delta \phi /2$). Equation (7) compares to the standard definition of optical frequency combs, at frequencies spaced by integer multiples of the repetition rate. In our case, the comb is referenced not to zero frequency, but to the modulated transition at energy ${{E}_{{\rm r}}}$. Beating the generated comb with the original transition frequency provides the feedback signal for stabilizing $\Delta \phi /2\pi$ to a rational fraction of ${{f}_{{\rm rep}}}$, as described for the experimental implementation below. The magnitude of the respective comb teeth is also changed as a function of $\Delta \phi$, determined by the coefficients a_n as given by equation (5). Deviating from the 'maximum' phase step $\Delta \phi =\pi$ will lead to a decrease of the comb-tooth amplitude. For the case of $\Delta \phi =\pi$, 30 comb teeth are produced on each side of the resonance energy ${{E}_{{\rm r}}}$ above the threshold of 1% of the original resonance strength, while 3000 comb teeth are generated on each side above the threshold of 0.01% of the original resonance strength. In the more general case of $\Delta \phi \ne \pi$, the number of comb teeth above a given threshold is reduced by the factor ${\rm sin} (\Delta \phi /2)$.

Zoom In Zoom Out Reset image size

With the thus-far presented formulas (equations (4) and (5)), we assumed instantaneous phase shifts $\Delta \phi$ within zero time. To approach realistic situations, in the following we extend our model to finite-duration phase shifts. We assume a linear change of the phase step as illustrated in figure 3(a), where the duration w of linear variation is normalized to the repetition period ${{T}_{{\rm rep}}}$. The spectral response of such a system is again given by equation (4), but now with a different coefficient

$$\begin{eqnarray}&&{{a}_{n}}=-\frac{\Delta \phi \;{\rm sinc}\left\{ \pi \left[ \left( n-\Delta \phi /2\pi \right)w+\Delta \phi /2\pi \right] \right\}}{2\pi (n-\Delta \phi /2\pi )},\end{eqnarray} \tag{ 8 }$$

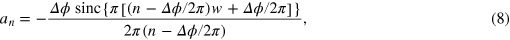
which reduces to equation (5) for w = 0. Thus, the regularity of the frequency comb is preserved, except the amplitudes of the comb teeth are now described by equation (8). Setting w = 0.05, frequency combs obtained with positive and negative phase steps are shown in figures 3(b) and (c), where the coefficients a_n as given in equation (8) are shown as envelope functions. Interestingly, the magnitude of the comb teeth is enhanced on the positive ($\Delta E\gt 0$) and negative ($\Delta E\lt 0$) energy side, respectively (see figures 3(b) and (c)), while the 'center of gravity' is shifted into this direction. Note that the direction of the comb teeth (gain/absorption) can still be set by using the offset phase ϕ as discussed above. For different rise times w the envelope function of the comb teeth as given by equation (8) is plotted in figure 3(d). A slight enhancement of selected magnitudes even compared to the 'ideal' zero-width case (w = 0) is observed.

Zoom In Zoom Out Reset image size

After the general introduction of the phase modulation of the dipole response for frequency comb generation, we suggest the first realistic experimental implementation. Here we present theoretical results for the $1{{{\rm s}}^{2}}-1{\rm s}\;2{\rm p}$ transition in helium or helium-like beryllium in the XUV and soft x-ray region of the electromagnetic spectrum. Their natural lifetimes are calculated to ∼ $6\;{\rm ns}$ (He) and ∼ $8\;{\rm ps}$ (Be²⁺). Employing femtosecond-pulsed XUV or soft x-ray radiation from an FEL, the excitation of the resonances can thus be described as delta-like, as required for the phase-modulated response function which we introduced above.

After the excitation, short laser pulses (also in the fs regime) can be utilized to periodically modify the spontaneous decay of the excited $1{\rm s}\;2{\rm p}$ level. This external laser electric field induces periodic AC Stark shifts $\delta {{E}_{{\rm r}}}(t)$ on the energy of the excited level ${{E}_{{\rm r}}}$ which are due to the dipole coupling to nearby off-resonant levels such as $1{\rm s}\;2{\rm s}$, $1{\rm s}\;3{\rm s}$, and $1{\rm s}\;3{\rm d}$. The atomic dipole response $d(t)$ and its Fourier transform $\tilde{d}(E)$ are obtained with the solution of the master equation [35, 36] which describes the atomic dynamics in the presence of the periodic train of femtosecond pulses in figure 4(a). The transition energies are taken from [37], whereas decay rates and dipole matrix elements are computed with grasp2K [38]. The laser field is described classically by the function

$$\begin{eqnarray}&&\mathcal{E}(t)={\rm cos} ({{\omega }_{{\rm L}}}t)\mathop{\sum }\limits_{j=0}^{\infty }\tilde{\mathcal{E}}(t-{{t}_{0}}-j{{T}_{{\rm rep}}}),\end{eqnarray} \tag{ 9 }$$

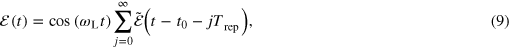
where t₀ is the central time of the first pulse, ${{\omega }_{{\rm L}}}$ is the central frequency, and $\tilde{\mathcal{E}}(t)={{\tilde{\mathcal{E}}}_{0}}{\rm sech}(\gamma t)$ is the single-pulse envelope [39, 40]. Here, the field-strength maximum ${{\tilde{\mathcal{E}}}_{0}}$ is associated with the peak intensity $I=c\tilde{\mathcal{E}}_{0}^{2}/8\pi$, and the bandwidth γ is related to the FWHM pulse duration $T=2\;{\rm arccosh}\;(\sqrt{2})/\gamma$ of $|\tilde{\mathcal{E}}(t){{|}^{2}}$. We assume near-infrared (NIR) femtosecond laser pulses centered on $1.5\;{\rm eV}$ with 100-fs (FWHM) duration. Each pulse causes a phase shift as shown by equation (3), which displays an approximately linear increase with the laser peak intensity, $\Delta \phi \approx -(1/2){{\alpha }_{d}}\int {{\tilde{\mathcal{E}}}^{2}}(t)dt$, with the effective dynamic polarizability α_d of the $1{\rm s}\;2{\rm p}$ level. The values extracted from our calculations, ${{\alpha }_{d}}=354\;{\rm a}.{\rm u}.$ for He and ${{\alpha }_{d}}=-25.7\;{\rm a}.{\rm u}.$ for ${\rm B}{{{\rm e}}^{2+}}$, are in good agreement with dynamic polarizabilities calculated for weak constant-amplitude fields [41–43]³ . This implies that a phase shift equal to $|\Delta \phi |=\pi$ is obtained by tuning the peak intensity of the train of pulses to $1.37\times {{10}^{11}}\;{\rm W}\;{\rm c}{{{\rm m}}^{-2}}$ and $1.87\times {{10}^{12}}\;{\rm W}\;{\rm c}{{{\rm m}}^{-2}}$, in the case of He and ${\rm B}{{{\rm e}}^{2+}}$, respectively.

Zoom In Zoom Out Reset image size

The time delay τ between the delta-like excitation and the NIR pulse train holds the key to independently modifying the initial (offset) phase ϕ: it can be set such that the first NIR pulse only partially overlaps with the excitation, thus the phase shift caused by the first NIR pulse (i.e. the offset phase) is controlled independently, here tuned to $\phi =\pi /2$. The resulting spectral response of this scheme is shown in figures 4(b) and (c), where the repetition frequency ${{f}_{{\rm rep}}}$ of the NIR pulse train is tuned to 10 GHz for He, and to 100 GHz for Be²⁺ in order to separate the individual comb teeth. Its beat signal with the original transition frequency can be locked to ${{f}_{{\rm rep}}}$ [see also the discussion of equation (7) above] by using, for example, acousto-optical modulators to close the feedback loop that controls the shot-to-shot NIR pulse intensity and thus the phase shift $\Delta \phi$. The spectral response of the three-level model shown in figures 4(b) and (c) agrees excellently with our previously developed analytical formalism as shown in figure 1(b). Both the intensity and repetition rate of the NIR pulses are higher in magnitude than readily available laser pulses which can be coupled out of a mode-locked oscillator. For a first demonstration of the concept, therefore, we propose to take advantage of amplified Ti:Sa laser pulses coupled into external Fabry–Perot cavities which should easily provide the assumed specifications. In the near future, we expect our method to take advantage of ongoing active research in the direction of high-power multi-GHz femtosecond oscillators [43–45], thus creating another fundamental physics motivation for the development of such ultrafast laser technology.

In conclusion, frequency combs locked to atomic resonances can be generated by a quantum phase modulation method. The two presented examples demonstrate the experimental feasibility of the process in the XUV and soft x-ray domain. The method itself however can in principle be transferred to any spectral region, including the hard x-ray domain by using transitions in HCIs [18], where metastable states [46] will be desirable targets to enhance the combʼs frequency precision. The analytical expressions presented in this work can be readily used to estimate the exact experimental parameters required for the specific system of interest. In all generality the formalism developed herein is just one example of the potential provided by arbitrary tailoring of spectral line shapes via direct temporal access to the response function. The generalization of this approach should thus not only enable high-precision metrology and related applications at extremely high frequencies, but also pave the way for pulse shaping at arbitrary frequencies.

We thank Thomas Allison, Itan Barmes and José R Crespo López-Urrutia for a critical reading of the manuscript and providing very helpful comments. The authors acknowledge support from the Max Planck Research Group program and the DFG (grant PF790/1-1). Z Liu acknowledges the scholarship award for excellent doctoral students granted by the Ministry of Education of China.