Abstract
The coupling effects of subwavelength high-permittivity (εr > 100) arrayed ceramics which exhibit magnetic and electric Mie resonances are investigated by electromagnetic full-wave analysis. Special attention was paid to the symmetry properties of both magnetic- and electric-induced dipoles by varying independently the array periodicity. In agreement with the interactions between electric and magnetic dipoles, it is shown that resonance frequency shifts toward lower (higher) frequencies can be obtained, which depends on the longitudinal (transverse) dipole coupling strengths. Moreover, the emergence of quasi-bound states between tightly coupled basic cells is pointed out for the electric Mie resonances, which shows an unexpected frequency shift with a reverse variation.
Export citation and abstract BibTeX RIS
GENERAL SCIENTIFIC SUMMARY Introduction and background. The coupling effect between atoms is of prime importance for the optical spectroscopy of common materials. In recent years, electromagnetic metamaterials, which are artificial structures composed of subwavelength periodic arrayed elements, have attracted much attention owing to their singular properties, such as negative/zero index, which cannot be found in natural materials. These unusual properties result directly from the electric/magnetic resonances of basic elements, which can be considered 'meta-atoms'. Inspired by natural atom interplay, it is of great interest to have a deeper understanding of meta-atom coupling effects and the underlying physics.
Main results. In this paper, the coupling effects of subwavelength high-permittivity (εr > 100) arrayed ceramics which exhibit magnetic and electric Mie-resonances are investigated by electromagnetic full-wave analysis. Special attention is paid to the symmetry properties of both magnetic- and electric-induced dipoles by varying the array periodicity independently. In agreement with the interactions between electric and magnetic dipoles, it is shown that the resonance frequency shifts towards lower (higher) frequencies can be obtained, depending on the longitudinal (transverse) dipole coupling strength. Moreover, the emergence of quasi-bound states between tightly coupled basic cells is indicated for those electric Mie resonances that show an unexpected frequency shift with a reverse variation.
Wider implications. It is believed that this study of coupling effects will reveal new degrees of freedom with respect to the conventional design rules focused on the basic cell, notably targeting negative index media.
 Figure. Local electric field for electric Mie resonance distorted as the periodicity along the H-field decreases.
Figure. Local electric field for electric Mie resonance distorted as the periodicity along the H-field decreases.
1. Introduction
Artificial magnetism using nonmagnetic conductors is currently attracting much attention with the possibility of fabricating negative permeability media on the basis of current loop resonance effects induced by the incident magnetic field. So far, split ring resonators (SRRs) arrays have been widely used over a large fraction of the electromagnetic (EM) spectrum [1–6]. Basically, this kind of resonator is planar and thus shows anisotropic EM responses. Such an anisotropy can be problematic for many practical applications, notably for all-angle scattering since a proper polarization of the magnetic field, normal to the SRR plane, is required. From the technological point of view, the anisotropy problem can be alleviated by quite complex techniques, notably in the optical spectral range such as the SRR patterning on the various faces of a dielectric cube [5, 6]. A simpler solution is to take advantage of the so-called Mie resonance in high-permittivity (κ) dielectrics. Notably, this possibility was considered theoretically [7–13] and assessed experimentally by employing various kinds of dielectrics and resonators [16–25]. A very high value of the relative dielectric constant localizes the EM wave on a scale much shorter than the wavelength in free space, and various resonance orders, which correspond either to an electric dipole or to an artificial magnetic polarization, can be pointed out. Recently, we showed that barium strontium titanate (BST) ceramics can be used as high-κ dielectrics [20–23]. On this material basis, various Mie-type resonance modes are evidenced from the frequency dependence of the transmittance and reflectance of multilayered ceramics arrays with the subsequent retrieval of effective parameters. An artificial magnetization can be assessed by the mapping of the electric field vector owing to unambiguously circular displacement currents (J ∼ ∂E/∂t) whose direction depends on the s- or p-polarization of the magnetic field. A Lorentz-type frequency dependence can be determined for the effective permeability or permittivity dispersion characteristic whose frequency response is phase-shifted by π above the Mie-type magnetic or electric resonance.
Until now, investigations of Mie resonances have mainly concentrated on the underlying physics of isolated cells by satisfying the homogeneity criterion, namely the fact that the relevant dimensions are much shorter than the wavelength of the impinging EM waves. Owing to the extremely high permittivity values, strong localization of the EM modes is achieved in the close vicinity of the high-κ particles with ultra-short-scale evanescence tails. Under this condition, the coupling effects between adjacent cells are rarely considered, although the interactions between metamaterial particles could play an important role in the achievement of singular properties. For instance, Lai et al [24] reported negative index behavior by using the single-zirconia resonator with a combination of displacement current and Mie resonance [24]. Wheeler et al [9] investigated the coupling effect by restricting their analysis to the interaction on the magnetic dipole of dielectric particle clusters [25].
In this context, special attention will be given here to the interactions between neighboring densely arrayed high-κ ceramics governed by the Mie-type magnetic and electric resonance effects. Toward this goal, the impact of the periodicity of arrayed ferroelectric cubes with attainable complex permittivity values on the magnetic and electric resonance frequencies was investigated numerically by full-wave analysis. It is shown that the odd or even symmetry conditions of induced dipoles have a significant effect on the frequency and magnitude of the magnetic and electric Mie resonances. Transverse or longitudinal dipole coupling is here discriminated by independent variations of the array period along the three directions of space. As expected from dipole–dipole coupling theory, it is shown that opposite frequency shifts are achieved for the ground magnetic state, which shifts toward higher frequency (blueshift) for a parallel dipole scheme and the electric response toward lower frequency (redshift) with an end to end arrangement. In addition, an unexpected quasi-bound state between tightly coupled cells was also pointed out for the electric resonance yielding a reverse frequency variation with respect to the aforementioned rules.
The paper is organized as follows. In section 2, we calculate the eigenmodes for a Mie resonance-based ferroelectric cube array. Section 3 will be devoted to the influence of independent changes in the periodicity in the three main directions of space on the transmission spectra, which are interpreted in terms of magnetic and electric dipole interactions. Finally, concluding remarks and prospects are reported in section 4.
2. Electromagnetic behavior of the elementary cell
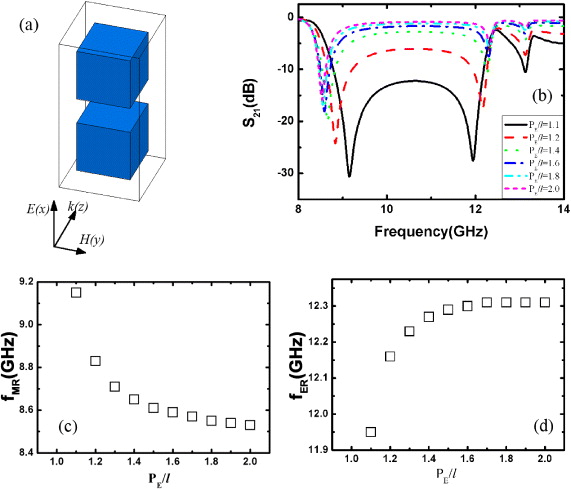
The unit cell of dielectric metamaterial used here is composed of a single BST ceramic cube surrounded by air (in practice this can be a porous medium like a foam whose relative permittivity is close to unity). We assumed here the use of BST ceramics with a complex relative permittivity ε = 200 + 2j, which is readily attainable and thus realistic notably with respect to the assumed value of loss tangent in the current ferroelectrics technology [26]. The first stage was to study the scattering response of a single layer (in the propagation direction) of ferroelectric cubes with a side length l of 2 mm arrayed in the transverse directions. Plane wave is assumed for the EM field incidence with polarization conditions, as shown in figure 1(a), which correspond to the electric field direction along the x-axis and to the magnetic field direction along the y-axis, respectively. Basically, the full-wave analysis was carried out for the complex scattering parameters (transmittance and reflectance) calculation by means of a commercial finite integration time domain package, CST Microwave Studio. Figure 1(b) presents the scattering parameters for the single layer composed of BST cubes stacked with equal periodicity along transverse directions. From this figure, it can be noted that three transmission dips occur at 8.44, 12.14 and 13.0 GHz, respectively. In this paper, we will concentrate on the first two minima of transmission owing to the fact that the resonance strength of the third one is much weaker compared with that of the previous resonance modes.
Figure 1. (a) Schematic diagram of the elementary unit cell for dielectric metamaterial. (b) The frequency dependence of the magnitude of scattering parameters of single-layer dielectric metamaterial. The side length of the BST cube l = 2.0 mm, while the periodicities along the E, H and the thickness of the dielectric metamaterial layer are kept constant as 2.5 mm. The cube has a relative permittivity of 200 + 2j.
Download figure:
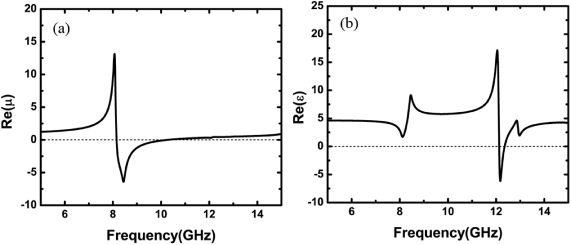
Standard imageIn order to determine the resonance modes, the dispersion of effective EM parameters was extracted from the frequency dependence of the scattering parameters by using a well-developed retrieval algorithm [27–29]. As shown in figure 2, the BST cube array exhibits a Lorentz-type dispersion for the effective permeability with negative values between the magnetic resonant frequency, fMR = 8.44 GHz, and the magnetic plasma frequency, fMP = 9.8 GHz. A concurrent anti-resonance state of the effective permittivity is due to the periodicity effect [30]. The strongest resonance effect of the effective permittivity occurs slightly above 12 GHz around which negative values are achieved for frequencies ranging from the electric resonance frequency, fER = 12.14 GHz, up to the electric plasma frequency, fEp = 12.3 GHz. As a general rule, the depth of the dip in transmission is stronger for the magnetic response.
Figure 2. Frequency dependence of the real parts of effective permeability (a) and permittivity (b).
Download figure:
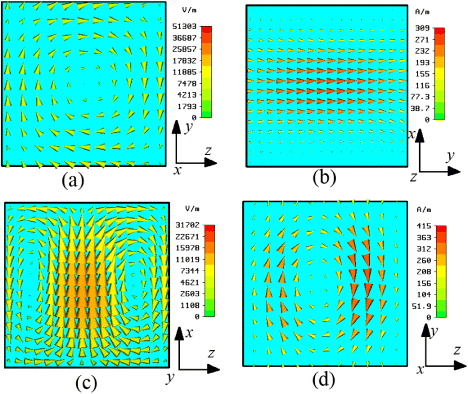
Standard imageThe maps of the electric and magnetic fields at the aforementioned resonant frequencies (fMR = 8.44 GHz and fER = 12.14 GHz) are displayed in the center of the cubes. At fMR = 8.44 GHz, the electric field in the xz-plane (figure 3(a)) shows a typical gallery mode, whereas the magnetic field plotted for the same frequency in the xy-plane shows localization in the center of the cube. These field patterns support the interpretation of current loops induced by the external magnetic field yielding a magnetic response shifted by π above the magnetic resonance frequency,fMR. For the second Mie resonance at 12.14 GHz, linearly polarized displacement currents are excited with a resonant pattern similar to electric dipole characteristic (figure 3(c)). Concomitantly, the magnetic field map reported in figure 3(d) in the yz-plane shows a wrapping pattern supporting the interpretation of an electric dipole-related resonance. On the basis of this analysis of the EM response of a cube array with the identification of the magnetic and electric Mie-type resonances, we are now considering in the next section various coupling schemes by varying independently the spacing between BST cubes along different lattice directions.
Figure 3. Local electric field (a, c) and magnetic field (b, d) around the first and second resonance frequencies.
Download figure:
Standard image3. Periodicity influences
To investigate the mutual coupling between adjacent BST cells along various Cartesian coordinate axes, we modified separately the periodicities along the three main axes, i.e. periodicity along the external electric field, PE, the magnetic field, PH, and the propagation direction, Pk. For instance, to investigate the periodicity influence along the electric field direction, we gradually varied PE from 4.0 to 2.2 mm while the other two lattice periodicities PH and Pk were kept constant as 3.0 mm.
3.1. Influence of periodicity along the E-field (PE) direction
Figure 4(b) shows the calculated transmission spectra of dielectric metamaterial versus the ratio of PE and l. From figure 4(b), it can be noted that the magnetic and electric transmission dips become more pronounced and exhibit an opposite frequency shift with decreasing PE/l. The enhancement in the rejection can be interpreted by an increase of the filling factor. On the other hand, one can expect opposite shifts of the resonant frequencies, toward higher frequencies for the magnetic resonance and lower frequencies for the electric resonance with decreasing PE/l as demonstrated in figures 4(c) and (d), showing the variation of transmission minima for magnetic and electric coupling effects. For the magnetic resonance as PE/l varies from 1.1 to 2.0, the magnetic resonance frequency shifts from 9.15 to 8.53 GHz and it also indicates a saturation of the coupling effect for magnetic resonance when there is a twofold increase of the lattice spacing with respect to the side length of the resonator along the x direction. In contrast, the electric resonance frequency decreases from 12.34 GHz down to 11.95 GHz with a variation by 400 MHz. The electric resonance frequency saturates around PE/l = 1.7, hence showing less coupling sensitivity in comparison with the magnetic resonance.
Figure 4. (a) Schematic view of a BST cubes array stacked with varying periodicity along the E(x) direction. (b) Transmission spectra for various PE/l. The periodicities along the other two directions are kept constant (PH and Pk = 3.0 mm.). Frequency dependence of (c) magnetic resonance fMR and (d) electric resonance fER as a function of PE/l.
Download figure:
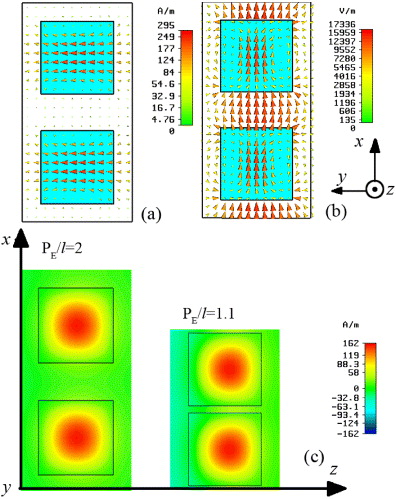
Standard imageTo give an insight into the underlying physics responsible for the contrary frequency dependence of magnetic and electric resonance with respect to PE, we plot in figure 5 the local electric and magnetic fields at the corresponding resonance frequencies. Around the magnetic resonance frequency, neighboring magnetic dipoles induced by the circular displacement currents are aligned parallel to each other, indicating that the interplay effect is dominated by the repulsive force between the transverse magnetic dipoles, as shown in figure 5(a). This repulsive-type coupling at near field explains the increase of the resonant magnetic frequency when the high-permittivity cubes are in close proximity and the saturation of the frequency shift when they are well separated. In contrast, for the electric resonance occurring at about 12.2 GHz, it is seen from the electric field map that the electric dipoles are polarized in an 'end-to-end' state. The positive ends of each electric dipole are attracted by the negative ones of neighboring electric dipoles and vice versa, giving rise to longitudinal coupling effects, which directly lower the resonance frequency with respect to the original state without any coupling [31, 32]. Evidently, increasing PE/l relaxes the longitudinal coupling effect, hence restoring the resonance frequency of the BST cube to high frequencies. Furthermore, the magnetic resonance frequency shifts by more than 700 MHz, which is much larger than the electric resonance frequency variation with respect to the same change of PE. This can be understood by the fact that the ground magnetic resonance, corresponding to the first Mie resonance, is much stronger with respect to the second Mie (electric-type) resonance, requiring large separation to ignore unit cell interaction.
Figure 5. Magnetic field (a) and electric field (b) maps in the xy-plane induced at 8.6 and 12.27 GHz, respectively. (c) Magnetic field component Hy distribution for the cases with PE/l = 2, 1.1, at the respective magnetic resonance frequencies.
Download figure:
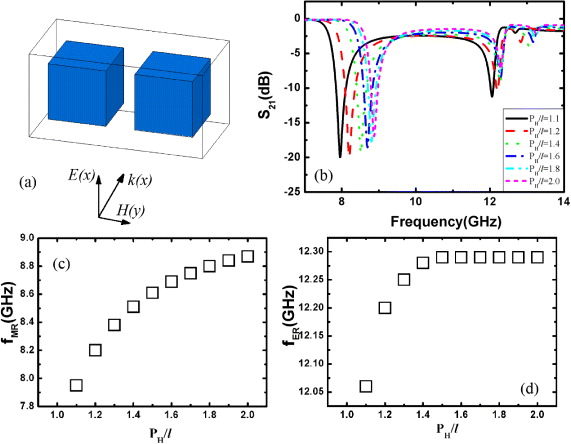
Standard image3.2. Influence of periocity along the H-field (PH) direction
3.2.1. Cube results
In this section, we present the influence of periodicity on the Mie resonances of dielectric metamaterial along the external H(y) direction, PH. Figure 6(b) gives the transmission spectra by varying PH/l from 1.1 to 2.0. In contrast to the resonance frequency variation pointed out in figure 4, the magnetic resonance shifts here toward lower frequency as PH/l decreases. Quantitatively, from figure 6(c), we can find that as PH/l decreases from 2.0 to 1.1, the magnetic resonance, fMR, shifts gradually from 8.87 GHz down to 7.95 GHz with thus a variation by nearly 1.0 GHz. The local field map, shown in figure 7(a), shows that magnetic dipoles localized within the BST cubes are longitudinally polarized, forming an 'end-to-end' coupling and therefore lowering the resonance frequency.
Figure 6. (a) The schematic view of BST cube array stacked along the incident magnetic field direction. (b) Transmission spectra of BST cubes as a function of PH/l. Frequency dependence of (c) magnetic resonance fMR and (d) electric resonance fER for different PH/l.
Download figure:
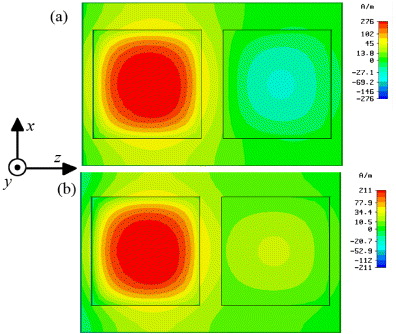
Standard imageFigure 7. Magnetic (a) and electric field maps (b) around the corresponding magnetic and electric resonance frequencies at 8.5 and 12.3 GHz, respectively. BST cube array stacked with periodicity PH = PE = Pk = 3.0 mm. (c) The distribution of local Ex in the yz-plane around the electric resonance frequencies with various PH/l. From top to bottom, the various values of PH/l are 1.5, 1.2 and 1.1.
Download figure:
Standard imageFor the electric resonance, the resonant frequency is almost constant when PH/l decreases from 2.0 down to 1.5, suggesting that the coupling effect can be nearly neglected from the periodicity along the H field. However, we note a similar lower frequency shift for the electric resonance from 12.30 GHz down to 12.05 GHz with a further decrease of PH/l from 1.4 down to 1.1. Although the frequency variation is not remarkable, this result is surprising since such a lower frequency shift implies that a longitudinal coupling between the induced electric dipoles occurs, which is similar to that of the magnetic dipoles. In fact, this is definitely in contrast to the actual local electric field distribution for the case of PH/l = 1.5, as shown in figure 7(b).
For a deeper understanding of this anomaly, figure 7(c) depicts the electric field component Ex for adjacent BST cubes with various lattice spacing: PH/l = 1.5, 1.2 and 1.1. As seen in figure 7(c), for the BST cubes stacked by PH/l = 1.5, the local electric field is concentrated within the center of BST cubes, forming a circular distribution. As neighboring BST cubes approach each other along the H direction, the local electric dipole distributions are distorted gradually from a circular shape to an elliptical form and finally interact with each other, resulting in a 'quasi-bound' resonance mode, yielding the redshift of resonance. This is completely different from the case with magnetic dipole coupling, which is always strongly localized even for tiny lattice spacing, as shown in figure 5(c).
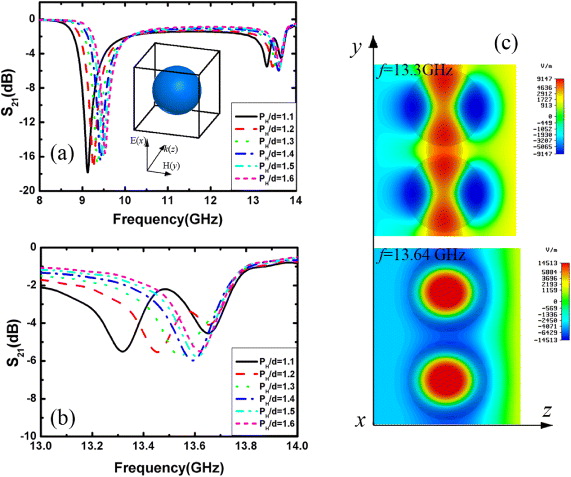
3.2.2. Sphere results
To study the shape influence of the high-permittivity particle, we have further checked the coupling effect between BST spheres, as was considered in [25]. Figure 8(a) gives the transmission spectra of BST spheres versus PH/d (the ratio between periodicity along the H direction and sphere diameter). Besides a similar lower frequency shift of magnetic and electric resonance frequencies with decreasing PH/d, a new transmission dip occurs at the higher frequency range of the electric resonance and close to that of the case with large periodicity, when PH/d becomes smaller than 1.3. These two resonances exhibit opposite shifts with decreasing PH/d, leading to a separation between the two dips. For physical insight, the local electric field patterns were monitored and shown in figure 8(c). It is seen that the induced electric field, around the lower frequency electric resonance, accumulates around the air gap between adjacent spheres, resulting in a 'bound' resonance mode which is more apparent than that of the BST cube (figure 7(c)). On the other hand, the electric field is concentrated inside the sphere for the higher frequency resonance, which is similar to electric resonance of a single sphere, explaining why the higher frequency resonance is located close to the case with large PH.
Figure 8. (a) Transmission spectra of BST spheres versus PH/d. Inset: schematic view of the BST spherical cell. The sphere has a diameter d = 2.2 mm. The periodicities in the other directions are PE = Pk = 3.0 mm. (b) Enlarged view of the electric resonance dependence on varied PH/d. (c) Local electric field component Ex around two electric resonance frequencies: 12.3 GHz (top panel) and 13.64 GHz (bottom panel).
Download figure:
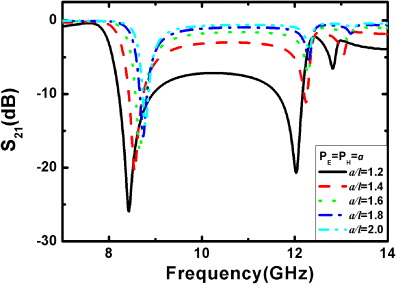
Standard image3.3. Equal transverse spacing PE = PH
From the previous indicative results of antagonist variations, depending on PE and PH, of the Mie resonance of a dielectric cube, it is interesting to consider the case PE = PH. For a single layer of BST cubes along the incident wave direction, as shown in figure 9, decreasing the spacing lattice along the E- and H-field directions simultaneously leads to a lower frequency shift effect on both magnetic and electric resonances. As stated above, the frequency dependence of electric resonance shifts toward lower frequencies because decreasing PE and PH with respect to the cube size l yields the same variation trend of the second Mie resonance. For the magnetic resonance, the lower resonance frequency shift with smaller lattice spacing demonstrates that the longitudinal coupling effect dominates the dipole coupling competition between the respective influences of PE and PH, which is consistent with a larger frequency variation on PH.
Figure 9. The transmission spectra of a single layer of BST cubes versus the ratio of lateral periodicity and side length of BST cube when PE = PH.
Download figure:
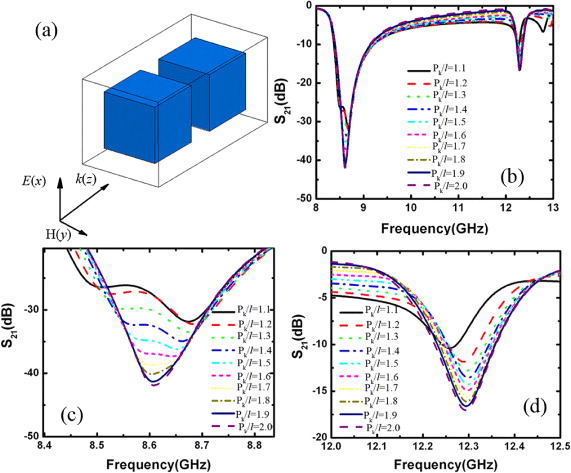
Standard image3.4. Influence of periodicity along the propagation direction (Pk)
The coupling effect occurring between adjacent dielectric cells along the propagation direction was also investigated for a bilayer structure. The main results are reported in figure 10. The numerical results, displayed here, were achieved for the case when the transverse periodicities PE and PH are equal to 3.0 mm, while the spacing between the stacked dielectric cube arrays, Pk, decreases from 4.0 to 2.2 mm. For the large distance with Pk/l = 2.0, two layers of dielectric cell array produce together a single resonance dip either for the magnetic or the electric resonance. However, as the ratio Pk/l decreases from 2.0 to 1.5, the magnetic resonance dip becomes weaker and a new minor dip emerges. For simplicity, we denote the low-frequency and high-frequency dips by fMR1 and fMR2, respectively. By further decreasing Pk, the low-frequency resonance, fMR1, decreases to 8.50 GHz, while the high-frequency resonance, fMR2, increases to 8.65 GHz, showing an opposite trend with respect to Pk/l.
Figure 10. (a) Schematic view of two layers of BST cube array stacked along the incident beam direction. (b) Transmission spectra of BST cubes as a function of Pk/l. Zoomed views of (c) magnetic resonances and (d) electric resonance.
Download figure:
Standard imageA field mapping of the local magnetic field around these two resonance frequencies is plotted in figure 11. Around the low-frequency resonance, fMR1 = 8.5 GHz, the magnetic dipoles inside the two dielectric resonators are induced with an anti-symmetry configuration, resulting in an attractive force between neighboring magnetic dipoles and subsequently lowering the resonance frequency. In contrast, the local magnetic field pattern depicted in figure 11(b) clearly shows that an in-phase oscillation is responsible for the high-frequency resonance, fMR2 = 8.65 GHz.
Figure 11. Local magnetic field induced at (a) fMR1 = 8.50 GHz and (b) fMR2 = 8.65 GHz at the xz-plane. The simulation was performed when PH = PE = 3.0 mm and Pk = 2.4 mm to obtain a visible resonance-splitting phenomena.
Download figure:
Standard imageFor electric resonance, the resonance strength weakens with decreasing Pk, similar to the case of magnetic resonance. However, the resonance frequency is almost independent of the stack spacing for Pk/l > 1.1. Below this threshold, a shift toward lower frequencies is apparent, as seen in the enlarged view of figure 10(d), indicative of the anti-phase oscillation. Unlike the magnetic resonance dependence on Pk, the splitting resonance is not observed for electric resonance of the present simulation model due to the moderate electric resonance strength. During a further investigation, however, we found a similar splitting electric resonance when the electric resonance strength was enhanced by simply increasing the permittivity of the surrounding material (not shown here).
4. Conclusions
In summary, the coupling effects of magnetic and electric resonances for full dielectric metamaterials were investigated numerically via periodicity variations in the three directions of space. It was found that by changing the periodicity along various periodicities, a lower or higher frequency shift of magnetic and electric Mie resonance can be achieved due to the longitudinal or transverse coupling of the induced dipoles. Besides, we have pointed out the existence of a quasi-bound resonant state between tightly coupled unit cells, which is responsible for the unexpected frequency shift of the electric resonance. Full dielectric particles possess the intrinsic advantages of isotropic and low loss EM properties. It is therefore believed that new degrees of freedom to control the resonance state can be achieved in the design and fabrication of dielectric metamaterial including single- and double-negative media and zero- and gradient-index materials, by taking advantage of the interplay among the basic cells of arrayed high-permittivity particles. Finally, the conclusions drawn here are quite general, and a generalization to Mie-resonance-based metamaterials operating in the optical spectrum can be envisaged [33–35] provided that sufficient confinement is achieved on a scale much shorter than the operating wavelength.
Acknowledgments
We gratefully acknowledge financial support from the National Natural Science Foundation of China (grant numbers 61101044, 60978053, 90922025, 51032003, 50921061 and 11002112); the National High Technology Research and Development Program of China (863 Program, grant no. 2012AA030403); project sponsored by Scientific Research Foundation for Returned Overseas Chinese Scholars, State Education Ministry of China; NPU Foundation for Fundamental Research (grant no. NPU-FFR-JC20100243); NPU Aoxiang Star Project; and the Research Fund for the Doctoral Program of Higher Education of China (grant no. 20090002120008).