Abstract
By means of combining the influence of temperature and strain rate, and based on the cooperative Eyring model, a phenomenological formulation for the shape memory effect and temperature memory effect of an amorphous shape memory polymer (SMP) is proposed. The internal stress and stored mechanical energy are correlated to shape/temperature memory behaviours below and above the glass transition temperature. The working mechanism and fundamentals for the chemo-responsive shape memory behaviour in SMPs are further investigated in terms of the activation enthalpy parameter for inductive depression. Simulation using the proposed model is compared with the experimental results reported in the literature. Predictions are also made using the proposed model. This phenomenological framework is expected to provide a powerful tool for investigating the underlying thermomechanics that originate in the movement of cooperative segments and segmental relaxations in SMPs.
Export citation and abstract BibTeX RIS
1. Introduction
Shape memory polymer (SMP) is one type of polymeric stimulus-responsive material. A feature is the shape memory effect (SME), which is the capability of a material to regain its permanent shape by means of releasing stored mechanical energy, but only in the presence of the right environmental stimulus such as heat, water or solvent, light, electricity, magnetic field, etc [1–3]. Hence, an SMP is able to have two stable shapes, although one is permanent and the other is temporary [4–6]. In terms of thermodynamics, SMPs are normally viscoelastic and thus respond to stressing in a time and temperature dependent manner [7, 8]. Therefore, the shape memory behaviour of amorphous SMPs has been studied via thermoviscoelasticity, where the mobility change in polymer chains is represented by the viscosity or relaxation time using rheological elements [9, 10]. Exciting results have been obtained in this field that have revealed the feasibility of reproducing the shape memory behaviour following the Arrhenius rule (including the linear Eyring equation and the non-linear Eyring equation), the Williams–Landel–Ferry (WLF) equation or the Vogel–Fulcher–Tammann rule [11–16]. Good agreement between the theoretical predictions and experimental results for the relaxation behaviour of SMPs has been reported [11, 13, 14, 16].
Up until now, modelling via thermoviscoelasticity has been the mainstream in the characterization and prediction of the shape memory behaviour of amorphous SMPs [7–15]. In these pioneer works, the constitutive relations typically rely on a specific modelling frame. For example, in order to capture the sophisticated thermomechanical and recovery behaviours of SMPs, a generalized Maxwell model with multiple non-equilibrium branches (typically 10–20) was employed [8, 17, 18]. The simulation of this model agrees well with the experimental results. By tracing the evolution in stress and strain in all rheological elements, Yu et al revealed that during the free recovery process in amorphous SMPs, the stresses in the elastic springs provided the driving force. The associated the energy release mechanism was also revealed [18–20]. The findings motivated us to further examine whether shape recovery in SMPs can be simply modelled from the internal (or recovery) stress and stored mechanical energy point of view, where the constitutive relations are independent of the actual framework for modelling, so that the implementation is more straightforward for engineers.
This paper is aimed at establishing a phenomenological formulation from an energy point of view to explain the mechanisms in the shape/temperature memory effect in SMPs. Given the internal stress developed in a SMP, the energy stored in it is formulated. In the subsequent recovery process, the strain energy release rate is scaled with the rate of viscous strain release and shape recovery. The cooperative theory of polymers is employed to capture the internal stress developed under external loading on an amorphous SMP. According to the Eyring transition state theory [21], the fundamental process of yielding consists of the jump of macromolecule segment components, and the mechanical properties of these amorphous polymers are related to the structural relaxation of all segment components. In accordance with the Ree–Eyring theory, the rheological processes involve two activation processes, namely  relaxation and
relaxation and 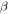 relaxation, referring to a given temperature above or below the glass transition temperature
relaxation, referring to a given temperature above or below the glass transition temperature  respectively [22]. We believe that the Ree–Eyring theory should be apply well to amorphous SMPs, in which the hard component undergoes
respectively [22]. We believe that the Ree–Eyring theory should be apply well to amorphous SMPs, in which the hard component undergoes 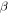 relaxation in the shape recovery process, while the soft ones undergo
relaxation in the shape recovery process, while the soft ones undergo 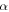 relaxation. The reason is that the shape transition temperature of amorphous SMPs is above and below
relaxation. The reason is that the shape transition temperature of amorphous SMPs is above and below  of soft and hard components, respectively. As is well known, SMPs are normally incorporated with more than two components, one is named the hard component, which retains the configuration and conformation of the macromolecules, while the others are named the soft components, which respond to the applied external stimulus by means of reversible changing in configuration and conformation. Indeed, the viscoelastic and relaxation behaviours of SMPs are a result of the cooperative relaxation of each component.
of soft and hard components, respectively. As is well known, SMPs are normally incorporated with more than two components, one is named the hard component, which retains the configuration and conformation of the macromolecules, while the others are named the soft components, which respond to the applied external stimulus by means of reversible changing in configuration and conformation. Indeed, the viscoelastic and relaxation behaviours of SMPs are a result of the cooperative relaxation of each component.
2. Cooperative model for the multi-SME in amorphous SMPs
Given a piece of pre-deformed amorphous SMP, it is assumed that there exists an internal stress  associated with the stored mechanical energy. In the elastic recovery process, the internal stress works as the driving force. The effective stress
associated with the stored mechanical energy. In the elastic recovery process, the internal stress works as the driving force. The effective stress  is suggested to be given by
is suggested to be given by
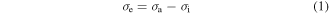
where  is the applied stress. The internal stress is a structural parameter that depicts the arrangement of macromolecule components inherited from the previous thermomechanical history [21, 23, 24]. On the other hand, the amorphous SMP incorporates two or more components, and the flow within the polymer is permitted if all components are moving cooperatively [25]. The cooperative movement of each component involves the occurrence of
is the applied stress. The internal stress is a structural parameter that depicts the arrangement of macromolecule components inherited from the previous thermomechanical history [21, 23, 24]. On the other hand, the amorphous SMP incorporates two or more components, and the flow within the polymer is permitted if all components are moving cooperatively [25]. The cooperative movement of each component involves the occurrence of 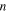 elementary transitions [21, 23], the resulting strain rate
elementary transitions [21, 23], the resulting strain rate  is given by
is given by
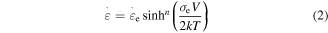
where  is the Boltzmann constant,
is the Boltzmann constant, 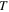 is the temperature,
is the temperature, 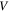 is the activation volume and
is the activation volume and 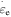 is the characteristic strain rate.
is the characteristic strain rate.  is the number of the segments that need to move cooperatively in the amorphous polymer. For a particular SMP,
is the number of the segments that need to move cooperatively in the amorphous polymer. For a particular SMP, 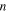 is employed to characterize the cooperative movement of the multiple components. It is a cooperative or superposition constant. Here, the relationship between the yielding stress and internal stress is obtained by incorporating equation (2) into equation (1), which results in
is employed to characterize the cooperative movement of the multiple components. It is a cooperative or superposition constant. Here, the relationship between the yielding stress and internal stress is obtained by incorporating equation (2) into equation (1), which results in
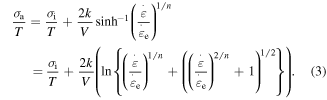
Figure 1 plots the simulated relationship between the effective stress and the strain rate ratio of a polymer. For a given component number, i.e. n = 2, 4, 5, 8 or 10, the effective stress applied on the polymer network gradually increases with the increase in the ratio of strain rate  It is found that the high strain rate ratio results in high applied stress and effective stress at a given internal stress of the polymer. Meanwhile, the simulation also reveals that the internal stress
It is found that the high strain rate ratio results in high applied stress and effective stress at a given internal stress of the polymer. Meanwhile, the simulation also reveals that the internal stress  gradually increases with the increase in the component number
gradually increases with the increase in the component number 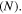 When
When 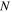 increases from 2, 4, 5, 8 to 10, the effective stress
increases from 2, 4, 5, 8 to 10, the effective stress 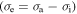 decreases from 1.63 MPa, 1.45 MPa, 1.16 MPa, 1.05 MPa to 1.01 MPa, respectively, at a given strain rate ratio of
decreases from 1.63 MPa, 1.45 MPa, 1.16 MPa, 1.05 MPa to 1.01 MPa, respectively, at a given strain rate ratio of 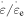 = 6. The internal stress
= 6. The internal stress  of the polymer gradually increases with the increase in the component number of the polymer, as the applied stress is kept as a constant. These results show that a large amount of the internal stress was stored in the polymer transition components.
of the polymer gradually increases with the increase in the component number of the polymer, as the applied stress is kept as a constant. These results show that a large amount of the internal stress was stored in the polymer transition components.
Figure 1. Numerical simulation for the effective stress 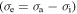 of the SMP with strain rate ratio
of the SMP with strain rate ratio 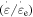 undergoing a given
undergoing a given  (assuming n = N = 2, 4, 5, 8 and 10, where the SMP is incorporated with
(assuming n = N = 2, 4, 5, 8 and 10, where the SMP is incorporated with  components) elementary transitions.
components) elementary transitions.
Download figure:
Standard image High-resolution imageBased on previous works [26–28], the temperature dependence of the internal stress  may be expressed as
may be expressed as
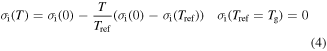
where 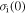 is the internal stress at 0 K.
is the internal stress at 0 K. 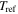 and
and 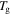 are the reference temperature and glass transition temperature, respectively. A linear dependence of
are the reference temperature and glass transition temperature, respectively. A linear dependence of  on temperature is found as
on temperature is found as
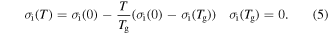
To determine the characteristic strain rate, we follow the Arrhenius law and WLF equation for below and above 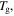 respectively [29], so that
respectively [29], so that
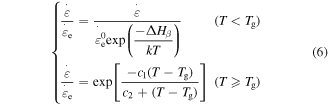
where 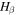 is the
is the  activation energy and
activation energy and 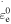 is a constant pre-exponential strain rate that does not depend on temperature.
is a constant pre-exponential strain rate that does not depend on temperature.  and
and 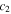 are the WLF parameters. This expression is valid throughout the glass transition with the corresponding expressions for
are the WLF parameters. This expression is valid throughout the glass transition with the corresponding expressions for 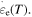 As for the activation enthalpy, for temperatures below
As for the activation enthalpy, for temperatures below  , according to the cooperative model [27],
, according to the cooperative model [27],
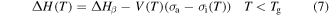
where  is the activation enthalpy and
is the activation enthalpy and  is the activation volume. Since shape recovery in amorphous SMPs at
is the activation volume. Since shape recovery in amorphous SMPs at 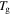 is recognized as an entropy-induced SME, the activation energy is assumed to be
is recognized as an entropy-induced SME, the activation energy is assumed to be 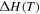 = 0 [30, 31]. Here, it is necessary to discuss the effects of the activation volume on the
= 0 [30, 31]. Here, it is necessary to discuss the effects of the activation volume on the  activation enthalpy.
activation enthalpy.
According to previous works [32–34], it was found that the activation volume is temperature dependent in the thermally activated deformation in glassy polymers. The temperature dependence may be described by [35],
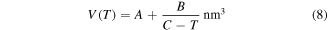
where 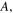
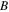 and
and 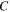 are constants. Here, combination of equations (5), (7) and (8) yields [36, 37]
are constants. Here, combination of equations (5), (7) and (8) yields [36, 37]
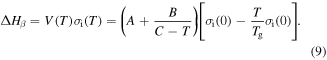
To determine the exact expression for the characteristic strain rate, a natural logarithm formulation is used for the relationship between the strain rate and  activation enthalpy below
activation enthalpy below 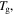 i.e.
i.e.
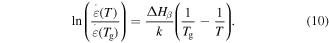
Equation (10) is applicable to one macromolecule. For 1 mol of macromolecules, equation (10) can be rewritten as
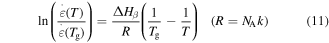
where  is universal gas constant and
is universal gas constant and  is the Avogadro constant. To characterize the shape memory behaviour in SMPs, the Eyring equation and the WLF equation for the relation between relaxation time and strain rate ratio need to be introduced [38]:
is the Avogadro constant. To characterize the shape memory behaviour in SMPs, the Eyring equation and the WLF equation for the relation between relaxation time and strain rate ratio need to be introduced [38]:
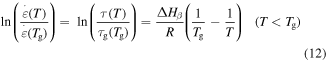
where 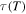 and
and 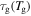 are the relaxation times of the SMP at
are the relaxation times of the SMP at  and
and 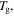 respectively. Combining equations (7), (9) and (12), one has
respectively. Combining equations (7), (9) and (12), one has
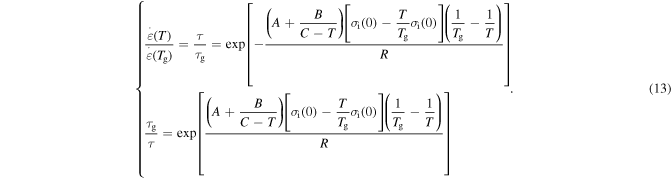
To quantitatively separate the effects of temperature and internal (recovery) stress on the relaxation time of an SMP, it is assumed that 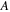 = 0,
= 0, 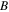 =
=  and
and 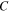 = 1.2
= 1.2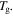
Figure 2 shows the normalized relaxation time versus temperature curves of an SMP, in which the unconstraint shape recovery is driven by internal (recovery) stress. Figures 2(a)–(c) are presented to characterize the effect of temperature on the relaxation time. It is found that the normalized relaxation time 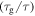 is gradually decreased with the decrease in the temperature
is gradually decreased with the decrease in the temperature 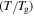 of the polymer, where
of the polymer, where 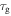 and
and 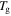 are both constants. These results confirm that the relaxation time
are both constants. These results confirm that the relaxation time 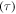 of the SMP is reduced and shortened with the increase in temperature, resulting in accelerated shape recovery. Therefore, it is common to investigate the shape recovery behaviour at relative high temperatures or around
of the SMP is reduced and shortened with the increase in temperature, resulting in accelerated shape recovery. Therefore, it is common to investigate the shape recovery behaviour at relative high temperatures or around 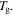 On the other hand, the effect of the internal (recovery) stress on the relaxation time has been studied and the simulation is plotted in figure 2(d). It is revealed that the normalized relaxation time
On the other hand, the effect of the internal (recovery) stress on the relaxation time has been studied and the simulation is plotted in figure 2(d). It is revealed that the normalized relaxation time  is reduced from smooth to sharp with the increase in the internal (recovery) stress
is reduced from smooth to sharp with the increase in the internal (recovery) stress 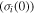 from R, 10R, 100R, 1000R to 10 000R. For a given temperature
from R, 10R, 100R, 1000R to 10 000R. For a given temperature 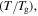 the normalized relaxation time
the normalized relaxation time  is gradually decreased with the increase in the internal (recovery) stress. That is to say, the relaxation time
is gradually decreased with the increase in the internal (recovery) stress. That is to say, the relaxation time 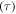 of the SMP becomes large with the increase in the internal (recovery) stress for a given temperature. These results reveal that the internal (recovery) stress plays a critical role in determining the relaxation behaviour of an SMP, and it is released to drive the shape recovery of an SMP upon reaching
of the SMP becomes large with the increase in the internal (recovery) stress for a given temperature. These results reveal that the internal (recovery) stress plays a critical role in determining the relaxation behaviour of an SMP, and it is released to drive the shape recovery of an SMP upon reaching 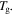
Figure 2. Normalized relaxation time 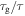 as a function of temperature
as a function of temperature  at a given internal (recovery) stress. (a)
at a given internal (recovery) stress. (a)  = 10R, 20R, 30R, 40R and 50R. (b)
= 10R, 20R, 30R, 40R and 50R. (b) 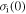 = 100R, 200R, 300R, 400R and 500R. (c)
= 100R, 200R, 300R, 400R and 500R. (c) 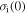 = 1000R, 2000R, 3000R, 4000R and 5000R. (d)
= 1000R, 2000R, 3000R, 4000R and 5000R. (d)  = R, 10R, 100R, 1000R and 10 000R.
= R, 10R, 100R, 1000R and 10 000R.
Download figure:
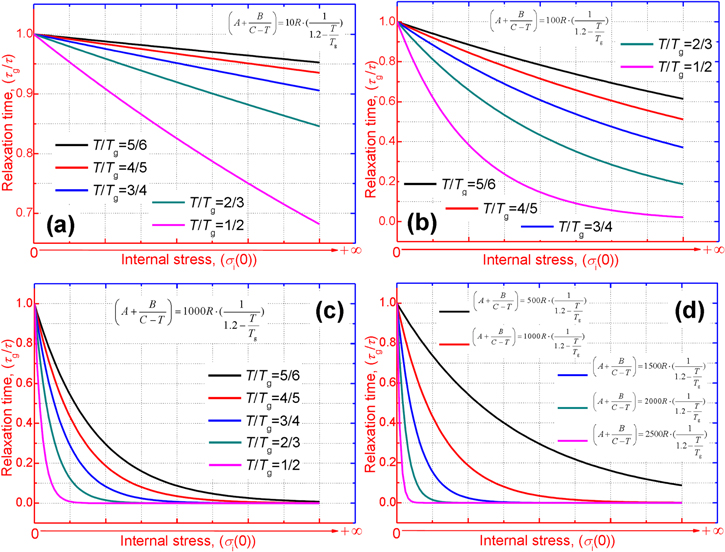
Standard image High-resolution imageFigure 3 shows a number of relaxation curves plotted as the normalized relaxation time versus internal stress at a few different temperatures of  = 5/6, 4/5, 3/4, 2/3 and 1/2. Figures 3(a)–(c) are presented to characterize the effect of internal stress on the relaxation time. It is found that the normalized relaxation time
= 5/6, 4/5, 3/4, 2/3 and 1/2. Figures 3(a)–(c) are presented to characterize the effect of internal stress on the relaxation time. It is found that the normalized relaxation time 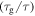 gradually decreases with the increase in the internal stress
gradually decreases with the increase in the internal stress  of the polymer, as
of the polymer, as 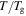 and
and 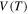 are constants. These results show that the relaxation time
are constants. These results show that the relaxation time 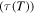 of the SMP is reduced and shortened with the increase in the internal stress, resulting in increased shape recovery speed. It is revealed that high internal (recovery) stress is helpful in enabling faster shape recovery of the SMP.
of the SMP is reduced and shortened with the increase in the internal stress, resulting in increased shape recovery speed. It is revealed that high internal (recovery) stress is helpful in enabling faster shape recovery of the SMP.
Figure 3. Normalized relaxation time  as a function of internal stress for varying temperature (
as a function of internal stress for varying temperature (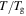 = 5/6, 4/5, 3/4, 2/3 and 1/2). (a)
= 5/6, 4/5, 3/4, 2/3 and 1/2). (a) 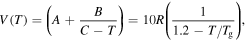 (b)
(b) 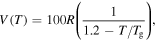 (c)
(c) 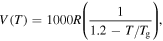 (d)
(d) 

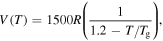
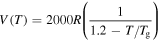 and
and 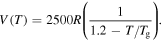
Download figure:
Standard image High-resolution imageOn the other hand, the effect of the activation volume 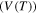 on the relaxation time was studied and the simulation results are plotted in figure 3(d). It is revealed that the curves of the normalized relaxation time
on the relaxation time was studied and the simulation results are plotted in figure 3(d). It is revealed that the curves of the normalized relaxation time 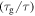 decrease gradually then rapidly with the increase in the activation volume from
decrease gradually then rapidly with the increase in the activation volume from 
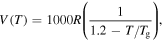
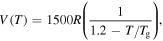
 to
to 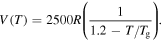 For a given internal stress, the normalized relaxation time
For a given internal stress, the normalized relaxation time 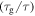 gradually decreases with the increase in the activation volume. That is to say, the relaxation time
gradually decreases with the increase in the activation volume. That is to say, the relaxation time 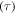 of the SMP becomes larger with the increase in the activation volume for a particular internal stress. These results indicate that an increase in the activation volume increases the relaxation time, and thus more time is required for the SMP to complete its shape recovery.
of the SMP becomes larger with the increase in the activation volume for a particular internal stress. These results indicate that an increase in the activation volume increases the relaxation time, and thus more time is required for the SMP to complete its shape recovery.
3. Cooperative model for the TME in amorphous SMPs
For other types of polymers, the effective stress is important in the characterization of the mechanical performance, where the applied stress always exists. However, the internal stress always plays an essential role in determining the free shape recovery behaviour from the temporary shape back to the permanent shape, as no restriction is applied (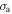 = 0) in the shape recovery process. Therefore, it is necessary to model the internal stress function. Furthermore, it has been found that the temperature memory effect (TME) is also stress dependent [40]. Experimental results have revealed that a higher applied stress is needed for a higher recovery stress in both free and constrained recovery progress. The experimental results and theoretical analyses both imply that there is a strong relationship between the applied stress, internal (recovery) stress and transition temperature in SMPs. Here, a constructive formulation of the stress dependent transition temperature is required to explore the mechanism behind the TME in SMPs.
= 0) in the shape recovery process. Therefore, it is necessary to model the internal stress function. Furthermore, it has been found that the temperature memory effect (TME) is also stress dependent [40]. Experimental results have revealed that a higher applied stress is needed for a higher recovery stress in both free and constrained recovery progress. The experimental results and theoretical analyses both imply that there is a strong relationship between the applied stress, internal (recovery) stress and transition temperature in SMPs. Here, a constructive formulation of the stress dependent transition temperature is required to explore the mechanism behind the TME in SMPs.
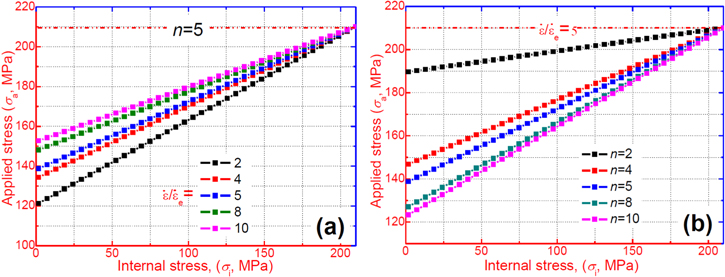
Equation (3) leads to a linear relationship between the applied stress  and internal stress
and internal stress 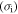 , as shown in figure 4. The internal stress obtained at a higher strain rate ratio is higher than that at a lower strain rate ratio. As the ratio of strain rate
, as shown in figure 4. The internal stress obtained at a higher strain rate ratio is higher than that at a lower strain rate ratio. As the ratio of strain rate  is increased from 2, 4, 5, 8 to 10, the applied stress and internal stress both increase for a given
is increased from 2, 4, 5, 8 to 10, the applied stress and internal stress both increase for a given  elemental transitions, as shown in figure 4(a). The results reveal that the effective stress
elemental transitions, as shown in figure 4(a). The results reveal that the effective stress  is increased with the increase in strain rate ratio. That is to say, the difference between the applied stress and internal stress becomes larger when
is increased with the increase in strain rate ratio. That is to say, the difference between the applied stress and internal stress becomes larger when 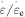 is increased. Meanwhile, as the number of elemental transitions (
is increased. Meanwhile, as the number of elemental transitions (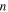 ) is increased from 2, 4, 5, 8 to 10, both the applied stress and internal stress also increase for a strain rate ratio (where
) is increased from 2, 4, 5, 8 to 10, both the applied stress and internal stress also increase for a strain rate ratio (where 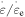 = 5), as shown in figure 4(b). It appears that the effective stress
= 5), as shown in figure 4(b). It appears that the effective stress  decreases with the increase in the elemental transitions. With more elemental transitions, a lower applied stress is needed to deform the SMP resulting from a large number of soft components. As is well known, an external stress is needed to achieve the elemental transition resulting from the change in entropy of the macromolecule chains according to the thermodynamics of polymers [39]
decreases with the increase in the elemental transitions. With more elemental transitions, a lower applied stress is needed to deform the SMP resulting from a large number of soft components. As is well known, an external stress is needed to achieve the elemental transition resulting from the change in entropy of the macromolecule chains according to the thermodynamics of polymers [39]
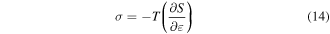
where  is the stretching stress,
is the stretching stress, 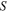 is the change in entropy of the polymer chains and
is the change in entropy of the polymer chains and 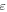 is the strain. Equation (14) reveals that a higher stretching stress is required for more elemental transitions in the polymer. That is to say, the internal stress is gradually increased due to the increased stretching stress that is used for an increase in the
is the strain. Equation (14) reveals that a higher stretching stress is required for more elemental transitions in the polymer. That is to say, the internal stress is gradually increased due to the increased stretching stress that is used for an increase in the 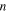 elemental transitions.
elemental transitions.
Figure 4. Applied stress against internal stress curves of the polymer with  elementary transitions: (a) at a given strain rate ratio, where
elementary transitions: (a) at a given strain rate ratio, where  = 2, 4, 5, 8 and 10, and (b) at a given number of elementary transitions, where
= 2, 4, 5, 8 and 10, and (b) at a given number of elementary transitions, where 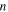 = 2, 4, 5, 8 and 10.
= 2, 4, 5, 8 and 10.
Download figure:
Standard image High-resolution imageThe shape recovery behaviour of SMPs results from the structural relaxation and viscoelastic transition of polymer macromolecules. The viscoelastic properties of an SMP are generally characterized by dynamic mechanical analysis (DMA). The storage modulus is temperature dependent based on the viscoelastic theory and DMA measurement. According to Gilbert et al [41], the drop in the storage modulus  caused by thermal expansion can be written as
caused by thermal expansion can be written as
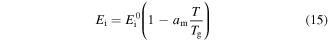
where 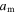 is a dimensionless thermal expansion coefficient and
is a dimensionless thermal expansion coefficient and  is the storage modulus at 0 K.
is the storage modulus at 0 K. 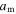 is related to the potential barriers and the dimensions of the polymeric macromolecules. Equation (15) could be used for both the dynamic modulus and the static modulus. The internal stress is related to the storage modulus and strain by [42]
is related to the potential barriers and the dimensions of the polymeric macromolecules. Equation (15) could be used for both the dynamic modulus and the static modulus. The internal stress is related to the storage modulus and strain by [42]
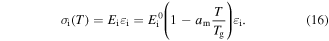
In a previous work on the TME in SMPs [40], the experimental results were employed to verify the theoretical investigation. Table 1 presents the storage modulus of the polymer deformed at 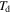 = 70 °C, 90 °C, 120 °C, 150 °C and 180 °C. It was claimed that the deformation temperature was the
= 70 °C, 90 °C, 120 °C, 150 °C and 180 °C. It was claimed that the deformation temperature was the  in the shape recovery of the polymer, where
in the shape recovery of the polymer, where  =
=  Based on the experimental results of the storage modulus, the dimensionless thermal expansion coefficient
Based on the experimental results of the storage modulus, the dimensionless thermal expansion coefficient  could be obtained according to equation (15), where
could be obtained according to equation (15), where 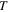 (
(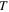 = 323 K, 348 K, 373 K, 398 K, 423 K, 448 K or 473 K) and
= 323 K, 348 K, 373 K, 398 K, 423 K, 448 K or 473 K) and 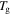 (
(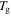 =
= 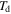 = 343 K, 363 K, 393 K, 423 K or 453 K) are as shown in table 2. The experimental data for the SMP at two deformation temperatures of 343 K and 363 K are used in this study, and
= 343 K, 363 K, 393 K, 423 K or 453 K) are as shown in table 2. The experimental data for the SMP at two deformation temperatures of 343 K and 363 K are used in this study, and  (where
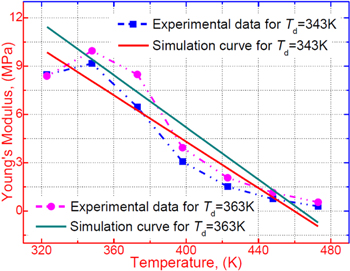
(where  ) is calculated as 2.175 × 10–3 K−1 and 2.154 × 10-3 K−1, respectively. The theoretical results for the storage modulus are plotted in figure 5, according to equation (15). Experimental data are also plotted for comparison. It was found that the theoretical simulation results were in good agreement with the experimental results for the SMP deformed at 343 K and 363 K. A linear relationship between the storage modulus and the temperature was confirmed.
) is calculated as 2.175 × 10–3 K−1 and 2.154 × 10-3 K−1, respectively. The theoretical results for the storage modulus are plotted in figure 5, according to equation (15). Experimental data are also plotted for comparison. It was found that the theoretical simulation results were in good agreement with the experimental results for the SMP deformed at 343 K and 363 K. A linear relationship between the storage modulus and the temperature was confirmed.
Table 1.
Storage modulus 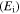 data from the experimental curves for the SMP with different deformation temperatures.
data from the experimental curves for the SMP with different deformation temperatures.
| T (K) | Ei (Td = 343 K) | Ei (Td = 363 K) | Ei (Td = 393 K) | Ei (Td = 423 K) | Ei (Td = 453 K) |
|---|---|---|---|---|---|
| 323 | 8.47 MPa | 8.38 MPa | 2.87 MPa | 2.12 MPa | 1.29 MPa |
| 348 | 9.16 MPa | 9.94 MPa | 5.79 MPa | 5.14 MPa | 2.33 MPa |
| 373 | 6.46 MPa | 8.48 MPa | 6.09 MPa | 6.21 MPa | 3.27 MPa |
| 398 | 3.06 MPa | 3.93 MPa | 4.84 MPa | 5.45 MPa | 3.36 MPa |
| 423 | 1.51 MPa | 2.06 MPa | 2.82 MPa | 4.46 MPa | 3.51 MPa |
| 448 | 0.743 MPa | 1.14 MPa | 1.89 MPa | 2.21 MPa | 2.66 MPa |
| 473 | 0.293 MPa | 0.544 MPa | 1.14 MPa | 0.787 MPa | 1.43 MPa |
Table 2.
Dimensionless thermal expansion coefficient  data for the SMP with different deformation temperatures.
data for the SMP with different deformation temperatures.
| T (K) | am/Tg (Td = 343 K) | am/Tg (Td = 363 K) | am/Tg (Td = 393 K) | am/Tg (Td = 423 K) | am/Tg (Td = 453 K) |
|---|---|---|---|---|---|
| 323 | 0.062 05 | 0.005 299 | 0.003 351 | 0.003 274 | 0.003 425 |
| 348 | 0.002 452 | 0.002 028 | −0.006 27 | 0.004 928 | 0.003 831 |
| 373 | 0.002 699 | 0.002 706 | 0.002 248 | 0.001 897 | −0.001 71 |
| 398 | 0.002 686 | 0.002 663 | 0.002 612 | 0.002 171 | −0.004 22 |
| 423 | 0.002 687 | 0.002 639 | 0.002 507 | 0.002 684 | 0.002 346 |
| 448 | 0.002 745 | 0.002 697 | 0.002 591 | 0.002 764 | 0.002 652 |
| 473 | 0.002 874 | 0.002 874 | 0.002 874 | 0.002 874 | 0.002 874 |
Figure 5. Storage modulus as a function of temperature for the SMP with a deformation transition temperature of 343 K and 363 K. A comparison is shown between the previous experimental data obtained from reference [40] and the fitting plots of equation (15).
Download figure:
Standard image High-resolution imageIt has been identified that the stored mechanical energy 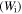 plays an essential role in determining the temperature memory behaviour [43, 44]. The stored mechanical energy is given by
plays an essential role in determining the temperature memory behaviour [43, 44]. The stored mechanical energy is given by
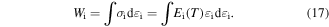
Combining equations (15) and (17), the stored mechanical energy can be described by
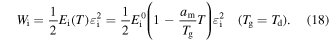
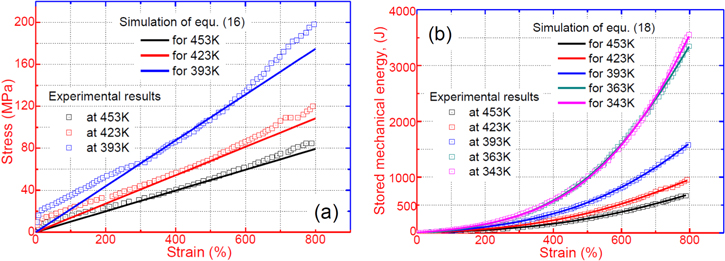
Figure 6 plots the numerical results for the effect of strain on the stress and stored mechanical energy of an SMP with different strain and temperature parameters, respectively. Experimental data are also plotted for comparison. It was found that the theoretical simulation results were in good agreement with the experimental results. In figure 6(a), the simulation results reveal that the stress is gradually increased with the increase in strain. With the deformation temperature increased from 393 K, 423 K to 453 K, a lower stress is needed to stretch the tested sample to the same stretching ratio (as for a given strain). Therefore, a lower stored mechanical energy is then stored in the tested sample, resulting from a higher deformation temperature and lower stress according to equations (16) and (18), as shown in figure 6(b). These simulation results confirm that the stored mechanical energy 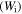 is strongly determined by the strain and temperature. For a given SMP, a higher stored mechanical energy is required for greater deformation (e.g., to a larger stretching ratio). However, the stored mechanical energy is depressed by the temperature increase due to the stored mechanical energy being released and used to drive the shape recovery of the SMP. For a given stretching ratio (or deformation), the mechanical energy is stored in the SMP, as the deformation is retained during cooling to room temperature. A higher mechanical energy is stored resulting from a higher deformation temperature according to equation (18). The stored mechanical energy is then used to drive the shape recovery of the SMP by means of structural relaxation of macromolecules when it is again heated above
is strongly determined by the strain and temperature. For a given SMP, a higher stored mechanical energy is required for greater deformation (e.g., to a larger stretching ratio). However, the stored mechanical energy is depressed by the temperature increase due to the stored mechanical energy being released and used to drive the shape recovery of the SMP. For a given stretching ratio (or deformation), the mechanical energy is stored in the SMP, as the deformation is retained during cooling to room temperature. A higher mechanical energy is stored resulting from a higher deformation temperature according to equation (18). The stored mechanical energy is then used to drive the shape recovery of the SMP by means of structural relaxation of macromolecules when it is again heated above 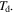 In the free shape recovery process, a higher stored mechanical energy must result in a higher transition temperature on the origin of the Arrhenius rule, which implies that the relaxation time is only determined by the internal energy and temperature parameters. The TME results from the stored mechanical energy, and the effect on the relaxation behaviour or shape recovery behaviour of an SMP is achieved by means of internal (recovery) stress. This is the mechanism for the TME in SMPs.
In the free shape recovery process, a higher stored mechanical energy must result in a higher transition temperature on the origin of the Arrhenius rule, which implies that the relaxation time is only determined by the internal energy and temperature parameters. The TME results from the stored mechanical energy, and the effect on the relaxation behaviour or shape recovery behaviour of an SMP is achieved by means of internal (recovery) stress. This is the mechanism for the TME in SMPs.
Figure 6. (a) Stress as a function of strain for an SMP with deformation transition temperatures of 393 K, 423 K and 453 K. A comparison is shown between the previous experimental data obtained from [40] and the fitting plots of equation (16). (b) Stored mechanical energy as a function of strain for an SMP with deformation transition temperatures of 343 K, 363 K, 393 K, 423 K and 453 K. A comparison is shown between the previous experimental data obtained from [40] and the fitting plots of equation (18).
Download figure:
Standard image High-resolution image4. Cooperative model for the chemo-responsive SME
Essentially, the working mechanism for the chemo-responsive SME in SMPs is the same as that for thermo-responsive SMPs by means of the plasticizing effect or swelling effect, instead of being activated by heating to above the transition temperature [45–48]. Studies on the theoretical framework for the chemo-responsive SME have also been conducted [49–54]. The chemical plasticizing effect of water or solvent has been identified as one of the driving forces for softening SMPs [49–51]. However, almost all previous works were carried out according to the plasticizing effect on the relaxation behaviour of the whole polymer macromolecules, where the difference in the components is not considered. According to equation (6), the Arrhenius law and the WLF equation were employed to characterize the effect of strain rate on the relaxation behaviour of a polymer below and above  respectively. Here,
respectively. Here, 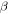 and
and  relaxations have been named as the viscoelastic behaviour below and above
relaxations have been named as the viscoelastic behaviour below and above 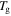 of the polymer, respectively. The characteristic strain rate above
of the polymer, respectively. The characteristic strain rate above 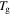 is expressed as [29]
is expressed as [29]
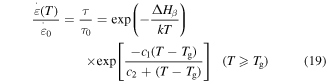
where  is the relaxation time and
is the relaxation time and  is a given constant. All parameters in the above equation have been defined previously. It has been identified that the influence of the plasticizers is to lower the temperature at which
is a given constant. All parameters in the above equation have been defined previously. It has been identified that the influence of the plasticizers is to lower the temperature at which 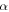 relaxation occurs while
relaxation occurs while  relaxation is largely unaffected. Thus in the cooperative Eyring model for relaxation, the free energy of the polymer is lowered owing to its depression effect on the
relaxation is largely unaffected. Thus in the cooperative Eyring model for relaxation, the free energy of the polymer is lowered owing to its depression effect on the  transition [55]. That is to say, the plasticizing effect of water or solvent on the relaxation behaviour of the SMP is due to the depression in
transition [55]. That is to say, the plasticizing effect of water or solvent on the relaxation behaviour of the SMP is due to the depression in 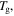 but not for
but not for 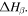
In this manner, the curves for relaxation time against temperature above  (assuming
(assuming  = 373 K in this theoretical calculation) are plotted in figure 7. The plasticizing effect of water or solvent on the polymer is achieved by means of depressing
= 373 K in this theoretical calculation) are plotted in figure 7. The plasticizing effect of water or solvent on the polymer is achieved by means of depressing 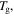 as shown in figures 7(a) and (b). These results reveal that the relaxation time is significantly decreased, resulting in a wet SMP with a short recovery time in comparison with that of a dry one, although the
as shown in figures 7(a) and (b). These results reveal that the relaxation time is significantly decreased, resulting in a wet SMP with a short recovery time in comparison with that of a dry one, although the 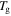 is depressed slightly.
is depressed slightly.
Figure 7. Numerical results of the normalized relaxation time 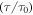 against temperature of the polymer. (a)
against temperature of the polymer. (a) 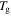 is inductively depressed from
is inductively depressed from 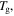 0.095
0.095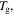 0.990
0.990 0.985
0.985 to 0.980
to 0.980 by the plasticizers. (b)
by the plasticizers. (b) 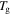 is inductively depressed from
is inductively depressed from 
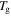 -1 K,
-1 K,  -2 K,
-2 K, 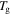 -3 K to
-3 K to  -4 K by the plasticizers.
-4 K by the plasticizers.
Download figure:
Standard image High-resolution imageAdditionally, the chemo-responsive SME in SMPs can also be achieved by terms of the swelling effect of the solvent. Here the swelling effect on the relaxation behaviour of an SMP is essential to quantitatively separate the influential factors and identify their working mechanism. For the activation enthalpy, for temperatures below and above  and using the cooperative Eyring model [56], we have
and using the cooperative Eyring model [56], we have
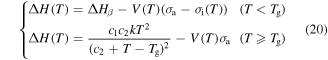
As for the Eyring model, it was found that the activation enthalpy given by equation (20) was composed of two separate entities. The first represents the activation energy in the absence of all stresses and the second contributes to the presence of applied stress and internal stress. As discussed above, the solvent plasticizers have strong influence on the  relaxation of the polymer. In the case of free shape recovery, no externally applied stress is applied to the SMP, assuming
relaxation of the polymer. In the case of free shape recovery, no externally applied stress is applied to the SMP, assuming  = 0,
= 0,
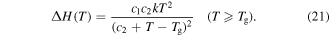
On the other hand, a synergistic effect of the plasticizing effect and swelling effect is not considered, that is to say, only the swelling effect of the plasticizers was involved in achieving the chemo-responsive SME in SMPs. Therefore, the 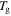 of the SMP is not depressed by the swelling effect, resulting in the activation enthalpy being depressed,
of the SMP is not depressed by the swelling effect, resulting in the activation enthalpy being depressed,
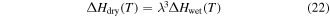
where  is the activation enthalpy of the dry SMP,
is the activation enthalpy of the dry SMP,  is the activation enthalpy of the swollen SMP resulting from the swelling effect of the plasticizers,
is the activation enthalpy of the swollen SMP resulting from the swelling effect of the plasticizers, 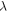
 is the stretching ratio and
is the stretching ratio and 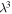 is the swollen volume in comparison with the dry volume. It was revealed that the increase in stretching ratio is analogous to the decrease in
is the swollen volume in comparison with the dry volume. It was revealed that the increase in stretching ratio is analogous to the decrease in 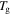 for a given relaxation time according to the Eyring equation,
for a given relaxation time according to the Eyring equation,

where 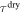 and
and 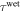 are the relaxation times of the SMP for its unswollen and swollen state, respectively.
are the relaxation times of the SMP for its unswollen and swollen state, respectively. 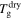 and
and 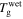 are the glass transition temperatures of the SMP for its unswollen and swollen state, respectively. After combination of equations (22) and (23),
are the glass transition temperatures of the SMP for its unswollen and swollen state, respectively. After combination of equations (22) and (23),
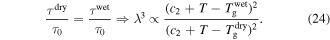
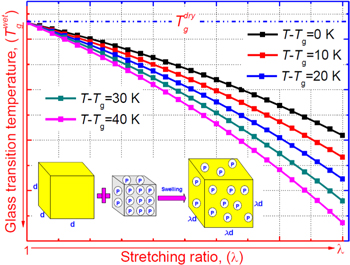
Figure 8 plots numerical results for  of the swollen SMP at a given temperature above
of the swollen SMP at a given temperature above  With an increase in the stretching ratio,
With an increase in the stretching ratio, 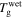 of the SMP gradually decreases, which is attributable to the decrease in activation enthalpy according to equation (22). When a polymer is swollen by a solvent, the activation enthalpy (or energy) per volume then decreases according to the Flory–Huggins solution theory. On the other hand, the storage modulus, which is a reflection of the internal energy in a polymer, also gradually decreases with the volume increase based on the rubber elastic theory [51]. In this manner,
of the SMP gradually decreases, which is attributable to the decrease in activation enthalpy according to equation (22). When a polymer is swollen by a solvent, the activation enthalpy (or energy) per volume then decreases according to the Flory–Huggins solution theory. On the other hand, the storage modulus, which is a reflection of the internal energy in a polymer, also gradually decreases with the volume increase based on the rubber elastic theory [51]. In this manner, 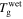 in the SMP is inductively depressed, resulting in the shape recovery achieved by the swelling effect, instead of direct heating. Therefore, the decrease in activation enthalpy (or energy) is the working mechanism for the chemo-responsive SME in SMPs. It should be noted that the decrease in the activation enthalpy (or energy) resulting from the
in the SMP is inductively depressed, resulting in the shape recovery achieved by the swelling effect, instead of direct heating. Therefore, the decrease in activation enthalpy (or energy) is the working mechanism for the chemo-responsive SME in SMPs. It should be noted that the decrease in the activation enthalpy (or energy) resulting from the 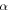 relaxation of polymer macromolecules plays an essential role in determining the chemo-responsive shape recovery behaviour of SMPs.
relaxation of polymer macromolecules plays an essential role in determining the chemo-responsive shape recovery behaviour of SMPs.
Figure 8. Numerical results of 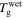 of the swollen SMP against stretching ratio at given temperatures
of the swollen SMP against stretching ratio at given temperatures 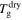 + 0 K,
+ 0 K,  + 10 K,
+ 10 K,  + 20 K,
+ 20 K, 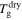 + 30 K or
+ 30 K or 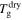 + 40 K.
+ 40 K.
Download figure:
Standard image High-resolution image5. Conclusion
In this study, we proposed a theoretical framework for studying the multi-shape/temperature memory effect in an amorphous SMP with multi-stress components based on the Eyring cooperative model. It was demonstrated that the proposed constitutive framework is able to describe well the multi-SME, TME and chemo-responsive SME and predict their shape memory behaviour in SMPs. This provides an effective way of estimating and quantitatively separating the dependence of the SME and TME on the internal (recovery) stress, stored mechanical energy, and activation enthalpy (energy) functions. The working mechanism in the thermo-responsive SME and TME in SMPs was identified, and found to be ruled by both the internal (recovery) stress and stored mechanical energy. The chemo-responsive SME results from the inductive depression in activation enthalpy (energy) and transition temperature, while the working mechanism is the same as that of the thermo-responsive SME. The accuracy of the analytical results was then examined based on the experimental results. This study is expected to provide a powerful tool for exploring the working mechanisms in shape/temperature memory behaviour in amorphous SMPs.
Acknowledgments
This work was financially supported by the National Natural Science Foundation of China (NSFC) under Grant No. 11422217 and 11672342, Program for New Century Excellent Talents in University under Grant No. NCET-13-0172, Foundation for the Author of National Excellent Doctoral Dissertation of the People's Republic of China (Grant No. 201328) and National Youth Top-notch Talent Support Program.