Abstract
In this paper, we study the p-Laplacian equation with a Lp-norm constraint: 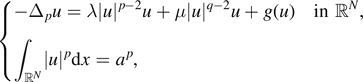 where N ⩾ 2, a > 0,
where N ⩾ 2, a > 0,  ,
, 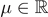 ,
, 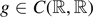 and
and 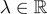 is a Lagrange multiplier, which appears due to the mass constraint ||u||p = a. We assume that g is odd and Lp-supercritical. When
is a Lagrange multiplier, which appears due to the mass constraint ||u||p = a. We assume that g is odd and Lp-supercritical. When  and μ > 0, we use Schwarz rearrangement and Ekeland variational principle to prove the existence of positive radial ground states for suitable μ. When
and μ > 0, we use Schwarz rearrangement and Ekeland variational principle to prove the existence of positive radial ground states for suitable μ. When 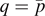 and μ > 0 or
and μ > 0 or 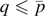 and μ ⩽ 0, with an additional condition of g, we obtain a positive radial ground state if μ lies in a suitable range, by the Schwarz rearrangement and minimax theorems. Via a fountain theorem type argument, with suitable
and μ ⩽ 0, with an additional condition of g, we obtain a positive radial ground state if μ lies in a suitable range, by the Schwarz rearrangement and minimax theorems. Via a fountain theorem type argument, with suitable  , we obtain infinitely many radial solutions for any N ⩾ 2 and establish the existence of infinitely many nonradial sign-changing solutions for N = 4 or N ⩾ 6. In any case mentioned above, the range of μ depends on the value of a: |μ| can be large if a > 0 is small.
, we obtain infinitely many radial solutions for any N ⩾ 2 and establish the existence of infinitely many nonradial sign-changing solutions for N = 4 or N ⩾ 6. In any case mentioned above, the range of μ depends on the value of a: |μ| can be large if a > 0 is small.
Export citation and abstract BibTeX RIS
Recommended by Dr Susanna Terracini
Footnotes
- *


