Ground state solutions for critical Schrödinger equations with Hardy potential

In this paper, we investigate the following Schrödinger equation

$$\begin{equation}-{\Delta}u-\frac{\mu }{\vert x{\vert }^{2}}u=g(u)+\vert u{\vert }^{{2}^{\ast }-2}u\ \ \ \ \mathrm{i}\mathrm{n}\ {\mathbb{R}}^{N}{\backslash}\left\{0\right\},\end{equation} \tag{ 0.1 }$$

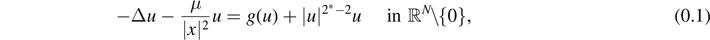
where N ⩾ 3, 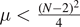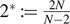$\mu < \frac{{(N-2)}^{2}}{4}$, ${2}^{\ast }{:=}\frac{2N}{N-2}$ is called the critical Sobolev exponent and g satisfies some appropriate subcritical conditions. For any 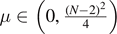$\mu \in \left(0,\frac{{(N-2)}^{2}}{4}\right)$, we prove that problem (0.1) has a positive radial ground state solution, which possesses exponential decaying property at infinity and blow-up property at origin. Moreover, for any sequence {μ_n} ⊂ (0, +∞) satisfying μ_n → 0⁺, the sequence of ground state solutions to problem (0.1) converges to a ground state solution of

$$\begin{equation}-{\Delta}u=g(u)+\vert u{\vert }^{{2}^{\ast }-2}u\ \ \ \ \mathrm{i}\mathrm{n}\ {\mathbb{R}}^{N}.\end{equation} \tag{ 0.2 }$$

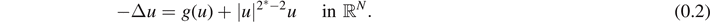
when μ < 0, we prove that the mountain pass level of problem (0.1) in 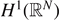${H}^{1}({\mathbb{R}}^{N})$ cannot be achieved. Further, we obtain a ground state radial solution of problem (0.1) whose energy is strictly greater than the mountain pass level in ${H}^{1}({\mathbb{R}}^{N})$. Also, for any sequence {μ_n} ⊂ (0, +∞) satisfying μ_n → 0⁺, the sequence of ground state radial solutions to problem (0.1) converges to a ground state radial solution of the limiting problem as n → ∞.