Abstract
We present a theory of the Seebeck effect in nanomagnets with dimensions smaller than the spin diffusion length, showing that the spin accumulation generated by a temperature gradient strongly affects the thermopower. We also identify a correction arising from the transverse temperature gradient induced by the anomalous Ettingshausen effect and an induced spin-heat accumulation gradient. The relevance of these effects for nanoscale magnets is illustrated by ab initio calculations on dilute magnetic alloys.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Spin caloritronics [1–3] addresses the coupling between the spin and heat transport in small structures and devices. The effects addressed so far can be categorized into several groups [2]. The first group covers phenomena whose origin is not connected to spin–orbit coupling (SOC). Nonrelativistic spin caloritronics in magnetic conductors addresses thermoelectric effects in which motion of electrons in a thermal gradient drives spin transport, such as the spin-dependent Seebeck [4] and the reciprocal Peltier [5, 6] effect. Another group of phenomena is caused by SOC and belongs to relativistic spin caloritronics [2] including the anomalous [7] and spin [8–12] Nernst effects.
The Seebeck effect [13] or thermopower stands for the generation of an electromotive force or gradient of the electrochemical potential μ by temperature gradients ∇T. The Seebeck coefficient S parameterizes the proportionality when the charge current j vanishes:
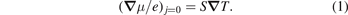
In the two-current model for spin-polarized systems, the thermopower of a magnetic metal reads
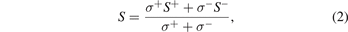
where σ± and S± are the spin-resolved longitudinal conductivities and Seebeck coefficients, respectively.
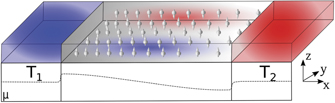
Here, we study the Seebeck effect in nanoscale magnets on scales equal or less than their spin diffusion length [14] as in figure 1. Thermal baths on both sides of the sample drive a heat current in the x direction. Since no charge current flows, a thermovoltage builds up at the sample edges that can be observed non-invasively by tunnel junctions or scanning probes. Note that metallic contacts can detect the thermovoltage at zero-current bias conditions, but this requires additional modelling of the interfaces. We show in the following that in the presence of a thermally generated spin accumulation the thermopower differs from equation (2). We then focus on dilute ternary alloys of a Cu host with magnetic Mn and nonmagnetic Ir impurities. By varying the alloy concentrations we may tune to the unpolarized case S+ = S−, as well as to spin-dependent S+ and S− parameters with equal or opposite signs. The single-electron thermoelectric effects considered here can be distinguished from collective magnon drag effects [15] by their temperature dependence.
Figure 1. We consider a ferromagnetic metal slab smaller than the spin diffusion length in contact with two thermal baths hot (red) and cold (blue) that generate a temperature gradient in the x direction. The spheres with arrows represent the excited electrons with spin up and down parallel to the magnetization. The thermally induced electrons are represented by their density as well as a gradient in the grey scale of the background. The red and blue clouds indicate transverse heat accumulation (in the y direction). The dash-dotted line is the chemical potential μ for a high interface resistance to the contacts.
Download figure:
Standard image High-resolution image2. Theory
In the two-current model of spin transport in a single-domain magnet [16–18], extended to include heat transport, the charge ( j ) and heat ( q ) current densities read
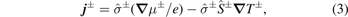
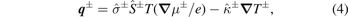
where 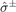 ,
, 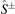 , and
, and 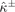 are the spin-resolved electric conductivity, Seebeck coefficient, and heat conductivity, respectively. All transport coefficients are tensors that reflect crystalline symmetry and SOC. The 'four-current model' equations (3) and (4) can be rewritten as
are the spin-resolved electric conductivity, Seebeck coefficient, and heat conductivity, respectively. All transport coefficients are tensors that reflect crystalline symmetry and SOC. The 'four-current model' equations (3) and (4) can be rewritten as
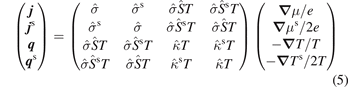
in terms of the charge
j
=
j
+ +
j
−, spin
j
s =
j
+ −
j
−, heat
q
=
q
+ +
q
−, and spin-heat
q
s =
q
+ −
q
− current densities. Here, we introduced the conductivity tensors for charge 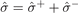 , spin
, spin 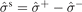 , heat
, heat 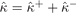 , and spin heat
, and spin heat  . The driving forces are
. The driving forces are

and the gradients of the spin μs = μ+ − μ− [18–21] and spin-heat Ts = T+ − T− accumulations [2, 22–27]
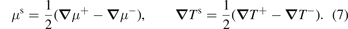
Finally, the tensors
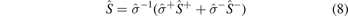
and

in equation (5) describe the charge and spin-dependent Seebeck coefficients, respectively. In cubic systems the diagonal component Sii , where i is the Cartesian component of the applied temperature gradient, reduces to the scalar thermopower equation (2).
3. Results
In the following we apply equation (5) to the Seebeck effect in nanoscale magnets assuming their size to be smaller than the spin diffusion length. In this case the spin-flip scattering may be disregarded [28]. We focus first on longitudinal transport and disregard ∇ Ts. However, we also discuss transverse (Hall) effects as well as the spin temperature gradient below. We adopt open-circuit conditions for charge and spin transport under a temperature gradient. Charge currents and, since we disregard spin-relaxation, spin currents vanish everywhere in the sample:
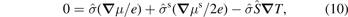
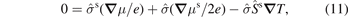
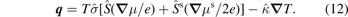
The thermopower now differs from the conventional expression given by equation (2). Let us introduce the tensor  as
as
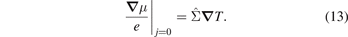
From equations (10) and (11), we find

When the spin accumulation in equation (10) vanishes we recover 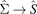 . Equation (14) involves only directly measurable material parameters [29], but the physics is clearer in the compact expression
. Equation (14) involves only directly measurable material parameters [29], but the physics is clearer in the compact expression
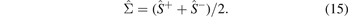
The spin polarization of the Seebeck coefficient

reads

or
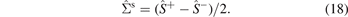
The diagonal elements of 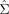 govern the thermovoltage in the direction of the temperature gradient. The off-diagonal elements of
govern the thermovoltage in the direction of the temperature gradient. The off-diagonal elements of 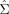 represent transverse thermoelectric phenomena such as the anomalous [7] and planar [30] Nernst effects. The diagonal and off-diagonal elements of
represent transverse thermoelectric phenomena such as the anomalous [7] and planar [30] Nernst effects. The diagonal and off-diagonal elements of 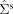 describe the spin-dependent Seebeck effect [2, 4], as well as (also in non-magnetic systems) the spin and planar-spin Nernst effects [8–12], respectively. We do not address here anomalous and Hall transport in the purely charge and heat sectors of equation (5).
describe the spin-dependent Seebeck effect [2, 4], as well as (also in non-magnetic systems) the spin and planar-spin Nernst effects [8–12], respectively. We do not address here anomalous and Hall transport in the purely charge and heat sectors of equation (5).
3.1. Longitudinal spin accumulation
A temperature gradient in x direction ∇ T ∥ e x induces the voltage in the same direction:
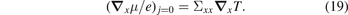
In order to assess the importance of the difference between equations (14) and (15) and the conventional thermopower equation (2) we carried out first-principles transport calculations for the ternary alloys Cu1−v (Mn1−w Irw ) v , where w ∈ [0, 1] and the total impurity concentration is fixed to v = 1 at.% [31]. We have chosen this system as a generic example where the Cu host ensures a reasonably large spin diffusion length and the two impurities allow us to scale easily between the different limits of strong spin-dependent scattering induced by magnetism for Cu(Mn) and SOC for Cu(Ir). The derived expressions equally apply to more conventional ferromagnets as long the dimensions of the sample is comparable or smaller than the spin diffusion length. We calculate the transport properties from the solutions of the linearized Boltzmann equation with collision terms calculated for isolated impurities [32, 33]. We disregard spin-flip scattering [33], which limits the size of the systems for which our results hold (see below). We calculate the electronic structure of the Cu host by the relativistic Korringa–Kohn–Rostoker method [34]. Figure 2 summarizes the calculated room-temperature (charge) thermopower equation (8) or (14) and (15) and their spin-resolved counterparts, equations (17) and (18). Table 1 contains additional information for the binary alloys Cu(Mn) and Cu(Ir) with w = 0 or w = 1 in figure 2, respectively. Here we implicitly assume an applied magnetic field that orders all localized moments.
Figure 2. The diagonal thermopowers S and Σ, equations (8) and (14), respectively, as well as the spin-resolved thermopowers S± as calculated for dilute Cu(Mn1−w Irw ) alloys at 300 K with the total impurity concentration 1 at.%.
Download figure:
Standard image High-resolution imageTable 1. Computed spin-resolved and charge thermopowers as defined in the text for magnetic Cu0.99Mn0.01 and Cu0.99(Mn0.5Ir0.5)0.01 as well as non-magnetic Cu0.99Ir0.01 dilute alloys. The conventional spin Seebeck coefficient is shown for comparison. All quantities are calculated at 300 K in units of μV K−1.
| System | Cu0.99Mn0.01 | Cu0.99(Mn0.5Ir0.5)0.01 | Cu0.99Ir0.01 |
|---|---|---|---|

| −6.87 | −7.01 | −7.09 |
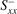
| 8.57 | 1.64 | −7.09 |
| Sxx | −6.14 | −4.26 | −7.09 |
| Σxx | 0.85 | −2.69 | −7.09 |
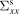
| −7.72 | −4.33 | 0.00 |
We observe large differences (even sign changes) between 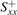 and
and  that causes significant differences between
that causes significant differences between 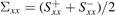 and the macroscopic Sxx
. The complicated behavior of the latter is caused by the weighting of S+ and S− by the corresponding conductivities, see equation (8). Even though a spin-accumulation gradient suppresses the Seebeck effect, an opposite sign of
and the macroscopic Sxx
. The complicated behavior of the latter is caused by the weighting of S+ and S− by the corresponding conductivities, see equation (8). Even though a spin-accumulation gradient suppresses the Seebeck effect, an opposite sign of 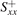 and
and 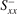 can enhance
can enhance  beyond the microscopic as well as macroscopic thermopower. Indeed, Hu et al [35] observed a spin-dependent Seebeck effect that is larger than the charge Seebeck effect in CoFeAl. Our calculations illustrate that the spin-dependent Seebeck effect can be engineered and maximized by doping a host material with impurities.
beyond the microscopic as well as macroscopic thermopower. Indeed, Hu et al [35] observed a spin-dependent Seebeck effect that is larger than the charge Seebeck effect in CoFeAl. Our calculations illustrate that the spin-dependent Seebeck effect can be engineered and maximized by doping a host material with impurities.
3.2. Hall transport
In the presence of spin–orbit interactions the applied temperature gradient ∇ Text induces anomalous Hall currents. When the electron–phonon coupling is weak, the spin–orbit interaction can, for example, induce transverse temperature gradients. In a cubic magnet the charge and spin conductivity tensors are antisymmetric. With magnetization and spin quantization axis along z:
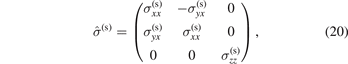
and analogous expressions hold for 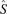 and
and  . A charge current in the x direction generates a transverse heat current that heats and cools opposite edges, respectively. A transverse temperature gradient
∇
Tind ∥
e
y
is signature of this anomalous Ettingshausen effect [36] gradient. From equations (12), (13), and (16)
. A charge current in the x direction generates a transverse heat current that heats and cools opposite edges, respectively. A transverse temperature gradient
∇
Tind ∥
e
y
is signature of this anomalous Ettingshausen effect [36] gradient. From equations (12), (13), and (16)
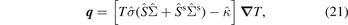
where ∇ T = e x ∇x Text + e y ∇y Tind. Assuming weak electron-phonon scattering, the heat cannot escape the electron systems and qy = 0. equation (21) then leads to
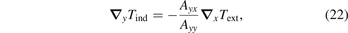
where Ayx and Ayy are components of the tensor
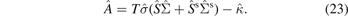
Consequently, equation (13) leads to a correction to the thermopower
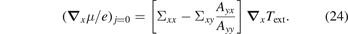
However, this effect should be small [37–40] for all but the heaviest elements but may become observable when Σxx vanishes, which according to figure 2 should occur at around w = 0.125.
3.3. Spin temperature gradient
At low temperatures, the spin temperature gradient ∇ Ts may persist over length scales smaller but of the same order as the spin accumulation [25]. From equations (3), (15), and (18) it follows


Starting with equation (5) and employing equations (25) and (26) for the heat and spin-heat current densities we obtain
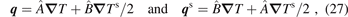
where
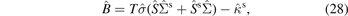
and  is defined by equation (23). With
is defined by equation (23). With  and
∇
T =
e
x
∇x
Tex +
e
y
∇y
Tin we find
and
∇
T =
e
x
∇x
Tex +
e
y
∇y
Tin we find
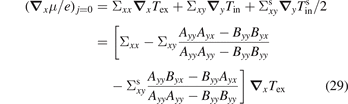
assuming again qy
= 0 and 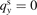 . Similar to equation (24), the Hall corrections in equation (29) should be significant only when Σxx
vanishes for w = 0.125. However, experimentally it might be difficult to separate the thermopowers equations (29) and (24).
. Similar to equation (24), the Hall corrections in equation (29) should be significant only when Σxx
vanishes for w = 0.125. However, experimentally it might be difficult to separate the thermopowers equations (29) and (24).
3.4. Spin diffusion length and mean free path
Our first-principles calculation are carried out for bulk dilute alloys based on Cu and in the single site approximation of spin-conserving impurity scattering. The Hall effects are therefore purely extrinsic. This is an approximation that holds on length scales smaller than various spin diffusion lengths lsf. On the other hand, the Boltzmann equation approach is valid when the sample is larger than the elastic scattering mean free path l, so our results should be directly applicable for sample lengths L that fulfill l < L ⩽ lsf. According to references [37, 40], for the ternary alloy Cu(Mn0.5Ir0.5) with impurity concentration of 1 at.% the present results hold on length scales 26 nm 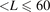 nm and 100 nm
nm and 100 nm 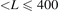 nm for Cu(Mn). On the other hand, for nonmagnetic Cu(Ir) the applicability is limited to a smaller interval 10 nm
nm for Cu(Mn). On the other hand, for nonmagnetic Cu(Ir) the applicability is limited to a smaller interval 10 nm 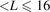 nm. We believe that while the results outside these strict limits may not be quantitatively reliable, they still give useful insights into trends.
nm. We believe that while the results outside these strict limits may not be quantitatively reliable, they still give useful insights into trends.
4. Summary and outlook
In summary, we derived expressions for the thermopower valid for ordered magnetic alloys for sample sizes that do not exceed the spin diffusion lengths (that have to be calculated separately). We focus on dilute alloys of Cu with Mn and Ir impurities. For 1% ternary alloys Cu(Mn1−w Irw ) with w < 0.5 the spin diffusion length is lsf > 60 nm. In this regime the spin and charge accumulations induced by an applied temperature gradient strongly affect each other. By ab initio calculations of the transport properties of Cu(Mn1−w Irw ) alloys, we predict thermopowers that drastically differ from the bulk value even changing sign. Relativistic Hall effects generate spin accumulations normal to the applied temperature gradient that become significant when the longitudinal thermopower Σxx vanishes, for example for Cu(Mn1−w Irw ) alloys at w ≈ 0.125.
After having established the principle existence of the various corrections to the conventional transport description it would be natural to move forward to describe extended thin films. A first-principles version of the Boltzmann equation including all electronic spin non-conserving scatterings in extended films is possible, but very expensive for large lsf. It would still be incomplete, since the relaxation of heat to the lattice by electron-phonon interactions and spin-heat by electron–electron scattering [23, 24] are not included. We therefore propose to proceed pragmatically: The regime l < lsf < L is accessible to spin-heat diffusion equations that can be parameterized by first-principles material-dependent parameters as presented here and relaxation lengths that may be determined otherwise, such as by fitting to experimental results.
Acknowledgments
This work was partially supported by the Deutsche Forschungsgemeinschaft via SFB 762 and the priority program SPP 1538 as well as JSPS Grants-in-Aid for Scientific Research (KAKENHI Grant No. 19H00645). MG acknowledges financial support from the Leverhulme Trust via an Early Career Research Fellowship (ECF-2013-538) and a visiting professorship at the Centre for Dynamics and Topology of the Johannes-Gutenberg-University Mainz.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.