Recent advances in topological elastic metamaterials

Metamaterials, mainly referring to artificial composite materials or structures with unconventional properties [1–3], have become a research hotspot over the past decade. Their extraordinary wave manipulation capabilities, originated from component structures or unit cells with an ingenious configuration design [4], lead to many intriguing physical effects and promising applications, including wave transformation [5], super-resolution imaging [6], and cloaking [7]. Early efforts on metamaterials focused on controlling electromagnetic waves with desirable optical functionalities, such as negative refractive [8, 9], a perfect lens [10]. Subsequently, the concept of metamaterials has been extended to acoustic and elastic systems derived from multiple scatterings in periodic structures [11–14] or local resonances of subwavelength unit cells [15–17]. Among the examples, the advent of elastic metamaterials with topological properties [18, 19] has provided a novel and effective framework for manipulating elastic transport dynamics and has become a new focus in the solid-state elastic world.

Topology is a branch of mathematics dedicated to studying the quantities that are preserved under continuous deformation. The concept of topological physics originated from the exciting discovery of the integer quantum Hall effect (IQHE) in condensed matter physics. In 1980, von Klitzing found that a two-dimensional (2D) electron gas in extremely low temperature and a strong magnetic field has a quantized Hall conductance [20]. Soon after, Thouless et al proposed that the Hall conductivity exhibits the extremely robust quantization characteristics when the time-reversal (T) symmetry is broken, which is related to a nonzero topological invariant of the system [the Chern number or Thouless–Kohomoto–Nightingale–den Nijs number [21]]. These phenomena put forward a new classification paradigm based on the notion of topological order [22, 23], which is fundamentally different from the previous understanding that phases of matter are characterized by spontaneous symmetry breaking at phase transitions [24], thereby opening up a new research field.

Over the past few years, topological phases and topological phase transitions of matter have been extensively developed in condensed matter physics owing to their fundamental characteristics that are insensitive to continuous perturbations of material parameters. Meanwhile, a class of metamaterials with nontrivial topological properties, namely, topological metamaterials, has also attracted intense research interests. The most peculiar feature of topological metamaterials [25, 26] is that they can support the gapless edge states which are absent in normal insulators. The gapless edge states can be classified into two major categories. There are chiral edge states in Chern insulators with broken T symmetry, which propagate in one direction only along the edge. There are also helical edge states in quantum spin Hall phase or edge states in quantum valley Hall phase, which are protected by T symmetry and other spatial symmetries, and support the counter-propagation at the interface between materials with different topological invariants. These two types of topological edge states are localized at the boundary and go through the topological bandgap in momentum space according to the bulk-edge correspondence [27–29]. These properties are topologically protected and enable them being immune against structural defects and disorder, thus resulting in robust propagation of the edge states along arbitrary boundaries but forbidding propagation in the bulk.

Parallel to the development of topological phases in quantum condensed matter systems, the research about topological metamaterials in classical wave systems has become one of the most active areas. In 2008, Haldane and Raghu realized a direct electromagnetic analogue of the 'chiral edge states' of electrons in the 2D periodic structure of time-reversal-breaking magneto-optical elements [30]. And they predicted that such photonic systems could support robust chiral states propagating along the boundary of the system. This sparked a series of explorations on classical applications of topological physics, especially in various kinds of wave phenomena, from photonics [31–43], to phononics [44–57] and mechanics [62–116, 121–157, 169–176, 184–190]. Compared to their fermionic counterparts, classical wave systems can benefit from their larger scale in both space and time, providing a simpler and more accurate platform for designing, fabricating and detecting various topological effects that may not be directly observed in electronic systems. However, emulating many of the key condensed matter manifestations of topological electronics to the fields of photonics and phononics might not be straightforward, because photons/phonons do not possess a half-integer spin of electrons and cannot directly interact with magnetic fields. Realizing the photonic/phononic topological phases based on the breaking of T symmetry requires additional efforts [34, 35, 45–48]. Moreover, the fundamental difference between fermionic and bosonic systems also provides a new perspective for exploring the topological phases of matter, which may have promising applications in topological photonic/phononic devices, such as low loss waveguides and sensors. In particular, the booming interest in elastic wave manipulation in the past few decades using elastic metamaterials has facilitated topological phononic band engineering. In comparison with photonic/fluid acoustic systems, elastic wave motion in solid media has richer polarization degrees of freedom (longitudinal and transverse modes) [223] that can be leveraged to construct pseudospins to mimic electronic spin states. Additionally, elastic phonons simultaneously possess several unique advantages of phononic information processing, including scalability toward integrated devices, antijamming capability, energy capacity, and extremely low losses. Therefore, topological elastic metamaterials promise to offer robust designs and unrivalled functionalities for manipulating elastic wave propagation by providing immunity to backscattering induced by 'non-magnetic' defects and fabrication imperfections. It is of great practical value to realize elastic topological states, especially in elastic waves devices that can be scaled accordingly for future chip-scale applications.

In this paper, we review the research efforts that focus on the topological elastic metamaterials and discuss various mechanisms underlying these topological phases in elastic systems. This review is organized as follows. In section 2, we introduce the basics of topological band theory starting from the one-dimensional (1D) topological elastic metamaterials, which includes the realization of the so-called Su–Schrieffer–Heeger (SSH) model in various elastic wave platforms. In section 3, we elaborate the main breakthroughs of the analogue quantum Hall effect (QHE) and quantum spin Hall effect (QSHE) in 2D elastic systems, followed by the development of quantum valley Hall effect (QVHE). Section 4 gives a brief introduction about three-dimensional (3D) elastic topological phases in topological semimetals and topological insulators (TIs). Section 5 is devoted to elastic analogue of higher-order TIs. The last section summarizes a few important technology-oriented applications of topological elastic metamaterials, and provides our perspectives on future research directions in this promising field.

We start our discussion about 1D topological phases by considering the SSH chain in electronic systems [58], in which the tight-binding model is used to describe the electronic transport in conductive polymers and provides one of the simplest lattice models with topological properties. The model consists of a 1D discrete chain of atoms with alternating hopping parameters, t and s, between nearest neighbors. The unit cell for the SSH chain includes two atoms coupled to each other with an intra-cell hopping parameter t, whereas an inter-cell hopping parameter s couples adjacent unit cells. The Hamiltonian matrix of the momentum space in the 1D system can be written as [59]

$$\begin{equation}H(k)=\left(\begin{matrix}\hfill 0\hfill & \hfill t+s\enspace {\mathrm{e}}^{-\mathrm{i}k}\hfill \\ \hfill t+s\enspace {\mathrm{e}}^{\mathrm{i}k}\hfill & \hfill 0\hfill \end{matrix}\right),\end{equation} \tag{ 1 }$$

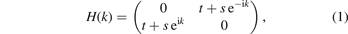
where k is the Bloch wavenumber. When t = s, the two dispersion bands of this system cross each other at the edge of the Brillouin zone (BZ), forming a topological transition point. For t ≠ s, the band structure is gapped, resulting in an insulating phase, which can be characterized by the Zak phase [60]. For a 1D periodic system, the Zak phase is defined as [61]

$$\begin{equation}{\varphi }_{\mathrm{Z}\mathrm{a}\mathrm{k}}=\frac{1}{2}\oint \frac{\partial \phi (k)}{\partial k}\enspace \mathrm{d}k,\end{equation} \tag{ 2 }$$

where the phase ϕ(k) is given by $\mathrm{cot}\enspace \phi (k)=\frac{t/s}{\mathrm{sin}\enspace ka}+\mathrm{cot}\enspace ka$. As the unit cell possesses inversion symmetry with respect to its center, the Zak phase takes the quantized values π (in the nontrivial case, t < s) or 0 (in the trivial case, t > s). As a consequence, there exist a topological interface state in the middle of the bandgap when connecting two semi-infinite SSH chains with different Zak phases. These states are localized at the interface between two lattices and decay exponentially into the lattice termination, at a rate determined by the size of the bandgap. Note that these interface modes are robust to any defects and perturbations that preserve the chiral symmetry and are not strong enough to close the bandgap.

Considering the simplicity and universality of the SSH model, this 1D topological system has been implemented in various elastic wave platforms [62–81]. For instance, Huang et al [77] realized the elastic analogue of the SSH chain in a 1D shear horizontal (SH) guided wave system, which consists of two semi-infinite solid phononic crystal (PC) plates with different Zak phases, connected to each other to form the topological interface modes at the zone-center band gap, or at the zone-boundary band gap, or both. Figure 1(a) illustrates the schematic diagram of the SSH structure and the corresponding transmission spectrum of the multi-frequency topological interface states. Chaunsali et al [78] experimentally demonstrated the SSH model in a highly tunable mechanical system made of cylindrical granular particles. By changing the contact angles between the cylinders, the interparticle stiffness can be tuned, thereby giving rise to a nontrivial topological phase. Figure 1(b) shows a topological band transition process of three dimer configurations of the infinite dimer chain, which manifests as the emergence of the topological edge mode in the system. Another strategy to realize the actively tunable topological protected interface mode is to employ step-wise open-closed periodic electrical boundary conditions (EBCs) in a 1D homogeneous piezoelectric rod system (see figure 1(c)) [79]. Subsequently, Wang et al [80] realized a topological Fano mechanical resonance by engineering band inversion of two different vibrating symmetries of a pillared phononic beam that gives rise to topological dark and bright edge modes (see figure 1(d)). The SSH model has also been implemented in nonlinear elastic system. Vila et al [81] reported on the effect of nonlinearities on topological protection in a 1D mechanical lattice composed of an array of spinners coupled through permanent magnets. Nonlinearities induced by increasing amplitude of motion cause the topologically protected interface modes to shift and merge with the bulk bands, as shown in figure 1(e). In addition to the SSH-type lattices, quasicrystal structures were also investigated by implementing the 1D Fibonacci chain [82, 83]. Zhao et al [83] demonstrated the existence of multiple interface states of SH guided waves in 1D phononic quasicrystal slabs constructed by Fibonacci sequence chains (see figure 1(f)).

Zoom In Zoom Out Reset image size

The strong localization characteristics of the topological interface modes in 1D elastic systems have potential applications where strong vibration intensities are required, such as high-sensitivity signal sensing [219], vibration isolation [82], energy harvesters [220], and biomedical imaging [222]. However, these interface modes cannot be used for waveguiding, as they are confined in zero dimensions. In the next section, we move to discuss 2D topological metamaterials whose edge modes are localized in one dimension and can therefore be leveraged for waveguiding and energy transport.

3.1. Elastic analogues of quantum Hall effect

The QHE provided the first realization of the 2D topological phases of matter. In quantum mechanics, the IQHE is obtained by applying an external magnetic field in 2D electron gas systems [20] with broken T symmetry, in which the electrons flow unidirectionally along the edges without backscattering or dissipation. The associated Hall conductance takes the quantized values σ_H = Ce²/h, where h is the Plank constant, e is the electron charge, and C is an integer, corresponding to the topological invariant of the system. For the 2D system, the Chern number is defined as a surface integral over the BZ, which can be given by [21]

$$\begin{equation}C={\frac{1}{2\pi }\oint }_{\mathrm{B}\mathrm{Z}}F(\boldsymbol{k})\mathrm{d}\boldsymbol{k},\end{equation} \tag{ 3 }$$

where F( k ) = ∇ _k × A( k ) is the Berry curvature and $A(\boldsymbol{k})=\left\langle {\mu }_{n}(\boldsymbol{k})\right\vert \mathrm{i}{\nabla }_{\boldsymbol{k}}\left\vert {\mu }_{n}(\boldsymbol{k})\right\rangle$ is the Berry connection. μ_n ( k ) represents the periodic part of the corresponding Bloch state on the nth band, k is the Bloch wavenumber, and ∇ _k is the curl operators with respect to k . When the system breaks the parity-inversion (P) symmetry but preserving the T symmetry, the Berry curvature is an odd function of k , F( k ) = −F(− k ), and the Chern number equals to zero. In contrary, in the presence of the P symmetry (the T symmetry broken), the Berry curvature is an even function of k , F( k ) = F(− k ), and the Chern number is nonzero. Nonzero Chern number corresponds to a nontrivial insulating phase while zero Chern number corresponds to a trivial insulating phase. The topological phases with nonzero Chern number support a gapless edge state in the bulk energy gap, exhibiting unique unidirectional charge transport and robustness against impurities.

Motivated by the developments of quantum Hall phases in electronic systems, such phases were transferred to the classical realms [34, 35, 45–48, 84–87] shortly thereafter. The first theoretical [34] and experimental proposals [35] of analogue QHE in photonic systems were realized at microwave frequencies. They broke the T symmetry by applying a uniform magnetic field on gyromagnetic photonic crystals, resulting in one-way topologically protected edge states that propagate around defects without backscattering. However, acoustic and elastic waves are magnetically inert. Breaking the T symmetry in these systems demands new approaches, such as using magneto-acoustic materials or introducing nonlinearity. In acoustics, Fleury et al [45] proposed a feasible method to break the T symmetry by generating circulating air flow in a linear and magnetic-free circulator to mimic a magnetic bias, thus inducing nonreciprocity of airborne sound waves. To obtain the elastic analogues of quantum Hall phases, an efficient scheme is to utilize the chiral nature of gyroscopes [84]. This achievement was obtained in 2D hexagonal lattice consisting of gyroscopes with the top tip pinned to a mass, as shown in figure 2(a). The introduced gyroscopic inertial effect breaks the T symmetry and leads to a topologically nontrivial bandgap (see figure 2(b)). Nash et al [85] experimentally demonstrated a gyroscopic metamaterial consisting of a honeycomb lattice in which the masses are replaced by gyroscopes with the neodymium magnets (see figure 2(c)). In the magnetically coupled system, the T symmetry is broken by the fast spinning of the gyroscopes. These one-way chiral edge modes are topologically protected and thus immune to disorders, as illustrated in figure 2(d). A further study indicated that this system can give rise to a complex band topology by introducing a tunable spindle lattice of gyroscopes [86]. These topological modes are determined by the competition between T symmetry and site equivalence. In another approach, Wang et al [87] proposed a simple 2D classical mechanical system with honeycomb mass-spring lattice positioned in a rotating frame as shown in figure 2(e). It was proved that the Coriolis force induced by the non-inertial reference frame can be regarded as a uniform effective magnetic field, thereby giving rise to a topologically nontrivial state (see figure 2(f)).

Zoom In Zoom Out Reset image size

3.2. Elastic analogues of quantum spin Hall effect

In addition to the QHE that requires the T symmetry breaking, there exists another type of 2D topological phases protected by the T symmetry, which typically occurs in the presence of spin–orbit coupling, as in the QSHE [88, 89]. This quantum spin Hall state can be regarded as two time-reversed copies of the quantum Hall state with opposite Chern numbers for each spin. As a consequence, the systems support two helical edge modes that propagate along the boundaries in opposite directions, carrying spin-up and spin-down electrons. This spin-momentum-locked propagation is robust and cannot be backscattered at non-magnetic defects if the spin is not flipped. However, realization of these quantum hall phases in classical realms is not quite straightforward. Owing to the intrinsic spin-1/2 fermionic property of electrons, the time-reversal operation satisfies ${{T}_{\mathrm{f}}}^{2}=-1$, which guarantees the Kramers degeneracies at the time-reversal-invariant points. By contrast, photons/phonons are spin-less particles and belong to spin-1 bosons, for which the time-reversal operator obeys ${{T}_{\mathrm{b}}}^{2}=1$, and have no counterparts of two degenerate modes in the spin degree of freedom. Therefore, to realize the equivalent of the QSHE in classical systems, it is necessary to construct a pseudospin degree of freedom and pseudo T symmetry with another symmetry operation ς such that ${(\varsigma {T}_{\mathrm{b}})}^{2}=-1$, enforcing Kramers degeneracy when both ς and T_b are preserved [37–39, 50–53, 90–116].

Constructing artificial Kramers pairs in elastic systems, referred to as elastic pseudospins ±1/2, is not an easy task. The first realization of the elastic analogue of QSHE was made in a mechanical oscillator system [107], in which the local Kramers pairs are formed by the polarization of the coupled 1D pendulums. Similar strategy to emulate mechanical spin states is to utilize the rotations of a particle with left/right circular polarizations in a granular grapheme system [108]. In another work, Mousavi et al [109] proposed a modified dual-scale PC slab to realize topologically protected helical edge modes. Double Dirac cones is formed based on accidental degeneracy between the symmetric (S) and anti-symmetric (A) Lamb modes. By breaking the σ_z mirror symmetry, elastic spin–orbit coupling is introduced to mimic two effective spins, accompanied by the opening of the complete topological bandgap at the K point, as shown in figure 3(a). Inspired by this work, helical edge states were experimentally implemented in elastic plates patterned with triangular holes [110], in which the σ_z mirror symmetry is broken by the drilling of blind holes on one side (see figure 3(b)). Meanwhile, Yu et al [111] experimentally demonstrated an elastic analog of the QSHE in a monolithically scalable configuration consisting of order-perforated plates with different hole-center distances. The elastic pseudospins ±1/3 with spin-momentum locking are constructed through the modal hybridization between the S and A modes. As illustrated in figure 3(c), the obtained helical edge states are robust against various defects and exhibit nearly a loss-free elastic transport along the topologically protected waveguide (TPWG). Another approach was proposed using the zone-folding strategy [38], instead of polarization or modal hybridization, to create the elastic pseudospin states. For example, Huo et al [112] investigated a 2D solid/solid hexagonal-latticed phononic system that simultaneously supports the topologically protected edge states for out-of-plane and in-plane bulk elastic waves. By expanding a primitive unit cell to a larger cell, the two-fold Dirac cone at the K point in the original BZ are folded at the Γ point in the new BZ, forming a double Dirac cone with four-fold degeneracy. This strategy has been successfully implemented on the microscopic scale [113, 114]. As shown in figure 3(d), Cha et al [114] reported the experimental realization of on-chip topological nanoelectromechanical metamaterials, consisting of 2D free-standing silicon nitride nanomembranes with extended honeycomb lattice that operate at high frequencies (10–20 MHz). In our group, an elastic TI has been experimentally realized based on a topological modification in a triangular lattice of elliptical cylinders [115], in which multiple topological transitions for in-plane bulk waves are induced by inhomogeneously changing the ellipse orientation within the unit cells. The solid PC system exhibits the spin-locked edge modes that support robust one-way propagation along channels with sharp bends (see figure 3(e)), allowing for a flexible geometric configuration beyond the point-group symmetry. Further study [116] demonstrated that this pseudospin-Hall PC can be effectively described as an elastic near-zero refractive index metamaterial, which can achieve the defect-immune topological zero refraction with arbitrary angles of incidence and wide working frequency range (see figure 3(f)). Such a flexible platform enables the simultaneous control of the refraction properties of longitudinal and transverse waves and has potential applications in topological elastic antennas and elastic wave collimator.

Zoom In Zoom Out Reset image size

3.3. Elastic analogues of quantum valley Hall effect

The discrete valley degree of freedom or valley pseudospin [117], labeling quantum states of energy extrema in momentum space, has been extensively studied in condensed matter physics because of its potential as a new type of information carrier and its application prospect in valleytronics [118, 119]. In a hexagonal crystal lattice, there exists a pair of degenerate states at the inequivalent K and K' valleys of the BZ. The breaking of inversion symmetry lifts the Dirac degeneracy at a valley and produces valley-Hall TIs [120], in which valley-chiral electrons propagate along the boundaries in the opposite directions. In the quantum valley Hall system, the topological invariant can be calculated by replacing the BZ in equation (3) with the half of the BZ around the valley, which is called the valley Chern numbers. Along the interfaces between two medias with distinct valley Chern numbers, this valley-momentum locking characteristic enables edge transport robust against defects that do not cause intervalley scattering.

Recently, the concept of valley pseudospin can also be transferred to elastic wave realms [121–157]. An effective strategy to emulate the QVHE in elastic systems is to utilize spring-mass resonators to produce opposite polarizations [150–152]. Pal and Ruzzene [150] leveraged the valley degree of freedom to realize the elastic analogues of the QVHE on an elastic hexagonal-latticed plate featuring an array of resonators. Broken inversion symmetry while preserving C₃ symmetry is achieved by introducing a mass difference between the two resonators within the unit cell, and a topologically nontrivial bandgap emerges at the K point, as shown in figure 4(a). As a consequence, the system exhibits backscattering suppressed valley edge modes at the interface between two topologically distinct lattices. Furthermore, our research [151] showed that by simply tuning the height of stubs (resonators) deposited on the elastic thin plates, the inversion symmetry can be broken, giving rise to the topologically protected valley transports of plate-mode waves. Another approach was proposed to construct valley pseudospin in elastic kagome lattices by changing the spring constants k instead of the masses [152]. Elliptical polarization with opposite handedness can be produced by varying contrast β ≡ (k₁ − k₂)/(k₁ + k₂), which guarantees that two topologically distinct kagome lattices support in-plane topological Stoneley waves propagated along their interfaces. Meanwhile, Li et al [153] reported a concept of valley anisotropy by designing asymmetrical elastic metamaterials made of hard spiral scatterers and soft material matrix (see figure 4(b)). The introduced asymmetrical structure without inversion symmetry enables topological manipulation of transverse elastic waves, allowing bending and stoppage of energy flow. In another work, the strain field was introduced to realize a tunable topological elastic phononic waveguide [154]. The space-inversion symmetry breaking is induced by producing elastic deformations of the trusslike hexagonal lattice, which opens up an incomplete bandgap of flexural waves, as shown in figure 4(c). The obtained valley edge states can be tailored efficiently by simply tuning the pressure within the unit cells. This quantum valley Hall states have also been implemented in a 2D elastic hexagonal lattice with added masses at the sublattice sites (see figure 4(d)) [155]. Subsequently, Yan et al [156] experimentally realized the gyral valley states and valley edge transport on silicon chips patterned with a 2D hexagonal array of triangular pillars. The mirror symmetry is broken by tuning the rotation angles of the triangular pillars, resulting in valley edge states of the Lamb waves at the topological channel between distinct valley Hall phases, as displayed in figure 4(e). Recently, Huang et al [157] proposed a ternary valley-Hall PC with the complex lattice to realize topological negative refraction of in-plane waves at the deep subwavelength scale. As shown in the right panel of figure 4(f), by inhomogeneously changing the elliptical cylinder orientation, a band inversion can occur near the resonance frequency, thus generating the valley polarized edge modes induced by locally resonant state.

Zoom In Zoom Out Reset image size

Parallel to the development of 2D topological metamaterials, recently intensive research effort has been devoted to explore new topological phases by using a 3D structure that consists of unit cells periodically arranged along all three spatial directions. These 3D topological phases including topological nodal lines [158–160], Weyl points [161–166], and TIs [167, 168], manifest the gapless surface states that support robust edge transport against defects along any spatial direction without being constrained by a certain plane. Weyl points are particularly interesting as they serve as sources or sinks of Berry flux, carrying a quantized topological charge of ±1, which requires breaking either T symmetry or P symmetry. The associated topological charges explain that the Weyl points are robust any perturbations and they can only be annihilated by merging oppositely charged pairs. Another intriguing topological feature of Weyl points is the existence of a Fermi arc between a pair of Weyl points, which corresponds to nontrivial surface states along any surface interface according to the bulk-surface correspondence.

Despite the fact that Weyl semimetals have successfully been demonstrated in photonics [161, 162] and fluid acoustics [163–166], the realization of such topological semimetal phases is quite challenging for elastic systems due to the complicated coupling and conversion of various elastic wave modes, as well as the difficulty in 3D solid material manufacturing. Up to now, only a few studies on elastic Weyl points have been reported [169–173]. The study by Wang and Tsai [171] proposed a chiral beam-plate structure through stacking of a 2D honeycomb elastic lattice, which carries multiple Weyl and double-Weyl points. The Weyl points with ±1 (2) charges guaranteed by specific symmetries bring about topologically nontrivial surface modes, in which the flexural wave propagation is robust against a sharp corner without reflections. Later, Shi et al [172] realized an elastic analog of Weyl semimetal based on AA-stacked honeycomb lattice made of slender beams, as shown in figure 5(a). This 3D hollow structure with chiral interlayer hopping carries elastic Weyl points with opposite topological charges (±1) (see figure 5(b)) and elastic Fermi arcs (see figure 5(c)). The associated gapless topologically protected surface states display the collimation effect of the propagating elastic waves and the robust one-way transport behaviors of elastic energy around the defects. Another study by Ganti et al [173] discussed the possibility to achieve Weyl semimetals based on a fully continuous and load-bearing design. Figure 5(d) represents the corresponding 3D sandwich composite structure, consisting of a layered prismatic lattice with hexagonal cross sections in which the layers are spaced by solid cylindrical elements and the consecutive faces of the prismatic unit cell are connected by slanted circular beams. The breaking of the mirror symmetry and P symmetry of the lattice guarantee the existence of Weyl points at K and H points, as shown in figure 5(e). The obtained surface states exhibit the extreme robustness toward lattice disorder and defects (see figure 5(f)). Besides, the topological nodal lines have been proposed in 3D mechanical metacrystals of tetragonal symmetry [174]. The resultant ribbon- or drumhead-like surface states enable strong subwavelength confinement of elastic waves with suppressed group velocity and exhibit unusual frequency stability against perturbations.

Zoom In Zoom Out Reset image size

In addition to the 3D gapless phases, there is another type of phase among 3D topological phases, i.e., the 3D gapped topological phases, also known as the 3D TIs [167, 168, 175, 176]. Such phases are attributed to the 3D topological band gap that hosts gapless surface states localized at all three spatial directions, in contrast to 2D TIs, in which the edge states are confined in a 2D plane. For 3D elastic systems, the topological insulating phases are more complex but more attractive than those for 2D systems. Huo et al [175] experimentally realized a 3D elastic TI based on the stacked plate-like metamaterials (see figure 5(g)). In this system, the 2D valley surface states along the 2D projected plane are obtained in 3D monolayer-stacked structure without interlayer coupling. By stacking the monolayer into bilayer with a twisted angle of 60°, the interlayer mirror symmetry and in-plane inversion symmetry are simultaneously broken, which introduces the non-zero interlayer coupling of elastic valley layer, thus giving rise to the 2D topological layer-dependent surface states, as illustrated in figure 5(h). The obtained valley and layer-dependent surface states support the robust and layer-selective transports of 3D elastic wave with the backscattering immunity against the straight channel and sharp bends (see figure 5(i)). This might have potential applications in high-dimensional elastic wave devices, such as 3D layer-selective waveguide and splitter.

The topological insulating phases discussed thus far have an insulating bulk with gapless boundary modes, which are one dimension lower than the bulk. In other words, a d-dimensional TI possesses d-dimensional gapped bulk states and (d − 1)-dimensional gapless boundary states. Recently, a new class of topological phases, called higher-order TIs, has been proposed in condensed matter physics. These higher-order topological phases exhibit topologically nontrivial boundary modes that are more than one dimension lower than the bulk, which do not obey the traditional bulk-boundary correspondence. Generally speaking, a d-dimensional nth-order TI supports (d − 1)-, (d − 2)-, ..., (d − n + 1)-dimensional gapped boundary states and d − n dimensional gapless boundary states. For example, a second-order TI in 2D lacks topologically protected gapless 1D boundary states, but instead exhibits zero-dimensional (0D) gapless corner states that are localized at the 'boundaries of boundaries', that is, at the corners of the insulator.

With the development of higher-order TIs in electronics [177, 178], photonics [179, 180] and airborne acoustics [181–183], the topological insulating phases have also been transferred to elastic systems [184–189]. Serra-Garcia et al [187] first experimentally realized an elastic analogue of 2D quadrupole TI based on perturbative mechanical metamaterials consisting of single-crystal silicon plate (see figure 6(a)). In their setting, the thin beams between the nearest neighboring plates control the sign and amplitude of the corresponding coupling coefficients λ and γ, which can lift the bandgap between two pairs of degenerate bands and thus produce the nontrivial insulating phase. Figure 6(b) shows the spectral response of bulk (blue), edge (orange), and corner (green) modes, when the nontrivial structure is excited with an ultrasound air-transducer. Figure 6(c) depicts the spatial profile of in-gap corner states, demonstrating their confinement to the corners of the plate. Motivated by the Wannier-type corner states in the breathing kagome lattice in acoustic structures [181, 182], a similar experimental observation was conducted on the in-plane dynamics of second-order TI in a mechanical kagome lattice [188]. The corresponding kagome lattice is shown in figure 6(d), consisting of the thin disks of equal radius r interconnected by the bivalued widths of bars. The intracouplings and intercouplings between sites can be tuned by shrinking the width of bars, thus leading to the in-gap higher-order corner states. Figure 6(e) represents the normalized energy spectra for bulk (P1), edge (P2), and corner (P3) states. As illustrated in figure 6(f), the experimentally measured mode shapes confirm the occurrence of the corner state in this lattice. Such 0D corner states hold great promise for controlling and trapping in-plane waves at specific points in a robust fashion, which provides the possibility of practical application in energy harvesting devices. The Jackiw–Rebbi soliton mechanism has been proposed to host topological corner modes without requiring negative coupling. Huo et al [189] demonstrated an elastic second-order TI based on a square lattice consisting of perforated plate with double-side pillars (see figure 6(g)). The inversion symmetry is broken by changing the width of two neighbor pillars, and the band inversion is induced by emulating the QHSE through the zone-folding strategy. Shown in figure 6(h) is the calculated spectrum of bulk, edge, and corner states in a box-shaped structure, from which an additional four cracked corner states appear in the gap of the edge states in contrast to previous second-order TI realizations in acoustics [183]. It can be seen from the displacement field distributions in figure 6(i) that the corner states are indeed localized at the four corners of the crystal.

Zoom In Zoom Out Reset image size

In this article, we have presented a brief review of the recent advances in the field of topological elastic metamaterials. Starting from the topological band theory, different implementations of elastic topological phases with unique topological invariants were discussed, including elastic SSH model in 1D, QH/QSH/QVH-like states in 2D, elastic Weyl points, nodal lines, and TIs in 3D, and higher-order elastic topological phases. In analogy with topological phenomena in condensed matter physics, its elastic analog has attracted particular research interests because elastic phonons possess richer polarization degrees of freedom compared with photons/airborne phonons. The findings of more topological elastic metamaterials not only deepen our understanding of various elastic topological states but also provide a robust platform for research into elastic transport dynamics to spearhead novel elastic wave physics. To date, plenty of unknown phenomena and mechanisms in topological elastic systems, as well as their technology-oriented applications, remain to be explored. In future studies, several challenges and possible research directions in this field should be focused.

While most of topological phases discussed thus far are based on linear structure, combining these topological structures with nonlinear effects is a particularly promising field due to the prevalence of nonlinearity in the physical world. Currently, there is a plethora of theoretical predictions and experimental demonstrations of nonlinear phenomena in topological electronics, photonics and acoustics, including bulk solitons emerging from topological bands [191], topological laser [192], and nonlinearly induced topological edge states [193]. For elastic systems, the bulk-boundary correspondence involved in the nonlinear process and the inherent relationship between the nonlinear output of the system and the global topological invariant remain elusive.

In addition to topological nonlinearity, another promising multiphysics platform is based on non-Hermitian systems [194–201]. Recently, non-Hermitian topology has been studied to reveal many unconventional topological functionalities, features, and phenomena, such as non-reciprocal propagation [195], modified bulk-boundary correspondence [196], feedback control interactions [197, 198], exceptional points [199], and non-Hermitian skin effect [200, 201]. Similar to quantum mechanical systems, the interplay between gain and loss in classical mechanical systems makes elastic energy non conservative, thus giving rise to the dynamical matrix being non-Hermitian. However, due to the practical difficulties in introducing gains and losses into elastic systems, the realization of non-Hermitian elastic topological phases is still challenging.

Looking further ahead, exploring topological phases in dimensions higher than the apparent geometrical dimensionality of the structures [202–213] is another promising direction of research. The initial motivation for pursuing such higher topological phases is to develop a versatile approach in acoustic and elastic media for demonstrating many important topological physics effects. For instance, topological edge modes reminiscent of 2D QHE systems have been successfully realized in 1D quasiperiodic systems with additional parameters [82, 202–205], which can be employed to engineer topological pumps [206–210]. In particular, there have been several recent reports on topological phases in four dimensions and above, based on the concept of synthetic dimension [211, 212]. A typical example is employ 2D phononic lattices with modulated properties to realize four-dimensional QHE via simple twisting and sliding [213]. In general, the idea of utilizing synthetic dimension to search for new phases of elastic topological states appears to be very rich and not yet fully exploited. Besides, some newly emerged concepts, such as, topological Anderson insulators [214], topological quasicrystals [215] and amorphous systems [216] remain mostly unexplored in classical elastic systems.

Along with the academic research on realizing and demonstrating elastic topological phases, it is of substantial significance to implement the technological-oriented application of topological elastic metamaterials. For example, realizing defect-immune waveguiding, signal buffering and beam splitting could provide new insights for improved elastic waves sensors [217], antennas [218], signal processing [219], and energy harvesting [220]. In particular, the rapid development in advanced manufacturing techniques, especially 3D printing, has enabled the fabrication of intricate features at various length scales. As a result, it will become easier to design and manufacture multi-scale elastic metamaterials with topological properties, which promotes the application in the realm of both practical elastic device engineering and fundamental physics, such as vibration isolator [82], on-chip transducers [114], or antifracture materials [221].

Overall, while many of the breakthrough findings reviewed in the context of topological elastic metamaterials have been motivated by physics-driven explorations, the emerging field has a bright future not only based on purely theoretical research, but also as unprecedented routes and possibilities for phononic technologies that fully take advantage of topologically robust elastic wave control.

The authors gratefully acknowledge financial support from National Science Foundation of China under Grant No. 12074114 and the Foundations of Hubei Key Laboratory of Hydroelectric Machinery Design and Maintenance of China Three Gorges University under Grant No. 2019KJX02.

No new data were created or analyzed in this study.