Abstract
We study the energy and creep velocity of magnetic domain walls in perpendicularly magnetised Pt/Co/Ir thin films under strain. We find that the enhancement of domain wall creep velocity under strain from piezoelectric transducers is largest in films with the thinnest Co layers (0.56 nm), in which the strain causes the smallest relative change in perpendicular magnetic anisotropy and the largest relative change in domain wall creep velocity. We show how domain wall energy is predictive of the sensitivity of domain wall creep velocity to changes in strain, and thus provide a route to designing magnetic thin film systems for optimum strain control.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The application of strain to a magnetostrictive ferromagnet gives a degree of control over the magnetic anisotropy energy of the material. In recent years there has been interest in controlling perpendicular magnetic anisotropy in thin films via strain from a piezoelectric material [1–4] and we have previously demonstrated control over the creep velocity of domain walls using strain in Pt/Co/Pt thin films [5]. Here we study the balance of anisotropy and exchange energy terms by investigating how the magnetic domain wall energy is affected by both magnetic layer thickness and externally applied strain in Pt/Co/Ir thin films.
We use strain from a piezoelectric transducer to modify the perpendicular magnetic anisotropy energy of Pt/Co/Ir thin films with a range of Co thicknesses. We show how the consequent change in domain wall energy relates to the measured change in domain wall creep velocity as a function of strain. In particular, an increase in the creep velocity of domain walls in Pt/Co/Ir cannot be understood simply from the amount by which the magnetic anisotropy is modified by strain, but does correlate well with the change in domain wall energy. We show that by knowing the energy of magnetic domain walls, we can better understand the velocity changes in Pt/Co/Ir thin films tuned by Co thickness and strain from a piezoelectric material.
2. Experimental details
We investigated the effect of strain on the domain wall energy and creep velocity using piezoelectric transducers. Thin glass substrates with Pt/Co/Ir thin films on top were bonded to biaxial piezoelectric transducers with epoxy resin. Voltages of between −30 and 150 V can be applied to the transducers to strain the thin films by up to 0.1% [5]. A positive voltage corresponds to a tensile out-of-plane strain and isotropic in-plane compression. The maximum applied strain causes a 10 kJ m−3 reduction in the perpendicular magnetic anisotropy, which is consistent with the anisotropy change for Pt/Co/Pt thin films [5].
We measured the domain wall creep velocity of a series of thin films of Ta(4.5 nm)/Pt(4 nm)/Co(t)/Ir(5 nm), with Co thickness t of 0.56, 0.67, 0.78 and 0.89 nm, deposited onto thin glass substrates by dc magnetron sputtering [6]. Domain wall creep velocities were measured using wide-field Kerr imaging. To measure a velocity, the film was saturated, then a field pulse was applied to nucleate a reverse domain. A second field pulse was applied to move the domain wall and expand the reverse domain. The difference between images of the nucleated and expanded domain gives the distance travelled during the second field pulse.
The magnetic properties of the thin films were characterised using superconducting quantum interference device vibrating sample magnetometry (SQUID-VSM). The magnetisation and perpendicular magnetic anisotropy were measured from in-plane SQUID-VSM hysteresis loops. The exchange stiffness was measured by fitting saturated magnetisation versus temperature curves to a Bloch T3/2 law [6–8]. The interfacial Dzyaloshinskii–Moriya coefficient was estimated using the creep method [9] with asymmetric expansion of domains under in-plane bias fields. The velocities of domain walls travelling under a fixed out-of-plane driving field are measured parallel and antiparallel to an in-plane bias field. The positions of the minima of these curves give an estimate of the bias field needed to balance the DM field that acts within a non-Bloch domain wall. The DM coefficient can be calculated from the DM field [10, 11] using
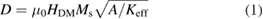
where HDM is the DM field, Ms is the saturation magnetisation, A is the exchange stiffness and Keff is the effective perpendicular magnetic anisotropy.
3. Results and discussion
We first measure the domain wall creep velocity in perpendicularly magnetised Pt/Co/Ir under out-of-plane driving fields Hz. Domain wall velocity in the creep regime [12] is given by
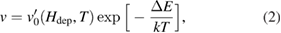
where  is a velocity scaling parameter that can vary as a function of depinning field and temperature, k is the Boltzmann constant, T is the temperature and the universal creep energy barrier scaling parameter is
is a velocity scaling parameter that can vary as a function of depinning field and temperature, k is the Boltzmann constant, T is the temperature and the universal creep energy barrier scaling parameter is
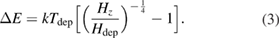
We can write the equation in a linear form
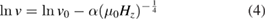
where the intercept is  and the gradient is the energy barrier scaling parameter
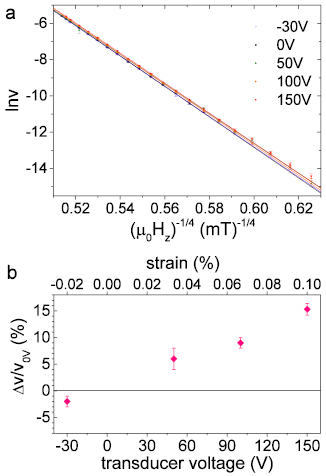
and the gradient is the energy barrier scaling parameter  . The linear fits of equation (4) to the velocity data in figure 1(a) show that the domain wall motion that we measure in Pt/Co/Ir is in the creep regime.
. The linear fits of equation (4) to the velocity data in figure 1(a) show that the domain wall motion that we measure in Pt/Co/Ir is in the creep regime.
Figure 1. Domain wall creep velocities in Pt/Co(0.89 nm)/Ir are shown for a range of transducer voltages between −30 V and 150 V. (a) The natural logarithm of the velocities is plotted over a range of out-of-plane driving fields. (b) The mean relative velocities (with respect to the velocity at 0 V) are plotted against the transducer voltage.
Download figure:
Standard image High-resolution imageFigure 1(b) shows how the creep velocity changes with strain applied using the piezoelectric transducer. Tensile out-of-plane strain (from biaxial in-plane compression) at positive voltages increases the velocity at which domain walls travel in the creep regime. Figure 1(b) shows the proportional change in creep velocity  between the unstrained and 0.1% strained films, averaged over many out-of-plane driving fields and with no in-plane fields applied. In Pt/Co/Ir, the largest change in velocity is a 42% increase in the film with the thinnest Co (t = 0.56 nm, shown later).
between the unstrained and 0.1% strained films, averaged over many out-of-plane driving fields and with no in-plane fields applied. In Pt/Co/Ir, the largest change in velocity is a 42% increase in the film with the thinnest Co (t = 0.56 nm, shown later).
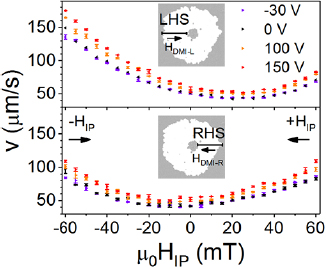
Figure 2 shows the effect of strain on the velocity versus in-plane bias field curves used to estimate DM field. The velocity increase and the slight narrowing of the curve are consistent with a lowering of the effective anisotropy and a reduction of the creep energy barrier given in equation (3). The position of the velocity minimum does not change measurably, meaning that the DM field is not significantly affected by the 0.1% out-of-plane strain.
Figure 2. Domain wall creep velocities for an out-of-plane driving field of 10.6 mT in Pt/Co(0.89 nm)/Ir are plotted against in-plane bias field over a range of transducer voltages. The top panel shows data for left-moving domain walls, the bottom panel shows data for right-moving domain walls. The inset images show domains, where the bright contrast is the region that the domain wall has moved through during an out-of-plane field pulse. The arrows show the directions of the in-plane bias fields HIP and DM fields HDM.
Download figure:
Standard image High-resolution imageThere may be a strain-induced change of the DM coefficient that is below the sensitivity of our measurements. We can estimate the effect of strain by considering a small change to D. In a study on W/CoFeB/MgO thin films, Kim et al [13] deduced a relation  , where Dat is the interatomic antisymmetric exchange energy, and d is the distance between magnetic and heavy metal atoms perpendicular to the plane. Approximating a simple cubic lattice where
, where Dat is the interatomic antisymmetric exchange energy, and d is the distance between magnetic and heavy metal atoms perpendicular to the plane. Approximating a simple cubic lattice where  [14] with lattice constant a and magnetic thickness teff, a small change due to 0.1% strain gives
[14] with lattice constant a and magnetic thickness teff, a small change due to 0.1% strain gives  . Assuming that the exchange stiffness is effected by lattice deformations in a similar way to the DM coefficient, we might expect similarly small changes in A. Changes of 0.2% are below the sensitivity of our measurements and are much less than the change in Keff (∼2%) due to 0.1% strain. We would require at least 1% out-of-plane strain to change the DM coefficient by 2%, above which we might begin to see some effect on measured values. We note that in the case of a textured polycrystalline, multilayered thin film there are many factors that influence the exchange properties. Effects from film thickness [6] and intermixing [15] may dominate over what can be estimated from simple assumptions based on lattice strains or achieved experimentally with piezo-transducer strains.
. Assuming that the exchange stiffness is effected by lattice deformations in a similar way to the DM coefficient, we might expect similarly small changes in A. Changes of 0.2% are below the sensitivity of our measurements and are much less than the change in Keff (∼2%) due to 0.1% strain. We would require at least 1% out-of-plane strain to change the DM coefficient by 2%, above which we might begin to see some effect on measured values. We note that in the case of a textured polycrystalline, multilayered thin film there are many factors that influence the exchange properties. Effects from film thickness [6] and intermixing [15] may dominate over what can be estimated from simple assumptions based on lattice strains or achieved experimentally with piezo-transducer strains.
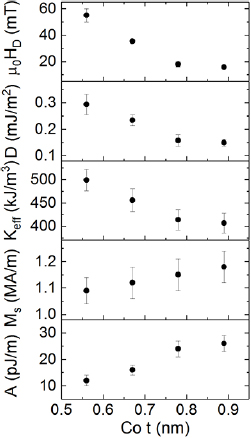
The estimated DM field and DM coefficient are plotted in figure 3 for unstrained Pt/Co/Ir with four different Co layer thicknesses, along with the perpendicular magnetic anisotropy energy, saturation magnetisation and exchange stiffness. Using the measured magnetic properties we calculate the energy of Bloch–Neél domain walls that exist where there is some DM interaction, but not enough to give a full Neél wall [9–11]. The domain wall energy is given by
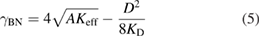
where the domain wall shape anisotropy [10, 16] is  (δ is the domain wall width). Since D is relatively small, the correction to the wall energy compared to a pure Bloch wall (which has an energy of
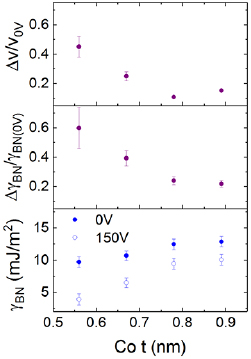
(δ is the domain wall width). Since D is relatively small, the correction to the wall energy compared to a pure Bloch wall (which has an energy of  ) is minor. The calculated domain wall energy is shown for Pt/Co/Ir at different Co thicknesses in figure 4 (bottom panel), for 0 V and 150 V.
) is minor. The calculated domain wall energy is shown for Pt/Co/Ir at different Co thicknesses in figure 4 (bottom panel), for 0 V and 150 V.
Figure 3. The measured magnetic properties (DM field, DM coefficient, magnetic anisotropy energy, saturation magnetisation and exchange stiffness) are plotted against Co thickness for Pt/Co/Ir thin films.
Download figure:
Standard image High-resolution imageFigure 4. The relative change in velocity under strain, the relative change in the domain wall energy, and the domain wall energy at 0 V and 150 V in Pt/Co/Ir are plotted against Co thickness.
Download figure:
Standard image High-resolution imageThe anisotropy reduction under strain in our Pt/Co/Ir is between 2.0% for thicker and 2.5% for thinner films. In the creep regime of domain wall motion, changing the anisotropy will modify the energy barrier to domain wall propagation. In the creep law (equation (2)) the domain wall velocity has an exponential dependence on the size of the energy barrier, so a small change of approximately 2% leads to a much larger change in velocity. As with Pt/Co/Pt [5], we find that considering only the proportional change in the magnetic anisotropy does not give a very accurate prediction of how much the creep velocity will change under strain.
For Pt/Co/Pt we previously found the domain wall creep velocity in thicker Co films to be more sensitive to strain: the percentage change in the velocity under strain increased as the film thickness increased, even though the anisotropy change was the same for different thicknesses. Here, measuring domain wall creep in thin films of Pt/Co/Ir under piezoelectric strain, we find the opposite trend with thickness, i.e. the percentage change in velocity decreases as film thickness increases.
Since the change in velocity is due to a 10 kJ m−3 reduction in magnetic anisotropy of all samples, the higher anisotropy of films with thinner Co means a lower proportional change in anisotropy. We might expect this to induce a smaller change in the energy barrier to domain wall motion, and so a smaller change in velocity, as was found in Pt/Co/Pt. However, the energy of the domain wall depends not just on the magnetic anisotropy energy, but also the exchange energies. The domain wall energy for the unstrained and 0.1% strained films can be calculated from equation (5) and is plotted in figure 4 (bottom panel), along with the proportional change in domain wall energy due to strain (middle panel). Note that, although there is a DM interaction in these films, it is not large enough to give the domain walls a Néel structure and only gives a small reduction in the domain wall energy. Using the magnetic properties from figure 3 to calculate domain wall energy, the relative size of the change of domain wall energy under strain is very close to the relative size of the change of creep velocity over the range of driving fields studied ( ). The change in domain wall velocity is due to how the change in Keff affects domain wall energy, thus the trend in Co thickness of
). The change in domain wall velocity is due to how the change in Keff affects domain wall energy, thus the trend in Co thickness of  can be understood as a balance of exchange and anisotropy terms.
can be understood as a balance of exchange and anisotropy terms.
The correlation of the changes in domain wall energy and creep velocity under piezoelectric strain show that by knowing the magnetic properties of a material with perpendicular magnetic anisotropy, we are able to properly calculate the domain wall energy and use it to predict the degree of strain control of domain wall velocity possible. To optimise strain control, we should choose magnetic thin film systems whose properties give low domain wall energies, i.e. multilayers which, as much as possible, balance low magnetic anisotropy energy, low Heisenberg exchange energy, and higher DM exchange energy.
4. Summary
We have shown that the DM coefficient in Pt/Co/Ir thin films is not significantly affected by up to 0.1% biaxial strain from a piezoelectric transducer. We demonstrate that the sensitivity of the domain wall creep velocity to strain is set by the size of the domain wall energy, which confirms the relevance of the domain wall energy for determining the pinning energy barrier in the creep law, and allows for prediction of the size of the effect of strain on creep velocity.
Domain wall energy depends on the balance of magnetic anisotropy energy and symmetric and antisymmetric exchange energies, which are all affected by the structural parameters of trilayer thin films, such as the magnetic layer thickness. In order to tune the domain wall velocity in perpendicular anisotropy thin films, materials should be designed not only by considering the commonly measured magnetic anisotropy energy, but also the symmetric and antisymmetric exchange energies. These factors should be balanced to produce a large change in domain wall energy for a given strain.
Acknowledgments
The authors acknowledge financial support from EPSRC, UK. (Grants No. EP/K003127/1 and No. EP/M000923/1).
Data availability
Data associated with this paper are available from https://doi.org/10.5518/410