Abstract
The results reported in (2010 Class. Quantum Grav. 27 025002) are special cases of a general treatment of canonical variables for dilaton gravity models published in (2009 Class. Quantum Grav. 26 035018).
Export citation and abstract BibTeX RIS
Different sets of canonical variables for 1 + 1-dimensional models of gravity without local physical degrees of freedom have been discussed in [1]. These variables are related to connection formulations as used in classical theories underlying loop quantum gravity. All models of this form are contained in the class of 2-dimensional dilaton models, or equivalently in the class of Poisson Sigma models [2–4]. Since these classes had already been formulated in terms of connection variables [5], there should be a strict relation between the different sets of variables. In this comment we work out the relationship.
We start with standard formulations of 1 + 1-dimensional actions for a dyad ea with volume form  , a connection 1-form ω and a dilaton field ϕ. For our purpose here, it suffices to consider torsion-free models, such that the condition
, a connection 1-form ω and a dilaton field ϕ. For our purpose here, it suffices to consider torsion-free models, such that the condition 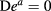 , using the covariant derivative given by ω, is implemented by Lagrange multipliers Xa. The dilaton gravity action with potential
, using the covariant derivative given by ω, is implemented by Lagrange multipliers Xa. The dilaton gravity action with potential  is then
is then
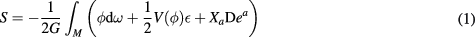
and takes, after integrating by parts, the form
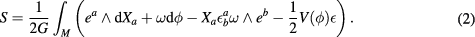
Here, M is a 1 + 1-dimensional manifold with coordinates (t, x).
In Poisson Sigma models, one organizes the variables in new sets 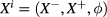 ,
, 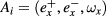 , and
, and 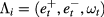 . A canonical analysis leads to Poisson brackets
. A canonical analysis leads to Poisson brackets

while the 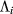 serve as Lagrange multipliers of first-class constraints
serve as Lagrange multipliers of first-class constraints


The variables introduced in [5] are obtained by using the 'absolute values'
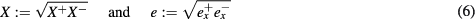
and boost parameters α and β in
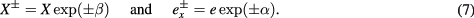
They are related to the canonical variables
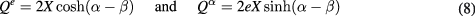
with
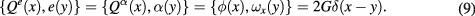
The inverse transformation is

In canonical variables, the constraints are

and

For spherically symmetric gravity, corresponding to a specific dilaton potential 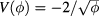 [4], one can compare the new canonical variables to those used in real connection formulations such as [6], denoted as
[4], one can compare the new canonical variables to those used in real connection formulations such as [6], denoted as  and with Poisson brackets
and with Poisson brackets
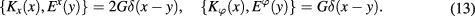
(Note that there is no factor of two in the second equation because the pair 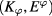 represents two angular directions which were independent before symmetry reduction.) They are related to
represents two angular directions which were independent before symmetry reduction.) They are related to 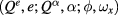 by the canonical transformation
by the canonical transformation
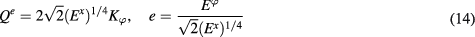

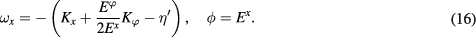
(Unlike the pair  , the pair (e,Qe) is defined with a factor of two in the Poisson bracket (9).) These relations have been derived in [5]; see equation (42) in this paper. Also in [5], the spherically symmetric Hamiltonian constraint has been obtained as
, the pair (e,Qe) is defined with a factor of two in the Poisson bracket (9).) These relations have been derived in [5]; see equation (42) in this paper. Also in [5], the spherically symmetric Hamiltonian constraint has been obtained as
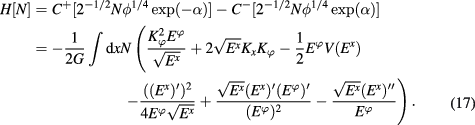
For an arbitrary dilaton potential, this formulation generalizes the connection formulation of spherically symmetric canonical gravity to arbitrary 1 + 1-dimensional dilaton models. Deriving just this kind of result was the aim of [1]. In fact, the definitions of [1] are nothing but the results of [5] with different names chosen for the new variables. The expression for e in (14) is the same as (51) in [1], Qe in (14) is (57), and 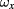 in (16) is (60).
in (16) is (60).
There is a different formulation in [1] for the specific case of the CGHS model (constant dilaton potential). This model, as presented in [1] has a Hamiltonian constraint with only 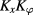 in its kinetic part but no contribution of
in its kinetic part but no contribution of 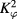 , unlike what we have in (17). However, this formulation is not new either, even though it does not correspond to a connection formulation as defined in [5]. It rather amounts to using the original canonical variables (8) of dilaton models, along with
, unlike what we have in (17). However, this formulation is not new either, even though it does not correspond to a connection formulation as defined in [5]. It rather amounts to using the original canonical variables (8) of dilaton models, along with 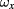 , and just renaming them as
, and just renaming them as 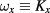 ,
, 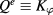 and
and 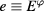 . Except for the new names, these variables, in particular Qe, have been introduced in [5]; see equation (20) in this paper. Except for using the SU(1,1)-invariant Qe, they correspond to a first-order formulation of Poisson Sigma models. The constraints (11) in these variables depend on
. Except for the new names, these variables, in particular Qe, have been introduced in [5]; see equation (20) in this paper. Except for using the SU(1,1)-invariant Qe, they correspond to a first-order formulation of Poisson Sigma models. The constraints (11) in these variables depend on  in a linear fashion, and so does the Hamiltonian constraint obtained by a linear combination. In these variables, therefore, the Hamiltonian constraint has only one term
in a linear fashion, and so does the Hamiltonian constraint obtained by a linear combination. In these variables, therefore, the Hamiltonian constraint has only one term 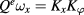 but not contribution from
but not contribution from  (which would amount to
(which would amount to 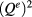 , but there is no such term in (11)). The quadratic term is introduced in (17) by applying the canonical transformation (14) and (16) via the product
, but there is no such term in (11)). The quadratic term is introduced in (17) by applying the canonical transformation (14) and (16) via the product  in (11).
in (11).
Even though [1] cites [5], it misses the close relationship between the results.
Acknowledgments
This work was supported in part by NSF grant PHY-1607414.


