Abstract
The evolution of particle coarsening due to a combined effect of Ostwald ripening and coagulation at the concluding stage of phase transition processes in metastable media is considered. A complete analytical solution of integro-differential equations with a memory kernel is found in special self-similar variables for supersaturated solutions and supercooled liquids. It is shown that the particle distribution function becomes narrower and bell-shaped when decreasing the metastability level. The analytical solutions obtained are in good agreement with experimental data.
Export citation and abstract BibTeX RIS
1. Introduction
In the absence of particle coagulation and integration, one can list three main stages of the phase transition process in metastable media. They are (i) an initial stage during which critical nuclei of the new phase appear and evolve when the system metastability level may be regarded as roughly constant, (ii) an intermediate stage during which crystal growth concurrently with continuing nucleation of particles and metastability reduction are equally important, and (iii) a final relaxation stage of Ostwald ripening in which larger particles grow at the expense of the dissolution of smaller ones.
The first stage was studied by a number of authors [1, 2]. The evolution of a metastable system at the second stage was analytically described in a complete form very recently for single-component and binary systems [3, 4]. The final stage of phase transformations was analyzed for cases when one of the particle coarsening mechanisms (Ostwald ripening or coagulation) predominates [5–8]. However, these mechanisms cannot always be identified separately [9, 10]. In addition, it is important to study their combined effect for the following reasons. The metastability level decreases at the concluding stage of phase transitions and tends to zero, whereas the radius of critical nuclei increases. As a result, fine crystals vanish, and large crystals continue to grow. It was previously assumed that this process predominates and it was described by means of the Lifshitz–Slyozov (LS) theory [11, 12] in which it was shown that (i) the cube of the average particle radius is a linear function of time t, and (ii) the cube of the supersaturation and the number of particles per unit volume represent inverse functions of time in the limiting case  . Although qualitative behavior of the LS asymptotic theory has been confirmed [13, 14], there are a lot of discrepancies between experimental data and theoretical and numerical predictions [15, 16]. It has been suggested that this situation can be connected with the effect of competition for space by the growing crystals [17]. This study showed that allowance for this competition greatly affects the size distribution function [18]. It is significant that both mechanisms, Ostwald ripening and coagulation, make a contribution of the same order of magnitude to the coarsening of particles [16, 19].
. Although qualitative behavior of the LS asymptotic theory has been confirmed [13, 14], there are a lot of discrepancies between experimental data and theoretical and numerical predictions [15, 16]. It has been suggested that this situation can be connected with the effect of competition for space by the growing crystals [17]. This study showed that allowance for this competition greatly affects the size distribution function [18]. It is significant that both mechanisms, Ostwald ripening and coagulation, make a contribution of the same order of magnitude to the coarsening of particles [16, 19].
From the physical point of view the present study is interesting as it combines two mechanisms of coalescence and coagulation simultaneously for a long-duration self-similar stage of the phase transition process. From the mathematical point of view the present analysis is of some interest because we discuss here how to solve analytically a modified kinetic equation involving nonlinear terms which are responsible for these mechanisms. In view of the fact that a general theoretical method to solving the problem containing the kinetic integral equation with a memory kernel is absent, the most popular approach is to apply different numerical methods [20–23]. Another widespread approach is concerned with situations in which one of the aforementioned mechanisms predominates. To solve such problems, some researchers have been proposing to look for different approximate solutions of the corresponding kinetic and balance equations (e.g. the conventional methods of Laplace transforms and expansion of solutions with respect to a small parameter) [24–26]. Therefore, the question remains open, of how to develop the appropriate theoretical method of solution of this combined nonlinear problem involving the mechanisms of coalescence and coagulation. In this paper, a new analytical approach taking into account both mechanisms simultaneously is developed, seemingly for the first time. An important point is that this approach can be used for the description of numerous phenomena in fundamental and applied research, ranging from applications relating to the condensation and crystallization of liquids, to chemical industry, geophysics and atmospheric sciences.
2. The model and its analytical solution
Consider a late stage of phase transformation (condensation or crystallization), when a metastable system is only slightly supersaturated/supercooled and nucleation has come to a halt because the critical nucleus size is large enough. In addition, the critical nucleus volume v* is also large and comparable with the average volume of the growing particles. Crystals with dimensions smaller than the critical volume v* vanish, whereas particles with larger dimensions evolve. An important point is that the moving particles collide and agglomerate so that the process becomes more complicated than in the case of Ostwald ripening. Namely, two small particles which should normally vanish (e.g. dissolve or evaporate) are capable of merging to grow into a larger particle able, perhaps, to evolve.
The polydisperse ensemble of particles is described by their size density distribution function f(t, v) normed to the particle denumerable concentration (v and t are the particle volume and time). Let us consider the mean-field approximation in which the notion of space is not present. The kinetic equation of Ostwald ripening corrected for coagulation can be written as [10, 11, 19, 27]
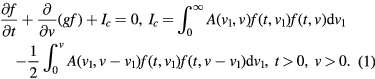
The first two terms in equation (1) represent the standard continuity equation and the integral Ic is the coagulation term obtained by Lifshitz and Slyozov [11]. The factor 1/2 in this term is needed to eliminate the collisions between two groups of crystals twice (for more details, see [11, 28]). Here g(t, v) is the growth rate of a particle with volume v and A(v1, v) is the frequency of paired collisions per unit volume. For the sake of simplicity, one can assume an equal coagulation rate for all the particles irrespective of their size, i.e. 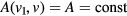 . In the case of supersaturated solutions, the growth rate can be written in the form [12]
. In the case of supersaturated solutions, the growth rate can be written in the form [12]
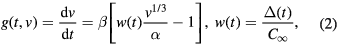
where 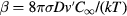 is the kinetic parameter,
is the kinetic parameter, 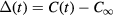 is the system supersaturation, and
is the system supersaturation, and 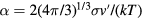 . Here C(t) and
. Here C(t) and  represent the gradually reducing volume concentration of the dissolved substance and its value at a planar interface, D and
represent the gradually reducing volume concentration of the dissolved substance and its value at a planar interface, D and 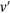 are the diffusion coefficient and the volume per atom of the dissolved component, σ is the surface tension, k is the Boltzmann constant, and T is the absolute temperature. In the case of supercooled melts the dimensionless supersaturation w should be replaced by the dimensionless supercooling [29]
are the diffusion coefficient and the volume per atom of the dissolved component, σ is the surface tension, k is the Boltzmann constant, and T is the absolute temperature. In the case of supercooled melts the dimensionless supersaturation w should be replaced by the dimensionless supercooling [29] 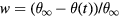 , where θ and
, where θ and 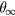 stand for the liquid temperature and its equilibrium value above the planar interface. As is easily seen from expression (2), the critical nucleus volume is
stand for the liquid temperature and its equilibrium value above the planar interface. As is easily seen from expression (2), the critical nucleus volume is 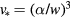 . This expression assumes that the critical nucleus is a sphere (because of the definition of α). In many cases, this approximation is not good (see, among others, [30]) and the theory under consideration should be modified in accordance with more precise expressions. However, in order to demonstrate the analytical method let us use here the aforementioned expressions.
. This expression assumes that the critical nucleus is a sphere (because of the definition of α). In many cases, this approximation is not good (see, among others, [30]) and the theory under consideration should be modified in accordance with more precise expressions. However, in order to demonstrate the analytical method let us use here the aforementioned expressions.
Note that the kinetic equation (1) should be supplemented by the following mass or heat balance equations
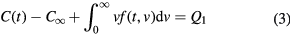
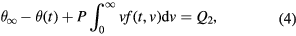
where P = L/Cm, L and Cm are the latent heat of the phase transition and the specific heat of the mixture, and Q1 and Q2 stand for the initial saturation and supercooling in the absence of crystals.
The integro-differential problem (1)–(4) is extremely complex. Note that even in the absence of coagulation (integral) terms in equation (1), the problem under consideration can only be solved asymptotically in the limit of large times [11, 31, 32]. We consider a final stage of the phase transition taking into account the integral contributions in equation (1). In this case, the system supersaturation 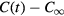 (or supercooling
(or supercooling 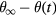 ) is much smaller than the initial supersaturation Q1 (or initial supercooling Q2), which makes it possible to neglect these terms in the balance equations (3) and (4). Also, note that the problem under consideration must be supplemented with the boundary condition at infinity of the form
) is much smaller than the initial supersaturation Q1 (or initial supercooling Q2), which makes it possible to neglect these terms in the balance equations (3) and (4). Also, note that the problem under consideration must be supplemented with the boundary condition at infinity of the form  .
.
Let us introduce the following self-similar variables
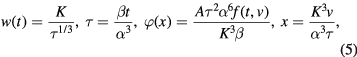
where parameter K characterizes the self-similar solution. Note that it cannot be determined by considering the concluding self-similar stage under consideration, and thus must be regarded as experimentally specified (this parameter characterizes the rate of metastability reduction). Now substituting expressions (5) into equations (1)–(4), one can get
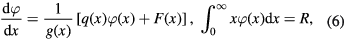
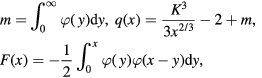
where 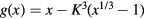 and
and  in the case of supersaturated solutions and
in the case of supersaturated solutions and 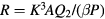 in the case of supercooled liquids.
in the case of supercooled liquids.
Note that at  equation (6) has no solution. This is due to the fact that the integral expression for R diverges at some point x where g(x) becomes zero. Note that the integro-differential equation (6) has been solved numerically [20, 33] at K < K0 on the basis of approximate estimates of the asymptotic behavior of
equation (6) has no solution. This is due to the fact that the integral expression for R diverges at some point x where g(x) becomes zero. Note that the integro-differential equation (6) has been solved numerically [20, 33] at K < K0 on the basis of approximate estimates of the asymptotic behavior of  at
at 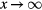 . The classical solution describing the ripening problem without coagulation exists merely at K = K0 [11, 12].
. The classical solution describing the ripening problem without coagulation exists merely at K = K0 [11, 12].
Numerical solutions of the integro-differential system (6) show that the dimensionless distribution function φ is of an order of magnitude less than 10−1 for all values of variable x. Estimating this function as  one can find from equation (6) that
one can find from equation (6) that  . Therefore the zero-order approximation
. Therefore the zero-order approximation 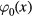 of the distribution function can be found from the following differential equation
of the distribution function can be found from the following differential equation 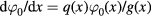 . Its integration gives
. Its integration gives
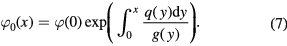
Substituting equation (7) into the integral for F, one can obtain its zero-order approximation
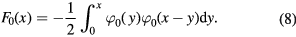
Now substitution of equation (8) into the right-hand side of the first equation (6) leads to

Integrating this equation one can find the first-order solution 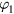 for the distribution function. Then the aforementioned expression for F determines its first-order approximation F1. By iterating this procedure over and over, we obtain the following complete solution
for the distribution function. Then the aforementioned expression for F determines its first-order approximation F1. By iterating this procedure over and over, we obtain the following complete solution
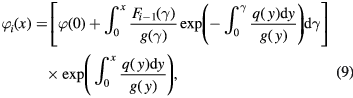
where
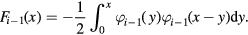
and i = 1, 2, 3,... Thus  from (7) represents the main contribution whereas
from (7) represents the main contribution whereas 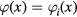 from (9) is the ith approximation of the complete solution for the distribution function
from (9) is the ith approximation of the complete solution for the distribution function 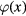 .
.
3. Results and conclusions
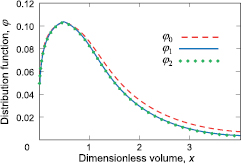
Figure 1 shows the complete analytical solution of the problem under consideration (here we chose K and 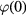 on the basis of estimations given by Alyab'eva and Mansurov [33]). As is seen, the zero-order solution
on the basis of estimations given by Alyab'eva and Mansurov [33]). As is seen, the zero-order solution 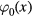 represents the main contribution to the distribution function. The first- and second-order solutions (
represents the main contribution to the distribution function. The first- and second-order solutions (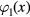 and
and  ) lie in close proximity to
) lie in close proximity to 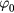 . In other words, the two next contributions
. In other words, the two next contributions 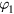 and
and 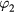 converge to the complete solution so that
converge to the complete solution so that 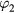 does not change significantly the resulting distribution function. Note that the infinite series (9) quickly converges due to smallness of the integral term F in comparison with the product
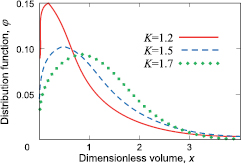
does not change significantly the resulting distribution function. Note that the infinite series (9) quickly converges due to smallness of the integral term F in comparison with the product 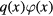 in the right-hand side of the first equation (6). Figure 2 demonstrates that the distribution function φ becomes broader and flatter and its maximum point moves to the right with increasing parameter K. This is due to the fact that parameter K is directly proportional to the metastability level w in accordance with the first equation (5). In other words, smallness of K implies smallness of w.
in the right-hand side of the first equation (6). Figure 2 demonstrates that the distribution function φ becomes broader and flatter and its maximum point moves to the right with increasing parameter K. This is due to the fact that parameter K is directly proportional to the metastability level w in accordance with the first equation (5). In other words, smallness of K implies smallness of w.
Figure 1. The distribution function φ plotted on the basis of analytical solutions (7) and (9) versus dimensionless volume x; K = 1.5, 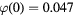 , m = 0.17.
, m = 0.17.
Download figure:
Standard image High-resolution imageFigure 2. The distribution function φ versus dimensionless volume x for different values of K.
Download figure:
Standard image High-resolution imageBy using self-similar variables (5) one can derive the following expressions for the mean particle radius 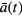 and the total number of particles N(t):
and the total number of particles N(t):

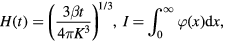
which demonstrate that 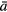 increases as t1/3 and N decreases in inverse proportion to time. This behavior corresponds to the classical case of Ostwald ripening without coagulation [7, 12].
increases as t1/3 and N decreases in inverse proportion to time. This behavior corresponds to the classical case of Ostwald ripening without coagulation [7, 12].
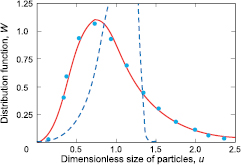
Figure 3 demonstrates the distribution function 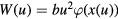 plotted according to the complete analytical solution (9) in comparison with experimental data [16] (here
plotted according to the complete analytical solution (9) in comparison with experimental data [16] (here 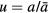 ,
,  ,
, ![$l=K\bar{a}{{\left[4\pi /\left(3\beta t\right)\right]}^{1/3}}$](https://content.cld.iop.org/journals/0953-8984/28/3/035102/revision1/cmaa0cb2ieqn043.gif) , and a represents the particle radius). Notwithstanding the fact that Ostwald ripening predominates in these experiments (in comparison with particle coagulation), these data were chosen because the theory under consideration and experimental data [16] describe the concluding stage of phase transitions where the self-similar regime establishes. In addition, experimental data [16] were chosen due to the fact that (i) experimental conditions and theoretical considerations are very similar, and (ii) experimental curves of the distribution function enable us to find all combinations of unknown theoretical parameters.
, and a represents the particle radius). Notwithstanding the fact that Ostwald ripening predominates in these experiments (in comparison with particle coagulation), these data were chosen because the theory under consideration and experimental data [16] describe the concluding stage of phase transitions where the self-similar regime establishes. In addition, experimental data [16] were chosen due to the fact that (i) experimental conditions and theoretical considerations are very similar, and (ii) experimental curves of the distribution function enable us to find all combinations of unknown theoretical parameters.
Figure 3. The distribution function W versus dimensionless particle size u in comparison with experimental data [16] of a tetradecane in water emulsion. The system parameters l = 0.5 and b = 14.1 are estimated on the basis of experimental curves. The dashed curve demonstrates the LS solution corresponding to coalescence without coagulation.
Download figure:
Standard image High-resolution imageAs is easy to see, the particle size distribution is in quantitative agreement with conducted experiments. The obtained distribution function taking into account the processes of coalescence and coagulation substantially differs from the LS asymptotic solution [11, 12] found in the absence of coagulation (solid and dashed lines in figure 3). Analytically this case is described by equation (1) in the absence of integral terms (Ic = 0). An important point is that the dashed curve in figure 1 (the LS solution) exists only at 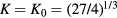 and equals zero for x > 27/8. The theory of coalescence combined with coagulation, contrastingly, has a solution at K < K0 on the right of the blocking point x = 27/8. In other words, the coagulation process substantially changes the Ostwald ripening stage of phase transitions. From the physical point of view this is explained by the competition of two evolutionary mechanisms (coalescence and coagulation) when coalescence plays an important role and particles approach each other due to Brownian motion (or another reason) and stick together. This situation completely differs from the Ostwald ripening mechanism when larger particles grow at the expense of smaller ones.
and equals zero for x > 27/8. The theory of coalescence combined with coagulation, contrastingly, has a solution at K < K0 on the right of the blocking point x = 27/8. In other words, the coagulation process substantially changes the Ostwald ripening stage of phase transitions. From the physical point of view this is explained by the competition of two evolutionary mechanisms (coalescence and coagulation) when coalescence plays an important role and particles approach each other due to Brownian motion (or another reason) and stick together. This situation completely differs from the Ostwald ripening mechanism when larger particles grow at the expense of smaller ones.
In summary, we have presented a theoretical investigation of particle coarsening kinetics with allowance for Ostwald ripening and coagulation at the concluding stage of phase transition processes. A complete analytical solution of the problem is found within the framework of the mean-field approximation when the particles interact only via a common mean-field, and their coagulation rate is constant. The obtained analytical solution of integro-differential equations demonstrates that the particle distribution function decreases and becomes broader and flatter when increasing the dimensionless volume x and highly depends on metastability reduction dynamics.
Acknowledgments
This work was supported by the Ministry of Education and Science of the Russian Federation under the project 315 and by the contract 02.A03.21.0006 (act 211 of Government of the Russian Federation).