Abstract
A mean field model is presented for the configuration dependent effective demagnetizing and anisotropy fields in assemblies of exchange decoupled magnetic particles of arbitrary shape which are expressed in terms of the demagnetizing factors of the particles and the volumetric shape containing the assembly. Perpendicularly magnetized two-dimensional (2D) assemblies have been considered, for which it is shown that the demagnetizing field is lower than the continuous thin film. As an example of these 2D systems, arrays of bistable cylindrical nanowires have been characterized by remanence curves as well as ferromagnetic resonance, serving to show the correspondence of these measurements with the model and also to validate the mean field approach. Linear chains of cylinders and spheres have been analyzed, leading to simple expressions to describe the easy axis rotation induced by the interaction field in chains of low aspect ratio cylindrical particles, and the dipolar magnetic anisotropy observed in the linear chain of spheres. These examples serve to underline the dependence on the dipolar interaction field and effective demagnetizing factor of the contributions that arise from the shape of the outer volume.
Export citation and abstract BibTeX RIS
Assemblies or arrays of exchange decoupled magnets represent a very large class of magnetic systems which are of great interest in different subjects and problems in magnetism at both fundamental and technological levels [1–4]. These include assemblies in which the particles are arranged or dispersed on a substrate or embedded in different media such as liquids, polymers or other nonmagnetic materials [5–7]. Depending on their spatial disposition, and thus the shape or outer volume that contains the assembly, they form one, two or three-dimensional (3D) heterostructures or composites [5, 6, 8–10].
The magnetic properties of a single isolated particle are mainly governed by the shape and magnetocrystalline anisotropy and eventually a magnetoelastic contribution. In an assembly of many of such particles, their individual properties are further modified by the interaction field produced by the other particles. If the particles are not allowed to come into contact, then the interaction is purely dipolar and has the same magnetostatic origin as the demagnetizing field and shape anisotropy associated with each particle. In this sense, from a mean field perspective, an effective demagnetizing field which includes the particle self-demagnetizing field as well as the dipolar interaction is a common feature of any assembly of exchange decoupled particles [11, 12]. Consequently, these considerations should apply to any assembly of particles, whether the particles are magnetically hard or soft, and regardless of the approach or level of approximation used to describe them. In particular, it should be possible to interpret the vast phenomenology of effects associated with the dipolar interaction or the effective demagnetizing field within this framework [13–19]. However, this is usually complicated by the difficulty of finding either adequate expressions or reliable measurements for the dipolar interaction. Furthermore, extensions to include the magnetization or configuration dependency of the dipolar interaction field adds additional difficulties for establishing a suitable description for these systems.
A coherent formulation is required for the effective demagnetizing field which allows us to include the configuration dependent interaction field for an assembly of particles of arbitrary shape and outer volume and that allows us to determine how the interaction field will modify the demagnetizing field, the effective anisotropy or total energy and coercivity of the system.
The present study is focused on deriving mean field expressions for the configuration dependent effective demagnetizing and anisotropy fields in assemblies of exchange decoupled magnetic particles, which depend on the shape of the particles, the volume containing them and the packing fraction. The magnetostatic properties of two- and one-dimensional (2D and 1D) assemblies have been analyzed and the results show that the dipolar interaction depends not only on the interparticle distance but also on the outer shape of the assembly. In particular it is shown that this outer shape contribution to the dipolar field plays an important role in the coercivity of the assembly, the limiting values of the effective demagnetizing fields and the magnetization reorientation transition due to the dipolar interaction. Remanence curves and ferromagnetic resonance measurements done on arrays of bistable cylindrical nanowires have served first to identify the correspondence of these measurements with the model and, second, to validate this mean field approach.
The present study is structured as follows. In section 1 the experimental details and techniques are presented. Section 2, considers the formalism for the effective demagnetizing field, first for the particular case where the assembly is saturated and then the expressions are derived for the non-saturated case, which introduces the dependence on the magnetic configuration of the assembly. In section 3 the formalism is applied first to the case of perpendicularly magnetized 2D arrays, then to the particular case of arrays of nanowires where the expressions are compared with the experimental data, and finally these expressions are applied to linear chains of cylinders and spheres. In section 4 a detailed discussion of the results is presented.
1. Experimental details
Arrays of Co, Ni81Fe19 and Co55Fe45 nanowires having a low density (low porosity P) and small diameter (29 ≥ ϕ ≥ 40 nm) have been grown by electrodeposition into the pores of 21 μm thick lab-made track-etched polycarbonate (PC) membranes, in which the pores are parallel to each other but randomly distributed [20]. Also, two samples have been fabricated using anodized alumina templates in order to have higher porosities (10 and 15%). Full details of the preparation process can be found elsewhere [21].
For the electrodeposition a Cr/Au layer is evaporated previously on one side of the membrane to serve as a cathode and deposition is done at a constant potential using a Ag/AgCl reference electrode. For CoFe a 40 g l−1 FeSO4 + 80 g l−1 CoSO4 + 30 g l−1 H3BO3 electrolyte was used with a potential of V =− 0.9 V, while for NiFe the electrolyte contained 5.6 g l−1 FeSO4 + 131.4 g l−1 NiSO4 + 30 g l−1 H3BO3 and deposition is done at V =− 1.1 V. Cobalt nanowires have been grown at V =− 1 V using a 238.5 g l−1 CoSO4 + 30 g l−1 H3BO3 electrolyte with the pH set to 2.0 by addition of H2SO4 to favor a polycrystalline fcc-like Co structure with no magnetocrystalline anisotropy contribution [22]. Table 1 shows the details of the samples considered.
Table 1.
Co, NiFe and CoFe nanowire samples used in this study are numbered as s1–s16. For each sample the following quantities are given: the wire diameter Φ, nominal packing fraction PN, the FMR effective field Heff, the dipolar interaction coefficient αz, and the determined values of the packing fraction Pm and saturation magnetization  .
.
| Material | Sample | Φ (nm) | PN (%) | Heff (kOe) | αz (Oe) | Pm (%) |

|
|---|---|---|---|---|---|---|---|
| Co | s1 | 39 | 4.8 | 7.65 | 400 | 4.63 | 1415 |
| Co | s2 | 40 | 5.6 | 7.48 | 440 | 5.09 | 1406 |
| Co | s3 | 30 | 3.9 | 7.57 | 240 | 2.91 | 1319 |
| Co | s4 | 40 | 2.5 | 8.13 | 140 | 1.63 | 1360 |
| Co | s5 | 30 | 3.9 | 7.77 | 362 | 4.08 | 1409 |
| Co | s6 | 40 | 1.7 | 8.45 | 118 | 1.23 | 1396 |
| Co | s7 | 30 | 4.2 | 7.68 | 370 | 2.85 | 1337 |
| Co | s8 | 29 | 3.65 | 7.69 | 350 | 2.98 | 1343 |
| NiFe | s9 | 30 | 3.46 | 4.64 | 140 | 3.19 | 816 |
| NiFe | s10 | 40 | 3.4 | 4.45 | 180 | 3.58 | 792 |
| NiFe | s11 | 35 | 8.8 | 5.62 | 580 | 7.87 | 1171 |
| NiFe | s12 | 35 | 12 | 3.34 | 635 | 11.52 | 812 |
| CoFe | s13 | 40 | 3.9 | 10.52 | 400 | 3.42 | 1868 |
| CoFe | s14 | 29 | 5 | 10.24 | 640 | 5.23 | 1933 |
| CoFe | s15 | 29 | 5 | 9.18 | 520 | 4.77 | 1706 |
| CoFe | s16 | 18 | 10 | 8.45 | 1274 | 10.4 | 1953 |
Ferromagnetic resonance (FMR) measurements were done in the field swept mode with frequencies ranging from 1 up to 50 GHz using a 150 μm wide microstripline with the DC magnetic field applied parallel to the long axis of the wires, as detailed elsewhere [21, 22, 18]. For all the samples considered, the transmission spectra are recorded at a fixed frequency while the magnetic field is swept from 10 down to 0 kOe. These measurements are repeated for different frequencies and the dispersion relation is obtained from the collection of frequencies and their respective resonance field. Figure 1(a) shows typical dispersion relations obtained on the samples. The dispersion relation for an array of infinitely long cylindrical nanowires with the field applied parallel to the wires which are in the saturated state is [18]

where HRes and Heff are the resonance and effective anisotropy field, respectively. From the linear fit of the dispersion relation (see figure 1(a)) the values of Heff have been determined for each sample, and the corresponding values are given in table 1.
Figure 1. (a) Typical dispersion relations obtained on arrays of NWs with the field applied parallel to the wires; the measurements are shown as symbols, while the continuous line is the best fit using equation (1). (b) Isothermal remanence magnetization (IRM, blue) and DC demagnetization (DCD, red) remanence curves measured on sample s10 [NiFe] with the field applied parallel to the nanowire axis.
Download figure:
Standard image High-resolution imageIsothermal remanence magnetization (IRM) and DC demagnetization (DCD) remanence curves measurements with the field applied parallel to the wires axis, have also been done in all the samples, from which the interaction field coefficient along the wire axis, αz, has been determined as [23]

where  is the field value at which the normalized IRM curve is 0.5, while
is the field value at which the normalized IRM curve is 0.5, while  is the field value at which the DCD curve is zero, as shown in figure 1(b). The values determined for the interaction field coefficient αz are given in table 1.
is the field value at which the DCD curve is zero, as shown in figure 1(b). The values determined for the interaction field coefficient αz are given in table 1.
2. The effective demagnetizing field
Consider an assembly of exchange decoupled identical particles where each one has a demagnetizing factor given by N, called the inner demagnetizing factor, contained within a macroscopic volume described by an outer demagnetizing factor N+, as schematically shown in figure 2. Furthermore, all the particles are aligned so their easy axes point in the same direction. The energy density of a given particle can include the magnetocrystalline (KMC), shape (KS) and magnetoelastic (KME) anisotropies, which determine the total anisotropy of the particle, KA = KMC + KS + KME, as well as a contribution due to the interparticle interaction (Eint)

where the shape anisotropy and the dipolar interaction are of magnetostatic origin and are related to the effective demagnetizing fields, which are considered in the following sections. Furthermore, in the following it will be assumed that the particles are homogeneously magnetized regardless of their shape.
Figure 2. Schematics of an assembly of identical particles characterized by an inner demagnetizing factor N contained within a macroscopic volume geometrically characterized by the outer demagnetizing factor N+ (dashed lines).
Download figure:
Standard image High-resolution image2.1. Saturated state
The effective or total demagnetizing factor can be expressed using the interpolation procedure introduced by Netzelmann [24]. To simplify the notation, in the following the effective or total demagnetizing factor (Neff) will be denoted as NT which can be expressed in terms of the packing fraction P as [24, 25]

However, for the treatment of an assembly of magnetic particles it is more useful to rewrite this last expression as

The first term on the right-hand side corresponds to the self-demagnetizing factor of the particles that makeup the assembly, i.e. Nself, while the second term contains all the contributions that depend on the packing and corresponds to the dipolar interaction contribution Ndip, then

When P = 0 the demagnetizing factor reduces to that of an isolated non-interacting particle. The opposite limit, P → 1, leads to the outer demagnetizing factor. If both the inner and outer demagnetizing factors are diagonal and their trace is Tr(N) = 4π, then from equation (5)
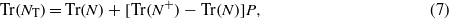
and from the form of (6) the following properties of NT are obtained:


The ith component of the effective demagnetizing field in the saturated state for an assembly of particles follows from equation (5)
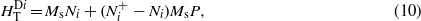
where the first term is the usual self-demagnetizing field of the particle,  , and the second term is the dipolar interaction field, this is
, and the second term is the dipolar interaction field, this is

The total or effective magnetostatic anisotropy field in the saturated state is defined as  , where the hard axis is along the x-direction and the easy axis is taken along the z-axis, then
, where the hard axis is along the x-direction and the easy axis is taken along the z-axis, then
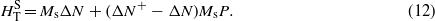
The first term on the right-hand side is the shape anisotropy field of the individual particles (HS), while the second term corresponds to the total or effective dipolar field in the saturated state:

The total shape (magnetostatic) anisotropy energy is given by  , which includes both the shape anisotropy of the particle and the contribution of the dipolar interaction. This anisotropy constant now regroups KS and Eint in equation (3).
, which includes both the shape anisotropy of the particle and the contribution of the dipolar interaction. This anisotropy constant now regroups KS and Eint in equation (3).
Finally, from the expressions obtained for the interaction field there are two other relations of interest that follow when both the inner and outer volumes have in-plane symmetry, so that Nx = Ny. Due to the symmetry, the in-plane components of the interaction field are equal,  , and since Tr(Ndip) = 0, according to equation (9), the following relation between the components of the dipolar fields is obtained:
, and since Tr(Ndip) = 0, according to equation (9), the following relation between the components of the dipolar fields is obtained:

This shows that when both the inner and outer volume have rotational symmetry, the dipolar interaction field along the symmetry axis is twice the dipolar field in the hard axis with opposite sign. This, for example, has been obtained by several authors [26, 27]. A consequence of this result is that the dipolar part of the total or effective anisotropy field ( ) is
) is

which provides a relation between the component of the interaction field along the easy axis, with the net contribution of the interaction field to the total anisotropy field.
2.2. Non-saturated states
To extend the previous expressions to the non-saturated case, consider that the particles are bistable, this is, they can only be magnetized along their easy axis in both the positive or negative direction. The normalized magnetization, m = M(H)/Ms, so that −1 ≤ m ≤ 1. Any magnetic state, called hereafter m, can be written in terms of the fraction of particles magnetized in the positive (m+) and negative (m−) directions, with 0 ≤ m± ≤ 1, and m = m+ − m−. Moreover, since the number of particles is constant, m+ + m− = 1, and m± can be obtained from the value of m as

A recent FMR study done on non-saturated arrays of bistable nanowires led to the expressions for the effective field, the dipolar interaction term and the FMR dispersion relation that include explicitly the magnetic configuration of the system [28, 29]. In particular, it was shown that to extend the known expressions for the saturated case to the non-saturated case, it is necessary to rewrite the dipolar interaction term as a parametric expression of m± [28, 29]. Assuming a dipolar interaction field of the form αm, it implies that the dependence of the interaction field on m is not as a direct product but instead requires using equation (16); this is

which at saturation reduces to the expected value. The ± sign is introduced to include both positive (m = 1) and negative (m =− 1) saturation.
Using equation (10), the ith component of the effective demagnetizing field is
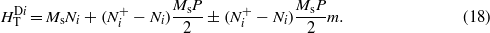
The dipolar contribution now contains two terms, the first one is constant while the second one is proportional to m and corresponds to the magnetization dependent part of the demagnetizing field. If the magnetization dependent interaction field is taken as αm, then from the last term on the right-hand side, the ith component of the dipolar interaction field coefficient α can be identified as
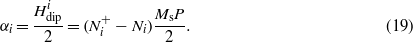
Then equation (18), can be written as

where  is the demagnetizing field of the isolated particle. From equation (12), the effective or total magnetostatic anisotropy field is
is the demagnetizing field of the isolated particle. From equation (12), the effective or total magnetostatic anisotropy field is

and αT = αx − αz is the total dipolar field coefficient. At saturation m = 1, both equations (20) and (21) reduce to equations (10) and (12), respectively.
As seen from these expressions, the effective demagnetizing field accounts for both the shape anisotropy of a particle in the assembly and the dipolar interaction it experiences. However, the existence of other anisotropy contributions, such as magnetocrystalline or magnetoelastic ones, will simply result in an additive term to the particle shape anisotropy. Indeed, the shape anisotropy as well as other anisotropy contributions will result in the effective anisotropy of the particle and will define the effective energy barrier of each of the particles in the assembly, and corresponds to the coefficient KA in equation (3) while the interaction field is accounted for by another term in the energy.
3. Applications
3.1. Two-dimensional arrays with rotational symmetry
An important class of magnetic assemblies are 2D arrays of exchange decoupled nanoparticles, ideally a monolayer of single domain particles, with perpendicular magnetization. These correspond, for example, to systems obtained by lithography, including perpendicular bit patterned media, also granular thin films with columnar structure like those used for perpendicular recording media, self-assembled monolayers and nanowire arrays [8, 9].
For these systems one can assume that the height of the particles is very small compared with the lateral dimensions of the entire array and the volume containing the particles can be considered as an infinite thin film, so that  and
and  , as depicted in figures 2(a) and (b). Using these values in equation (10) and assuming particles with in-plane symmetry so that Nx = Ny and using Nz = 4π − 2Nx to express quantities in terms of Nx, the effective demagnetizing field perpendicular to the plane (z) is
, as depicted in figures 2(a) and (b). Using these values in equation (10) and assuming particles with in-plane symmetry so that Nx = Ny and using Nz = 4π − 2Nx to express quantities in terms of Nx, the effective demagnetizing field perpendicular to the plane (z) is
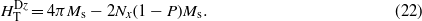
This shows that the effective demagnetizing field of a thin film made of exchange decoupled entities is less than 4πMs by a quantity equal to 2Nx(1 − P)Ms.
The total shape anisotropy field (equation (21)) is
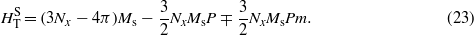
The first term on the right-hand side is the shape anisotropy of the particle, while the second and third terms correspond to the dipolar part of the total anisotropy field, for m = 1,

which is a particular case of equation (15). As seen from this expression Hdip is only a function of Nx and P. Since the particles have in-plane symmetry, then Nz = 4π − 2Nx, from where it follows that if 0 ≤ Nz ≤ 4π, then 0 ≤ Nx ≤ 2π. And from the previous expression for Hdip, it is possible to establish an upper bound for the dipolar part of the total or effective anisotropy. Taking Nx = 2π,

The dipolar contribution to the total anisotropy field is antiferromagnetic, inferred by the negative sign in equation (24), as expected for a 2D array of nanomagnets with perpendicular anisotropy.
Regarding the influence of the geometrical arrangement of the particles in a 2D assembly, this can be taken into account by using a proper definition for the packing fraction, since as seen in equations (23) and (24) the dipolar interaction is proportional to P. For example, the packing fraction for 2D hexagonal and square arrays are  and P = (πϕ2)/(4d2), respectively. Since these packings are not equal the dipolar interaction does depend on the arrangement of the particles.
and P = (πϕ2)/(4d2), respectively. Since these packings are not equal the dipolar interaction does depend on the arrangement of the particles.
3.2. Cylindrical nanowires
In the particular case of a 2D array of circular cylinders of arbitrary height aligned parallel to each other so their axes are along the z axis, as shown in figure 2(b), their effective demagnetizing fields along the easy and hard directions are given by equation (10). As in the previous section, the outer demagnetizing factor is taken as an infinite thin film. For a cylinder of arbitrary aspect ratio (wire height divided by its diameter), Nz can be determined numerically [30]. However, for the nanowires considered in this study, the wire height is typically of the order of 20 μm so the aspect ratio is very high, and they can be considered as infinite so their demagnetizing factors are Nz = 0 and Nx = Ny = 2π and from equation (10) the demagnetizing field along the easy and hard axes are


Due to the symmetry properties of both inner and outer demagnetizing factors,  and the dipolar terms satisfy both equations (9) and (14). The effective anisotropy field is
and the dipolar terms satisfy both equations (9) and (14). The effective anisotropy field is

which corresponds to the known expression for the effective field for an array of infinite cylindrical nanowires in the saturated state [18]. The effective dipolar interaction field is Hdip =− 6πMsP, and using equations (19) and (21), the magnetization dependent part of the effective interaction field is

in agreement with the expression obtained in [29].
On the other hand, the measurement of the interaction field using equation (2) and the IRM and DCD remanence curves is done solely along the wire axis, this is, the measurement is related to the component of the interaction field along this direction, as pointed out in [23]. From equation (26), and equations (19) and (20), the component of the magnetization dependent part of the interaction field along the wire axis is

Then equations (28), (29) and (30) provide different expressions for the interaction field which have different physical meanings. Moreover, depending on the measuring technique, each of these three quantities can be measured independently [18, 29, 23], so it is important to distinguish between them.
Since the effective anisotropy field  can be determined from the dispersion relation obtained from the FMR measurements, using equation (1), then from equation (28),
can be determined from the dispersion relation obtained from the FMR measurements, using equation (1), then from equation (28),  . So Hdip has been determined for each sample from the FMR measurements using the nominal values of Ms for Co (1400 emu cm−3), Ni81Fe19 (800 emu cm−3), and Co55Fe45 (1900 emu cm−3) and the values of Heff given in table 1. These values where then divided by 3 so they correspond numerically to equation (30) which is the value of the component of the interaction field along the wire axis measured with the IRM and DCD remanence curves. Figure 3 shows the values obtained using the IRM and DCD remanence curves, αz, plotted as a function of the values obtained by FMR, Hdip/3.
. So Hdip has been determined for each sample from the FMR measurements using the nominal values of Ms for Co (1400 emu cm−3), Ni81Fe19 (800 emu cm−3), and Co55Fe45 (1900 emu cm−3) and the values of Heff given in table 1. These values where then divided by 3 so they correspond numerically to equation (30) which is the value of the component of the interaction field along the wire axis measured with the IRM and DCD remanence curves. Figure 3 shows the values obtained using the IRM and DCD remanence curves, αz, plotted as a function of the values obtained by FMR, Hdip/3.
Figure 3. The easy axis component of the interaction field determined by magnetometry, αz = 2πMsP, plotted as a function of Hdip/3, where Hdip = 6πMsP is the total interaction field measured by FMR in the saturated state, for all the nanowire samples listed in table 1.
Download figure:
Standard image High-resolution imageThese results show a very good agreement, which shows that equations (28) and (30) both provide correct results for the interaction field. Moreover, these two expressions provide expressions for quantities that can be measured independently, so it is possible to find a self-consistent method to determine both Ms and P. Since  and αz are determined from FMR and magnetometry measurements, respectively, then combining equations (28) and (30) leads to the following expressions for Ms and P:
and αz are determined from FMR and magnetometry measurements, respectively, then combining equations (28) and (30) leads to the following expressions for Ms and P:


The values of  and αz measured by FMR and the remanence curves, respectively, that are given in table 1 have been used as input in equations (31) and (32) to obtain the corresponding values of Ms and P. The results are given in table 1 in the columns labeled Pm and
and αz measured by FMR and the remanence curves, respectively, that are given in table 1 have been used as input in equations (31) and (32) to obtain the corresponding values of Ms and P. The results are given in table 1 in the columns labeled Pm and  , respectively. As a first point, the values of
, respectively. As a first point, the values of  show a very good agreement with the known values for Co, NiFe and CoFe. Furthermore the values for NiFe and CoFe alloys are in good agreement with those determined solely by FMR and reported elsewhere [29, 31]. Regarding the values of the template porosity, comparing the nominal values determined by scanning electron microscopy PN with those determined by the measurements Pm, a very good agreement is also found in practically all the samples. This procedure is general and can be extended to other assemblies by solving for Ms and P using equations (12) and (19).
show a very good agreement with the known values for Co, NiFe and CoFe. Furthermore the values for NiFe and CoFe alloys are in good agreement with those determined solely by FMR and reported elsewhere [29, 31]. Regarding the values of the template porosity, comparing the nominal values determined by scanning electron microscopy PN with those determined by the measurements Pm, a very good agreement is also found in practically all the samples. This procedure is general and can be extended to other assemblies by solving for Ms and P using equations (12) and (19).
3.3. Linear chain
So far, only 2D systems with perpendicular magnetization have been considered. Another interesting example is that of the linear chain of particles, and particularly for circular cylinders of different aspect ratio and spheres, like those shown in figures 2(c) and (d), respectively. For an infinite number of particles, the outer demagnetizing factor is an infinite cylinder of circular cross section whose axis is assumed along the z axis so  and
and  . While for both spheres and cylinders, the components of the inner demagnetizing factor are Nx = Ny and Nz = 4π − 2Nx. From equation (12), the effective anisotropy field is
. While for both spheres and cylinders, the components of the inner demagnetizing factor are Nx = Ny and Nz = 4π − 2Nx. From equation (12), the effective anisotropy field is
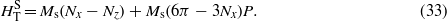
For the calculations, the demagnetizing factors and the packing fraction are required. For the chain of spheres, Nx = Ny = Nz = 4π/3 and the packing fraction is P = (2/3)ϕ/d, where d is the center to center distance and ϕ is the diameter of the sphere. For the cylinders, Nz is determined using known expressions as a function of the aspect ratio τ = h/ϕ, where h is the height of the cylinder [30], and in this case P = h/d. Figure 4(a) shows the reduced effective anisotropy  for linear chains of cylinders with different aspect ratio (τ = 0.5,0.8,2.5 and 5) as well as for a chain of spheres (dashed line).
for linear chains of cylinders with different aspect ratio (τ = 0.5,0.8,2.5 and 5) as well as for a chain of spheres (dashed line).
Figure 4. (a) Reduced effective anisotropy as a function of the reduced center to center distance d/ϕ for linear chains of cylinders with aspect ratio τ = 0.5,0.8,2.5 and 5 as well as for spheres (dashed line). (b) Zero anisotropy curve for a linear chain of cylindrical particles of aspect ratio τ as a function of the reduced center to center distance.
Download figure:
Standard image High-resolution imageConsider first the case of the linear chain of cylinders. For a single, isolated and non-interacting circular cylinder, the critical aspect ratio is τ = 0.9065; above this value, Nx > Nz and the easy axis is along the cylinder axis and at lower values Nx < Nz it is perpendicular to the axis. As seen in figure 4(a) at large distances the anisotropy tends asymptotically to the expected value of the isolated non-interacting cylinder, which yields negative values for τ = 0.5 and 0.8, and positive for τ = 2.5 and 5.
As the particles are brought closer the interaction increases. For τ > 0.9065, the interaction is ferromagnetic as it favors head to tail alignment of the magnetization, which results in an increase of the effective anisotropy as the packing fraction increases. For low aspect ratios (τ < 0.9065) the easy axis of a given cylinder is perpendicular to the chain axis and the first term in equation (33) is negative, so the interaction becomes antiferromagnetic as it has the opposite sign, and competes against it. As the packing fraction is increased, the value of the interaction increases and overcomes the anisotropy of the particle leading to a reorientation of the magnetization easy axis.
In other words, to have a reorientation of the magnetization easy axis due to the dipolar interaction, the interaction has to be of the demagnetizing type (antiferromagnetic) with respect to the easy axis direction of the particle when considered isolated. For the linear chain of cylinders there is a critical aspect ratio for the easy axis reversal which depends on the interparticle distance that corresponds to those values for which the effective anisotropy vanishes. Setting  in equation (33) and using 2Nx = 4π − Nz, the critical packing fraction can be expressed as
in equation (33) and using 2Nx = 4π − Nz, the critical packing fraction can be expressed as

which is only valid for Nz > 4π/3. Here Nz = Nz(τ) gives the dependence on the aspect ratio of the cylinder which is given by well known expressions [30]. Figure 4(b) shows the variation of the critical aspect ratio with the reduced center to center distance for a linear chain of cylinders. Above this curve, the magnetization lies along the cylinder axis and the interaction between them is ferromagnetic. Below this line, the magnetization easy axis is perpendicular to the cylinder axis and the dipolar interaction is antiferromagnetic. At large distances, this curve tends asymptotically to τ = 0.9065 (horizontal dashed line) which is the critical aspect ratio for an isolated non-interacting cylinder with Nz = 4π/3 [30]. The highest packing fraction required to reverse the easy axis is obtained when the axial demagnetizing factor of the disk, Nz, tends to 4π, which, from equation (34), corresponds to Pc = 2/3.
Finally, the linear chain of spheres presents features that are interesting, as seen in figure 4(a), in particular the existence of an effective anisotropy and its increase as the packing fraction increases, which in light of equation (33) is entirely due to the dipolar interaction. Indeed, as seen in the figure, the effective anisotropy tends to zero as the distance between particles is increased, consistent with a single sphere with no shape anisotropy. Moreover, the maximum value of the anisotropy is attained when the spheres come in contact and this value is lower than 2π, which shows that there is not a full equivalence between a cylindrical wire and the chain of spheres. This point has been brought to light recently and is important since modeling of cylindrical wires is commonly done by considering them as a chain of spheres [32, 33]. From equation (33), the maximum value of the effective anisotropy for the chain of spheres is reached at P = 2/3 and

as indicated in figure 4(a).
4. Discussion
Expressions for the magnetization dependent demagnetizing field and the magnetostatic anisotropy field (energy) have been derived. These are general as the inner and outer volume are arbitrary and apply to assemblies of identical exchange decoupled, bistable particles with a common easy axis. Moreover, this approach is a mean field approximation which only accounts for magnetostatic effects. In consequence, all the particles are equivalent which is only valid if the assembly contains a very large number of particles.
This also implies that the particles should have their easy axis aligned and parallel with all the other particles. If this is not the case, the expressions derived for the effective demagnetizing field cannot be applied as they are, since an averaging would be necessary. However, although this has been done for randomly oriented non-interacting particles [12], the presence of the interaction field complicates the problem because, among other things, different interactions (ferro- and antiferromagnetic) can be present at the same time and the model cannot account for this scenario.
Regarding the form of the effective demagnetizing field in the saturated state, equation (10), it contains the self-demagnetizing field of the individual particle and the component of the dipolar interaction field, equation (11), which is consistent with previous expressions obtained for nearly spherical particles [34]. On the other hand, when compared to other expressions [35], which provide non-physical results for particular limiting cases [11], equation (10) provides correct limiting values when P = 0 or 1. Moreover, based on more physical arguments and following Kronmüller's analysis [36], Dobrynin et al [37] derived an expression for the effective demagnetizing field which contains a term that depends on the difference of the outer and inner demagnetizing factors as in equation (11), which provides support for Netzelmann's interpolation [24].
The expression obtained for the effective demagnetizing field in the saturated state, equation (10), shows that this differs from that of the homogeneous material defined by the outer volume when P < 1. For the particular case of a perpendicularly magnetized assembly with an outer volume of a thin film, as shown by equation (22), the effective demagnetizing factor is lower than the continuous film,  , provided that P < 1 [38, 39].
, provided that P < 1 [38, 39].
The extensions to include the configuration dependence are done by taking the product between the interaction term for the saturated case and equation (16) on the component of the demagnetizing field along the easy axis, equation (18), and on the total anisotropy field, equation (21).
An important result is that the interaction field can be expressed in different forms each with different physical meaning, which, however, are interrelated. The dipolar interaction contributes to the components of the demagnetizing field, equation (10), as well as to the total magnetostatic anisotropy field, equation (12). Then each of these contributions can be extended to non-saturated states assuming an interaction field of the form αm, where the coefficient α is given by equation (19). The FMR and magnetometry measurements done on arrays of nanowires provide a validation of this approach, while showing that different measuring techniques can provide values that correspond to different forms of expression of the interaction field.
From the extension done to include the configuration dependency on the interaction field, the hysteresis loop shearing can be attributed to the magnetization dependent component of the effective demagnetizing field along the easy axis. As discussed in [23], assuming an interaction field of the form αm, the shearing can be corrected once the value of the coefficient is known, which; as shown here, is given by equation (19).
The coercive field in an assembly is defined with respect to the total or effective anisotropy of the entire system, regardless of the specific internal composition, and in the Stoner–Wohlfarth model these quantities are equal. If we call Hc(0) = MsΔN the coercive field of the isolated particle (P = 0), rearranging equation (12), the coercive field of the assembly is given by
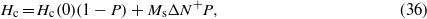
which depends on the packing fraction as well as on the outer volume. The first term is the well known dependence of the coercive field on the packing fraction in assemblies where the shape anisotropy prevails [40, 41]. The second term represents the anisotropy contribution of the outer volume, which implies that the coercivity of the assembly is shape dependent. So for a given assembly with fixed packing fraction, the coercive field will change between samples with different outer volume, as recently reported for granular hard magnetic films [42]. Moreover, for the particular case when the outer volume is isotropic and ΔN+ = 0, the second term vanishes. To further emphasize the importance of the second term in equation (36), notice that if only the first term is considered, the coercivity always decreases when the packing fraction increases, regardless of how the particles are distributed [40, 41]. This behavior is only consistent with the case where the interaction between the particles is antiferromagnetic. Indeed, for example, consider the linear chain of cylinders discussed above, each with their easy axis parallel to the chain axis, the interaction is ferromagnetic, and as the packing fraction increases, the coercivity of the entire chain should increase from the value of the isolated cylinder of finite aspect ratio to that of the infinite cylinder. This behavior is described by equation (36) when the second term is taken into account.
Since the total anisotropy field, equation (12), depends explicitly on this outer shape anisotropy MsΔN+P, then variations on the shape of the outer volume result in changes in the demagnetizing field, the anisotropy and, as just mentioned, in the coercivity. This contribution is associated only with the dipolar interaction, so at low packing it is weak, while at higher packing fractions it can induce appreciable effects, and can be used as an additional parameter to control the magnetic properties of the assembly. An interesting case is when the assembly is made by spherical particles, since their shape anisotropy vanishes and the effective anisotropy field is given only by the outer shape anisotropy. Then a chain of spheres will behave close to a cylinder (its outer volume) and the entire chain has a uniaxial anisotropy whose origin is the interparticle interaction field [32], while the same particles forming a spherical assembly will be isotropic. Although this is a well known result, it shows that this effect follows from the key role played by the outer demagnetizing factor on the value of the interaction field, which recently has been related to novel effects in granular hard magnets [42], composites [43] and dipolar ferromagnetic order in superparamagnetic particle monolayers [44].
Another effect related to this contribution is the magnetization reorientation transition induced by the interaction field, which was discussed for the linear chain of cylinders, but which has also been reported for other assemblies [17–19, 45, 46]. As discussed above, this transition results from increasing the packing fraction when the shape anisotropy of the single particle and the dipolar term have opposite signs. Qualitatively, this can also be interpreted as a competition between the shape anisotropies of the inner and outer volume and how their respective easy axes are oriented with respect to each other. At very low packing, the easy axis of a given particle in the assembly is that of the inner volume, while as P → 1 the easy axis corresponds to that of the outer volume. If both inner and outer volume have their easy axes in the same direction, there will be no reorientation transition of the magnetization, but if their easy axes are not aligned, this transition will take place above a certain critical packing fraction. In this sense, both inner and outer volumes should be anisotropic, since if either one of them is isotropic, there will be no transition. Moreover, an anisotropic outer volume is a necessary condition to induce this transition, as deduced from equation (36). Noting that in this expression Hc is the total shape anisotropy and Hc(0) = MsΔN corresponds to the inner volume shape anisotropy, it follows that the total anisotropy will never change sign if the second term is not included.
The validity of this mean field approach is determined mainly by the extent to which the individual particles in the assembly remain bistable and are able to rotate independently from other particles, this is, that no collective effects occur while individual particles reverse their magnetic state. Starting with a very diluted assembly of bistable particles, both conditions are fulfilled; however, as the packing fraction increases, each particle feels the interaction field which increases as the distance between particles is reduced. In this sense both bi-stability and the ability to reverse independently are susceptible to change as a consequence of any finite value of the interaction field. On one hand, bi-stability can be related to the strength of the coercive field of the individual particle, or to the height of the energy barrier that separates the two minimum configurations (+m and −m). On the other hand, the ability of the particles to rotate independently also depends on the value of the coercive field and the width of the intrinsic switching field distribution. So in both cases, the competition between the height of the intrinsic energy barrier of each particle and the magnitude of the interaction field determines if these conditions are fulfilled, and in this sense, there is no unique criterion but rather it will depend on the type of material and the main contributions to the energy.
In particular, the height of the energy barrier of the particles depends on the magnetocrystalline anisotropy. Since this contribution is intrinsic to each particle, it follows that the effects of the dipolar interaction are expected to become less relevant as the magnetocrystalline anisotropy of the individual particles increases [47–49]. In this sense, the magnetic hardness parameter [12] ![$\kappa =[\vert {K}_{\mathrm{MC}}\vert /(2 \pi {M}_{\mathrm{s}}^{2})]^{1/2}$](https://content.cld.iop.org/journals/0953-8984/25/22/226003/revision1/cm464223ieqn231.gif) provides a useful empirical parameter for the height of the energy barrier. In particular, the higher the value of κ, the higher the packing fraction attainable without loss of bi-stability or independent reversal. On the other limit, i.e. low values of κ, both the bi-stability and independent reversal are expected to be limited to low with and moderate packing fractions, as suggested by previous reports which show that magnetic percolation in assemblies takes place for packing fractions between 20 and 40% [50, 51].
provides a useful empirical parameter for the height of the energy barrier. In particular, the higher the value of κ, the higher the packing fraction attainable without loss of bi-stability or independent reversal. On the other limit, i.e. low values of κ, both the bi-stability and independent reversal are expected to be limited to low with and moderate packing fractions, as suggested by previous reports which show that magnetic percolation in assemblies takes place for packing fractions between 20 and 40% [50, 51].
5. Conclusion
In conclusion, mean field expressions have been derived for the demagnetizing field and the magnetostatic anisotropy field which include the magnetization dependent part of the interaction field for assemblies of magnetic particles with arbitrary inner and outer demagnetizing factors. Special emphasis was given to 2D arrays of nanomagnets with perpendicular magnetization, where the expressions for the demagnetizing field and total anisotropy field have been derived. The model was successfully tested using FMR and magnetometry measurements done on arrays of cylindrical nanowires, where the equivalence between the interaction field determined by each of these techniques was shown. This formalism provides a simple mean field framework to describe magnetostatic effects in a wide variety of magnetic assemblies and composites. Moreover, it shows the role played by the outer demagnetizing factor in the value and characteristics of the interaction field which could be used to fine tune the magnetic properties of the assembly or composite.
Acknowledgments
This work was partly supported by CONACYT México CB-105568, CB-177896 and 162651. J M Martínez Huerta and J De La Torre Medina also thank CONACYT for financial supports no. 201754 and Retención-166089, respectively.




