Abstract
Structure–property relations of monoclinic petalite, LiAlSi4O10, were determined by experiment and atomistic modeling based on density functional theory. The elastic stiffness coefficients were measured between room temperature and 570 K using a combination of the plate-resonance technique and resonant ultrasound spectroscopy. The thermal expansion was studied between 100 and 740 K by means of dilatometry. The heat capacity between 2 and 398 K has been obtained by microcalorimetry using a quasi-adiabatic calorimeter. The experimentally determined elastic stiffness coefficients were employed to benchmark the results of density functional theory based model calculations. The values in the two data sets agreed to within a few GPa and the anisotropy was very well reproduced. The atomistic model was then employed to predict electric field gradients, the lattice dynamics and thermodynamic properties. The theoretical charge density was analyzed to investigate the bonding between atoms.
Export citation and abstract BibTeX RIS
1. Introduction
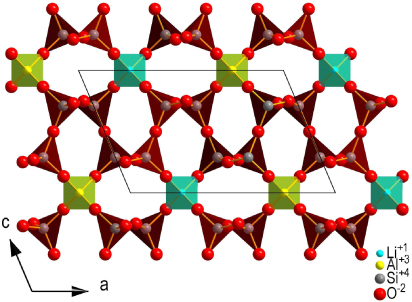
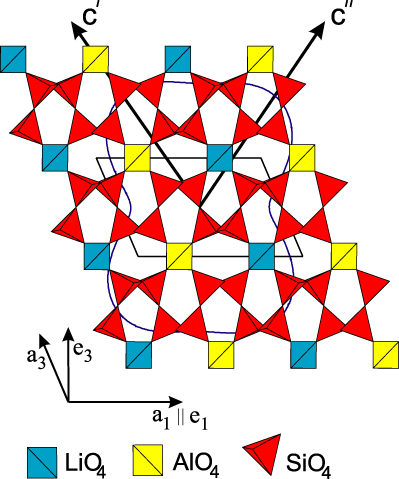
The crystal structure of petalite, LiAlSi4O10, a commercially important source of lithium, has been investigated several times in the past (e.g. Gossner and Mussgnug 1930, Zemann-Hedlik and Zemann 1955, Liebau 1961, Effenberger 1980, Tagai et al 1982) due to a controversy concerning its correct space group and structural details, such as the presence of 180° Si–O–Si bonds. The conclusion of the most recent structural studies was that petalite crystallizes in the monoclinic space group P2/a with lattice parameters a1 = 11.754 Å, a2 = 5.139 Å, a3 = 7.630 Å and α2 = 113.04° at room temperature with Z = 2 (figure 1) (Effenberger 1980, Tagai et al 1982).
Figure 1. Projection of the crystal structure of petalite along [010] which was determined at room temperature.
Download figure:
Standard imagePetalite exhibits an orthorhombic pseudo-symmetry (Tagai et al 1982), which is broken by the fully ordered distribution of Li+ and Al3+ cations.
The crystal structure can be classified as a three-dimensional framework of corner-connected TO4 tetrahedra, where T = Li,Al or Si. Alternatively, as there is perfect ordering of the cations on distinct crystallographic sites, petalite can be considered as a layer silicate. Following this interpretation, the structure is built up from folded [Si4O10] layers parallel to (001) which are linked by LiO4- and AlO4-tetrahedra.
While the structure of petalite is now well understood, its physical properties have not been studied in great detail. In the framework of a study to establish an internally consistent thermodynamic database for lithium containing minerals Fasshauer et al (1998) measured the bulk modulus in a multi-anvil cell and thermal expansion coefficients using high temperature x-ray diffraction, which they combined with an earlier calorimetric study of Hemingway et al (1984). The electric field gradient (EFG) at the Al-site has been determined by measuring the nuclear quadrupole resonance with a direct current superconducting quantum interference device (Connor et al 1990). These data have been used as a benchmark for Hartree–Fock calculations of EFGs in solids (Palmer and Blair-Fish 1994).
In order to better understand structure–property relations in petalite and to evaluate the reliability of the earlier results, we complement these earlier investigations by an experimental determination of the complete sets of elastic coefficients and thermal expansion coefficients of natural petalite in the temperature range 293–573 K and 100–740 K, respectively, by low temperature quasi-adiabatic calorimetry, and by density functional theory (DFT) based model calculations of the structure, compressibility, phonon density of states and electric field gradients.
2. Experimental details
2.1. Sample preparation and reference system
Large single crystals of natural petalite of gem quality were chosen for sample preparation. The lattice parameters a1 = 11.724(2) Å, a2 = 5.128(1) Å, a3 = 7.622(2) Å and α2 = 113.07(2)° obtained from x-ray diffraction experiments on a four-circle diffractometer equipped with graphite-monochromatized Mo Kα-radiation agree well with corresponding literature values (Effenberger 1980). Electron microprobe analyses revealed a nearly ideal chemical composition with traces of Na, K, Mn, Mg, Ca, Fe, Ni and Cr (in total less than 0.05% in weight). The density ρX = 2.412(2) g cm−3 calculated from sample composition and lattice parameters is in excellent agreement with ρb = 2.411(2) g cm−3 determined by the buoyancy method on large single crystals in pure water at 293 K. Single crystal structure determination and investigations using a polarizing microscope did not reveal any hint of twinning.
The physical properties reported here are referred to a Cartesian reference system with basis vectors ei, which are connected to the crystallographic basis vectors ai according to  ,
,  and e3 = (e1 × e2)
and e3 = (e1 × e2)  , where
, where 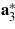 denotes the third basis vector of the reciprocal system. This non-standard setting was chosen to take advantage of the perfect cleavage plane parallel to (001) and of the orthorhombic pseudo-symmetry. The basis vectors
denotes the third basis vector of the reciprocal system. This non-standard setting was chosen to take advantage of the perfect cleavage plane parallel to (001) and of the orthorhombic pseudo-symmetry. The basis vectors  of the pseudo-orthorhombic unit cell are related to those of the monoclinic cell according to
of the pseudo-orthorhombic unit cell are related to those of the monoclinic cell according to  with the transformation matrix
with the transformation matrix

The transformation leads to  (Tagai et al 1982).
(Tagai et al 1982).
Rectangular parallelepipeds with edges parallel to ei and edge lengths li of about 6 mm were cut from large single crystals using a low-speed diamond saw and were polished on diamond disks (mesh 600 and 1200). The sample orientation was controlled by optical and x-ray methods. The deviation from the ideal orientation was kept below 0.4° and the deviation from plane parallelism of opposing faces was smaller than ± 2 μm. A measure of the quality of a sample with respect to geometrical errors is provided by the difference between the density, ρb, obtained by the buoyancy method in pure water at room temperature and the geometric density, ρg = M/(l1l2l3), calculated from sample mass M and dimensions li. These densities agree within 0.7% for all samples (table 2). Additionally, oriented plane-parallel plates with thicknesses between about 4 and 9 mm suitable for dilatometry and the plate-resonance technique were manufactured.
2.2. Dilatometry
The accurate determination of the temperature dependence of the elastic coefficients requires a correction for changes in sample dimensions and density due to thermal expansion effects. In order to determine the four independent coefficients of thermal expansion of monoclinic petalite, the temperature-induced strains were studied between 100 and 740 K on plane-parallel plates with plate normals parallel to ei and (e1 ± e3) using a commercial inductive gauge dilatometer type DIL402C from Netzsch equipped with a sample holder made of fused silica and thermocouples of type E. Each sample was measured at least three times with heating/cooling rates of 1 K min−1 under a He purge gas atmosphere. The dilatometer was first calibrated with standard samples made of fused silica.
2.3. Ultrasound spectroscopy
The elastic properties were studied with the aid of resonant ultrasound spectroscopy (RUS). A detailed description of the RUS technique can be found elsewhere (Leisure and Willis 1997, Migliori and Sarrao 1997).
For data collection at room temperature the samples were gently fixed between two piezoelectric ultrasound transducer plates (figure 2(a)). One transducer acts as an ultrasound generator and the other as an ultrasound detector. The force acting on the opposed corners of the sample was kept below 0.05 N. This ensured that the experimental setup fulfilled the conditions of a nearly freely vibrating body. Resonance spectra were collected at room temperature in the frequency interval of 100–1400 kHz with a resolution of 0.01 kHz using a network analyzer (HP 4394a from Agilent). In order to excite and detect all resonances four resonance spectra with the sample mounted in different orientations were taken for each sample. An example of an experimentally obtained resonance spectrum at room temperature is depicted in figure 2(b).
Figure 2. (a) RUS-device with a sample mounted for data collection (dimensions of the sample ca. 6.9× 5.1× 8.1 mm 3). (b) Part of an experimental resonance spectrum of a petalite sample at room temperature. The positions of calculated resonance frequencies are indicated by triangles.
Download figure:
Standard imageThe evaluation of the 13 independent elastic coefficients from the measured resonance frequencies was carried out by a non-linear least-squares procedure in which the observed resonance frequencies were compared to those calculated from the dimensions of the sample, the experimental density and the initial set of elastic coefficients which was derived by the plate-resonance technique (see below). The calculated resonance frequencies were obtained by solving a general eigenvalue problem, the rank of which was equal to the number of basis functions used for the development of the components of the displacement vector. In the non-linear least-squares refinement procedure the quantity
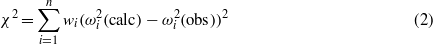
calculated for n circular eigenfrequencies with resonance frequencies fi = ωi/2π was minimized by varying the elastic coefficients of the sample. The wi are individual weights calculated by assuming experimental errors of ±0.1 kHz for each observed resonance frequency. In order to minimize errors due to truncation effects, up to 8775 normalized Legendre polynomials were used in the development of the displacement vector.
The convergence of the refinement procedure depends critically on the proper choice of the initial set of elastic coefficients. Therefore, an appropriate starting model was first determined by applying the plate-resonance technique (for details see Haussühl 2001) to plane-parallel plates of petalite with normals parallel to ei and ( − e1 + e3). These measurements were also required to overcome an intrinsic ambiguity in the interpretation of the RUS spectra that can appear if the point symmetry of the crystal is lower than the one of the sample shape. In the case of our rectangular parallelepipeds with edges parallel to ei two sets of elastic coefficients related by a non-crystallographic mirror plane perpendicular to e3 yield free resonances with different eigenvectors but identical frequencies.
The thermoelastic behavior of petalite was studied using a high temperature RUS-device built in-house (Haussühl et al 2011). The temperature stability inside the furnace (type 6.219.1-26 from Netzsch) achieved by a cascading temperature controller (EPC 900 from Eurotherm) was better than ± 0.5 K. The accuracy of the S-type thermocouple at the maximum temperature was better than ± 5 K. For the high temperature RUS measurements the samples were slightly clamped at opposite corners between the ends of two horizontally arranged corundum ceramic rods which acted simultaneously as ultrasonic wave guides. The ultrasound generator and detector were mounted on the cold ends of the corundum rods outside the furnace. For signal generation and detection a network analyzer (HP4194a from Agilent) in combination with a high-speed signal amplifier (type 4400 from NF-electronics) was employed. Resonance spectra in the frequency range 100 and 1400 kHz were collected between 293 and 573 K in steps of 20 K in air. At each temperature step the sample was first allowed to equilibrate for at least 30 min before the resonance spectrum was recorded. After extraction of the resonance frequencies the elastic coefficients at each temperature were refined using the set of elastic coefficients evaluated at the previous temperature step as initial values. Further, changes of sample dimensions li(T) = li(T0)(1 + εii(T)) and density
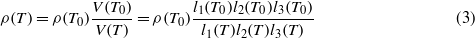
due to thermal expansion effects were taken into account. T0 = 293 K is the reference temperature and εii denotes the strain along ei as observed by dilatometry.
2.4. Microcalorimetry
The heat capacity of petalite has been obtained in the range from 2 to 395 K on a single crystal of about 15 mg in weight using a Quantum Design PPMS system. Data sets were collected at 120 temperatures where the temperature difference between subsequent steps was increased logarithmically from low to high temperatures. At each temperature, 3 responses to a heat pulse were measured and analyzed by the MultiVu software under which the measurements were run.
3. Computational details
DFT based calculations were performed with academic and commercial versions of the CASTEP program (Clark et al 2005, CASTEP User Guide 2008, Milman et al 2000) using a generalized gradient approximation in the PBE (Perdew et al 1996) and the PBESOL formulation (Perdew et al 0000). For all calculations, ultrasoft pseudopotentials from the CASTEP data base were generated 'on the fly', with 3, 6, 3 and 4 valence electrons for Li, O, Al and Si, respectively. The maximum cutoff energy of the plane waves was 610 eV. In addition to the cutoff energy, the quality of the calculations was determined by the density of the grid of k-points in the Brillouin zone. Here distances between the points were less than 0.03 Å−1. The wave vectors for the sampling points were chosen according to the scheme proposed by Monkhorst and Pack (1976). Full geometry optimization calculations were performed. Structures were considered to be converged when the largest residual component of the stress tensor was less than 0.02 GPa and the largest residual force acting on an atom was less than 0.01 eV Å−1. The elastic stiffness coefficients were obtained as the proportionality constants between the applied strains and the resultant stresses. Strain patterns were imposed with several magnitudes up to a distortion of 0.2% of the lattice parameters, and after geometry optimization of the internal parameters the resultant stresses were computed. Electric field gradients were computed after the geometry optimizations according to the theory developed by Pickard and Mauri (2001). The phonon density of states was obtained from finite displacement calculations. The present calculations are restricted to the athermal limit, in which temperature effects and zero-point motions were neglected.
4. Experimental results
4.1. Thermal expansion
While the temperature-induced strains εii could directly be studied on the rectangular parallelepipeds, the component ε13 = (ε' − ε'')/2 of the strain tensor was derived from the longitudinal strains ε' and ε'' observed along e1 + e3 and e1 − e3, respectively. The thermal expansion of petalite is highly non-linear (figure 3); thus, fourth order polynomials of the type
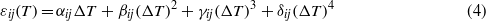
with ΔT = T − T0 are required for a proper approximation of the strains εij over the entire investigated temperature range. T0 = 293 K denotes the reference temperature and αij, βij, γij and δij are the corresponding coefficients of linear, quadratic and higher order thermal expansion. With less than 0.1% the uncertainties of the fit parameters are rather small (table 1). In fact, the reproducibility of the linear thermal expansion coefficients αij at room temperature is of the order of ± 3%.
Figure 3. Temperature-induced strains εij of petalite as observed by dilatometry.
Download figure:
Standard imageTable 1. Thermal expansion coefficients of petalite. The temperature evolutions of the four independent components of the strain tensor are described according to εij = αij(T − T0) + βij(T−T0)2 + γij(T−T0)3 + δij(T−T0)4 with T0 = 293 K. Standard deviations in the last digit as derived from the least-squares procedure are given in parentheses.
| ij | αij(10−6 K−1) | βij(10−9 K−2) | γij(10−12 K−3) | δij(10−15 K−4) |
|---|---|---|---|---|
| 11 | 0.974(1) | 6.251(1) | −14.36(1) | 14.77 (1) |
| 22 | 11.689(1) | 10.918(2) | −17.07(2) | 4.89(3) |
| 33 | −7.351(1) | 7.699(2) | −6.48(2) | 8.46(3) |
| 13 | 0.244(1) | −0.85(1) | 1.72(1) | 4.76(1) |
4.2. Elastic properties
A total of three different samples were investigated with resonant ultrasound spectroscopy at room temperature. All observed resonances could be unambiguously identified and were used in the non-linear least-squares procedures. The fully converged sets of elastic coefficients are presented in table 2. In all cases an excellent match between calculated and observed resonance frequencies could be achieved as indicated by the low average and maximum values of Δfi = |fi(calc) − fi(obs)|. This reflects the high precision of the RUS technique. The corresponding longitudinal and shear stiffnesses of the different samples agree within 0.3%. Deviations of up to 0.5 GPa are observed for the small coupling coefficients c15 and c35.
Table 2. Elastic coefficients cij (GPa) of petalite at 293 K. The standard deviations of the experimental cij as derived from the covariance matrix of the fully converged non-linear least-squares refinements of the elastic coefficients are given in parentheses. The standard deviations of the cij calculated by DFT are obtained from the numerical error of the fit used to derive the cij from stress–strain relations. Abbreviations: li (mm), edge length; ρg (g cm−3), geometric density; wR (10−3), the weighted residual of the converged refinement. Δfav (kHz) and Δfmax (kHz) are the average and maximum differences between measured and calculated frequencies of the eigenmodes.
| Sample | 1 | 2 | 3 | Average | DFT |
|---|---|---|---|---|---|
| c11 | 91.73(5) | 91.43(4) | 91.27(4) | 91.5(2) | 93.9(3) |
| c22 | 93.04(8) | 93.09(7) | 92.98(6) | 93.04(4) | 97(3) |
| c33 | 153.27(9) | 153.11(7) | 151.09(8) | 152.5(9) | 157.1(8) |
| c44 | 29.44(3) | 29.38(2) | 29.30(2) | 29.37(6) | 31.4(2) |
| c55 | 69.84(9) | 69.80(7) | 69.37(9) | 69.7(2) | 70.7(8) |
| c66 | 52.88(7) | 52.70(5) | 52.63(5) | 52.7(1) | 56.0(6) |
| c12 | −0.01(2) | 0.0(2) | 0.2(2) | 0.1(1) | 2.7(2) |
| c13 | 69.39(4) | 69.18(3) | 68.40(3) | 69.0(4) | 76(1) |
| c23 | 6.2(2) | 6.5(2) | 6.7(2) | 6.5(2) | 10(3) |
| c15 | −1.0(4) | −0.4(3) | −0.7(3) | −0.7(2) | −1.0(3) |
| c25 | −1.1(7) | −1.3(4) | −2.1(4) | −1.5(4) | −0.7(4) |
| c35 | −0.4(5) | −0.9(4) | −0.8(5) | −0.7(2) | −1.4(1) |
| c46 | 2.5(1) | 2.5(1) | 2.3(1) | 2.4(1) | −2.0(1) |
| l1 | 6.664(2) | 6.928(2) | 5.315(2) | ||
| l2 | 6.714(2) | 5.139(2) | 6.690(2) | ||
| l3 | 6.225(2) | 8.100(2) | 7.393(2) | ||
| ρg | 2.393(2) | 2.395(2) | 2.392(2) | ||
| No. fobs | 106 | 154 | 131 | ||
| Δfav | 0.30 | 0.16 | 0.36 | ||
| Δfmax | 1.04 | 0.61 | 1.24 | ||
| wR | 0.74 | 0.36 | 0.73 |
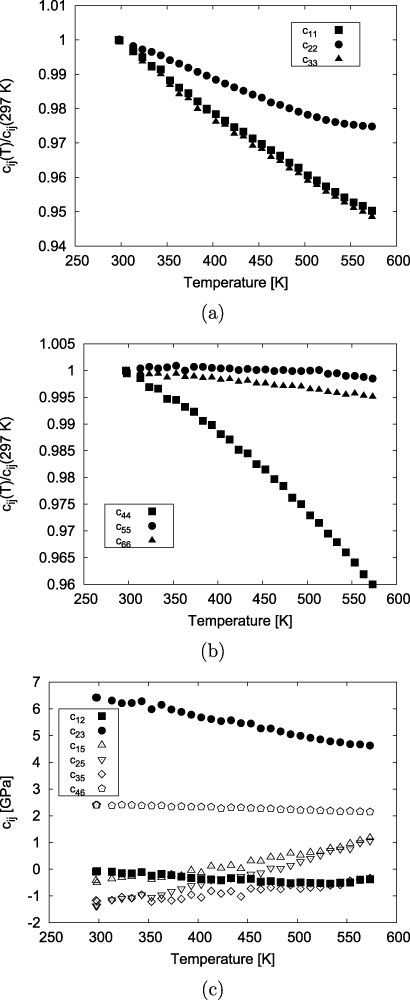
Between room temperature and 573 K the temperature evolution of the elastic coefficients was fully reversible in successive heating and cooling runs within experimental error (figure 4). With the exception of c55 all principal elastic coefficients cii exhibit negative temperature coefficients ∂cii/∂T at room temperature. However, most of the principal stiffnesses display a distinct non-linear softening with increasing temperature, which can be best approximated by second order polynomials (table 3).
Figure 4. Temperature evolution of the elastic stiffnesses cij of petalite.
Download figure:
Standard imageTable 3.
Temperature coefficients of elastic moduli of petalite as derived by polynomial regressions of type  with reference temperature T0 = 295 K from experimental data obtained on sample 2 (cf table 2). The numbers in parentheses are the uncertainties of the last digit as derived from the standard deviations of the corresponding fit parameter. The thermoelastic coefficients Tij = ∂logcij/∂T are for 295 K.
with reference temperature T0 = 295 K from experimental data obtained on sample 2 (cf table 2). The numbers in parentheses are the uncertainties of the last digit as derived from the standard deviations of the corresponding fit parameter. The thermoelastic coefficients Tij = ∂logcij/∂T are for 295 K.
| ij |
 (GPa) (GPa) |
 (MPa K−1) (MPa K−1) |
 (kPa K−2) (kPa K−2) |
 (10−4 K−1 ) (10−4 K−1 ) |
|---|---|---|---|---|
| 11 | 91.30(2) | −19.9(3) | +11.7(9) | −2.2 |
| 22 | 93.03(2) | −12.2(4) | +11.2(13) | −1.3 |
| 33 | 152.85(4) | −35.7(6) | +26(2) | −2.3 |
| 44 | 29.31(1) | −2.5(1) | −6.2(2) | −0.85 |
| 55 | 69.73(1) | +0.6(1) | −3.7(5) | +0.09 |
| 66 | 52.60(1) | −0.6(1) | −1.2(3) | −0.11 |
| 12 | −0.03(2) | −3.8(4) | +7.9(14) | +1267 |
| 13 | 69.07(2) | −23.7(4) | +16.0(15) | −3.4 |
| 23 | 6.47(3) | −6.9(5) | 0(2) | −11 |
| 15 | −0.44(4) | +2.3(7) | +12(2) | −52 |
| 25 | −1.32(3) | +5.8(5) | +10(2) | −44 |
| 35 | −1.16(4) | +1.1(7) | +6(3) | −9.5 |
| 46 | 2.41(1) | −0.6(1) | −1.3(4) | −2.5 |
4.3. Microcalorimetry
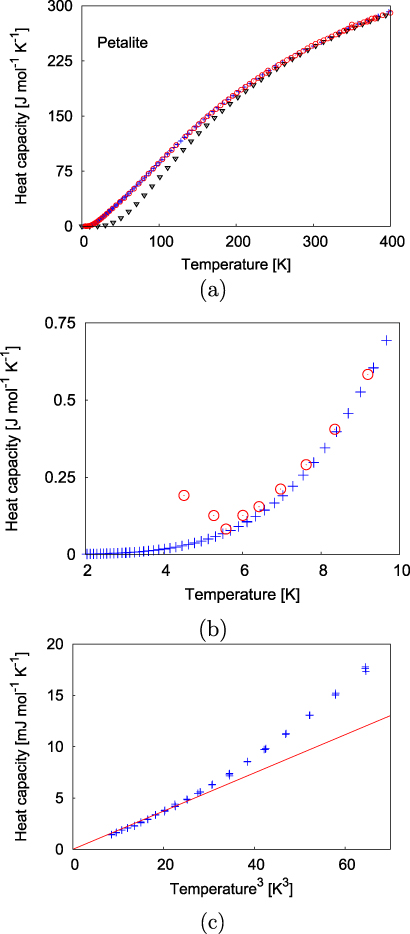
The experimentally obtained heat capacity is shown in figure 5, where it is compared to data obtained by Hemingway et al (1984) There is no anomaly in the temperature range investigated, i.e. there is no indication of a phase transition. The agreement between the data obtained here on a very small sample of ≈ 20 mg are, generally, in excellent agreement with the data obtained on a sample weighing 306 g by Hemingway et al (1984). In effect, the data sets are indistinguishable at temperatures T > 10 K. At lower temperatures, there are small discrepancies. The data obtained at the lowest temperatures accessible to Hemingway et al (1984) show an incorrect temperature dependence, in that the heat capacity decreases with increasing temperature. In our data, there is no such anomaly and we are confident that our low temperature data are more reliable than those presented by Hemingway et al (1984). At low temperatures (T < 3 K), the heat capacity depends linearly on T3 (figure 5). Using the low temperature approximation to the Debye model,

where n = 16 is the number of atoms per formula unit, R = 8.314 462 J (mol K)−1, and neglecting the difference between cv and cp, the linear dependence gives a Debye temperature Θcalorim of 551 K. Petalite differs from other compounds we have investigated in that significant deviations from the T3-dependence already begin at 3 K, while for other silicates and related compounds the linear dependence is observed up to 5 or 6 K. As the analysis relies on a T3-dependence, this is a significant difference. Using the heat capacity data, the molar enthalpy of formation (△fH° = 38 378 ± 15 J mol−1) and the standard molar entropy (S° = 233.9 ± 0.2 J K−1 mol−1) at 298.15 K were calculated. The values agree very well with the previous result (S° = 233.2 ± 0.6 J K−1 mol−1; Hemingway et al 1984).
Figure 5. (a) Experimentally (crosses and circles) and theoretically (triangles) determined heat capacity of petalite. The crosses represent data obtained here, while the circles are data from Hemingway et al (1984). (b) The experimental data sets coincide at temperatures above 8 K, while at lower temperatures there is appreciable scatter in the older data. There is no indication of a phase transition in the temperature region from 2–400 K. (c) At low temperatures the temperature dependence of the heat capacity is proportional to T3 (straight line).
Download figure:
Standard image5. Results from the DFT calculations
The lattice parameters obtained from the geometry optimizations (atheo = 11.8345 Å, btheo = 5.1711 Å, ctheo = 7.6521 Å, βtheo = 113.12°) are in very good agreement with the experimental results by Effenberger (1980). Bond distances and bond angles are described equally well, e.g. for the tetrahedrally coordinated Si(1). Effenberger (1980) obtained two short bonds with Si(1)–O(1) =1.596(1) Å and Si(1)–O(4) =1.598(1) Å, where our calculations give a distance of 1.606 Å, and two longer bonds with Si(1)–O(3) =1.613(1) Å and Si(1)–O(5) =1.615(1) Å, where we obtain 1.615 and 1.618 Å, respectively. Hence, the ground state structure is well described. The elastic stiffness coefficients obtained from the stress–strain relations are given in table 2, where they are compared to our experimentally obtained results. The model gives slightly too large values for all six main diagonal elastic stiffness coefficients cii, where the differences are a few per cent and a few GPa. The bulk modulus derived from the model calculations is 49(1), 4 GPa larger than the experimental value. Part of these discrepancies is due to the influence of temperature, as the experimental values were obtained at ambient conditions, while the theoretical results refer to the athermal limit. However, the overall elastic behavior of petalite is very well reproduced, with a similar accuracy to that we have obtained for orthorhombic sillimanite and andalusite (Winkler et al 2001) or orthorhombic Bi2Ga4O9 (Schreuer et al 2006).
The elastic stiffness coefficients can be used to obtain mean sound velocities which can then be employed to compute a Debye temperature Θelastic (Robie and Edwards 1966):
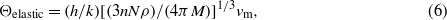
where h and k are the Planck and Boltzmann constants, n is again the number of atoms per formula unit, N is Avogadro's number, M is the formula weight and vm is the mean sound velocity, respectively. A rough estimation of the mean sound velocity vm was computed according to the approach described by Robie and Edwards (1966):
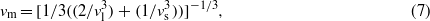
where vl and vs are the longitudinal and shear sound velocities, respectively, using the isotropic elastic values  and
and  (table 5) of the Voigt–Reuss averaging. This calculation yielded Θelastic = 590 K, which is in reasonable agreement with the one obtained from calorimetry, Θcalorim = 551 K. While for many metals often a better agreement between these two values is obtained, there are cases, even for high symmetry compounds, where Θelastic differs by several tens of kelvin from Θcalorim (Alers and Neighbours 1959).
(table 5) of the Voigt–Reuss averaging. This calculation yielded Θelastic = 590 K, which is in reasonable agreement with the one obtained from calorimetry, Θcalorim = 551 K. While for many metals often a better agreement between these two values is obtained, there are cases, even for high symmetry compounds, where Θelastic differs by several tens of kelvin from Θcalorim (Alers and Neighbours 1959).
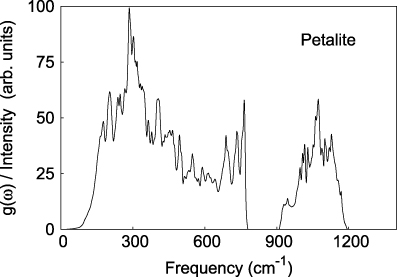
From the computed phonon density of states (figure 6) we can obtain thermodynamic properties such as the heat capacity (figure 5). At temperatures T > 200 K the computed heat capacities are in excellent agreement with the experimentally determined values while at lower temperatures, the computed heat capacity is significantly lower. We have ensured by comparing several calculations that this discrepancy is not due to an insufficient sampling of the dispersion relations. Also, the low frequency regime of the density of states does not show any artifacts caused by coarse sampling. This implies that the harmonic model misses some low frequency dynamics, such as a cation rattling in a cage, low frequency rigid unit modes, or a hopping between two sites. This will be discussed below.
Figure 6. Computed phonon density of states of petalite obtained from DFT calculations.
Download figure:
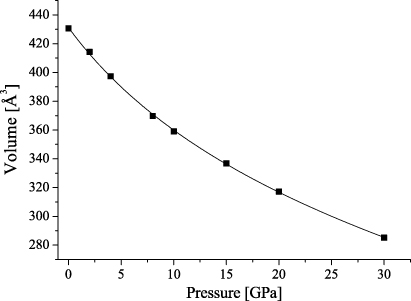
Standard imageIn addition to the computation of the bulk modulus from the elastic stiffness coefficients, we have also used a fit of a third order Birch–Murnaghan equation of state to unit cell volumes calculated for applied pressures up to 30 GPa to obtain B (figure 7). The fit of the pressure dependence of the unit cell volume with a third order Birch–Murnaghan equation of state yielded a bulk modulus of 43(1) GPa and a pressure derivative of the bulk modulus of 2.88(7). It is not uncommon that bulk moduli computed from finite strains and compression data differ by a few GPa (e.g. Hantsch et al 2005), and this is the case here as well. An average of the three values obtained in the present study gives a preferred value of B = 45.5 GPa, identical to the experimentally determined value.
Figure 7. The pressure dependence of the unit cell volume of petalite was obtained from DFT calculations. The line represents a fit with a third order Birch–Murnaghan equation of state.
Download figure:
Standard imageAs the atomistic model calculations are based on the self-consistent determination of the electron density, it is possible to extract EFGs. Experimental values are available only for the Al-nuclei (Connor et al 1990), but an earlier study by Palmer and Blair-Fish (1994) provides the opportunity to compare different theoretical approaches. The results of the EFG calculations are listed in table 4, where they are compared to experiment and earlier theoretical results.
Table 4. Electric field gradients, given by qzz and the asymmetry parameter η from experiment (Connor et al 1990) and theory and Mulliken populations. The experimental data are from Connor et al (1990). The values labeled with 'theo⋆' are from Palmer and Blair-Fish (1994). The labels 'fixed' and 'optimized' refer to calculations without and with full geometry optimizations, respectively. The former indicates that the structural parameters of Tagai et al (1982) were used. The atom labeling is that of Tagai et al (1982).
| Atom | Reference | qzz (au) | η | Mulliken population |
|---|---|---|---|---|
| Al | exp | 0.47(1) | ||
| theo⋆ | −0.1578 | 0.53 | 11.13 | |
| theo fixed | −0.1590 | 0.48 | 11.16 | |
| theo optimized | −0.1613 | 0.36 | 11.16 | |
| Li | theo⋆ | −0.0055 | 0.38 | 2.04 |
| theo fixed | −0.0025 | 0.22 | 1.87 | |
| theo optimized | −0.0027 | 0.51 | 1.88 | |
| Si(1) | theo⋆ | −0.1398 | 0.19 | 12.49 |
| theo fixed | −0.1297 | 0.19 | 11.70 | |
| theo optimized | −0.1265 | 0.25 | 11.70 | |
| Si(2) | theo⋆ | −0.1590 | 0.25 | 12.50 |
| theo fixed | −0.1641 | 0.24 | 11.71 | |
| theo optimized | −0.1351 | 0.23 | 11.71 | |
| O(1) | theo⋆ | +1.1782 | 0.02 | 8.81 |
| theo fixed | +0.9351 | 0.03 | 9.20 | |
| theo optimized | +0.9575 | 0.02 | 9.19 | |
| O(2) | theo⋆ | +1.1651 | 0.06 | 8.80 |
| theo fixed | +0.9346 | 0.07 | 9.19 | |
| theo optimized | +0.9354 | 0.06 | 9.19 | |
| O(3) | theo⋆ | +1.1782 | 0.16 | 8.79 |
| theo fixed | +0.9136 | 0.20 | 9.18 | |
| theo optimized | +0.9211 | 0.16 | 9.18 | |
| O(4) | theo⋆ | +0.9563 | 0.34 | 9.03 |
| theo fixed | +0.6456 | 0.31 | 9.25 | |
| theo optimized | +0.6344 | 0.32 | 9.26 | |
| O(5) | theo⋆ | — | — | 8.78 |
| theo fixed | +0.8986 | 0.22 | 9.18 | |
| theo optimized | +0.9028 | 0.18 | 9.18 | |
| O(6) | theo⋆ | — | — | 9.03 |
| theo fixed | +0.6086 | 0.37 | 9.26 | |
| theo optimized | +0.6254 | 0.37 | 9.26 |
Palmer and Blair-Fish (1994) only gave qzz values for O(1)–O(4), while in the structure of petalite, when described in space group P2/a, there are six symmetrically independent oxygen positions. There are three significant differences between the approach used by Palmer and Blair-Fish (1994) and the one here. The former study employs Hartree–Fock exchange and no correlation as implemented in the CRYSTAL-92 code, while we use a generalized gradient approximation within density functional theory. The former study employs an atomic basis set, while we use a combination of pseudopotentials and plane waves. Finally, Palmer and Blair-Fish (1994) use the published coordinates, while we compute the EFGs both before and after geometry optimizations. As there are no transition metal ions in the structure of petalite, it is unlikely that neglecting correlation effects will have a large effect. In models based on atomic orbitals, the results of a calculation of the EFGs very strongly depend on the basis set (Palmer and Blair-Fish 1994), and hence require a judicious, experience based choice. In contrast, the numerical convergence of models based on plane waves is easily controlled. In general, EFGs are very sensitive to small changes in structural parameters (Winkler et al 1996, Hantsch et al 2005). As can be inferred from table 4, the three theoretical data sets (from Palmer and Blair-Fish 1994, for the fixed and geometry-optimized structures) all agree with respect to the sign of all values of qzz. The difference between the results presented by Palmer and Blair-Fish (1994) and those obtained here for the same geometry is very small for Al, Li and Si ( ≤ 0.01 au) and there is a consensus that the value for Li is very small in comparison to all other atoms. These differences are similar to the experimental error. For O(1)–O(4) the differences are slightly larger ( ≈ 0.25–0.30 au), and the values of Palmer and Blair-Fish (1994) are all systematically larger than those obtained here.
Similarly, the agreement between the asymmetry parameters is generally very good between the three theoretical data sets, with differences between the three data sets smaller than 0.05. The value computed here for η(Al) with the structural parameters of Tagai et al (1982) is in excellent agreement with the one available data point (Connor et al 1990). There is one notable exception, namely η for Li, where the values range from 0.22 to 0.51, but it is not obvious what causes the difference. From the data presented here, there is a clear correlation between η and qzz for the oxygen atoms, as the two oxygen atoms O(4) and O(6) which have significantly smaller qzz than the other four oxygen atoms have also significantly more asymmetric EFGs.
From a structural point of view, the O(4) and O(6) oxygen atoms differ from the other oxygens in that they are part of all coordination polyhedra (i.e. there are Al–O(4, 6), Li–O(4, 6) and Si(1)–O(4) and Si(2)–O(6) bonds) while the O(1), O(2), O(3) and O(5) atoms only bound to Si-atoms. The calculations therefore confirm the intuitive assumption that bonds such as Al–O(4, 6)-Si and Li–O(4, 6)–Si lead to an increased asymmetry of the EFG at the oxygen site in contrast to Si–O–Si bonds.
Considering the significant discrepancies in the underlying computational models, the agreement between the earlier calculations and the present results is very satisfactory, and clearly no open question remains regarding the signs of the qzz, which cannot be determined experimentally. While experiment probably cannot be used to benchmark the accuracy of the results for Li, Al and Si, as the differences between the models are too small, it would be of interest to determine which of the two approaches is more reliable for the prediction of the EFGs of oxygen atoms.
In table 4 we also compare the atomic Mulliken populations obtained here with those obtained by Palmer and Blair-Fish (1994). While the computation of Mulliken populations is straightforward with approaches based on atomic orbitals, plane wave based calculations require a projection of the plane wave states on a localized basis set (Segall et al 1996). For this projection, typically a minimal basis is employed, while Palmer and Blair-Fish (1994) used a more complex basis set for their calculations. Hence, some differences are to be expected. Here again the three theoretical data sets are in very satisfactory agreement, and typically the differences are less than 0.2e−. In the present study, we have also calculated the charge accumulation along cation–anion bonds, and we find that, as expected, the Si–O bond is the most covalent, with a bond population of 0.53e− Å−3. Al–O bonds are slightly less covalent, with bond populations of 0.44e− Å−3. There is no charge accumulation along Li–O contacts, so the interactions within the Li–O tetrahedra are purely electrostatic.
6. Discussion
6.1. Elastic properties at room temperature
The elastic behavior of petalite exhibits a pronounced anisotropy as expressed by the ratio c'(max)/c'(min) ≈ 2.0 of the maximum and minimum of the longitudinal elastic stiffness c'(u) = uiujukulcijkl, where ui are direction cosines (cf table 5). The two nearly equivalent local maxima of c'(u) within the (010) plane, c' = 172.5 GPa along 0.5670e1 + 0.8237e3 and c'' = 168.8 GPa along − 0.5680e1 + 0.8231e3 enclosing angles of − 34.6° and + 34.5° with the e3-axis, give rise to a nearly orthorhombic pseudo-symmetry of the corresponding representation surface (figures 9(a)–(c)). Figure 8 shows that the directions of these extreme values almost coincide with the orientations of Si–O–Si-bonds. Within the plane perpendicular to e3 the longitudinal elastic stiffness reaches only about 50% of its maximum value and behaves nearly isotropically.
Figure 8. Projection of the crystal structure of monoclinic petalite along the two-fold axis and outline of the representation surface of the longitudinal elastic stiffness. c' and c'' are the directions of the nearly equivalent maxima of the longitudinal elastic stiffness within the (010) plane.
Download figure:
Standard imageFigure 9. Representation surfaces of ((a)–(c)) the longitudinal elastic stiffness (in GPa) and of the longitudinal effects of ((d)–(f)) the deviations from Cauchy relations (in GPa), (g)–(i) the ∂cij/∂T (in 10−4 K−1) and (j)–(l) the thermal expansion (in 10−6 K−1). View along e1 (upper row), e2 (middle row) and e3 (lower row). Only the representation surface of the temperature coefficients of the elastic coefficients shows a significant deviation from the orthorhombic pseudo-symmetry.
Download figure:
Standard imageTable 5.
Comparison of elastic properties of selected lithium silicates and α-quartz. ρ density in g cm−3, MW molar weight in g mol−1, c'(max)/c'(min) ratio of maximum and minimum longitudinal elastic stiffness, 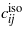 aggregate elastic coefficients in GPa (average of Voigt and Reuss model),
aggregate elastic coefficients in GPa (average of Voigt and Reuss model),  eigenvalues of deviations from Cauchy relations in GPa, g mean deviation from Cauchy relations, B (Reuss model) and C bulk modulus and mean elastic stiffness in GPa, Sexp and Scalc experimental and calculated elastic S-value in 10−20 N m.
eigenvalues of deviations from Cauchy relations in GPa, g mean deviation from Cauchy relations, B (Reuss model) and C bulk modulus and mean elastic stiffness in GPa, Sexp and Scalc experimental and calculated elastic S-value in 10−20 N m.
| Mineral | α-quartz | Petalite | β-eucryptite | Spodumene |
|---|---|---|---|---|
| Composition | SiO2 | LiAlSi4O10 | LiAlSiO4 | LiAlSi2O6 |
| Reference | Heyliger et al (2003) | This work | Haussühl et al (1984) | Sondergeld et al (2006) |
| Si:Al:Li | 1:0:0 | 4:1:1 | 1:1:1 | 2:1:1 |
| ρ | 2.650 | 2.411 | 2.352 | 3.182 |
| MW | 60.09 | 306.28 | 126.01 | 186.10 |
| c'(max)/c'(min) | 1.75 | 2.0 | 1.42 | 1.43 |

|
97.1 | 107.8 | 164.5 | 259.5 |

|
8.0 | 20.9 | 73.1 | 87.7 |
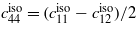
|
44.6 | 43.5 | 45.7 | 85.9 |
| Biso | 37.7 | 49.9 | 103.5 | 145.0 |
| B | 37.4 | 45.5 | 102.7 | 143.9 |
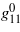
|
−46.3 | −53.1 | +26.0 | −12.4 |

|
−46.3 | −22.4 | +26.0 | −4.2 |

|
−33.7 | −0.7 | +22.1 | +11.4 |
| g = (g11 + g22 + g33)/3 | −42.1 | −26.6 | +24.7 | −1.1 |
| C | 52.0 | 62.9 | 96.1 | 146.5 |
| Sexp | 195 | 1338 | 855 | 1423 |
| Scalc | 195 | 1154 | 860 | 1459 |
A deeper insight into the nature of the bonding interactions in crystals is provided by the deviations from Cauchy relations, a second-rank tensor invariant of the elasticity tensor with components gmn = cijkleikmejln/2, where eijk are the components of the Levi-Civitá tensor (Haussühl 1967, 2007, Schreuer and Haussühl 2005). In crystals with strong ionic bonds, and particularly in those containing aspherical or highly polarizable constituents, the transverse interaction coefficients usually dominate considerably over the corresponding shear stiffnesses, resulting in positive deviations from Cauchy relations. Strong covalent or other bonds with preferential orientation give rise to large shear stiffnesses and therefore cause opposite effects. For example, the relatively high covalency of the Si–O bond leads to strongly negative deviations from Cauchy relations in α-quartz (table 5). In contrast, the eigenvalues 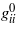 of the (gmn) tensor of β-eucryptite, LiAlSiO4, are all positive because here 1/3 of the tetrahedral positions are occupied by Li, where the Li–O interactions have a predominantly ionic character.
of the (gmn) tensor of β-eucryptite, LiAlSiO4, are all positive because here 1/3 of the tetrahedral positions are occupied by Li, where the Li–O interactions have a predominantly ionic character.
Petalite presents a case intermediate between β-eucryptite and quartz. As has been discussed before, the bond populations obtained from the DFT calculations clearly show the covalent character of the Si–O and Al–O bonds, while there is no charge accumulation along Li–O contacts, so the interactions within the Li–O tetrahedra are purely electrostatic. The ratio of predominantly covalently bonded (Si,Al)O4-tetrahedra to ionic LiO4-tetrahedra is therefore 5:1 in petalite, while it is 1:0 in quartz and 2:1 in β-eucryptite, respectively. One can therefore expect a value of the mean deviation form Cauchy relations g for petalite which is intermediate between those of quartz and β-eucryptite. This is indeed the case (table 5).
The bulk modulus derived here from experiment and theory is about 38% larger than B = 33 GPa derived by Fasshauer et al (1998) from compressibility data, to which a Murnaghan equation of state was fitted. The latter data set was obtained in a very small pressure interval from 1.2–5.7 GPa only and no detailed information on the data analysis is presented. Due to the limited pressure range, the uncommonly small value derived for the pressure derivate, B' = 0.1, by Fasshauer et al (1998) will certainly have a very large error associated with it. We therefore are confident that the data presented here (B = 45 GPa, B' ≈ 3) are superior to the value used by Fasshauer et al (1998). We note that other values employed in the thermodynamic analysis of Li-bearing systems by Fasshauer et al (1998) have also been superseded by new results, which leads us to conclude that this internally consistent database may be of limited accuracy.
It is well established that the bulk modulus of quartz is uncommonly small for silicates, and that this is due to the presence of rigid unit modes, which permit a compression of the structure by a cooperative rotation of quasi-rigid tetrahedra. The bulk modulus of petalite is similar to that of α-quartz, and hence it is likely that in this structure deformations by small changes of O–T–O bond angles are also possible. In β-eucryptite and spodumene the larger number of cation–anion contacts and, respectively, the much higher packing density lead to considerably stiffer crystal structures.
A detailed comparison of the elastic properties of crystal species belonging to different point symmetry groups can be achieved by comparing further scalar invariants of the elasticity tensor, such as the mean elastic stiffness C = (c11 + c22 + c33 + c12 + c13 + c23 + c44 + c55 + c66)/9. In order to take into account the effect of packing, Haussühl (1993) introduced the elastic S-value as the product S = CVm of the mean elastic stiffness and the molecular volume Vm = Mw/(NAρ), where Mw is molar weight, NA is Avogadro's number and ρ is the density. Under the assumption that the interactions between cations and surrounding anions are similar in a compound X and in its stable constituents Xi the S-value of X can be decomposed into additive contributions S(Xi) according to S(X) = ∑S(Xi). This quasi-additivity rule holds for many ionic crystals and even for many silicates to within about 10% (Haussühl 1993, Schreuer and Haussühl 2005). For petalite the quasi-additivity rule leads to

where S(Li2O) = 228 × 10−20 N m,  N m and has been derived for a hypothetical compound with Al in tetrahedral coordination (Schreuer and Haussühl 2005). SiO2 crystallizes in a number of modifications whose S-values differ by more than a factor of 5 (Schreuer and Haussühl 2005). In the case of β-eucryptite, the use of S(quartz) = 195 × 10−20 N m is obvious, since its crystal structure can be considered a derivative of the β-quartz structure. A reasonable agreement between the experimental and calculated S-value of petalite can be achieved if the S-value of α-quartz is used for S(SiO2). In contrast, the almost closed-packed arrangement of oxygen atoms in spodumene requires the use of S(coesite) (table 5).
N m and has been derived for a hypothetical compound with Al in tetrahedral coordination (Schreuer and Haussühl 2005). SiO2 crystallizes in a number of modifications whose S-values differ by more than a factor of 5 (Schreuer and Haussühl 2005). In the case of β-eucryptite, the use of S(quartz) = 195 × 10−20 N m is obvious, since its crystal structure can be considered a derivative of the β-quartz structure. A reasonable agreement between the experimental and calculated S-value of petalite can be achieved if the S-value of α-quartz is used for S(SiO2). In contrast, the almost closed-packed arrangement of oxygen atoms in spodumene requires the use of S(coesite) (table 5).
6.2. Temperature dependence of elastic coefficients
Among the thermo-mechanical properties investigated here only the fourth-rank tensor (∂cij/∂T) of the temperature coefficients of the elastic coefficients shows significant deviations from the orthorhombic pseudo-symmetry (figures 9(g)–(i)). In particular, the two local maximum values, c' and c'', within the (010) plane have different temperature dependences. In conjunction with the negative thermal expansion along e2 (see below) this probably is indicative of a cooperative rotation of coordination polyhedra.
Remarkable features are the pronounced anisotropy and the non-linearity of the temperature dependence of the elastic stiffnesses (figure 4). For example, between room temperature and 570 K, c44 softens by about 4% whereas the shear stiffnesses c55 and c66 are nearly independent of temperature. Regarding the sign of their second derivatives with respect to temperature the principal elastic coefficients of petalite can be divided into two groups (table 3). With ∂2cij/∂T2 < 0 the shear stiffnesses develop normally with increasing temperature. However, the longitudinal stiffnesses and the transverse interaction coefficients all show ∂2cij/∂T2 > 0, i.e. the softening of these elastic coefficients reduces with increasing temperature. An understanding of this observation would require ultrasound and diffraction measurements at higher temperatures, which are, however, difficult due to an often observed spontaneous cleaving of the petalite samples at elevated temperatures.
Petalite shows no observable dissipation phenomena in the investigated temperature and frequency range. This implies that there is no significant diffusion, e.g. of lithium or oxygen vacancies.
6.3. Thermal expansion
The thermal expansion of petalite shows an orthorhombic pseudo-symmetry of the type α33 < 0 ≈ α11 < α22 (cf figures 9(j)–(l)). Components of tensors of different ranks cannot be compared directly, but as usually observed, the direction with maximum thermal expansion almost coincides with that of minimal longitudinal elastic stiffness and vice versa. Negative thermal expansion is observed along e3. In framework structures, negative thermal expansion is often due to a cooperative rotation of coordination polyhedra, and this is very likely the case in petalite as well. However, a confirmation of this hypothesis would require high temperature diffraction experiments. The thermal expansion provides no indication of a phase transition in the temperature range studied, but it is known that at temperatures T > 1200 K high temperature polymorphs are formed (Tagai et al 1982).
6.4. Thermodynamic properties
The significant discrepancy between the low temperature heat capacities obtained experimentally and those from model calculations were not to be expected as the theoretical and experimental elastic stiffness coefficients were in good agreement. The low frequency phonon density of states is usually dominated by the dispersion of the acoustic phonons, and once the slopes of the acoustic phonons, i.e. the elastic stiffness coefficients, are well described by a model, the low temperature heat capacity should be also predicted with a reasonable accuracy. A low frequency motion due to ions rattling in a coordination polyhedron slightly too large for them is unlikely, as all cation–oxygen bonds have values typical for tetrahedral coordination and the anisotropic displacement parameters of the cations are not excessively large at ambient temperatures (Effenberger 1980, Tagai et al 1982). However, petalite does have an unusual 180° Si–O–Si bond (Effenberger 1980). In analogy to the well-studied situation in β-cristobalite (Gambhir et al 1999), this points towards the possibility that, in fact, the time and space-averaged structure obtained from diffraction experiments may hide a small tilt of statically or dynamically disordered tetrahedra. This hypothesis is supported by the observation of rather anisotropic, plate-like atomic displacement parameters of those oxygen atoms, which participate in Si–O–Si bonds (Effenberger 1980). Low frequency contributions to the phonon density of states can be studied by thermal diffuse scattering (Bosak et al 2012) or by total scattering experiments (Dove et al 1997).
7. Conclusions
The current study represents a comprehensive characterization of physical properties of petalite. The data obtained in the current study complement and improve upon earlier data describing the thermodynamic and elastic behavior. Predictions concerning the electric field gradients can be tested experimentally and provide a benchmark for different models. The low temperature thermodynamic measurements, in conjunction with the model calculations, imply that it is likely that the description of petalite in terms of an averaged structure based on conventional diffraction experiments may be insufficient and that instead total scattering techniques with a pair distribution analysis and thermal diffuse scattering measurements may be required to fully understand the structure.
Acknowledgments
Financial support by the Deutsche Forschungsgemeinschaft (Project HA-5137/1) is gratefully acknowledged. The authors thank also Dr Heidi Höfer (University of Frankfurt) for performing the electron microprobe analyses.