Abstract
The role of the geometric phase effect on chemical reaction dynamics is explored by examining the hydrogen exchange process in the fundamental H+HD reaction. Results are presented for vibrationally excited HD molecules in the v = 4 vibrational level and for collision energies ranging from 1 μK to 100 K. It is found that, for collision energies below 3 K, inclusion of the geometric phase leads to dramatic enhancement or suppression of the reaction rates depending on the final quantum state of the HD molecule. The effect was found to be the most prominent for rotationally resolved integral and differential cross sections but it persists to a lesser extent in the vibrationally resolved and total reaction rate coefficients. However, no significant GP effect is present in the reactive channel leading to the D+H2 product or in the D+H2 HD+H reaction. A simple interference mechanism involving inelastic (nonreactive) and exchange scattering amplitudes is invoked to account for the observed GP effects. The computed results also reveal a shape resonance in the H+HD reaction near 1 K and the GP effect is found to influence the magnitude of the resonant part of the cross section. Experimental detection of the resonance may allow a sensitive probe of the GP effect in the H+HD reaction.
HD+H reaction. A simple interference mechanism involving inelastic (nonreactive) and exchange scattering amplitudes is invoked to account for the observed GP effects. The computed results also reveal a shape resonance in the H+HD reaction near 1 K and the GP effect is found to influence the magnitude of the resonant part of the cross section. Experimental detection of the resonance may allow a sensitive probe of the GP effect in the H+HD reaction.
Export citation and abstract BibTeX RIS
1. Introduction
The geometric phase (GP) effect in molecules arises from the sign change of Born–Oppenheimer (BO) adiabatic electronic wave functions (typically the ground state) when transported along a path encircling a conical intersection (CI). For the total Born–Oppenheimer wave function to remain single-valued, a corresponding sign-change must also occur on the nuclear motion wave function [1, 2]. This effect, referred to as the geometric phase or Berry's phase [3, 4], has long been a topic of numerous experimental and theoretical studies at higher temperatures. However, it has remained elusive in both experimental and theoretical results, due in part to cancellation of contributions from different angular momentum partial waves. The sign change applies even when the energy of nuclear-motion lies well below the energy of the CI and the nuclear-motion is confined to just one adiabatic electronic potential energy surface (PES). Mead and Truhlar [5, 6] generalized the BO method for systems with a CI including those with identical nuclei and showed that the sign change can be accounted for by introducing a vector potential or gauge potential in the Schrödinger equation for the nuclear-motion. The gauge potential approach is general and can be used to include electronic angular momentum coupling and derivative couplings with excited electronic states (which result in non-Abelian gauge potentials) [7–12].
There is a long history of experimental and theoretical investigations of the GP effect in chemical reaction dynamics. The H3 system has been the focus of the majority of the studies. It exhibits a CI between the ground and the first excited electronic states for equilateral triangle (i.e., 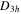 ) geometries [13]. The conical intersection occurs at an energy of about 2.7 eV. It has been shown that the GP alters the relative sign between the reactive and non-reactive scattering amplitudes for the H + H2 reaction which significantly modifies the angular dependence of the differential cross sections (DCSs) [14, 15]. Due to the indistinguishability of the three hydrogen atoms, the vast majority of experimental studies have focused on rotationally resolved DCSs in the H+D2 and D+H2 reactions or their reverse processes at energies close to the conical intersection [16–25]. However, no conclusive evidence of the GP effect has been demonstrated in these results when compared against quantum dynamics calculations performed with and without the GP. At these high collision energies, many values of the total angular momentum quantum number contribute to the reaction cross section and the GP effect, which may manifest in an angular momentum partial wave resolved DCS, vanishes when contributions from all angular momenta are included. This appears to be the case with all previously reported results on H+H2 and its isotopic counterparts at high collision energies [15, 22–24, 26–35]. Some relatively small rapidly varying oscillations in the DCS due to the GP have been seen in the theoretical DCSs at energies below that of the CI [31, 36, 37]. At energies above the CI, large GP effects on the DCS's were predicted which give rise to broader bi-modal features [36–38]. However, GP effects remained elusive in the integral cross sections or reaction rate coefficients at any energy, until recently [39–41]. A recent experimental attempt to measure the GP oscillations in the DCSs for the H + HD(
) geometries [13]. The conical intersection occurs at an energy of about 2.7 eV. It has been shown that the GP alters the relative sign between the reactive and non-reactive scattering amplitudes for the H + H2 reaction which significantly modifies the angular dependence of the differential cross sections (DCSs) [14, 15]. Due to the indistinguishability of the three hydrogen atoms, the vast majority of experimental studies have focused on rotationally resolved DCSs in the H+D2 and D+H2 reactions or their reverse processes at energies close to the conical intersection [16–25]. However, no conclusive evidence of the GP effect has been demonstrated in these results when compared against quantum dynamics calculations performed with and without the GP. At these high collision energies, many values of the total angular momentum quantum number contribute to the reaction cross section and the GP effect, which may manifest in an angular momentum partial wave resolved DCS, vanishes when contributions from all angular momenta are included. This appears to be the case with all previously reported results on H+H2 and its isotopic counterparts at high collision energies [15, 22–24, 26–35]. Some relatively small rapidly varying oscillations in the DCS due to the GP have been seen in the theoretical DCSs at energies below that of the CI [31, 36, 37]. At energies above the CI, large GP effects on the DCS's were predicted which give rise to broader bi-modal features [36–38]. However, GP effects remained elusive in the integral cross sections or reaction rate coefficients at any energy, until recently [39–41]. A recent experimental attempt to measure the GP oscillations in the DCSs for the H + HD(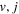 )
) 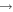 H + HD(
H + HD( ) reaction at energies below the CI was unsuccessful [22] where
) reaction at energies below the CI was unsuccessful [22] where  and
and  quantum numbers refer to the initial and final vibrational-rotational levels of the HD molecule. However, the GP effect has been shown to influence the bound state spectrum of triatomic molecules [6, 42–45] and experimental evidence of the GP effect have been reported in the vibrational spectrum of Cu3 [46–51], Li3 [52, 53], and Na3 [54].
quantum numbers refer to the initial and final vibrational-rotational levels of the HD molecule. However, the GP effect has been shown to influence the bound state spectrum of triatomic molecules [6, 42–45] and experimental evidence of the GP effect have been reported in the vibrational spectrum of Cu3 [46–51], Li3 [52, 53], and Na3 [54].
Despite the large number of experimental and theoretical studies of the H+H2 system and its isotopic counterparts, there are relatively few studies of the reaction involving initially vibrationally excited H2 or HD molecules. While Simbotin et al [55, 56] have carried out a careful analysis of the threshold behavior of quenching and reactive cross sections in D+H2 collisions for vibrational levels
collisions for vibrational levels  , the hydrogen exchange reactions in H+HD or D+HD collisions were not considered in their work. The GP effect was also not included in their study. When H2 or HD molecules are prepared in a vibrational level v = 4 or higher, the qualitative nature of the reaction dynamics changes. The vibrationally adiabatic potential energy curves of the H+H2 reaction exhibit potential wells for
, the hydrogen exchange reactions in H+HD or D+HD collisions were not considered in their work. The GP effect was also not included in their study. When H2 or HD molecules are prepared in a vibrational level v = 4 or higher, the qualitative nature of the reaction dynamics changes. The vibrationally adiabatic potential energy curves of the H+H2 reaction exhibit potential wells for  as opposed to a reaction barrier for
as opposed to a reaction barrier for 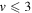 [24, 55–59]. Barrierless reactions may occur at appreciable rates even in the limit of zero collision energy [39–41, 60–64]. This limiting energy regime, referred to as cold or ultracold, has attracted considerable interest in recent years due to the proliferation in methods to cool and trap molecules and the possibility of quantum control of chemical reactions using external electric and magnetic fields [65–68]. At vanishingly small collision energies, only the s-wave (l = 0 angular momentum partial wave) contributes to the reaction rate and the partial wave summation collapses to just one term, the s-wave contribution. In our recent work [39–41], it was demonstrated that for the barrierless
[24, 55–59]. Barrierless reactions may occur at appreciable rates even in the limit of zero collision energy [39–41, 60–64]. This limiting energy regime, referred to as cold or ultracold, has attracted considerable interest in recent years due to the proliferation in methods to cool and trap molecules and the possibility of quantum control of chemical reactions using external electric and magnetic fields [65–68]. At vanishingly small collision energies, only the s-wave (l = 0 angular momentum partial wave) contributes to the reaction rate and the partial wave summation collapses to just one term, the s-wave contribution. In our recent work [39–41], it was demonstrated that for the barrierless 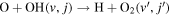 as well the H+H2
as well the H+H2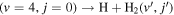 and H/D+HD(
and H/D+HD( H/D+HD(
H/D+HD( ) reactions, a large GP effect is present in the rotationally resolved integral and differential cross sections in the ultracold regime. The GP effect led to an enhancement or suppression of the reactivity depending on whether the scattering amplitudes for the direct and the looping/exchange paths that encircle the CI interfered constructively or destructively. In this paper, we present a detailed study of the GP effect in the H+HD(
) reactions, a large GP effect is present in the rotationally resolved integral and differential cross sections in the ultracold regime. The GP effect led to an enhancement or suppression of the reactivity depending on whether the scattering amplitudes for the direct and the looping/exchange paths that encircle the CI interfered constructively or destructively. In this paper, we present a detailed study of the GP effect in the H+HD( H+HD(
H+HD( ) reaction by analyzing final rotational state distributions, partial wave contributions to the cross sections, energy and angle resolved differential cross sections and total reaction rates. We will also explore the product D+H2 channel and examine why the GP effect does not influence the reaction rates in this case or its reverse reaction, D+H2
) reaction by analyzing final rotational state distributions, partial wave contributions to the cross sections, energy and angle resolved differential cross sections and total reaction rates. We will also explore the product D+H2 channel and examine why the GP effect does not influence the reaction rates in this case or its reverse reaction, D+H2 HD+H.
HD+H.
The paper is organized as follows: section 2 provides a brief description of the quantum dynamics approach and a simple model that illustrates how the GP effect manifests in ultracold barrierless chemical reactions. Results of the GP and NGP (no geometric phase) calculations for the H+HD ; D+H2 and D+H2
; D+H2 and D+H2 HD+H reactions are presented in section 3. This section also includes a discussion of resonant enhancement of the reaction due to a l = 1 shape resonance. Conclusions of our study are outlined in section 4.
HD+H reactions are presented in section 3. This section also includes a discussion of resonant enhancement of the reaction due to a l = 1 shape resonance. Conclusions of our study are outlined in section 4.
2. Method
2.1. Hyperspherical coordinates
The Schrödinger equation is solved using a numerically exact six-dimensional time-independent coupled-channel formalism implemented in the adiabatically adjusting principle axis hyperspherical (APH) coordinates [69–71]. This is enabled by partitioning the hyperradius into two regions: an inner region and an outer region. In the inner region, also called the interaction region (i.e., for small hyperradius ρ) where all three atoms are in close proximity, Smith–Whitten symmetrized hyperspherical or APH coordinates are used. In the outer region (i.e., for large hyperradius ρ) where the reactant and product channels become decoupled, a properly symmetrized set of Fock–Delves hyperspherical coordinates are used (one for each arrangement channel). The method accurately treats the body-frame Eckart singularities [70] associated with non-zero total angular momentum quantum number J and includes the geometric phase using the general vector potential approach [30, 72]. An adiabatic approach is used both in the inner and outer regions by discretizing the hyperradius ρ into a large number of sectors. The three-body Hamiltonian is diagonalized at the midpoint of each sector to obtain a set of 5D angular wave functions (hyperspherical surface functions). The 5D angular solutions are independent of the collision energy and need to be computed once for each value of J, inversion parity and identical particle exchange symmetry. They form the basis set for the coupled-channel equations in ρ and are used to compute a set of potential coupling matrices within each sector and the overlap matrices between adjacent sectors. The log-derivative propagator method of Johnson [73] is used to propagate the coupled equations from small to large ρ. Finally, the asymptotic boundary conditions are applied at large ρ to compute the scattering S matrix from which the cross sections and reaction rate coefficients are computed. The non-thermal reaction rate coefficients reported here are obtained by multiplying the reaction cross sections with the relative collision velocity.
2.2. How the GP effect manifests in the ultracold regime
Our previous work [39–41] illustrated that to observe the GP effect in reactive and inelastic scattering two criteria must be met: (i) the relevant adiabatic PES must display a CI, and (ii) the scattering amplitudes for the different pathways encircling the CI must have comparable magnitude and scatter into the same angular region. The latter criterion is partly satisfied in the ultracold regime where s-wave scattering dominates. In addition to the isotropic (i.e., s-wave) scattering, the ultracold regime can lead to an effective quantization of the scattering phase shift (i.e., the phase shift approaches an integral multiple of π) which often results in maximum constructive or destructive interference between the different scattering amplitudes. The details of the interference mechanism have been discussed in prior works [39–41] and only a brief description is given here.
There are two types of reactive pathways possible in H+HD collisions. One is a hydrogen exchange reaction, Ha+HbD( )
)  Hb+HaD(
Hb+HaD( ) where the two identical H atoms (labeled a and b for illustrative purpose) exchange with one another. This process should be considered together with a purely nonreactive inelastic transition Ha+HbD(
) where the two identical H atoms (labeled a and b for illustrative purpose) exchange with one another. This process should be considered together with a purely nonreactive inelastic transition Ha+HbD(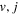 )
) 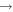 Ha+Hb(
Ha+Hb( )D where there is no H atom exchange. For an accurate description of H+HD scattering, both processes need to be taken into account as demonstrated in a recent experimental work of Jankunas et al [23]. The other process is a pure reactive collision, H+HD
)D where there is no H atom exchange. For an accurate description of H+HD scattering, both processes need to be taken into account as demonstrated in a recent experimental work of Jankunas et al [23]. The other process is a pure reactive collision, H+HD  D+H2. A detailed schematic diagram of the 2D slice of the ground state H3 electronic PES and the above two reaction pathways are given in figures 1(a) and (b) of [40]. To avoid repetition we do not reproduce the reaction pathways here but provide a brief description of each reaction mechanism. As our main focus is the hydrogen exchange reaction that shows the largest GP effect, the theoretical description is based on the exchange pathways depicted in figure 1(a) of [40] and prior works of Althorpe and collaborators [31–34]. If finel and fex are the scattering amplitudes for the 'inelastic' and 'exchange' pathways, they can be written in terms of the NGP and GP scattering amplitudes, fNGP and fGP, according to
D+H2. A detailed schematic diagram of the 2D slice of the ground state H3 electronic PES and the above two reaction pathways are given in figures 1(a) and (b) of [40]. To avoid repetition we do not reproduce the reaction pathways here but provide a brief description of each reaction mechanism. As our main focus is the hydrogen exchange reaction that shows the largest GP effect, the theoretical description is based on the exchange pathways depicted in figure 1(a) of [40] and prior works of Althorpe and collaborators [31–34]. If finel and fex are the scattering amplitudes for the 'inelastic' and 'exchange' pathways, they can be written in terms of the NGP and GP scattering amplitudes, fNGP and fGP, according to
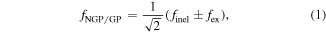
where the plus sign refers to NGP and the minus sign refers to GP. The square modulus of the scattering amplitudes for the NGP and GP calculations may be written as
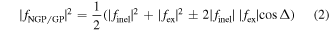
where the complex scattering amplitudes finel and fex are expressed as  and
and  and
and  is the phase difference between the exchange and inelastic pathways. The GP effect becomes significant when the two scattering amplitudes are of comparable magnitude, i.e.,
is the phase difference between the exchange and inelastic pathways. The GP effect becomes significant when the two scattering amplitudes are of comparable magnitude, i.e.,  which leads to
which leads to  . Further, if
. Further, if  then maximum (constructive) interference occurs for the NGP case and
then maximum (constructive) interference occurs for the NGP case and  and
and  . In contrast, if
. In contrast, if  then maximum (constructive) interference occurs for the GP case and
then maximum (constructive) interference occurs for the GP case and  and
and  . In the ultracold regime, an effective quantization of
. In the ultracold regime, an effective quantization of  can occur where n is an integer and the reaction can then be turned on or off depending simply on the sign of the interference term (since
can occur where n is an integer and the reaction can then be turned on or off depending simply on the sign of the interference term (since  ). On the other hand, if one of the scattering amplitudes is much greater than the other,
). On the other hand, if one of the scattering amplitudes is much greater than the other,  or
or  , then equation (2) becomes
, then equation (2) becomes  or
or  . In these cases, the interference term containing
. In these cases, the interference term containing  plays no role and the GP effect vanishes. When many partial waves contribute, as in higher energy collisions, the interference term averages out to zero (
plays no role and the GP effect vanishes. When many partial waves contribute, as in higher energy collisions, the interference term averages out to zero ( ) and there is no GP effect. The above theoretical description is also valid for the pure reactive case, H+HD
) and there is no GP effect. The above theoretical description is also valid for the pure reactive case, H+HD  D+H2 except the two scattering amplitudes for the different paths are replaced by
D+H2 except the two scattering amplitudes for the different paths are replaced by  and
and  . The phase quantization of
. The phase quantization of  can be understood in terms of scattering in a simple spherical square well potential for the different pathways (i.e., Levinson's theorem
can be understood in terms of scattering in a simple spherical square well potential for the different pathways (i.e., Levinson's theorem  and
and  but with a different number of bound states nex and ninel for the spherical well potentials traversed by the two pathways) [39]. As we demonstrate below, our explicit scattering calculations appear to validate this model, yielding
but with a different number of bound states nex and ninel for the spherical well potentials traversed by the two pathways) [39]. As we demonstrate below, our explicit scattering calculations appear to validate this model, yielding  values that are close to ±1 when the NGP or GP effect dominates.
values that are close to ±1 when the NGP or GP effect dominates.
3. Results and discussion
3.1. Basis set parameters and vibrationally adiabatic potentials
Extensive convergence tests have been carried out to determine appropriate values of the basis set truncation parameters for the surface function calculations in the APH angular coordinates θ and ϕ. The APH region was restricted to hyperradius  bohr with a logarithmic spacing in ρ. The parameters lmax and mmax control the number of basis functions in θ and ϕ in this region, respectively. For computational efficiency the hyperradial region in the APH coordinates is divided into five segments with increasingly larger basis functions as ρ increases. The basis set changes at ρ values 2.89, 3.61, 4.51, 5.63 and 7.03 bohr with (
bohr with a logarithmic spacing in ρ. The parameters lmax and mmax control the number of basis functions in θ and ϕ in this region, respectively. For computational efficiency the hyperradial region in the APH coordinates is divided into five segments with increasingly larger basis functions as ρ increases. The basis set changes at ρ values 2.89, 3.61, 4.51, 5.63 and 7.03 bohr with ( parameters (103, 190), (115, 214), (123, 232), (135, 250), and (143, 274), respectively. For J = 0 these basis sets led to surface function matrices of dimension 39 624, 49 764, 57 660, 68 136 and 79 056. A sequential diagonalization truncation (SDT) scheme is used to reduce the dimensionality of these matrices to 8916, 10 410, 11 817, 14 156 and 16 741, respectively. This leads to a significant savings in computational time, especially for
parameters (103, 190), (115, 214), (123, 232), (135, 250), and (143, 274), respectively. For J = 0 these basis sets led to surface function matrices of dimension 39 624, 49 764, 57 660, 68 136 and 79 056. A sequential diagonalization truncation (SDT) scheme is used to reduce the dimensionality of these matrices to 8916, 10 410, 11 817, 14 156 and 16 741, respectively. This leads to a significant savings in computational time, especially for  for which the surface function matrices are much larger. The J = 0 calculations included 300 coupled channel equations of which 81 are open channels and the rest are closed channels (asymptotically). Asymptotically these 300 channels correspond to different rovibrational levels of the HD and H2 molecules. In the outer region where Delves co-ordinates are used the coupled channel solutions are further propagated from
for which the surface function matrices are much larger. The J = 0 calculations included 300 coupled channel equations of which 81 are open channels and the rest are closed channels (asymptotically). Asymptotically these 300 channels correspond to different rovibrational levels of the HD and H2 molecules. In the outer region where Delves co-ordinates are used the coupled channel solutions are further propagated from  bohr to 50 bohr with a uniform spacing of
bohr to 50 bohr with a uniform spacing of  bohr. The number of basis functions in this region is controlled by an energy cutoff parameter which is taken to be 4.0 eV relative to the minimum energy of the asymptotic H2 diatomic potential. The global H3 PES reported by Boothroyd et al [74], referred to as the BKMP2 PES, was adopted for the calculations. The H3 PES of Mielke et al [75] yields comparable results for both the GP and NGP calculations as illustrated in our recent work [40]. Computations were performed for
bohr. The number of basis functions in this region is controlled by an energy cutoff parameter which is taken to be 4.0 eV relative to the minimum energy of the asymptotic H2 diatomic potential. The global H3 PES reported by Boothroyd et al [74], referred to as the BKMP2 PES, was adopted for the calculations. The H3 PES of Mielke et al [75] yields comparable results for both the GP and NGP calculations as illustrated in our recent work [40]. Computations were performed for 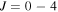 which yield converged cross sections for collision energies below 20 K. Nevertheless, results are presented for collision energies up to 100 K, which are converged with respect to basis set parameters but not the partial wave summation.
which yield converged cross sections for collision energies below 20 K. Nevertheless, results are presented for collision energies up to 100 K, which are converged with respect to basis set parameters but not the partial wave summation.
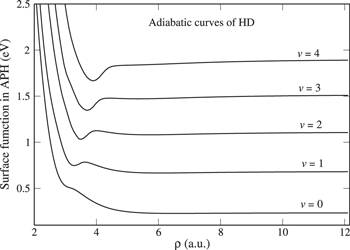
In figure 1 we present vibrationally adiabatic potentials for H+HD( ) collisions which depict a barrierless path for
) collisions which depict a barrierless path for  , consistent with previous analysis of Jankunas et al [24] The potentials for
, consistent with previous analysis of Jankunas et al [24] The potentials for  exhibit barriers in the incident or outgoing channels which suppress ultracold reactivity.
exhibit barriers in the incident or outgoing channels which suppress ultracold reactivity.
Figure 1. Vibrationally adiabatic potentials for the H+HD(v) collisions for vibrational levels  . The reaction becomes barrierless for vibrational levels 4 and higher.
. The reaction becomes barrierless for vibrational levels 4 and higher.
Download figure:
Standard image High-resolution image3.2. GP effect in H+HD( ) channels
) channels
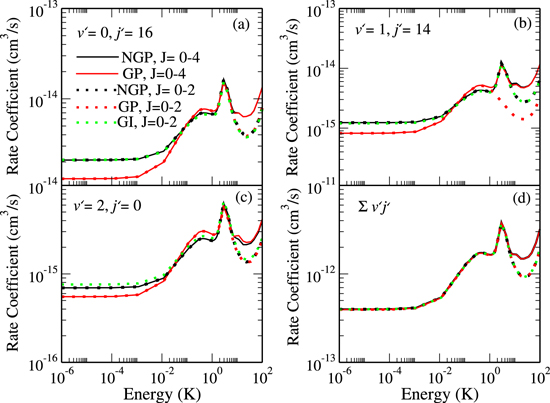
Figure 2 shows a few selected rotationally resolved reaction rate coefficients for the hydrogen exchange channel leading to H+HD( ); H+HD(
); H+HD( ); and H+HD(
); and H+HD( ) channels that show large GP effect. The results in the left panels correspond to even exchange symmetry and those in the right panels depict the odd exchange symmetry. The even and odd exchange symmetries refer to the symmetry of the nuclear motion wave function with respect to the permutation of the identical hydrogen nuclei. Since the hydrogen nuclei behave as spin 1/2 Fermions, the total molecular wave function (nuclear motion × electronic × nuclear spin) must be antisymmetric with respect to the permutation of the two identical H nuclei. Since the electronic wave function for H2 is a symmetric
) channels that show large GP effect. The results in the left panels correspond to even exchange symmetry and those in the right panels depict the odd exchange symmetry. The even and odd exchange symmetries refer to the symmetry of the nuclear motion wave function with respect to the permutation of the identical hydrogen nuclei. Since the hydrogen nuclei behave as spin 1/2 Fermions, the total molecular wave function (nuclear motion × electronic × nuclear spin) must be antisymmetric with respect to the permutation of the two identical H nuclei. Since the electronic wave function for H2 is a symmetric  state, the even (odd) nuclear motion wavefunction is multiplied by the odd (even) nuclear spin function with the appropriate statistical weight. These statistical weights are included in the rates plotted in figure 2 (1/4 for even and 3/4 for odd). The black and red curves denote NGP and GP rates, respectively. It is seen that the NGP rates dominate for the even exchange symmetry and the GP rates dominate for the odd exchange symmetry (however this is not always the case). For the
state, the even (odd) nuclear motion wavefunction is multiplied by the odd (even) nuclear spin function with the appropriate statistical weight. These statistical weights are included in the rates plotted in figure 2 (1/4 for even and 3/4 for odd). The black and red curves denote NGP and GP rates, respectively. It is seen that the NGP rates dominate for the even exchange symmetry and the GP rates dominate for the odd exchange symmetry (however this is not always the case). For the  results in panels (a) and (d), the GP and NGP results differ by more than two orders of magnitude. For the other transitions, they differ by 1-2 orders of magnitude. The peak in the reaction rates near 1 K is a shape resonance due to a
results in panels (a) and (d), the GP and NGP results differ by more than two orders of magnitude. For the other transitions, they differ by 1-2 orders of magnitude. The peak in the reaction rates near 1 K is a shape resonance due to a  partial wave which we will discuss in more detail in section 3.3.
partial wave which we will discuss in more detail in section 3.3.
Figure 2. Rotationally resolved reaction rate coefficients (cross section times the relative velocity) for H+HD( ); H+HD(
); H+HD( ); H+HD(
); H+HD( ) products in H+HD(
) products in H+HD( collisions as a function of the collision energy. Even and odd exchange symmetry results are presented in the left and right panels, respectively. In each panel, the red curves show the GP results and the black curves denote the NGP results. The results include all values of total angular momentum
collisions as a function of the collision energy. Even and odd exchange symmetry results are presented in the left and right panels, respectively. In each panel, the red curves show the GP results and the black curves denote the NGP results. The results include all values of total angular momentum  .
.
Download figure:
Standard image High-resolution imageFigure 3 shows the ratio of the square of the scattering amplitudes for the exchange (reactive) and inelastic (nonreactive) pathways (upper panels (a) and (c)) and average value of  for
for  and
and  (lower panels, (b) and (d)) for both even and odd exchange symmetries as functions of the collision energy. Results for J = 0, J = 1 and that summed over
(lower panels, (b) and (d)) for both even and odd exchange symmetries as functions of the collision energy. Results for J = 0, J = 1 and that summed over  are shown in black, red and blue curves, respectively, for the H+HD(
are shown in black, red and blue curves, respectively, for the H+HD( ) product channel. It is seen that
) product channel. It is seen that  values for the summed
values for the summed  case approach ±1 (+1 in panel (b) and -1 in panel (d)) for collision energies below 1 mK where only the
case approach ±1 (+1 in panel (b) and -1 in panel (d)) for collision energies below 1 mK where only the  partial wave contributes. The GP effect is most pronounced in this regime where the exchange (reactive) and inelastic (nonreactive) scattering amplitudes have comparable magnitude (i.e., their ratio is near unity). Hence, the square modulus of the total scattering amplitude for the NGP and GP cases can be approximated as
partial wave contributes. The GP effect is most pronounced in this regime where the exchange (reactive) and inelastic (nonreactive) scattering amplitudes have comparable magnitude (i.e., their ratio is near unity). Hence, the square modulus of the total scattering amplitude for the NGP and GP cases can be approximated as  (when NGP dominates) and
(when NGP dominates) and  (when GP dominates) in the ultracold regime. This explains the dominance of the NGP and GP rates at low energies in panels (a) and (d) of figure 2. As the collision energy increases contributions from J = 1 (
(when GP dominates) in the ultracold regime. This explains the dominance of the NGP and GP rates at low energies in panels (a) and (d) of figure 2. As the collision energy increases contributions from J = 1 ( partial wave) becomes important. However, in panels (b) and (d) of figure 3 it is seen that the sign of
partial wave) becomes important. However, in panels (b) and (d) of figure 3 it is seen that the sign of  is flipped for J = 1 leading to
is flipped for J = 1 leading to  (as
(as  = −1 in panel (b)) and
= −1 in panel (b)) and  (as
(as  = +1 in panel (d)) for J = 1. This also explains why the NGP contribution is suppressed and the GP contribution is enhanced at the resonance region near 1 K in figure 2(a). The opposite effect is seen in figure 2(d). A similar trend is observed for
= +1 in panel (d)) for J = 1. This also explains why the NGP contribution is suppressed and the GP contribution is enhanced at the resonance region near 1 K in figure 2(a). The opposite effect is seen in figure 2(d). A similar trend is observed for  and
and  values for the final states presented in panels (b), (c), (e) and (f) of figure (2). At higher energies,
values for the final states presented in panels (b), (c), (e) and (f) of figure (2). At higher energies,  tends to oscillate about zero which leads to a small interference term and negligible GP effect. This is illustrated further in figure 4 which shows a
tends to oscillate about zero which leads to a small interference term and negligible GP effect. This is illustrated further in figure 4 which shows a  vs
vs  plot for all of the open rotationally resolved H+HD(
plot for all of the open rotationally resolved H+HD( ) channels at a collision energy of 1μK. The even and odd exchange symmetry cases are plotted in black and red dots, respectively. It is seen that the majority of
) channels at a collision energy of 1μK. The even and odd exchange symmetry cases are plotted in black and red dots, respectively. It is seen that the majority of  values are clustered near ±1 (+1 for even and −1 for odd exchange symmetry) indicating that the phase difference
values are clustered near ±1 (+1 for even and −1 for odd exchange symmetry) indicating that the phase difference  is essentially quantized at low energies leading to significant GP effects in most rotationally resolved rate coefficients.
is essentially quantized at low energies leading to significant GP effects in most rotationally resolved rate coefficients.
Figure 3. Ratio of the square of the scattering amplitudes for the exchange (reactive) and inelastic (non-reactive) pathways (upper panels) and average value of  (lower panels) for both even (left panels) and odd (right panels) exchange symmetries as functions of the collision energy. Results are presented for the H+HD(
(lower panels) for both even (left panels) and odd (right panels) exchange symmetries as functions of the collision energy. Results are presented for the H+HD( ) product channel.
) product channel.
Download figure:
Standard image High-resolution imageFigure 4. Plot of 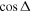 versus
versus  for all of the rotationally resolved H+HD(
for all of the rotationally resolved H+HD( ) channels in H+HD(
) channels in H+HD(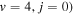 collisions. The final states with
collisions. The final states with 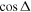 values clustered around ±1 show markedly higher GP effect.
values clustered around ±1 show markedly higher GP effect.
Download figure:
Standard image High-resolution imageIn figure 5 we present the gauge invariance check of our GP results. The vector potential approach for including the GP is based on a general vector potential of the form  where η is the azimuthal angle which encircles the CI and m is an integer [5]. Even
where η is the azimuthal angle which encircles the CI and m is an integer [5]. Even  correspond to NGP and odd
correspond to NGP and odd  correspond to GP. Our NGP and GP calculations use m = 0 and 1, respectively. The gauge invariance check (green dots) shown in figure 5 uses m = 2, which is equivalent to a NGP calculation. Figure 5 shows that gauge invariance is well satisfied for the same final states depicted in figure 2 but restricted to total
correspond to GP. Our NGP and GP calculations use m = 0 and 1, respectively. The gauge invariance check (green dots) shown in figure 5 uses m = 2, which is equivalent to a NGP calculation. Figure 5 shows that gauge invariance is well satisfied for the same final states depicted in figure 2 but restricted to total  (to reduce the computational time). This confirms that the results are well converged and the large GP effects are genuine.
(to reduce the computational time). This confirms that the results are well converged and the large GP effects are genuine.
Figure 5. Gauge invariance of the GP rate coefficients shown in figure 2. To reduce computational time, only total angular momentum  were included in the gauge invariance calculations. The gauge invariance test shown by the dotted green curve reproduces the NGP results as expected.
were included in the gauge invariance calculations. The gauge invariance test shown by the dotted green curve reproduces the NGP results as expected.
Download figure:
Standard image High-resolution imageFigure 6 shows vibrationally resolved rate coefficients for 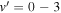 for the GP (shown in red) and NGP (shown in black) cases summed over all open rotational levels. To avoid cluttering,
for the GP (shown in red) and NGP (shown in black) cases summed over all open rotational levels. To avoid cluttering,  results are plotted in the upper panels ((a) and (c)) and
results are plotted in the upper panels ((a) and (c)) and  product states are plotted in the lower panels ((b) and (d)). Panels (a) and (b) are for even exchange symmetry and panels (c) and (d) are for odd exchange symmetry. Results for
product states are plotted in the lower panels ((b) and (d)). Panels (a) and (b) are for even exchange symmetry and panels (c) and (d) are for odd exchange symmetry. Results for  and 2 are denoted by solid curves while
and 2 are denoted by solid curves while 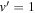 and 3 are denoted by dashed curves. It is seen that the GP effect persists in vibrationally resolved rate coefficients though to a lesser extent compared to the rotationally resolved rates. The GP and NGP rates differ by nearly an order of magnitude for
and 3 are denoted by dashed curves. It is seen that the GP effect persists in vibrationally resolved rate coefficients though to a lesser extent compared to the rotationally resolved rates. The GP and NGP rates differ by nearly an order of magnitude for  and 1 for both symmetries. It is striking to note that after summing over all open rotational states, the NGP rates exceed the GP rates for even exchange symmetry while the GP rates exceed the NGP rates for the odd exchange symmetry.
and 1 for both symmetries. It is striking to note that after summing over all open rotational states, the NGP rates exceed the GP rates for even exchange symmetry while the GP rates exceed the NGP rates for the odd exchange symmetry.
Figure 6. Vibrationally resolved rate coefficients for 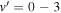 as a function of the collision energy. Left panels: even exchange symmetry; right panels: odd exchange symmetry. All values of total angular momentum J = 0 – 4 are included.
as a function of the collision energy. Left panels: even exchange symmetry; right panels: odd exchange symmetry. All values of total angular momentum J = 0 – 4 are included.
Download figure:
Standard image High-resolution imageThe total and J-resolved rate coefficients summed over 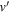 and
and  are shown in figure 7 (left panels) for even (panel a) and odd (panel b) exchange symmetries as a function of the collision energy. The same but summed over even and odd exchange symmetries is shown in the right panel of figure 7 (panel (c)). Note that appropriate nuclear spin statistics factors have been included in the even and odd exchange symmetry contributions and the sum reflects this. The GP and NGP results are shown in red and black curves, respectively. The thick solid curves include contributions from
are shown in figure 7 (left panels) for even (panel a) and odd (panel b) exchange symmetries as a function of the collision energy. The same but summed over even and odd exchange symmetries is shown in the right panel of figure 7 (panel (c)). Note that appropriate nuclear spin statistics factors have been included in the even and odd exchange symmetry contributions and the sum reflects this. The GP and NGP results are shown in red and black curves, respectively. The thick solid curves include contributions from  whereas the thin solid, dashed, dashed dotted, thick dotted and dotted dashed curves correspond to
whereas the thin solid, dashed, dashed dotted, thick dotted and dotted dashed curves correspond to  and 4, respectively. As the angular momentum barrier in the entrance channel increases with J, the contribution of higher partial waves to the reaction rate coefficients decreases as the collision energy is reduced. The pure s-wave limit is reached for collision energies below 10 mK. It is seen that the rate coefficients are converged with respect to angular momentum partial wave sum for energies up to 20 K. The GP effect persists for collision energies up to about 0.1 K and also slightly in the resonant part of the cross section near 1.0 K. Clearly, experimental verification of the resonance can be a sensitive probe of the GP effect in the H+HD(
and 4, respectively. As the angular momentum barrier in the entrance channel increases with J, the contribution of higher partial waves to the reaction rate coefficients decreases as the collision energy is reduced. The pure s-wave limit is reached for collision energies below 10 mK. It is seen that the rate coefficients are converged with respect to angular momentum partial wave sum for energies up to 20 K. The GP effect persists for collision energies up to about 0.1 K and also slightly in the resonant part of the cross section near 1.0 K. Clearly, experimental verification of the resonance can be a sensitive probe of the GP effect in the H+HD( reaction. In the ultracold regime (below 1 mK), the NGP rate coefficient for the even exchange symmetry (panel (a)) summed over
reaction. In the ultracold regime (below 1 mK), the NGP rate coefficient for the even exchange symmetry (panel (a)) summed over  exceeds the GP rates by a factor of 3. This is reversed for odd exchange symmetry for which the GP rates exceed the NGP rates by a similar factor (panel (b)). Due to the higher statistical weight for the odd exchange symmetry contribution, the ultracold GP (the thick solid red curve) rate in panel (c) is about 1.7 times larger than the NGP (the thick solid black curve) rate. In all three panels, the J-resolved GP and NGP rates (especially for J = 0 and 1) alternate between each other. Consequently, the dominance of the GP/NGP rates is reversed in the resonance region compared to the ultracold region. Its origin can clearly be traced to the enhancement of the J = 1 rates due to the
exceeds the GP rates by a factor of 3. This is reversed for odd exchange symmetry for which the GP rates exceed the NGP rates by a similar factor (panel (b)). Due to the higher statistical weight for the odd exchange symmetry contribution, the ultracold GP (the thick solid red curve) rate in panel (c) is about 1.7 times larger than the NGP (the thick solid black curve) rate. In all three panels, the J-resolved GP and NGP rates (especially for J = 0 and 1) alternate between each other. Consequently, the dominance of the GP/NGP rates is reversed in the resonance region compared to the ultracold region. Its origin can clearly be traced to the enhancement of the J = 1 rates due to the  shape resonance.
shape resonance.
Figure 7. Total angular momentum resolved (partial wave resolved since l = J for j = 0) rate coefficients for the H+HD( H+HD reaction summed over all energetically accessible rotational and vibrational levels of the product HD molecule. The left panel (a) is for even exchange symmetry and (b) is for the odd exchange symmetry. Panel (c) on the right presents total rate coefficients summed over even and odd exchange symmetries. Appropriate nuclear spin statistics factors have been included in all of the rate coefficients.
H+HD reaction summed over all energetically accessible rotational and vibrational levels of the product HD molecule. The left panel (a) is for even exchange symmetry and (b) is for the odd exchange symmetry. Panel (c) on the right presents total rate coefficients summed over even and odd exchange symmetries. Appropriate nuclear spin statistics factors have been included in all of the rate coefficients.
Download figure:
Standard image High-resolution image3.3. Resonances in H+HD reaction
Both the hydrogen exchange channel and the D+H2 product channel (described in section 3.5) show a resonance feature in the energy dependent reaction rate coefficient at about 1.0 K. The resonance feature occurs in the rotationally and vibrationally resolved rate coefficients as well as the total rate coefficient. It also occurs in both the GP and NGP results. The partial wave resolved rate coefficients shown in figure 7 indicate that the resonance is due to an  partial wave (J = 1, for initial j = 0). This is further confirmed by the argand diagrams shown in figure 8 for the
partial wave (J = 1, for initial j = 0). This is further confirmed by the argand diagrams shown in figure 8 for the  final state for J = 0 (panels (a) and (c)) and J = 1 (panels (b) and (d)). The left and right panels display results for the even and odd exchange symmetries, respectively. For the even exchange symmetry, as panel (a) of figure 7 shows, the GP rates for J = 1 exceed the NGP rates near 1 K. This is reversed for the odd exchange symmetry for which the NGP rates for J = 1 exceed the GP rates (panel (b) of figure 7). The red data points correspond to the energies in the resonance region. Only the J = 1 results shown in the lower panels for both symmetries display a looping behavior characteristic of a scattering resonance. This looping behavior is a consequence of the
final state for J = 0 (panels (a) and (c)) and J = 1 (panels (b) and (d)). The left and right panels display results for the even and odd exchange symmetries, respectively. For the even exchange symmetry, as panel (a) of figure 7 shows, the GP rates for J = 1 exceed the NGP rates near 1 K. This is reversed for the odd exchange symmetry for which the NGP rates for J = 1 exceed the GP rates (panel (b) of figure 7). The red data points correspond to the energies in the resonance region. Only the J = 1 results shown in the lower panels for both symmetries display a looping behavior characteristic of a scattering resonance. This looping behavior is a consequence of the  phase shift associated with a resonance. A Lorentzian least-squares fit of the J = 1 GP resonance gives a resonance energy of 0.82 K and a width of
phase shift associated with a resonance. A Lorentzian least-squares fit of the J = 1 GP resonance gives a resonance energy of 0.82 K and a width of 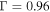 K (or lifetime
K (or lifetime 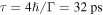 ). We believe this is the first time a reactive scattering resonance has been observed in the H+HD reaction at a collision energy near 1 K.
). We believe this is the first time a reactive scattering resonance has been observed in the H+HD reaction at a collision energy near 1 K.
Figure 8. Argand diagram for H+HD( H+HD(
H+HD(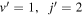 ) collisions for J = 0 and 1. Left panel: even exchange symmetry; right panel: odd exchange symmetry. The J = 0 results show no resonances feature while the J = 1 results indicate looping features characteristic of a resonance. Energies in the resonance region are denoted by red data points for both GP and NGP cases.
) collisions for J = 0 and 1. Left panel: even exchange symmetry; right panel: odd exchange symmetry. The J = 0 results show no resonances feature while the J = 1 results indicate looping features characteristic of a resonance. Energies in the resonance region are denoted by red data points for both GP and NGP cases.
Download figure:
Standard image High-resolution image3.4. Differential cross sections
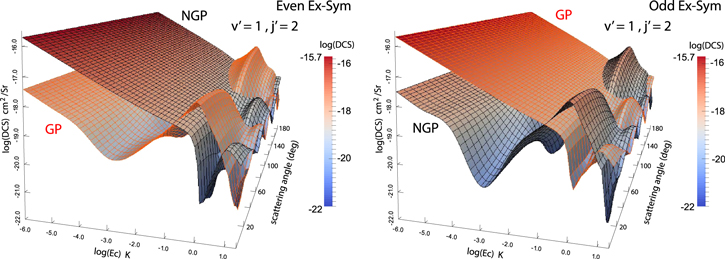
The results presented thus far have focused on reaction rate coefficients obtained by multiplying the integral cross sections with the relative collision velocity. In this section we discuss the differential cross section (DCS) for the hydrogen exchange channel. Figure 9 displays three-dimensional plots of differential cross sections as a function of both energy and scattering angle for the H+HD 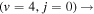 H+HD
H+HD  reaction. The DCSs are plotted for both even (left panel) and odd (right panel) exchange symmetries. The reaction rate for this final state has already been presented in panels (b) and (e) of figure 2. At low energies, the NGP rate dominates over the GP rate for the even exchange symmetry whereas the trend is reversed for the odd exchange symmetry. The NGP and GP results show the isotropic distribution in scattering angle and Wigner threshold behavior [76, 77] in scattering energy below 10 mK. The enhancement or suppression of the NGP or GP DCS in the ultracold regime is a direct outcome of the constructive or destructive interference between the inelastic (non-reactive) and exchange (reactive) scattering amplitudes which is maximized in the s-wave limit. As higher partial waves begin to contribute the effect becomes less pronounced, except when a scattering resonance is present. For example, while the NGP DCS dominates over its GP counterpart in the s-wave regime for the even exchange symmetry (left panel), the GP DCS exceeds the NGP values for collision energies above 100 mK. This is due to the
reaction. The DCSs are plotted for both even (left panel) and odd (right panel) exchange symmetries. The reaction rate for this final state has already been presented in panels (b) and (e) of figure 2. At low energies, the NGP rate dominates over the GP rate for the even exchange symmetry whereas the trend is reversed for the odd exchange symmetry. The NGP and GP results show the isotropic distribution in scattering angle and Wigner threshold behavior [76, 77] in scattering energy below 10 mK. The enhancement or suppression of the NGP or GP DCS in the ultracold regime is a direct outcome of the constructive or destructive interference between the inelastic (non-reactive) and exchange (reactive) scattering amplitudes which is maximized in the s-wave limit. As higher partial waves begin to contribute the effect becomes less pronounced, except when a scattering resonance is present. For example, while the NGP DCS dominates over its GP counterpart in the s-wave regime for the even exchange symmetry (left panel), the GP DCS exceeds the NGP values for collision energies above 100 mK. This is due to the  = 1 shape resonance that enhances the GP DCS for energies above 100 mK (see also the J-resolved rate coefficients in figure 7 and the Argand plot in figure 8). The same scenario occurs for the odd exchange symmetry (right panel) for which the GP DCS dominates over the NGP results in the ultracold regime but not in the resonance region. In this case, the shape resonance enhances the NGP contribution.
= 1 shape resonance that enhances the GP DCS for energies above 100 mK (see also the J-resolved rate coefficients in figure 7 and the Argand plot in figure 8). The same scenario occurs for the odd exchange symmetry (right panel) for which the GP DCS dominates over the NGP results in the ultracold regime but not in the resonance region. In this case, the shape resonance enhances the NGP contribution.
Figure 9. Differential cross sections for H+HD  H+HD
H+HD  reaction as a function of the scattering angle and the collision energy. The left and right panels show results for even and odd exchange symmetries. The results include contributions from
reaction as a function of the scattering angle and the collision energy. The left and right panels show results for even and odd exchange symmetries. The results include contributions from  .
.
Download figure:
Standard image High-resolution imageIn figure 10, a two dimensional slice of the differential cross section is presented as a function of the scattering angle for the same final state as in figure 9 for collision energies of 0.812 K (near the shape resonance) and 8.0 K. Only results for the odd exchange symmetry are presented. It is seen that while the scattering angle dependence of the NGP DCS is nearly the same at both energies that of the GP DCS is very different. At the resonance energy (top panel) the NGP DCS exceeds the GP result by an order of magnitude except in the narrow range of scattering angle between 80°–120° where the NGP result dips below its GP counterpart. As a result, the integral cross sections and reaction rates show higher values for the NGP case in the resonance region. However, at 8.0 K where there is no resonance, contributions from partial waves 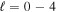 are required for convergence and the s-wave contribution is not dominant anymore. Also, in this case, the DCS for both GP and NGP is symmetric at about
are required for convergence and the s-wave contribution is not dominant anymore. Also, in this case, the DCS for both GP and NGP is symmetric at about  and out of phase in scattering angle between 50°–140°. This leads to no observable difference between GP and NGP cross sections when integrated over the scattering angle as seen in the reaction rate depicted in figure 2. A similar behavior is found for the even exchange symmetry case.
and out of phase in scattering angle between 50°–140°. This leads to no observable difference between GP and NGP cross sections when integrated over the scattering angle as seen in the reaction rate depicted in figure 2. A similar behavior is found for the even exchange symmetry case.
Figure 10. Differential cross section for H+HD  H+HD
H+HD  reaction as a function of the scattering angle at two different collision energies of 0.812 K (panel (a), near the shape resonance) and 8.0 K (panel (b)) for the odd exchange symmetry. The contributions from
reaction as a function of the scattering angle at two different collision energies of 0.812 K (panel (a), near the shape resonance) and 8.0 K (panel (b)) for the odd exchange symmetry. The contributions from  are included.
are included.
Download figure:
Standard image High-resolution imageBesides the rate coefficients shown in figure 2 there are many other rotationally resolved final states that show large GP/NGP effects. These are listed in table 1 along with the two scattering amplitudes, average value of 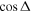 and the ratio
and the ratio  at 1μK. Only state-to-state rate coefficients that are greater than
at 1μK. Only state-to-state rate coefficients that are greater than  cm3 s−1 are shown. A significant GP effect is found in most of the rotationally resolved rate coefficients for both exchange symmetries. The most prominent are
cm3 s−1 are shown. A significant GP effect is found in most of the rotationally resolved rate coefficients for both exchange symmetries. The most prominent are  for which NGP or GP rates differ by more than two orders of magnitude. For these states, both the ratio
for which NGP or GP rates differ by more than two orders of magnitude. For these states, both the ratio  and
and  values approach 1 for J = 0. The sign of
values approach 1 for J = 0. The sign of  alternates for even (+1) and odd (−1) exchange symmetries (but this is not always the case). For even exchange symmetry, the square moduli of total NGP and GP scattering amplitudes are given by
alternates for even (+1) and odd (−1) exchange symmetries (but this is not always the case). For even exchange symmetry, the square moduli of total NGP and GP scattering amplitudes are given by  and
and  as
as  . Hence the NGP rates remain larger than the GP rates for this case. This trend is reversed for the odd exchange symmetry for which
. Hence the NGP rates remain larger than the GP rates for this case. This trend is reversed for the odd exchange symmetry for which  and
and  (
( ). This appears to be the case for the majority of rotational resolved rate coefficients for the hydrogen exchange reactions in H+HD collisions. For other
). This appears to be the case for the majority of rotational resolved rate coefficients for the hydrogen exchange reactions in H+HD collisions. For other 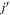 states where moderate GP effects are present such as
states where moderate GP effects are present such as  and 3 the ratio
and 3 the ratio 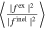 deviates from unity which suppresses the interference term although
deviates from unity which suppresses the interference term although 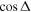 is close to 1.
is close to 1.
Table 1.
Ultracold ( ) rate coefficients for the H+HD(
) rate coefficients for the H+HD( HD+H; D+H2 reaction with and without geometric phase effects, the ratio of the average square modulus of the scattering amplitudes between the different pathways for two reactions,
HD+H; D+H2 reaction with and without geometric phase effects, the ratio of the average square modulus of the scattering amplitudes between the different pathways for two reactions,  , and the ratio of the GP and NGP rates are listed. The even and odd denote the exchange symmetry for H+HD(
, and the ratio of the GP and NGP rates are listed. The even and odd denote the exchange symmetry for H+HD( HD+H reaction. The data include the appropriate nuclear spin statistical weights.
HD+H reaction. The data include the appropriate nuclear spin statistical weights.
H+HD( ) ) |

|
HD+H reaction | ||||
|---|---|---|---|---|---|---|

|

|
NGP rate (cm3/s) | GP rate (cm3/s) |
|
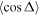
|

|
| 0 | 0(evn) |

|

|
1.30 | 0.99 |

|
| 0 | 0(odd) |

|

|
1.36 | −0.99 | 157 |
| 0 | 1(evn) |

|

|
1.31 | 0.99 |

|
| 0 | 1(odd) |

|

|
1.48 | −0.99 | 110 |
| 0 | 4(evn) |

|

|
1.24 | 0.98 |

|
| 0 | 4(odd) |

|

|
1.23 | −0.99 | 226 |
| 1 | 0(evn) |

|

|
0.69 | 0.95 |
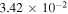
|
| 1 | 0(odd) |

|

|
0.79 | −0.88 | 15 |
| 1 | 2(evn ) |

|

|
0.77 | 0.97 |

|
| 1 | 2(odd) |

|

|
1.02 | −0.96 | 62 |
| 1 | 4(evn) |

|

|
0.50 | 0.92 |
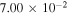
|
| 1 | 4(odd) |

|
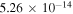
|
0.58 | −0.91 | 15 |
| 2 | 1(evn) |

|

|
0.82 | 0.72 | 0.16 |
| 2 | 1(odd) |

|
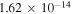
|
1.51 | −0.88 | 13 |
| 2 | 4(evn) |

|
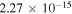
|
0.35 | 0.84 | 0.15 |
| 2 | 4(odd) |

|

|
0.33 | −0.84 | 6.23 |
| 2 | 6(evn) |
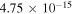
|

|
0.28 | 0.94 | 0.12 |
| 2 | 6(odd) |
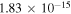
|

|
0.27 | −0.96 | 8.54 |
| 3 | 4(evn) |

|

|
0.30 | 0.95 | 0.11 |
| 3 | 4(odd) | 6.40 
|

|
0.21 | −0.97 | 6.73 |
H+HD(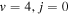 ) ) |

|
D+H2 reaction | ||||
|

|
NGP rate (cm3/s) | GP rate (cm3/s) |

|

|
|
| 0 | 6 |
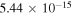
|
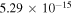
|
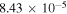
|
0.76 | 0.97 |
| 0 | 8 |
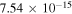
|

|

|
−0.62 | 1.03 |
| 0 | 9 |
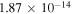
|

|

|
0.89 | 0.96 |
| 0 | 10 |

|

|
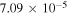
|
0.38 | 0.99 |
| 1 | 7 |

|
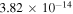
|

|
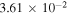
|
0.99 |
| 1 | 8 |

|

|

|
−0.99 | 1.09 |
| 2 | 3 |

|

|
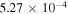
|
−0.26 | 1.02 |
| 2 | 4 |

|
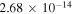
|

|
−0.49 | 1.04 |
| 3 | 0 |

|

|

|
−0.85 | 1.02 |
| 3 | 1 |
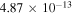
|

|

|
0.98 | 0.98 |
| 3 | 3 |

|

|

|
−0.34 | 1.00 |
We believe the results presented here for the H+HD exchange reaction shed new insights on when the GP effect may manifest in chemical reactions. For the GP effect to manifest, the interference term in equation (2) must have comparable magnitude as the pure inelastic and exchange terms and must survive the partial wave summation. In the ultracold limit where s-wave scattering dominates, the partial wave summation collapses to just one term presenting an ideal scenario for maximum constructive and destructive interference. At higher energies, out of phase contributions from different partial waves cancel the interference term. Our findings are consistent with previous studies of the H+D2 reaction by Kendrick [27]. Our results also explain why the interference term was not observable in the recent experimental studies of the H+HD reaction by Jankunas et al [22, 23].
3.5. D+H2 product channel
Our discussion of the GP effect has so far been centered around the hydrogen exchange channel in H+HD collisions. Here we examine the reactive channel leading to the D+H2 product. Figure 11 shows GP and NGP rate coefficients for rotationally resolved (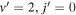 ),
), 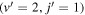 ,
,  ),
),  , and total rate coefficients summed over all open
, and total rate coefficients summed over all open  and
and  levels of H2. Panels (a), (b), (d) and (e) display rotationally resolved reaction rates whereas panels (c) and (f) present total reaction rates. For the pure reactive case the H2 molecule is formed in even or odd rotational states which corresponds to odd or even nuclear spin states. Results for even rotational levels (even exchange symmetry) are shown in the left panels and for odd rotational levels (odd exchange symmetry) are shown in the right panels. The rate coefficients include appropriate nuclear spin statistics factors of 1/4 for the even rotational levels (para-H2) and 3/4 for the odd rotational levels (orth-H2). It is seen that the GP and NGP rate coefficients are nearly indistinguishable for all cases, consistent with previous findings at higher energies. This is due to the dominance of the direct pathway as illustrated in figure 12 for
levels of H2. Panels (a), (b), (d) and (e) display rotationally resolved reaction rates whereas panels (c) and (f) present total reaction rates. For the pure reactive case the H2 molecule is formed in even or odd rotational states which corresponds to odd or even nuclear spin states. Results for even rotational levels (even exchange symmetry) are shown in the left panels and for odd rotational levels (odd exchange symmetry) are shown in the right panels. The rate coefficients include appropriate nuclear spin statistics factors of 1/4 for the even rotational levels (para-H2) and 3/4 for the odd rotational levels (orth-H2). It is seen that the GP and NGP rate coefficients are nearly indistinguishable for all cases, consistent with previous findings at higher energies. This is due to the dominance of the direct pathway as illustrated in figure 12 for  (panel (a)) and
(panel (a)) and  (panel (c)) where
(panel (c)) where  is plotted as a function of the collision energy. The black, red, and blue curves denote contributions from
is plotted as a function of the collision energy. The black, red, and blue curves denote contributions from  and
and 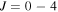 , respectively. In each case, the ratio is
, respectively. In each case, the ratio is 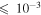 for energies ranging from 1 μK to 100 K which implies
for energies ranging from 1 μK to 100 K which implies 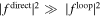 . Thus, negligible interference occurs between the direct and looping pathways. The corresponding average values of
. Thus, negligible interference occurs between the direct and looping pathways. The corresponding average values of  are plotted in panels (b) and (d) (for
are plotted in panels (b) and (d) (for 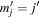 ). Although
). Although  values for the
values for the  state (panel (b)) lie close to 1 (especially for J = 1) the very small value of the looping scattering amplitude makes the interference term vanish leading to no observable GP effect. For the
state (panel (b)) lie close to 1 (especially for J = 1) the very small value of the looping scattering amplitude makes the interference term vanish leading to no observable GP effect. For the  product state (panel (d)), the
product state (panel (d)), the  values are close to zero and the GP effect is even further suppressed. The bottom part of table 1 lists reactive rate coefficients for some selected H2 ro-vibrational levels at a collision energy of 1 μK. No GP effect is present for these or any other rovibrational levels of the H2 product. The ratio of the scattering amplitudes,
values are close to zero and the GP effect is even further suppressed. The bottom part of table 1 lists reactive rate coefficients for some selected H2 ro-vibrational levels at a collision energy of 1 μK. No GP effect is present for these or any other rovibrational levels of the H2 product. The ratio of the scattering amplitudes,  remains
remains  10−4 for all final states making the interference term vanish, although for some cases
10−4 for all final states making the interference term vanish, although for some cases  is close to 1.
is close to 1.
Figure 11. Rotationally resolved and total rate coefficients for the H+HD( D+H2 reaction as a function of the incident collision energy. Left panel: even rotational states; right panel: odd rotational states. Note that there is no observable GP effect in this case. All values of total angular momentum J = 0 – 4 are included.
D+H2 reaction as a function of the incident collision energy. Left panel: even rotational states; right panel: odd rotational states. Note that there is no observable GP effect in this case. All values of total angular momentum J = 0 – 4 are included.
Download figure:
Standard image High-resolution imageFigure 12. Ratio of the square of the scattering amplitude for the direct and looping pathways (upper panels) and average value of  (lower panels) for both even (left panels) and odd (right panels) rotational states as functions of the collision energy. Results are presented for the H+HD(
(lower panels) for both even (left panels) and odd (right panels) rotational states as functions of the collision energy. Results are presented for the H+HD( D+H2
D+H2 ) reactions.
) reactions.
Download figure:
Standard image High-resolution image3.6. Reverse reaction: D+H2 H+HD
H+HD
The results presented so far indicated no observable GP effect in the D+H2 product channel compared to the strong GP effect in the H+HD channel. It would be interesting to examine whether the reverse reaction, D+H2 H+HD, would exhibit any noticeable GP effect. Figure 13 displays the rotationally resolved and total rate coefficients for the D+H2
H+HD, would exhibit any noticeable GP effect. Figure 13 displays the rotationally resolved and total rate coefficients for the D+H2 H+HD reaction for total angular momentum summed over
H+HD reaction for total angular momentum summed over  (solid curves). Like the previous cases, the NGP and GP results are denoted by black and red curves, respectively. The panels (a), (b) and (c) show the rotationally resolved rate coefficients for
(solid curves). Like the previous cases, the NGP and GP results are denoted by black and red curves, respectively. The panels (a), (b) and (c) show the rotationally resolved rate coefficients for  ,
,  and
and  final states of HD and panel (d) presents the rate coefficients summed over all energetically populated rotational and vibrational states. It is seen that the NGP and GP curves are nearly indistinguishable for the total reaction rates (panel d). This is consistent with the results for the H+HD
final states of HD and panel (d) presents the rate coefficients summed over all energetically populated rotational and vibrational states. It is seen that the NGP and GP curves are nearly indistinguishable for the total reaction rates (panel d). This is consistent with the results for the H+HD  D+H2 reaction presented in panels (c) and (f) of figure 11. However, we find a small difference between the NGP and GP results for selected rotationally resolved rate coefficients depicted in panels (a), (b), and (c). In the ultracold regime the NGP and GP rates differ by a factor of 1.5 for
D+H2 reaction presented in panels (c) and (f) of figure 11. However, we find a small difference between the NGP and GP results for selected rotationally resolved rate coefficients depicted in panels (a), (b), and (c). In the ultracold regime the NGP and GP rates differ by a factor of 1.5 for  and
and  , and a factor of 1.2 for
, and a factor of 1.2 for 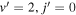 . These differences are minute compared to the rotationally resolved rate coefficients for the hydrogen exchange reaction in H+HD. The effect vanishes for collision energies above 1 K. Although a shape resonance similar to that of the H+HD reaction occurs near 3 K, the magnitude of the GP and NGP rate coefficients remains the same at the resonance position. This shape resonance is associated with the l = 2 partial wave and a Lorentzian least-squares fit gives a resonance energy of 3.33 K and a width of
. These differences are minute compared to the rotationally resolved rate coefficients for the hydrogen exchange reaction in H+HD. The effect vanishes for collision energies above 1 K. Although a shape resonance similar to that of the H+HD reaction occurs near 3 K, the magnitude of the GP and NGP rate coefficients remains the same at the resonance position. This shape resonance is associated with the l = 2 partial wave and a Lorentzian least-squares fit gives a resonance energy of 3.33 K and a width of 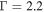 K (or lifetime
K (or lifetime  ). Like the H+HD
). Like the H+HD  D+H2 reaction, for most of the final states we find the values of
D+H2 reaction, for most of the final states we find the values of  to be close to unity but the ratio between the scattering amplitudes for the looping and direct pathways are significantly less than 1 indicating the dominance of the direct pathway.
to be close to unity but the ratio between the scattering amplitudes for the looping and direct pathways are significantly less than 1 indicating the dominance of the direct pathway.
Figure 13. Rotationally resolved and total rate coefficients for the D+H2 H+HD reaction as functions of the incident collision energy. Panels (a), (b) and (c) represent the rotationally resolved reaction rate coefficients for
H+HD reaction as functions of the incident collision energy. Panels (a), (b) and (c) represent the rotationally resolved reaction rate coefficients for  ,
,  and
and  of HD. Panel (d) shows the total rate coefficient. The solid black and red curves refer to NGP and GP rate coefficients that include contributions for
of HD. Panel (d) shows the total rate coefficient. The solid black and red curves refer to NGP and GP rate coefficients that include contributions for  . The corresponding dotted curves include contributions from
. The corresponding dotted curves include contributions from  . The gauge invariance test is shown by the dotted green curve which is also restricted to contributions from
. The gauge invariance test is shown by the dotted green curve which is also restricted to contributions from  .
.
Download figure:
Standard image High-resolution imageThe gauge invariance test for this reaction is shown by the dotted green curve in figure 13. To save computational time the gauge invariance calculation was restricted to total angular momentum  . For a one-to-one comparison, we also show the corresponding GP and NGP results by the dotted red and black curves for
. For a one-to-one comparison, we also show the corresponding GP and NGP results by the dotted red and black curves for 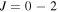 . It is seen that NGP and gauge invariance calculations yield almost indistinguishable results demonstrating that any difference between the GP and NGP results are indeed real and not a numerical artifact.
. It is seen that NGP and gauge invariance calculations yield almost indistinguishable results demonstrating that any difference between the GP and NGP results are indeed real and not a numerical artifact.
4. Summary and conclusions
We have presented a detailed investigation of geometric phase effects in the hydrogen exchange and chemically reactive channels in H+HD( ) collisions at energies ranging from 1 μK to 100 K. Total angular momentum quantum numbers
) collisions at energies ranging from 1 μK to 100 K. Total angular momentum quantum numbers 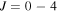 are included to yield rate coefficients converged with respect to partial wave sum for energies up to 20 K. The geometric phase effect is included using the general vector potential approach in a time-independent quantum dynamics method based on hyperspherical coordinates. Our results indicate the presence of large GP effects in the hydrogen exchange channel, yielding rate coefficients that differ by more than two orders of magnitude compared to calculations that do not include the geometric phase. Depending on the final rotational level of the HD molecule, the GP effect is found to enhance or suppress the rate coefficients. In the ultracold regime, the enhancement or suppression of the rate coefficient due to the GP effect is attributed to constructive or destructive interference between the purely nonreactive and exchange scattering amplitudes that encircle the conical intersection. The GP effect persists for energies up to about 3 K beyond which the partial wave summation averages it out. In contrast, we observe no GP effect in the chemically reactive channel leading to the D+H2 product. This is attributed to the direct nature of the reaction with very small amplitudes for the looping scattering pathway resulting in no observable interference effect between the two scattering amplitudes. A similar conclusion is reached for the reverse reaction, D+H2
are included to yield rate coefficients converged with respect to partial wave sum for energies up to 20 K. The geometric phase effect is included using the general vector potential approach in a time-independent quantum dynamics method based on hyperspherical coordinates. Our results indicate the presence of large GP effects in the hydrogen exchange channel, yielding rate coefficients that differ by more than two orders of magnitude compared to calculations that do not include the geometric phase. Depending on the final rotational level of the HD molecule, the GP effect is found to enhance or suppress the rate coefficients. In the ultracold regime, the enhancement or suppression of the rate coefficient due to the GP effect is attributed to constructive or destructive interference between the purely nonreactive and exchange scattering amplitudes that encircle the conical intersection. The GP effect persists for energies up to about 3 K beyond which the partial wave summation averages it out. In contrast, we observe no GP effect in the chemically reactive channel leading to the D+H2 product. This is attributed to the direct nature of the reaction with very small amplitudes for the looping scattering pathway resulting in no observable interference effect between the two scattering amplitudes. A similar conclusion is reached for the reverse reaction, D+H2 H+HD for which some illustrative results are presented. In this case, rotationally resolved rate coefficients for some final HD states exhibit a small GP effect in the ultracold regime but it vanishes in the total rate coefficients. Our calculations also reveal the presence of a reactive scattering resonance in both the hydrogen exchange and chemically reactive channels. Experimental verification of the resonance may provide a sensitive probe of GP effect in H+HD collisions.
H+HD for which some illustrative results are presented. In this case, rotationally resolved rate coefficients for some final HD states exhibit a small GP effect in the ultracold regime but it vanishes in the total rate coefficients. Our calculations also reveal the presence of a reactive scattering resonance in both the hydrogen exchange and chemically reactive channels. Experimental verification of the resonance may provide a sensitive probe of GP effect in H+HD collisions.
Acknowledgments
BKK acknowledges that part of this work was done under the auspices of the US Department of Energy under Project No. 20140309ER of the Laboratory Directed Research and Development Program at Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Los Alamos National Security, LLC, for the National Security Administration of the US Department of Energy under contract DE-AC52-06NA25396. The UNLV team acknowledges support from the Army Research Office, MURI grant No. W911NF-12-1-0476 and the National Science Foundation, grant No. PHY-1505557.