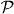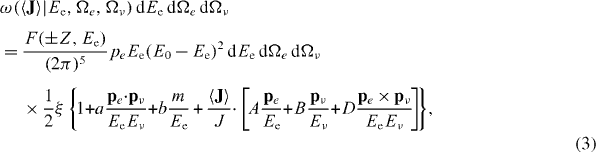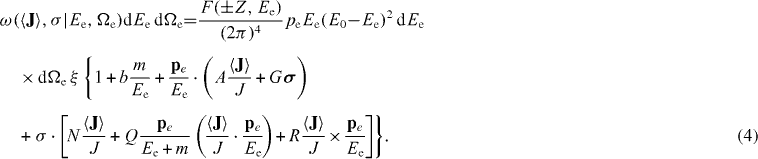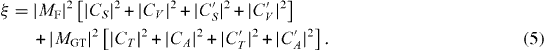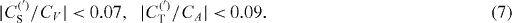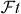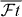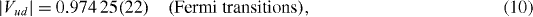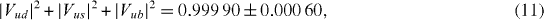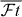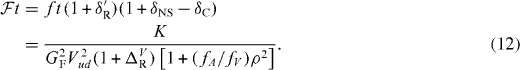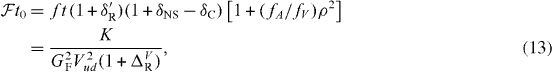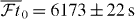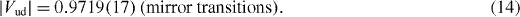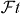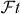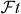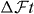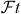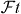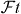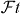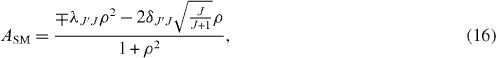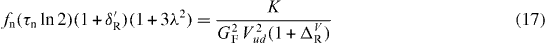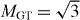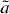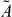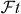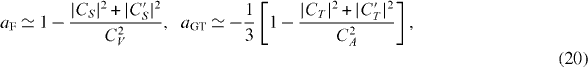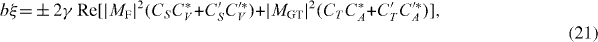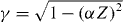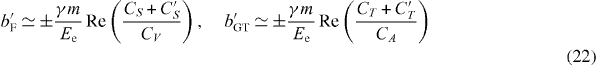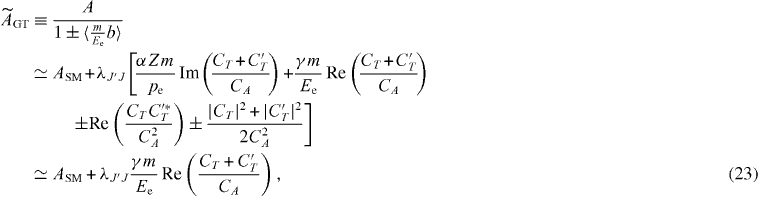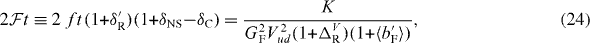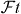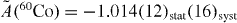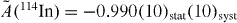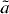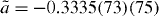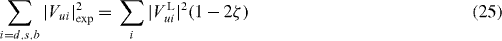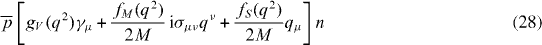Structure and symmetries of the weak interaction in nuclear beta decay

The most general interaction Hamiltonian density describing nuclear β-decay and including all possible interaction types consistent with Lorentz invariance, is expressed in terms of the Dirac γ matrices as [16, 17]

$$\begin{eqnarray} {\cal H}_{\beta} & = & \left(\bar{p} n \right) \left(\bar{e}\left[C_S + C_S^\prime \gamma_5 \right]\nu \right)\nonumber \\ & & + \left(\bar{p} \gamma _\mu n \right) \left(\bar{e} \gamma_\mu \left[C_V + C_V^\prime \gamma_5 \right] \nu \right)\nonumber \\ & & + \frac{1}{2} \left(\bar{p} \sigma _{\lambda \mu} n \right)\left(\bar{e} \sigma _{\lambda \mu} \left[C_T + C_T^\prime\gamma _5\right] \nu \right) \nonumber \\ & & - \left(\bar{p} \gamma _\mu \gamma _5 n \right) \left(\bar{e} \gamma _\mu \gamma _5 \left[C_A + C_A^\prime \gamma _5\right] \nu \right) \nonumber \\ & & + \left(\bar{p} \gamma _5 n \right) \left(\bar{e} \gamma _5\left[C_P + C_P^\prime \gamma _5 \right]\nu \right)\nonumber \\ & & + ~{\rm H.c.}\end{eqnarray} \tag{ 1 }$$

with the tensor operator

$$\begin{eqnarray} \sigma _{\lambda \mu} & = & - \frac{\mathrm{i}}{2} \left(\gamma _\lambda \gamma _\mu - \gamma _\mu \gamma _\lambda \right). \end{eqnarray} \tag{ 2 }$$

This current–current four-fermions point interaction description is valid since the energies available in nuclear β-decay are much smaller than the mass of the W gauge bosons. The interacting fields are associated with the nucleons and the leptons. The interactions are described by five operators called after their transformation properties: the scalar 1 (S), the vector γ_μ (V ), the tensor $\sigma _{\lambda \mu }\sqrt {2}$ (T), the axial vector −i γ_μγ₅ (A), and the pseudoscalar γ₅(P). The amplitudes of the interactions are determined by the coefficients (or coupling constants) C_i and C'_i. These can be complex if time reversal symmetry is violated, leading to a total of 20 real parameters which determine the properties of the Hamiltonian under the discrete symmetries of parity ($\mathcal {P}$), charge conjugation ($\mathcal {C}$) and time reversal ($\mathcal {T}$). The relative values of C_i and C'_i for a given interaction type are fixed by the behavior of that interaction with respect to the parity operation.

The coupling constants C_i and C'_i have to be determined from experiments. To this end Jackson et al [17] have calculated decay rate distributions for allowed transitions including Coulomb corrections. These include terms that involve correlations between the kinematic quantities in the β-decay process, namely, the total energies E_i and momenta p_i of the decay products, with i = R,e and ν_e for the daughter nucleus, the β particle, and the neutrino, respectively. These correlations may also include the initial polarization vector, J, of the decaying system and the polarization direction σ of the β particle.

The angular distribution of the electron and the neutrino from the decay of a polarized nucleus is written as [17]

$$\begin{eqnarray} && \omega(\langle {\bf J} \rangle \vert E_{\mathrm{e}}, \Omega _e, \Omega_\nu)\, \mathrm{d}E_{\mathrm{e}}\,\mathrm{d}\Omega _e\,\mathrm{d}\Omega _\nu \nonumber \\\ms\ms &= & \frac{F(\pm Z, E_{\mathrm{e}})}{(2\pi)^5} p_e E_{\mathrm{e}} (E_0 - E_{\mathrm{e}})^2\, \mathrm{d}E_{\mathrm{e}}\,\mathrm{d}\Omega _e\,\mathrm{d}\Omega _\nu \nonumber \\\ms\ms & &\times \frac{1}{2} \xi \left\{\! 1 {+} a \frac{{\bf p}_e {\cdot} {\bf p}_\nu}{E_{\mathrm{e}} E_\nu} {+} b \frac{m}{E_{\mathrm{e}}}+ \frac{\langle {\bf J} \rangle}{J} {\cdot} \left[\! A \frac{{\bf p}_e}{E_{\mathrm{e}}} {+} B \frac{{\bf p}_\nu}{E_\nu} {+} D \frac{{\bf p}_e \times {\bf p}_\nu}{E_{\mathrm{e}} E_\nu} \!\right] \!\right\}\!,\!\nonumber \\ \end{eqnarray} \tag{ 3 }$$

where the upper (lower) sign refers to β⁻(β⁺) decay, Z is the atomic number of the daughter isotope, E₀ the total β-decay endpoint energy, and m the electron mass. The distribution in electron energy and angle and in the electron polarization direction σ from polarized nuclei is given by

$$\begin{eqnarray} && \omega(\langle {\bf J} \rangle, \sigma \vert E_{\mathrm{e}}, \Omega_{\mathrm{e}}) \mathrm{d}E_{\mathrm{e}}\,\mathrm{d}\Omega_{\mathrm{e}} {=} \frac{F({\pm} Z, E_{\mathrm{e}})}{(2\pi)^4} p_{\mathrm{e}} E_{\mathrm{e}} (E_0 {-} E_{\mathrm{e}})^2\, \mathrm{d}E_{\mathrm{e}} \nonumber \\\ms\ms &&\quad \times\mathrm{d}\Omega_{\mathrm{e}}\,\xi \left\{ 1 + b \frac{m}{E_{\mathrm{e}}} + \frac{{\bf p}_e}{E_{\mathrm{e}}} \cdot \left(A \frac{\langle {\bf J} \rangle}{J} + G \boldsymbol{\sigma } \right) \right. \nonumber \\\ms\ms &&\quad+ \left. \sigma \cdot \left[ N \frac{\langle {\bf J} \rangle}{J} +Q \frac{{\bf p}_e}{E_{\mathrm{e}} + m} \left(\frac{\langle {\bf J} \rangle}{J} \cdot \frac{{\bf p}_e}{E_{\mathrm{e}}}\right)+ R \frac{\langle {\bf J} \rangle}{J} \times \frac{{\bf p}_e}{E_{\mathrm{e}}} \right]\right\}\!.\quad \end{eqnarray} \tag{ 4 }$$

The correlations between the spins and momenta in the above equations are scalar, pseudoscalar or mixed products of the kinematic vectors. They fix the sensitivity of each term to the dimensionless correlation coefficients a,b,A,B,D,G,R, etc, which depend on the Fermi, M_F, or Gamow–Teller, M_GT, nuclear matrix elements involved and on the coupling constants [17]. The factor ξ is given by

$$\begin{eqnarray} \xi & = & \vert M_{\mathrm{F}} \vert ^2 \left[ \vert C_S \vert ^2 + \vert C_V \vert ^2 + \vert C^\prime _S \vert ^2 + \vert C^\prime _V \vert ^2 \right] \nonumber \\ & & + \vert M_{\mathrm{GT}} \vert ^2 \left[ \vert C_T \vert ^2 + \vert C_A \vert ^2 + \vert C^\prime _T \vert ^2 + \vert C^\prime _A \vert ^2 \right] . \end{eqnarray} \tag{ 5 }$$

The scalar and vector interactions contribute to Fermi transitions, while axial-vector and tensor interactions contribute to Gamow–Teller transitions. For pure Fermi or Gamow–Teller transitions the correlation coefficients become, to first order, independent of the nuclear matrix elements thus allowing the extraction of precise information on the coupling constants.

Since the Fierz interference term, b, does not depend on any particular spin or momentum vector it is an integral part of most correlation measurements in β-decay. The actual quantity that is then determined experimentally is usually not X but

$$\begin{equation} \tilde{X} = \frac{X} { 1 + \langle b^\prime \rangle } \end{equation} \tag{ 6 }$$

with X = a,A,B,D,R, etc, and b' ≡ (m/E_e)b and where 〈 〉 stands for the weighted average over the observed part of the β spectrum.

Note that when correlation coefficients are determined with a precision of the order of several 10⁻³, higher-order effects have to be taken into account. The major ones are radiative corrections [18, 19], electromagnetic corrections [20, 21], and the so-called recoil terms, related to matrix elements induced by the fact that the decaying quark in the β-decay process is not a free particle but is bound inside a nucleon interacting with other quarks [20, 22] (section 9.1).

The SM involves only V and A currents, assumes maximal violation of parity and charge conjugation and has no other $\mathcal {CP}$ (or $\mathcal {T}$) violation mechanism than the one related to the phase in the Cabibbo–Kobayashi–Maskawa (CKM) quark-mixing matrix [1, 23]. Effects related to this phase are not expected to contribute to observables in nuclear β-decay at the present level of precision [24]. For the coupling constants this implies C_V /C'_V  = 1, C_A/C'_A = 1, C_S = C'_S = C_T  = C'_T  = C_P  = C'_P  = 0, and Im(C^(')_i) = 0 for all i. Further, C_V  = 1 as the conserved vector current (CVC) hypothesis [25] implies that the vector current coupling constant is not renormalized in the nuclear medium, so that the V part of the weak interaction is universal. The axial current, on the other hand, is not a conserved current and a value C_A = −1.2701(25) [1] can be obtained from measurements in neutron decay. Note that the pseudoscalar term in equation (1) does not contribute to experimental observables in nuclear β-decay or neutron decay at the present level of precision as the pseudoscalar hadronic current $\bar {p} \gamma _5 n$ vanishes in the non-relativistic treatment of nucleons.

The most recent global fit [3] of selected experimental results in nuclear β-decay and neutron decay yielded the following limits on the amplitude of S and T coupling constants (assumed to be real) relative to the V and A coupling constants (at 95.5% CL):

$$\begin{equation} \vert C^{(')}_{\mathrm{S}}/C_V \vert < 0.07 , ~ ~ \vert C^{(')}_{\mathrm{T}}/C_A \vert < 0.09 . \end{equation} \tag{ 7 }$$

In the remainder of this paper an overview will be given of recent and ongoing efforts to investigate the structure and symmetries of the weak interaction in nuclear β-decay. This will consist of three major parts, namely: (i) the determination of the quark-mixing matrix element V_ud; (ii) correlation measurements searching for scalar and tensor components in the weak interaction; and (iii) correlation measurements investigating the parity and time-reversal symmetries. Further, a short overview of the status and prospects of searches for Lorentz invariance violation and SCC in nuclear β-decay will also be given. Finally, some important challenges for this field that will provide improved sensitivity to the physics being investigated, are discussed as well.

For many years the ft-values of the 0⁺ → 0⁺ superallowed Fermi transitions have been the subject of intensive research. These transitions are of pure vector character and with the validity of the CVC hypothesis, all these transitions should have the same decay strength, provided nucleus-dependent corrections are duly taken into account. This is expressed by the corrected ${\cal F}t$-value [26]

$$\begin{equation} 2 {\cal F}t \equiv 2\,ft (1+\delta^\prime_{\mathrm{R}})(1+\delta_{\rm NS}-\delta_{\mathrm{C}}) =\frac{K}{G^2_{\mathrm{F}} V^2_{ud} (1+\Delta_{\mathrm{R}}^V)} \end{equation} \tag{ 8 }$$

with f the statistical rate function, t the partial half-life of the transition, δ'_R and δ_NS transition-dependent radiative corrections, and δ_C the isospin-symmetry-breaking correction. Further, K/(ℏc)⁶ = 2π³ℏ ln 2/(m_ec²)⁵ = 8120.2776(9) × 10⁻¹⁰ GeV⁻⁴ s [1], G_F is the Fermi coupling constant deduced from muon decay [1] G_F/(ℏc)³ = 1.166 378 7(6) × 10⁻⁵ GeV⁻², and Δ^V _R = (2.361 ± 0.038)% is a nucleus-independent radiative correction [27]. All terms on the left-hand side—including the factor 2 which arises from the square of the Fermi matrix element for these transitions—are related to a given nuclear β transition, whereas the right-hand side contains only fundamental constants and the radiative correction, Δ^V _R, which is the same for all semi-leptonic processes. Three experimental quantities have to be determined to extract the ${\cal F}t$-value: the Q_EC value, which determines the statistical rate function f, the branching ratio, BR, and the half-life, t_1/2. The latter two determine, together with the electron-capture-to-positron ratio, P_EC, the partial half-life of the β transition

$$\begin{equation} t = \frac{t_{1/2}} {\mathrm{BR}} \left(1 + P_{\mathrm{EC}} \right) . \end{equation} \tag{ 9 }$$

The current average ${\cal F}t$-value for the set of 13 best known pure Fermi transitions is $\overline {{\cal F}t} = (3071.81\pm 0.83)\,\mathrm {s}$ [26], providing a test of the CVC hypothesis at the 3 × 10⁻⁴ level. This high precision is due in part to (a) the excellent precisions and accuracies that were recently obtained for the Q_EC values of these transitions with Penning trap mass spectrometry [28, 29]; (b) advanced spectroscopic methods, including multi-detector set-ups and very precisely calibrated detectors for measuring half-lives and branching ratios [30–33]; and (c) improved theoretical calculations of the different corrections involved [27, 34, 35]. The above $\overline {{\cal F}t}$ value corresponds to [26]

$$\begin{equation} |V_{ud}| = 0.974\,25(22) \quad {\rm (Fermi\ transitions),} \end{equation} \tag{ 10 }$$

where the uncertainty is dominated by the theoretical corrections. Combining this with the value of V_us = 0.2252(9) deduced from K-decays [1, 36] and ignoring the V_ub matrix element which is negligibly small, the unitarity test on the first row of the CKM matrix results in [36]

$$\begin{equation} |V_{ud}|^2 + |V_{us}|^2 + |V_{ub}|^2 = 0.999\,90\pm 0.000\,60, \end{equation} \tag{ 11 }$$

where V_ud and V_us contribute by equal amounts to the uncertainty.

With the unitarity of the CKM matrix thus being tested at the 6 × 10⁻⁴ level, strong limits can be deduced for different types of physics beyond the SM [8, 9, 26, 36, 37]. It is important to further reduce the uncertainty on V_ud, thereby increasing the sensitivity to new physics. Presently, the uncertainty on the nucleus-independent radiative correction Δ_R^V [27] is the dominant contribution to the error budget of V_ud. The uncertainties from experiments and from the nuclear-structure-dependent corrections, δ_C and δ_NS, together contribute almost as much. A continued effort for new and more precise measurements, as well as improved theoretical calculations of the parameters contributing to $\overline {{\cal F}t}$ is thus required. On the experimental side, data for the already well-known transitions can be made more precise and new cases can be added [26]. On the theory side nuclear-structure-dependent corrections can be further tested by experiment [38], thus providing improvements in the theoretical understanding of these corrections [35]. At some point the calculation of the correction Δ_R^V is expected to be further improved as well. Finally, as V_ud and V_us both contribute by comparable amounts to the uncertainty of the unitarity test (equation (11)), efforts to improve the accuracy of V_us are also required. Note that in this case the dominant contributions to the error comes from the semi-leptonic vector form factor f₊(0) in the K → π hadronic matrix element, and the ratio of the pseudoscalar decay constants f_K and f_π, that are both obtained from theoretical calculations (see e.g. [36]).

It was recently pointed out [39] that V_ud can also be obtained from the superallowed β transitions between T = 1/2 isospin doublets in mirror nuclei. These so-called mirror transitions are mixed, with both Fermi and Gamow–Teller contributions. Since the axial-vector weak current is not conserved, an additional parameter has to be determined experimentally in order to extract the Fermi/Gamow–Teller mixing ratio ρ ≡ (C_AM_GT)/(C_V M_F) that enters the equation of the corrected ft-values [40]

$$\begin{eqnarray} {\cal F}t &=& ft (1+\delta^\prime_{\mathrm{R}})(1+\delta_{\rm NS}-\delta_{\mathrm{C}}) \nonumber\\ &=& \frac{K}{G^2_{\mathrm{F}} V^2_{ud} (1+\Delta_{\mathrm{R}}^V) \left[ 1 + (f_A/f_V)\rho^2 \right] }. \end{eqnarray} \tag{ 12 }$$

Rearranging this equation on can define ${\cal F}t_0$ so that

$$\begin{eqnarray} {\cal F}t_0 &=& ft (1+\delta^\prime_{\mathrm{R}})(1+\delta_{\rm NS}-\delta_{\mathrm{C}}) \left[ 1 + (f_A/f_V)\rho^2 \right] \nonumber\\ &=& \frac{K}{G^2_{\mathrm{F}} V^2_{ud} (1+\Delta_{\mathrm{R}}^V)} , \end{eqnarray} \tag{ 13 }$$

where, similar to equation (8), the left-hand side includes all transition-dependent terms, with f_V and f_A the statistical rate functions for the V and A parts respectively. Using available experimental data for the values of ρ for the mirror decays of ¹⁹Ne, ²¹Na, ²⁹P, ³⁵Ar and ³⁷K, the average value for these decays was found to be $\overline {{\cal F}t}_0 = 6173\pm 22 \, {\rm s}$. This provided a new independent test of CVC at the 4 × 10⁻³ level [39] and enabled the extraction of the value

$$\begin{equation} |V_{\mathrm{ud}}| = 0.9719(17) \, {\rm (mirror\ transitions)}. \end{equation} \tag{ 14 }$$

The error is here dominated by the statistical uncertainties in the mixing ratios ρ. The most sensitive observables used so far to extract ρ are the β–ν angular correlation, a, and the β-asymmetry parameter, A. The precision obtained for |V_ud| depends then on uncertainties of the ${\cal F}t$ value and of the mixing ratio ρ, i.e. on the precision that is reached in the measurements of a or A.

The SM expression for the β–ν angular correlation coefficient is [17]

$$\begin{equation} a_{\mathrm{SM}} = \frac{1 - \rho^2/3}{1 + \rho^2}. \end{equation} \tag{ 15 }$$

The ongoing and planned β–ν correlation measurements in mirror nuclei with trap-based set-ups [41–46], combined with new, precise determinations of Q_EC values, via mass measurements using Penning traps, of branching-ratios and of half-lives for mirror transitions [47–51] will allow further improvements in precision. This is shown in columns 2–4 of table 1 which lists the precision on |V_ud| that is obtained, using equation (13), when combining the ${\cal F}t$-values for the mirror β transitions with values for the mixing ratio ρ extracted from measurements of the β–ν correlation coefficient a with a relative precision of 0.5%. A precision of this order has already been reached in several recent measurements [52, 53] and ongoing and planned experiments aim for precisions at the few per mille level. Table 1 shows for each case the precision on |V_ud| that is obtained with the current ${\cal F}t$-value for the particular mirror transition [40], and the precision that would be obtained if the error on the ${\cal F}t$-value would not contribute to the error on |V_ud| anymore. The corresponding factor by which the precision on the ${\cal F}t$-value has to be improved for this is also listed. If this factor is smaller than unity it means that the ${\cal F}t$-value is already sufficiently well known for this purpose and that in fact the 0.5% relative precision assumed for the a or A parameter is the limiting factor in that case.

Table 1. Precision on |V_ud| obtained from the individual mirror nuclei when the β–ν correlation coefficient a (columns 2–4), respectively the β-asymmetry parameter A (columns 5–7) are determined with a relative precision of 0.5%. Columns 2 and 5 list the precision on |V_ud| when the actual ${\cal F}t$-values for the mirror transitions [40] are used. Columns 3 and 6 list the precision on |V_ud| when the ${\cal F}t$-value would be sufficiently well known such that it would not contribute to the error on |V_ud| anymore. The factor by which the ${\cal F}t$-values have to be improved to reach this situation are listed in columns 4 and 7, respectively. For ¹⁹Ne the new value ${\cal F}t = 1721.5(17)$ s was used which includes, apart from the data listed in [40], also the new mass excess from [54] and the new half-life from [51].

Parent nucleus	ΔVud	a		ΔVud	A
		(ΔVud)limit	Factor $\Delta {\cal F}t$		(ΔVud)limit	Factor $\Delta {\cal F}t$
3H	0.0011	0.0010	2.1	0.0011	0.0009	2.3
11C	0.0025	0.0016	4.0	0.0207	0.0207	0.3
13N	0.0017	0.0017	1.0	0.0123	0.0123	0.1
15O	0.0020	0.0016	2.4	0.0023	0.0020	1.9
17F	0.0019	0.0013	3.1	0.0341	0.0341	0.1
19Ne	0.0011	0.0010	1.5	0.0011	0.0011	1.5
21Na	0.0022	0.0017	2.7	0.0036	0.0034	1.3
23Mg	0.0025	0.0018	3.1	0.0034	0.0030	1.9
25Al	0.0019	0.0018	1.7	0.0056	0.0056	0.5
27Si	0.0029	0.0018	4.1	0.0068	0.0066	1.1
29P	0.0026	0.0018	3.4	0.0024	0.0014	4.3
31S	0.0038	0.0018	5.9	0.0068	0.0061	1.8
33Cl	0.0021	0.0018	2.0	0.0013	0.0006	6.0
35Ar	0.0019	0.0018	1.1	0.0007	0.0004	4.8
37K	0.0034	0.0017	5.8	0.0050	0.0041	2.3
39Ca	0.0024	0.0016	3.5	0.0032	0.0027	2.2
41Sc	0.0029	0.0022	2.7	0.0299	0.0299	0.2
43Ti	0.0076	0.0018	13.2	0.0167	0.0151	1.6
45V	0.0112	0.0020	17.7	0.0115	0.0032	11.2

As can be seen from table 1, for the β–ν correlation coefficient, the most sensitive cases are ³H and ¹⁹Ne for which absolute errors on |V_ud| of 0.0011 can be reached with the current ${\cal F}t$-values for these isotopes, and 0.0010 when the ${\cal F}t$-values are improved by a factor of 1.5 for ¹⁹Ne, or a factor of 2 for ³H. This is to be compared to the value of 0.000 22 that is obtained from the current full set of superallowed Fermi transitions. For ¹⁷F an absolute precision of 0.0013 can be obtained if the ${\cal F}t$-value is improved by a factor of 3. A measurement of a with ¹⁹Ne, one of the most sensitive cases, is currently being prepared at GANIL [46]. Work is also ongoing to improve the ${\cal F}t$-value. Besides the recently published new Q_EC value [54] and new half-life [51] for this transition, two more half-life measurements—one at GANIL, resulting in a preliminary value t_1/2 = 17.254(5) s [55] and the other at KVI-Groningen, with a preliminary value t_1/2 = 17.283(8) s [56]—have recently been performed, along with a new measurement of the branching ratio at TRIUMF [57].

Note that for almost all other mirror nuclei listed, a 0.5% measurement of a yields values for |V_ud| with an absolute error between 0.0016 and 0.0018 provided their ${\cal F}t$-values are improved by a factor of 2–4. As a consequence, there is a strong interest in improving the precision of the ${\cal F}t$-values for all mirror nuclei. New measurements of Q-values, branching ratios and half-lives for the mirror β transitions are not only important to increase the precision of the ${\cal F}t$-values but also to cross-check on the sometimes rather old experimental data, as is the case with ¹⁹Ne, so as to also improve their reliability.

A similar analysis of sensitivity to |V_ud| can also be performed for measurements of the β-asymmetry parameter A for the mirror nuclei. The general SM expression for this coefficient is

$$\begin{eqnarray} &&A_{\mathrm{SM}} = \frac{ \mp \lambda_{J^\prime J} \rho^2 - 2 \delta_{J^\prime J} \sqrt{\frac{J}{J+1}} \rho } {1 + \rho^2}, \end{eqnarray} \tag{ 16 }$$

with λ_J'J = 1 for J → J − 1, λ_J'J = 1/(J + 1) for J → J and λ_J'J = −J/(J + 1) for J → J + 1 transitions, and δ_J'J the Kronecker delta. For a mirror transition, λ_J'J = 1/(J + 1) and δ_J'J = 1. The results of this analysis are listed in columns 5–7 of table 1. Whereas it turns out that the β-asymmetry parameter for the mirror transitions is in most cases less sensitive to |V_ud| than the β–ν angular correlation coefficient, a few transitions provide an even higher sensitivity. As can be seen, in determining A with a precision of 0.5%, an absolute precision on |V_ud| of 0.0011 can again be obtained with ¹⁹Ne, while measurements of the A parameter for ³H, ³³Cl and ³⁵Ar yield even higher precisions, with absolute uncertainties of 0.0009, 0.0006 and 0.0004 respectively. Note that the latter is only about twice larger than the uncertainty of 0.000 22 obtained from the current entire set of superallowed Fermi decays. In order to reach these precisions, the ${\cal F}t$-values for these four mirror transitions have to be improved by factors between 1.5 and 6 (table 1). However, already with the currently available ${\cal F}t$-values [40] uncertainties on |V_ud| ranging between 0.0007 and 0.0013 can be obtained. Also, with the isotopes ¹⁵O and ²⁹P precisions similar to those accessible with the β–ν correlation can be obtained.

Apart from the requirement that a correlation measurement has to performed, mirror transitions depend on the same radiative corrections, δ'_R and Δ_R^V in equation (12), and nuclear-structure corrections, δ_NS and δ_C, as the superallowed Fermi transitions. On the other hand this set of mirror nuclei extends the number of transitions from which information on the value of |V_ud| can be obtained. With the precision of |V_ud| from mirror transitions improving, the sensitivity of the CKM unitarity test to new physics will increase, although ultimately this will be limited by the knowledge of the radiative correction Δ_R^V, similar to the superallowed Fermi transitions and neutron decay. When extracting |V_ud| from pion beta decay [36, 58], the attainable sensitivity is dominated by the experimental uncertainty on a very small (order 10⁻⁸) branching ratio.

Neutron decay is the simplest among the T = 1/2 mirror transitions so that it also requires the ratio between the A and V parts, ρ, to be determined. It has the advantage of being a single-nucleon decay so that no nuclear structure effects have to be taken into account. The ft-value can here be written as

$$\begin{equation} f_{\mathrm{n}} (\tau_{\mathrm{n}} \ln{2}) (1+\delta^\prime_{\mathrm{R}}) (1 + 3 \lambda^2) =\frac{K}{G_{\mathrm{F}}^2\,V^{2}_{ud} (1+\Delta_{\mathrm{R}}^V)} \end{equation}\noindent \tag{ 17 }$$

with f_n(1 + δ'_R) the phase space factor including radiative corrections [36], τ_n the neutron lifetime and λ = g_A/g_V  = C_A/C_V the ratio between the axial-vector and the vector weak couplings. Note that λ plays here the role of ρ, with the Fermi and Gamow–Teller matrix elements M_F = 1 and $M_{\mathrm {GT}}=\sqrt {3}$. V_ud can again be extracted by measuring the neutron lifetime and determining λ which is usually done by measuring the β-asymmetry parameter A. Obtaining accurate results for both these quantities has, however, turned out to be difficult and very challenging experimentally [5, 7, 59–61].

The most precise value for the neutron lifetime reported so far, τ_n = 878.5 ± 0.7 ± 0.3 s [62], deviated by about six combined standard deviations from the world average value, τ_n = 885.7 ± 0.8 s [63] and also from the previous most precise measurement, τ_n = 885.4 ± 0.9 ± 0.4 s [64]. Recently, a new measurement was published yielding τ_n = 880.7 ± 1.3 ± 1.2 s [65], in agreement with the result of [62]. Following a new analysis [66] the systematic corrections to the result of [64] were recalculated leading to a significantly lower value of τ_n = 881.6 ± 0.8 ± 1.9 s [67], consistent with the result of [62]. Averaging then the seven most precise measurements of the neutron lifetime to date [62, 65, 67–71] the Particle Data Group proposed the new world average value [1]

$$\begin{equation} \tau_{\mathrm{n}} = 880.1~\pm~1.1\,{\rm s} . \end{equation}\noindent \tag{ 18 }$$

As to the ratio λ, the current world average value is λ = −1.2701(25) [1]. Combining this value with the above mentioned neutron lifetime recommended by the Particle Data Group leads to |V_ud| = 0.9773(17), which is at 1.8 standard deviations from the value |V_ud| = 0.974 25(22) for the superallowed Fermi transitions. It is to be noted, however, that the individual values for λ, most of which were deduced from measurements of the β-asymmetry parameter, vary quite a bit. The three oldest results [72–74] are systematically lower than the more recent ones by as much as 3–5% and were, in addition, subject to corrections in the range of 15–30%. Averaging then only the most recent results [75–78] yields λ = −1.2751(12). Combining this value for λ with the world average value for τ_n yields |V_ud| = 0.9741(10), in agreement with the value from the Fermi transitions quoted in equation (10).

Clearly, the issues on the values for τ_n and λ need to be settled by new, precise and accurate measurements.

Recent correlation measurements in nuclear β-decay searching for scalar and/or tensor currents have concentrated mainly on the β–ν correlation, a(p_e·p_ν)/E_eE_ν, and the β-asymmetry parameter, A(J·p_e)/E_e. Note that the actually determined experimental observables, $\tilde {a}$ and $\tilde {A}$ (equation (6)), also include the Fierz interference term. The Fermi part of the latter is, in addition, also constrained by the ${\cal F}t$-value of the superallowed pure Fermi transitions.

4.1.1. β–ν angular correlation.

For mixed Fermi/Gamow–Teller transitions, and assuming maximal parity violation and time-reversal invariance for the V and A interactions, the β–ν correlation coefficient can be written as [3, 17]

$$\begin{eqnarray} a & \simeq & a_{\mathrm{SM}} - \frac{1}{\left(1 + \rho ^2 \right)^2 } \nonumber \\\ms\ms & &\times\left[ \left(1 {+} \frac{1}{3} \rho ^2 \right) \frac{\vert C_S \vert ^2 {+} \vert C^\prime _S \vert ^2}{ C_V ^2} {+} \frac{1}{3} \rho ^2 \left(1 {-}\rho ^2 \right) \frac{\vert C_T \vert ^2 {+} \vert C^\prime _T \vert ^2}{ C_A ^2} \right] \nonumber \\\ms\ms & & + \frac{\alpha Z m}{p_{\mathrm{e}}} \frac{1}{ 1 + \rho ^2 } \left[ \mp \mathrm{Im} \left(\frac{ C_S + C^\prime _S }{ C_V } \right) \pm \frac{ \rho ^2 }{ 3 } \mathrm{Im} \left(\frac{ C_T + C^\prime _T }{ C_A } \right)\right]\nonumber \\ \end{eqnarray} \tag{ 19 }$$

with a_SM given by equation (15). The last line represents the Coulomb correction up to order αZ with α the fine structure constant. For pure Fermi and pure Gamow–Teller transitions this reduces to

$$\begin{eqnarray} &&a_{\mathrm{F}} \simeq 1 - \frac{\vert C_S \vert ^2 + \vert C^\prime _S \vert ^2}{ C_V ^2},~~ a_{\mathrm{GT}} \simeq -\frac{1}{3} \left [ 1 - \frac{\vert C_T \vert ^2 + \vert C^\prime _T \vert ^2}{ C_A ^2} \right ],\nonumber \\ \end{eqnarray}\noindent \tag{ 20 }$$

respectively.

4.1.2. Fierz interference term.

The Fierz interference term has the form [17]

$$\begin{eqnarray} &&b \xi {=} \pm 2 \gamma \,\mathrm{Re} [ \vert M_{\mathrm{F}} \vert ^2 (C_S C_V^* {+} C_S^\prime C_V^{\prime *}) {+} \vert M_{\mathrm{GT}} \vert ^2 (C_T C_A^* {+} C_T^\prime C_A^{\prime *}) ] ,\!\!\nonumber \\ \end{eqnarray} \tag{ 21 }$$

with $\gamma = \sqrt { 1 - \left ({\alpha Z} \right)^2 }$. Assuming again maximal parity violation and time-reversal invariance for the V and A interactions this reduces to

$$\begin{eqnarray} &&b^{\prime}_{\mathrm{F}} \simeq \pm \frac{\gamma m}{E_{\mathrm{e}}} \, \mathrm{Re} \left(\frac{C_S + C^{\prime}_S}{C_V}\right),\quad b^{\prime}_{\mathrm{GT}} \simeq \pm \frac{\gamma m}{E_{\mathrm{e}}}\,\mathrm{Re} \left(\frac{C_T + C^{\prime}_T}{C_A}\right)\nonumber \\ \end{eqnarray}\noindent \tag{ 22 }$$

for the Fermi and Gamow–Teller parts, respectively.

Note that the Fierz interference term depends linearly on the exotic couplings in contrast to the quadratic dependence for the β–ν correlation so that both observables complement each other. The quadratic dependence for the β–ν correlation, however, requires a higher experimental precision be reached in order to obtain a similar sensitivity to new physics as the Fierz interference term.

4.1.3. β-asymmetry.

For pure Fermi transitions the β-asymmetry parameter is obviously zero. For pure Gamow–Teller transitions and allowing for tensor currents, the β-asymmetry parameter can be written as [17, 79]

$$\begin{eqnarray} \skew3\widetilde{A}_{\mathrm{GT}} & \equiv & \frac{A}{1 \pm \langle \frac{m}{E_{\mathrm{e}}}b \rangle } \nonumber \\ & \simeq & A_{\mathrm{SM}} + \lambda_{J^{\prime}J} \left[\! \frac{ \alpha Z m } {p_{\mathrm{e}}} \,{\rm Im} \left(\! \frac{ C_T + C^{\prime}_T }{ C_A }\!\right) {+} \frac{\gamma m} {E_{\mathrm{e}}} \,{\rm Re} \left(\!\frac{C_T + C^{\prime}_T }{ C_A } \!\right) \right. \nonumber \\ &&\quad\left. \pm {\rm Re} \left(\frac{ C_T C^{\prime *}_T} {C_A^2} \right) \pm \frac{ |C_T|^2 + |C^{\prime}_T|^2 }{ 2 C_A^2 }\right] \nonumber \\ & \simeq & A_{\mathrm{SM}} + \lambda_{J^{\prime}J} \frac{\gamma m}{E_{\mathrm{e}}}\, {\rm Re} \left(\frac{ C_T + C^{\prime}_T}{C_A} \right), \end{eqnarray} \tag{ 23 }$$

where maximum parity violation was assumed for the axial-vector part of the interaction and with A_SM = ∓λ_J'J from equation (16). The complete SM prediction should however include recoil, radiative and electromagnetic corrections, which usually play a role at the 10⁻³ precision level. The recoil corrections are determined by the induced form factors [20] and will be addressed in section 9.1.

The approximation in the last line of equation (23) uses the fact that (i) existing limits on the imaginary term, Im(C_T  + C'_T )/C_A, are already at the 1% level [80] what is then neglected, and (ii) the couplings C_T /C_A and C'_T /C_A are presumably small as given by equation (7), such that second-order terms like |C_T |²/|C_A|² were neglected. Any departure in the measured value $\tilde {A}$ from the SM prediction then provides information on the tensor couplings (C_T  + C'_T ) via b_GT. The factor γ is of order unity so that the sensitivity to these tensor couplings is enhanced for transitions with low endpoint energy.

4.2.1. Fermi transitions.

Allowing for scalar weak currents, and thus for a non-zero Fierz interference term, the ${\cal F}t$-value for superallowed Fermi transitions can be written as

$$\begin{equation} 2 {\cal F}t \equiv 2\,ft (1{+}\delta^\prime_{\mathrm{R}})(1{+}\delta_{\rm NS}{-}\delta_{\mathrm{C}}) =\frac{K}{G^2_{\mathrm{F}} V^2_{ud} (1{+}\Delta_{\mathrm{R}}^V) (1{+}\langle b^\prime_{\mathrm{F}} \rangle)} , \end{equation} \tag{ 24 }$$

with 〈b'_F〉 defined in equation (22). The weighted average ${\cal F}t$-value for the 13 best known superallowed Fermi transitions yields a very strong constraint for the scalar coupling constants, (C_S + C'_S)/C_V  = −0.0022(26) [26].

4.2.2. Gamow–Teller transitions.

In recent years ion and atom traps, that are widely used for atomic and nuclear physics experiments [28, 87, 88], have found a sensitive application for correlation measurements in nuclear β-decay. Traps provide almost ideal source conditions for precision weak interaction experiments. They allow producing isotopically pure and well-localized samples of atoms/ions, at temperatures between room temperature and the few mK range, and in vacuum. Such conditions reduce the effects of scattering of β particles which can be a limitation when radioactive sources are embedded in a material [79, 81] and allow also the detection of the recoil ion. In fact, all four types of traps, namely the magneto-optical atom trap (MOT), Paul and Penning type ion traps, as well as the electrostatic ion beam trap, are now being used for precision weak interaction studies [43, 89–92]. A summary of ongoing or planned β–ν correlation projects along with the most precise results obtained so far is given in table 2.

Table 2. Overview of ongoing or planned β–ν correlation projects. For comparison the most precise already published results are also listed. The name of the team in the third column indicates the leading team although the collaborations can include other institutes. Experiments are ordered according to their state of progress indicated in column 4.

Parent	Technique	Team, laboratory	Remarks	Ref.
6He	Spectrometer	ORNL	a=−0.3308(30)	[93, 94]
32Ar	Foil; p recoil	UW-Seattle, ISOLDE	$\tilde {a}$ = 0.9989(52)(39)	[52]
38mK	MOT	SFU, TRIUMF	$\tilde {a} = 0.9981(30)(34)$	[53]
21Na	MOT	Berkeley, BNL	a=0.5502(38)(46)	[95]
6He	Paul trap	LPC-Caen, GANIL	$\tilde {a} = -0.3335(73)(75)$	[96]
6He	Paul trap	LPC-Caen, GANIL	Analysis under way	[97]
8Li	Paul trap; βα	ANL	Analysis under way	[98, 99]
35Ar	Paul trap	LPC-Caen, GANIL	First data June 2011	[42]
35Ar	Penning trap	Leuven, ISOLDE	First data June 2011	[43]
19Ne	Paul trap	LPC-Caen, GANIL	Ready to take data	[46]
6He	EIBT	Weizmann, SOREQ	In progress	[92]
6He	MOT	ANL, CENPA	In progress	[100]
Ne	MOT	Weizmann, SOREQ	In progress	[45]
21Na	MOT	KVI-Groningen	In progress	[44, 101]
32Ar	Penning trap	Texas A&M	In preparation	[102]
8He	Foil; βγ	NSCL	In preparation	[103]

The experiment with ^38mK at TRIUMF [53], which used a double MOT trap, has produced the most precise result to date. Currently it is being upgraded in view of reaching a sensitivity at the few per mille level [104].

The result recently obtained for ⁶He with the Paul trap at GANIL [96] is currently being further improved as well. To this end, the setup has recently been upgraded and now also allows separating the different charge states produced by shake-off in the β-decay process. Charge-state distribution measurements as well as high-precision β–ν correlation measurements allowing for a statistical precision below 0.5% have in the mean time been performed already with ⁶He [97] and ³⁵Ar [42], while a measurement with ¹⁹Ne is planned [46].

A β–ν correlation project with ³⁵Ar is also being carried out with the WITCH setup [43, 105, 106] at the ISOLDE facility at CERN. Whereas most β–ν correlation measurements observe coincidences between the recoil ions and the β particles the WITCH set-up, which uses a double Penning ion trap and a retardation spectrometer [107, 108], is designed to measure the energy spectrum of the recoil ions in singles. First statistics with ³⁵Ar was obtained in 2011.

For the MOT-based β–ν correlation project with ⁶He at CENPA, a high intensity source of gaseous ⁶He with a rate of  10¹⁰ atoms s⁻¹ has recently been developed [100, 109]. A new high-precision half-life measurement has already been performed with about 500 ⁶He atoms s⁻¹ confined in a simple storage volume [110]. Currently, the setup with the MOT is being installed for the measurement of the β–ν correlation [100].

At the Weizmann Institute two projects for β–ν correlation measurements are currently being prepared. The first will use a electrostatic ion beam trap (EIBT) [111]. ⁶He ions will be trapped in the mirror potential with the ⁶Li recoil ions and the β-decay electrons being observed in coincidence [92]. In the second experiment, neutron-deficient Ne isotopes will be trapped in a MOT and the β–ν correlation will again be deduced by a measurement in coincidences [45].

The β-decay Paul trap [98] that was developed at Argonne National Laboratory aims at determining the β–ν correlation of ⁸Li by inferring the momentum of the neutrino from the kinematic shifts of the breakup α particles following the ⁶Li β decay [99].

The double Penning system that is currently being set up at Texas A&M University [102] will study the β–ν correlation for T = 2 superallowed beta-delayed proton emitters. The first experiment will be with ³²Ar.

Finally, at the NSCL, a precision measurement of the double Doppler shift of the γ rays following the β-decay of ⁸He is planned [103]. This isotope offers a factor of 3 larger sensitivity to non-SM currents than a previous measurement of this type with ¹⁸Ne [112]. The use of a high-efficiency γ multi-detector array will further add to the efficiency.

The emission asymmetry of the daughter (recoil) ions from β-decay has been measured only once till now, in the pure Gamow–Teller decay of ⁸⁰Rb [113]. This observable is proportional to the sum of the β-asymmetry parameter, A, and the neutrino asymmetry parameter, B, [17], A_recoil = −(A + B). Since for pure Gamow–Teller transitions A = −B the recoil asymmetry vanishes in the SM and is exclusively sensitive to tensor interactions: A_recoil = ± 2λ_J'JC_T C'_T /C²_A. The result, A_recoil = 0.015 ± 0.029_stat ± 0.019_syst, although with modest overall precision, places constraints on tensor currents that are complementary to those from other experiments [113]. The systematic error is at present limited by the knowledge of recoil-order corrections (section 9.1). However, it was pointed out [113] that the statistical error can easily be reduced by a factor 2 or more, and it was shown that the momentum dependence can be observed. A new measurement of this observable would be highly valuable.

Assuming the presence of right-handed currents, the unitarity condition for the CKM matrix can be written as [122]

$$\begin{eqnarray} \sum_{i=d, s, b} |V_{ui}|^2_{\rm exp} & = & \sum_{i} |V_{ui}^{\rm L}|^2 (1 - 2 \zeta) \end{eqnarray}\noindent \tag{ 25 }$$

$$\begin{eqnarray} & = & 1 - 2 \zeta, \end{eqnarray}\noindent \tag{ 26 }$$

where V^L_ui are the elements of the CKM matrix for left-handed quarks, which is assumed to be strictly unitary. The most recent analysis of the superallowed Fermi transitions [36] yields ζ = 0.000 05(30), which is to date the most stringent limit on the mixing angle.

The already mentioned determinations of the β-asymmetry parameter in the pure Gamow–Teller decays of ⁶⁰Co [81] and ¹¹⁴In [79] (section 4.2.2), were primarily meant to probe the presence of tensor currents via the Fierz interference term. They also provide limits on right-handed currents. When assuming only V and A interactions and allowing for right-handed couplings, the β-asymmetry parameter can be written as

$$\begin{equation} \tilde{A} \equiv A \simeq \mp \lambda_{J^\prime J} \left[ 1 - 2 \left(\delta + \zeta \right)^2 \right].\end{equation}\noindent \tag{ 27 }$$

The weighted average of the results obtained with ⁶⁰Co and ¹¹⁴In then corresponds to the limit m₂ > 250 GeV/c² (at 90% CL) for ζ = 0. The only existing measurement of the β-asymmetry parameter with a competing sensitivity is that for the mirror transition of ¹⁹Ne reported in [123] (see also [4]). The sensitivity of asymmetry measurements in mirror transitions has been investigated previously already [124]. This showed that, for equal relative experimental uncertainties on A, ¹⁹Ne provides the best sensitivity to right-handed currents among all mirror transitions. Other interesting cases are e.g. ¹³N and ¹⁷F, for which a 0.5% relative accuracy on A renders the result sensitive to a right-handed boson mass m₂ of about 300 GeV/c² (at 90% CL) assuming ζ = 0. This is similar to the present combined lower limit from all experiments in nuclear β-decay [121]. Note that for the nuclei mentioned here, a relative accuracy of 0.5% on A requires absolute precisions ranging from 0.5% (for ¹⁷F) to 2 × 10⁻⁴ (for ¹⁹Ne) [40].

The ν-asymmetry parameter, B, is also sensitive to right-handed charged weak currents [3]. Determining B requires, however, the recoiling nucleus to be observed in order to get access to the kinematics of the neutrino. The most precise result for this parameter in a nuclear decay has been obtained with ³⁷K nuclei trapped in the TRINAT MOT setup at TRIUMF [125]. The result, B = −0.755(20)_stat(13)_syst, is consistent with the SM value, B_SM = −0.7692(15), and provides a lower limit on the mass of the W₂ boson of m₂ > 180 GeV/c² (90% CL). Although this is not yet competitive with results from other measurements, the limitations could be overcome by improving statistics as well as the precision with which the degree of nuclear polarization of the atom cloud can be determined. An improved measurement of this parameter with polarized ³⁷K is currently being prepared at TRIUMF [104].

Measurements of the β particle longitudinal polarization are potentially very sensitive to right-handed parameters. Moreover, measurements with unpolarized nuclei are sensitive to the product of parameters, δζ, whereas measurements with polarized nuclei—the so-called polarization-asymmetry correlation [126]—are sensitive to their sum, δ + ζ, thus providing complementary constraints.

5.4.1. Longitudinal β particle polarization from unpolarized nuclei.

Relative β particle longitudinal polarization measurements with polarized nuclei are sensitive to (δ + ζ)², and are therefore sensitive to the mass of a right-handed W₂ boson, even when ζ ≈ 0 (section 5.1). Under specific experimental conditions such measurements can display enhanced sensitivities to deviations from maximal parity violation [135]. Two such experiments have been performed, one with ¹⁰⁷In polarized at mK temperatures and in a high internal hyperfine magnetic field [136], and the other with ¹²N polarized in a proton-induced polarization-transfer reaction on ¹²C [121, 137]. In both cases, relative measurements were performed in order to reduce instrumental effects and time-resolved positronium hyperfine spectroscopy was used for the analysis of the longitudinal polarization. Both experiments were complementary in terms of effects arising from the degree of nuclear polarization and from counting rates. Combining the results of these experiments (but not including additional data obtained with ¹⁰⁷In and quoted as preliminary in [138]) yielded the limit on the mass of the right-handed boson m₂ > 310 GeV/c² (at 90% CL)[121]. This is so far the most stringent limit on the mass of a hypothetical right-handed boson obtained from measurements at low energies.

The sensitivity of relative polarization-asymmetry correlation measurements in mirror transitions has been analyzed in the framework of general left–right symmetric models and compared to those in the above mentioned pure Gamow–Teller transitions of ¹²N and ¹⁰⁷In in [135]. It followed that for degrees of nuclear polarization exceeding 80% and when measuring at the maximum of the β particle energy spectrum, the most sensitive cases are ³H, ¹¹C, ¹⁵O, ¹⁷F, ²¹Na, ²⁵Al, ³⁹Ca and ⁴¹Sc, as well as ¹²N and ¹⁰⁷In, with sensitivities to m₂ ranging from about 500 GeV/c² up to 1.7 TeV/ c² for nuclear polarizations close to 100%. It was pointed out [2] that any measurement reaching the level of 500 GeV/c² for a W_R boson would be valuable. It is to be noted, however, that the effective sensitivity of such experiments depends strongly on the actual experimental conditions. Nevertheless, using thin implantation targets for the polarized nuclei, and high production yields, like those that will be available at new radioactive beam facilities such as FRIB [139], SPIRAL2/DESIR [140], HIE-ISOLDE [141] and SLOWRI (RIKEN) [142], would enable to reach new levels of sensitivity. An experiment with polarized ²¹Na, based on a compact positron polarimeter and with several other improvements with respect to the previous measurements, is currently under study at NSCL-MSU [143]. Performing a similar experiment, with the same setup, with the mirror isotope ²³Mg is further being considered in order to reduce systematic effects.

The D triple correlation, which drives the term J·(p_e × p_ν)/E_eE_ν in equation (3), is sensitive to an imaginary phase between the V and A couplings. It requires the use of mixed Fermi/Gamow–Teller transitions and the determination of the neutrino momentum through observation of the recoil ion.

In nuclear β-decay the D coefficient has only been measured in ¹⁹Ne decay. An overview of all four experiments performed is given in [145], the combined result being D = 0.0001 ± 0.0006. Even more precise values for the D coefficient have recently been obtained in neutron decay by the emiT [146, 147] and TRINE [148] experiments, leading to the combined result D_n = −0.000 12(20) [1]. A new measurement, with a ²¹Na sample, using a double-MOT setup and a reaction microscope to detect the recoil ions, is currently being prepared at KVI-Groningen [44]. A measurement of this parameter with ²³Mg is also being considered at GANIL [149].

The R correlation, which drives the term σ·(J × p_e)/E_e in equation (4), is sensitive to a phase between an exotic coupling (S,T) and a SM one (V,A), probing time reversal violating S and/or T couplings. It requires the transverse polarization of the β particle to be determined and this has been done so far by Mott scattering.

The first measurement of this correlation in nuclear β-decay was performed with ¹⁹Ne [150], yielding R = 0.079(53), and was statistics limited. Later, very precise measurements of the R coefficient have been carried out with ⁸Li [80], resulting in the final result R = (0.9 ± 2.2) × 10⁻³. A Japanese–Canadian collaboration is presently performing new measurements of R in ⁸Li decay [151] at ISAC-TRIUMF, using collinear laser optical pumping to polarize the Li nuclei and Mott scattering to analyze the transverse electron polarization, along with planar wire chambers for tracking the scattered electrons. The goal is to reach the level of final state interactions which are at the 10⁻⁴ level for this decay [80, 152].

Note finally that the very first measurement of R in neutron decay was reported recently [153, 154], yielding R = 0.004 ± 0.012_stat ± 0.005_syst. This result allowed a significant improvement in constraining scalar-type weak interaction couplings and related parameters in SM extensions with leptoquark exchange [2], as well as in the minimal supersymmetric standard model with R-parity violation [155], beyond the limits from all previous measurements [154].

A third, but not more easily accessible, $\mathcal {T}$-odd observable in nuclear β-decay is the five-fold angular correlation coefficient, noted E₁ [144], which drives the term J·(p_e × k)(J·k) with k the photon momentum vector. As J appears twice in this vector formula this correlation is proportional to the nuclear alignment. It can be investigated in βγ angular correlations with oriented nuclei. Although this coefficient, like the D coefficient, is also sensitive to a time reversal-violating phase, ϕ, between V and A couplings, it is complementary to D since it is ${\cal P}$-odd. To lowest order the coefficient E₁ that characterizes the size of the time-reversal violating effect can be written as E₁ = 2y sin ϕ/(1 + y²), with ye^iϕ ≡ 1/ρ the Fermi/Gamow–Teller mixing ratio [156]. A more complete expression, including recoil corrections and final state electromagnetic corrections was given in [144].

This correlation has been addressed only once, with ⁵⁶Co [156], yielding E₁ = −0.011(22) corresponding to ϕ = (183 ± 6)°. Currently an experiment with ³⁶K, which is considered a potentially sensitive candidate for such a measurement [157], is being prepared [158] at the BECOLA low-energy beam line that is under construction at NSCL-MSU [159].

The largest of the induced weak currents discussed above is the weak magnetism which leads to the second term in equation (28) for the vector hadronic current in the β-decay of a nucleon. This was generalized to nuclear β-decays by Holstein [20], who encoded the nuclear structure aspects of the problem into ten so-called induced form factors denoted a,b,c,d,e,f,g,h,j₂ and j₃. These are in principle accessible experimentally and can, with the impulse approximation, be expressed in terms of coupling constants C_V  = V_ud G_F g_V (q² → 0), C_A = V_ud G_F g_A(q² → 0), f_M(q² → 0), etc and nuclear matrix elements. For β transitions between analogue states the CVC hypothesis allows the extraction of the weak magnetism form factor, b, from the magnetic moments of the mother and daughter isotopes [185]. Superallowed Fermi transitions and mirror transitions are therefore ideally suited to study fundamental properties of the weak interaction with minimal disturbance of the effects of induced weak currents. For retarded β transitions, such as the decay of ⁶⁰Co (log ft = 7.5), other induced terms play a dominant role [79].

Recently a survey and analysis was made of existing data on the effects of these induced weak currents [22]. This will help the interpretation of upcoming correlations measurements reaching precisions of the order of 10⁻³ in terms of new physics.

In order to study weak magnetism in more detail, for transitions between non-analogue states, the new and compact β spectrometer (miniBETA) that is currently being developed by the universities of Krakow and Leuven (section 4.2.2) will be used as well. Precision measurements of the shape of β particle spectra for transitions with relatively high endpoint energies will give direct access to the weak magnetism, with minimal disturbance from other induced form factors or from the Fierz interference term.

Important improvements in precision for β-asymmetry measurements in nuclear β-decay (section 4.2.2) can be achieved if atoms and ions in traps can be polarized. This would, in addition, allow performing also particle trap-based investigations of other correlations in β-decay involving the nuclear spin. It thus represents one potential future direction, but also one of the important challenges for the field.

Ions stored in Paul traps could be polarized in situ by using the laser optical pumping technique. Polarizing ions in Penning traps would be more complicated since here the nuclear and electronic spins are usually decoupled due to the strong magnetic field so that in situ optical pumping cannot be applied. The ions would then have to be polarized in beam in a collinear geometry prior to injecting them into the trap.

For MOTs, optical pumping of the trapped atom cloud has successfully been applied for ³⁷K [125] and ⁸⁰Rb [113] already. To determine the degree of polarization, photoionization from excited states is used, with absolute precisions for the nuclear polarization as good as 0.5% having been achieved already [125]. This method is, however, far from easy and needs further optimization in order to reach the precision level of about 0.1% that will be required in order for the polarization not to limit the sensitivity to non-standard model physics.