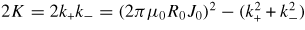On the conditions for up–down asymmetry in the core of tokamak equilibria: a matter of simple geometry

A couple of interesting theoretical results have recently been reported with the aim of understanding how to enforce up–down asymmetry (UDA) in the core of a tokamak plasma [1, 2], a possible means to induce intrinsic rotation via symmetry breaking along magnetic-field lines [3–6]. The Grad–Shafranov (GS) equation has been expanded and analytically solved near the magnetic axis to conclude that flux surfaces there are, in general, ellipses [1, 2]¹:

$$\begin{eqnarray} &&\fl(2/\pi \mu_{0} R_{0})\psi(x,y)\approx (J_{0}+ \varepsilon^{2}C_{0})x^{2} - 2\varepsilon^{2}S_{0}xy\nonumber\\ &&+\,(J_{0}- \varepsilon^{2}C_{0})y^{2} , \end{eqnarray} \tag{ 1 }$$

where μ₀ is the vacuum magnetic permeability, ψ represents the flux of the poloidal magnetic field, x and y are Cartesian coordinates on a poloidal cross-section, measured from the magnetic axis of the tokamak (located at R₀), ε is the inverse aspect ratio, J₀ is the plasma current density on axis and C₀ and S₀ are shaping coefficients set, to a large extent, by external conditions². These ellipses are tilted by an angle φ (between their semi-major axes and the tokamak vertical axis, and measured clockwise from the latter) and have an elongation κ (with 1 ⩽ κ < ∞) according to

$$\begin{eqnarray} &\tan(2\varphi)=S_{0}/C_{0}, \nonumber\\ &(\kappa^{2}-1)/(\kappa^{2}+1)=\varepsilon^{2}(C_{0}^{2}+S_{0}^{2})^{1/2} /J_{0}, \end{eqnarray} \tag{ 2 }$$

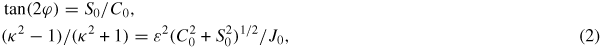
being assumed here that |φ| ⩽ π/4, as in standard tokamak equilibria. That tilting and elongation are obvious necessary conditions for UDA can hardly come as a surprise, but the key role that a reduced J₀ may play in increasing the latter has been put forward by (2), whereas a figure of merit to quantify UDA has also been introduced which, in the case of the elliptical quadratic form (1), becomes [1, 2]³

$$\begin{equation} \eta_{0}=\varepsilon^{2}|S_{0}| / \pi[J_{0}^{2}-\varepsilon^{4}(C_{0}^{2}+S_{0}^{2})]^{1/2} \approx \varepsilon^{2}|S_{0}|/\pi J_{0}, \end{equation} \tag{ 3 }$$

or, accounting for (2),

$$\begin{eqnarray} &&\fl\eta_{0}=|\sin(2 \varphi)| [(\kappa^{2}-1)/2\kappa] /\pi\approx |\sin(2 \varphi)| (\kappa-1)/\pi, \end{eqnarray} \tag{ 4 }$$

the approximations in (3) and (4) being valid when $\varepsilon^{2}(C_{0}^{2}+S_{0}^{2})^{1/2} \ll J_{0}$ and, therefore, when κ ≈ 1. Equation (3), which reads as a main result, states that core asymmetry is basically controlled by the ratio between the odd shaping coefficient S₀ and the current density on axis J₀. Moreover, in order not to deplete too much the total plasma current when pushing J₀ down, which is the case with monotonic current-density profiles, the use of hollow current-density equilibria (hence with reversed magnetic shear) has been advocated, having furthermore been shown that the latter do enhance UDA penetration to the core [1, 2].

The purpose of this paper is essentially threefold: to rederive the 1/J₀ scaling for on-axis UDA drawing directly from long-established results [7, 8] and using basic geometry (in combination with unsophisticated, back-of-the-envelope calculations); to advance an alternative, eventually more appropriate figure of merit for measuring on-axis UDA; and to show that boosting on-axis UDA by forcing J₀ to go down will most likely reveal itself not to be a very useful endeavour, as the latter cannot be made arbitrarily small without dramatically changing the very nature of the equilibrium (turning the elliptical O-point at the magnetic axis into a hyperbolic X-point) [9]. Simply stated, the basic problem to address is how to confine a given amount of current I, or flux ψ, in a central plasma channel around the magnetic axis in such a way as to ensure maximum UDA. The answer to this question can be straightforwardly and easily built based upon three well-known facts: that nested flux surfaces in a tokamak become ellipses in the neighbourhood of its magnetic axis [8], that for a given label the area of a flux surface with elliptical cross-section increases with elongation and that the current density is lower the larger the cross-sectional area where a same current is to be distributed. Therefore, going for stronger UDA (hence larger κ) in a tokamak core implies going simultaneously for weaker J₀. Besides the inherent pedagogical interest there is in rederiving (1)–(4) above following a more down-to-earth approach, such results should be scrutinized to see if they can indeed deliver what they promise: to improve plasma confinement by enhancing intrinsic rotation in the tokamak core via an increase of on-axis UDA. The quest for effective mechanisms capable of generating substantial amounts of intrinsic (or spontaneous) rotation in tokamaks is one of the current key challenges in fusion research, particularly in view of future reactor-grade machines such as ITER (where external torque is expected to be small), so it is never too much to emphasize the importance of the subject and the need to properly gauge each of the various proposals aiming at increasing toroidal momentum transport by breaking the symmetry (or parity) along the magnetic field [5, 6, 10, 11]. In fact, UDA is only one of the contributions to the so-called residual stress (others stemming from E × B shearing and from higher order terms in normalized Larmor radius), which provides a seed rotation that can be convected by the pinch terms in the toroidal momentum balance equation (proportional to rotation and arising from the Coriolis effect and the particle flux) and can thus sustain a rotation gradient (by balancing the diagonal term proportional to the latter) in the absence of an external torque [3–6, 11]. Hence, and although decreasing J₀ does lead to a growth of on-axis UDA, it will be shown below that such a route to get enhanced intrinsic rotation will probably be ineffective as it will be seriously hindered by the fact that 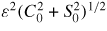$\varepsilon^{2}(C_{0}^{2}+S_{0}^{2})^{1/2}$ acts as a lower bound for J₀. In other words, the stronger the ellipticity one tries to impose by external means (using, for instance, shaping coils), the higher the smallest current density allowed on axis and, inversely, the lower this current density becomes, the weaker the shaping must be. There is, therefore, a structural, topological limit preventing J₀ from becoming as small as it may be desirable or needed to ensure a given level of UDA, which is in fact linked to a recently demonstrated theorem on magnetostatic fields in axisymmetric plasmas [9].

That tokamak flux surfaces near the magnetic axis are ellipses is a fact which has actually been known and established for quite a long while now, either implicitly for more than forty years, via expansions about that point [7], or explicitly for more than thirty, in analytical solutions to the GS equation in its vicinity [8]. Besides, for standard tokamak equilibria with nested flux surfaces (hence without current reversal [12–14]), it is trivial to conclude that to lowest order around the magnetic axis the latter cannot but have elliptical shape, simply because ψ has an extremum there, so⁴

$$\begin{equation} \rho^{2}(x,y)\approx x^{2}+y^{2}/\kappa^{2}, \end{equation} \tag{ 5 }$$

where ρ is the flux-surface label, coincident here with its semi-minor axis [8]. Two other results can also be imported directly from the classical literature on magnetic confinement [8], which read⁵

$$\begin{equation} \psi(\rho) \approx \pi\mu_{0} R_{0} J_{0} [\kappa^{2}/(\kappa^{2}+1)]\rho^{2} \end{equation} \tag{ 6 }$$

and

$$\begin{equation} I(\rho) \approx (1 /\mu_{0} R_{0} ) [(\kappa^{2}+1)/2\kappa ] \rho \psi'(\rho) . \end{equation} \tag{ 7 }$$

It is worth mentioning that, whereas (5) has been written for an up–down symmetric equilibrium [8], (6) and (7) are quite general and thus valid for tokamak equilibria with UDA because they are laid down entirely in terms of quantities that are flux functions.

As already stated, both tilting and elongation are key ingredients needed for UDA so, regarding the former, the first thing to do is to rotate the ellipse (5) by the tilting angle φ, which amounts to replace x and y in this equation by x cos(φ) − y sin(φ) and x sin(φ) + y cos(φ), respectively, whence

$$\begin{eqnarray} &&\fl [2\kappa^{2}/ (\kappa^{2}+1)]\rho^{2}\approx [1+\cos(2\varphi)(\kappa^{2}-1)/(\kappa^{2}+1)]x^{2}\nonumber\\ &&-\,2[\sin(2\varphi)(\kappa^{2}-1)/ (\kappa^{2}+1)]xy \nonumber\\ &&+\,[1-\cos(2\varphi)(\kappa^{2}-1)/(\kappa^{2}+1)]y^{2}. \end{eqnarray} \tag{ 8 }$$

As for shaping, it suffices to recall that, starting from a circular current-carrying channel with radius ρ and proceeding to fashion it into an elliptical form (whilst keeping ρ as the semi-minor axis), its cross-sectional area A increases with elongation according to πκρ² and also that, since around the magnetic axis the current density is essentially constant and equal to J₀, the current carried I is simply J₀A, so

$$\begin{equation} I(\rho)\approx J_{0}A(\rho) = \pi J_{0} \kappa \rho^{2} . \end{equation} \tag{ 9 }$$

Equation (9), which is also an immediate consequence of (6) and (7), tells a very simple story and, in essence, the whole story there is about the 1/J₀ scaling for on-axis UDA in tokamaks: when confining a given current I within a channel of width ρ around the magnetic axis, a stronger elongation κ implies a smaller current density J₀ (to keep constant the product J₀κ)⁶. It is worth noting that a similar reasoning can be conducted at constant flux ψ, instead of constant current I, since κ²/(κ² + 1) increases monotonically with κ and so (6) shows once more that stronger ellipticity requires lower J₀.

It is now time to go from geometry to physics and relate the geometrical parameters in curve (8) with physical quantities and, to do so, it is convenient to simplify its writing by introducing the dimensionless shaping, or asymmetry-controlling, parameters

$$\begin{eqnarray} &c_{0}\equiv \cos(2\varphi)(\kappa^{2}-1)/(\kappa^{2}+1), \nonumber\\ &s_{0}\equiv\sin(2\varphi)(\kappa^{2}-1)/(\kappa^{2}+1), \end{eqnarray} \tag{ 10 }$$

which can be inverted to give

$$\begin{eqnarray} &\tan(2\varphi) = s_{0}/c_{0}, \nonumber\\ &(\kappa^{2}-1)/(\kappa^{2}+1)=(c_{0}^{2} + s_{0}^{2})^{1/2}, \end{eqnarray} \tag{ 11 }$$

and by subsequently combining (6), (8) and (10) to yield

$$\begin{eqnarray} &&\fl(2/\pi \mu_{0} R_{0})\psi(x,y)\approx J_{0} [(1+c_{0})x^{2} - 2s_{0}xy + (1-c_{0})y^{2} ],\nonumber\\ \end{eqnarray} \tag{ 12 }$$

so that (11) and (12) are the same as (1) and (2), with

$$\begin{eqnarray} &c_{0}= \varepsilon^{2}C_{0}/J_{0}, \nonumber\\ &s_{0}= \varepsilon^{2}S_{0}/J_{0} . \end{eqnarray} \tag{ 13 }$$

Note there is actually no need for ε to appear explicitly in the present problem, which is quite easy to understand from the physics point of view: very close to the magnetic axis toroidicity plays essentially no role, so ε can simply be scaled out of the theory (for instance, be absorbed in some coefficients' definition), the physics being clearly dominated by the limit ρ ≈ 0 rather than by the condition ε ≪ 1^7,8. To impart additional physical meaning to c₀ and s₀ it is useful, with the help of (11), to rewrite (6) as

$$\begin{equation} \psi(\rho) \approx (\pi/2)\mu_{0} R_{0} J_{0} [1+(c_{0}^{2}+s_{0}^{2})^{1/2}] \rho^{2}, \end{equation} \tag{ 14 }$$

allowing 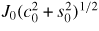$J_{0} (c_{0}^{2}+s_{0}^{2})^{1/2}$ to be interpreted as a virtual, pseudo-current density J_p0 that represents the value by which the current density $J_{0} [1+(c_{0}^{2}+s_{0}^{2})^{1/2}]$ that would flow within a circular flux surface with radius ρ and encircling the flux ψ must be depleted so as to have its cross-section shaped into an ellipse with elongation κ given by (11). Putting then

$$\begin{equation} J_{\rm{p}0}\equiv J_{0} (c_{0}^{2}+s_{0}^{2})^{1/2} \end{equation} \tag{ 15 }$$

to rewrite (14) as

$$\begin{equation} \psi(\rho) \approx (\pi/2)\mu_{0} R_{0} (J_{0}+J_{\rm{p}0}) \rho^{2}, \end{equation} \tag{ 16 }$$

the physical mechanism behind on-axis UDA can thus be seen as a competition between the actual current density J₀ flowing on the magnetic axis and the shaping pseudo-current density J_p0 imposed mainly by external means, the smaller the latter (and, consequently, the larger the former) the closer the flux surface labelled by ρ becomes to a circumference. Moreover, looking again at (11) and accounting for (15), it becomes evident that the ratio between these two current densities is bounded according to 0 ⩽ J_p0/J₀ < 1, which means it provides an appropriate way to quantify, or measure, the ellipticity of the flux surfaces around the magnetic axis, an issue to be discussed in detail below. The current-density analogy can be pushed even further by writing J_p0 in (15) in terms of even and odd shaping pseudo-current densities according to

$$\begin{eqnarray} &J_{\rm{p}0} =(J^{2}_{{\rm c}0}+J^{2}_{{\rm s}0})^{1/2}, \nonumber\\ &J_{{\rm c}0} \equiv J_{0}c_{0},\nonumber\\ &J_{{\rm s}0} \equiv J_{0}s_{0}, \end{eqnarray} \tag{ 17 }$$

so (12) becomes

$$\begin{eqnarray} &&\fl(2/\pi \mu_{0} R_{0})\psi(x,y)\approx (J_{0}+J_{{\rm c}0})x^{2} - 2J_{{\rm s}0}xy + (J_{0}-J_{{\rm c}0})y^{2},\nonumber\\ \end{eqnarray} \tag{ 18 }$$

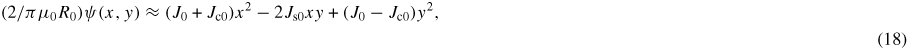
where (apart from the needless, and eventually misleading, ε² factor) J_c0 and J_s0 are no other than the C₀ and S₀ coefficients, respectively, as seen by confronting (13) with (17), or (1) with (18).

Despite a certain pictorial, visual appeal it may have [1] ⁹, the quantitative definition of UDA that leads to (3) has nonetheless two shortcomings: not only it yields a figure of merit with no proper upper bound (η₀ diverging with κ when κ ≫ 1 and thus failing to give a natural maximum value for UDA), but the main result of the theory, the 1/J₀ scaling in (3) for on-axis UDA, emerges not as a general property but as an approximation instead (and one that appears, furthermore, to be valid only in the limit of reduced elongation, whereas strong elongation is precisely the ultimate goal here). Since the elliptical form is a universal feature of flux surfaces nested around, and close to, the magnetic axis, an alternative measure for UDA can be sought by inspecting (1), (8), (12) or (18) to conclude on-axis UDA is present if, and only if, the coefficient of the xy term in these equations does not vanish, which suggests its strength may provide a proper means to quantify UDA. However, to produce a figure of merit for UDA, this coefficient must still be gauged against those multiplying x² and y² in (1), (8), (12) or (18), which can be done, for instance, dividing the former by the sum of the latter, whence the definition

$$\begin{eqnarray} &&\fl\eta_{\rm{UDA}}\equiv\sin(2\varphi)(\kappa^{2}-1)/ (\kappa^{2}+1)=s_{0}=\varepsilon^{2}S_{0}/J_{0}=J_{{\rm s}0}/J_{0}. \nonumber\\ \end{eqnarray} \tag{ 19 }$$

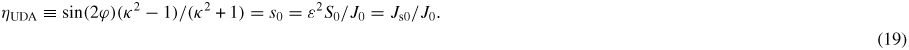
Not only it is immediate to check that 0 ⩽ |η_UDA| < 1 (a negative sign indicating simply that flux surfaces are tilted anti-clockwise with respect to the tokamak vertical axis), so (19) brings forth a natural measure and a bounded scale to quantify UDA between zero and unity, but also UDA's inverse law with J₀ appears as a universal behaviour, independently of any smallness criterion either on the inverse aspect ratio or on the shaping coefficients, as happens with η₀ in (3)¹⁰. In addition, η_UDA in (19) clearly shows that there is UDA if, and only if, tilting and elongation are both present (that is, if and only if φ ≠ 0 and κ ≠ 1 apply simultaneously), being even possible to write η_UDA as the product of two figures of merit, defined one for tilting and one for ellipticity:

$$\begin{eqnarray} &&\fl \eta_{\rm{UDA}}=\eta_{\rm{t}}\eta_{\rm{e}} , \nonumber\\ &&\fl \eta_{\rm{t}}\equiv \sin(2\varphi)=s_{0}/(c_{0}^{2}+s_{0}^{2})^{1/2}\!=S_{0}/(C_{0}^{2}+S_{0}^{2})^{1/2}\!=J_{{\rm s}0}/J_{{\rm p}0}, \nonumber\\ &&\fl \eta_{\rm{e}}\equiv(\kappa^{2}-1)/ (\kappa^{2}+1)=(c_{0}^{2} +s_{0}^{2})^{1/2}\nonumber\\ &&=\varepsilon^{2}(C_{0}^{2}+S_{0}^{2})^{1/2} /J_{0} = J_{{\rm p}0}/J_{0}, \end{eqnarray} \tag{ 20 }$$

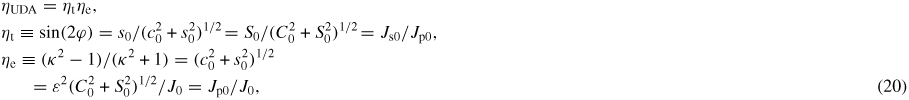
where (2), (11), (13), (15) and (17) may be of use and with, quite naturally, −1 ⩽ η_t ⩽ +1 and 0 ⩽ η_e < 1. Still a further advantage of the η_UDA definition in (19) or (20) is to make clear that maximum UDA (that is, |η_UDA| = 1) occurs necessarily, and simultaneously, for φ = ±π/4 and κ ≫ 1 (or c₀ = 0 and |s₀| ≈ 1), a feature that is quite evident but does not follow from the definition of η₀ in (3) or (4), which may always become arbitrarily large with κ (when $J_{0}\approx J_{{\rm p}0}=\varepsilon^{2}(S_{0}^{2}+C_{0}^{2})^{1/2})$ as long as φ does not strictly vanish.

In essence, aiming at making UDA eventually easier to grasp and understand and also to put things into perspective with respect to the classical literature on tokamak equilibrium [7, 8], one has revisited hereabove results that have been reported showing that to boost on-axis UDA one may either increase the elongation of flux surfaces acting from the outside or reduce the current density flowing in the tokamak core (or do both) [1, 2]. There is, however, a condition that must not be overlooked and which is already plainly obvious by simple inspection of equations (2) or (3) and which imposes a structural bound on how small can J₀ be made: in fact, for the quadratic forms in equations (1), (12) or (18) to describe ellipses it is necessary, respectively, that

$$\begin{eqnarray} &1 > c_{0}^{2} + s_{0}^{2},\nonumber\\ &J_{0}> \varepsilon^{2}(C_{0}^{2} + S_{0}^{2})^{1/2}, \nonumber\\ &J_{0} > (J^{2}_{{\rm c}0}+J^{2}_{{\rm s}0})^{1/2} =J_{{\rm p}0} , \end{eqnarray} \tag{ 21 }$$

where (17) has also been used. Conditions (21), which are once more of a geometrical nature¹¹, have been shown to be inherently linked to the structure of axisymmetric magnetic topologies (not necessarily of equilibrium) with nested flux surfaces, the inversion of the inequalities in (21) inducing a modification in the structure of the equilibrium by changing the O-point at the magnetic axis into an X-point [9]. Indeed, (21) can be restated in terms of the so-called Gaussian curvature of the poloidal magnetic field's flux (the determinant of its second-derivatives', or Hessian, matrix)

$$\begin{equation} K=(\partial^{2}\psi/\partial x^{2})(\partial^{2}\psi/\partial y^{2})-(\partial^{2}\psi/\partial x \partial y)^{2}, \end{equation} \tag{ 22 }$$

which, recalling (1), (12) or (17) and (18), can take the forms

$$\begin{eqnarray} &&\fl K/(\pi \mu_{0}R_{0})^{2}=J_{0}^{2}[1-(c_{0}^{2}+s_{0}^{2})]=J_{0}^{2}-\varepsilon^{4}(C_{0}^{2}+S_{0}^{2})\nonumber\\ &&=J_{0}^{2}-J^{2}_{{\rm p}0}, \end{eqnarray} \tag{ 23 }$$

the sign of K determining how flux surfaces arrange themselves around the magnetic axis (where the poloidal magnetic field vanishes): nested ellipses when K > 0, as in (21), or non-nested hyperbolas when K < 0 [9]¹². The physical mechanism governing on-axis UDA (that of a competition between J₀ and J_p0) turns out to be the same mechanism establishing the magnetic axis' topology via the competition between external shaping fields, which drive J_p0 and push for a hyperbolic configuration, and the field created by the local plasma current density J₀ which, as long as the constraints in (21) are verified, ensures the elliptical layout characteristic of standard tokamak equilibria [9]. Putting it simply, inequalities (21) make one wonders if the attempts to enforce on-axis UDA via depletion of the core plasma current density are indeed an effective means to get increased intrinsic rotation, as they imply that c₀ and s₀ (C₀ and S₀ if measured in units of current density) or, equivalently, J_c0 and J_s0 cannot be made arbitrarily large while simultaneously making J₀ smaller and smaller to increase UDA's figure of merit η_UDA defined in (19) or (20). In fact, (21) imposes an interplay between J₀ and J_p0 that makes them bound each other in a manner as to ultimately pull the system away from a required state of increased on-axis UDA. For instance, to approach maximum UDA one must then follow a path, after combining (19) and (21) with J_c0 = 0, such that J₀ ≈ |J_s0| while having, at the same time, J₀ > |J_s0|, which imposes such a strong coupling between J₀ and J_s0 = ε²S₀ that it will be very hard, if not downright impossible, to implement and maintain it in an actual tokamak experiment. This will be so much so inasmuch as J₀ and S₀ may be regarded as independent parameters defining the equilibrium shape, since the former is a property of the core whereas the latter depends strongly on the external field [2]. The practical difficulty of tuning an experiment along such a path is a hint to the fact that one is entering the realm of current-hole scenarios [9], a real possibility to be accounted for in the quest for strong on-axis UDA if J₀ is pushed to very low values using hollow current-density profiles.

It is still interesting to adopt an engineering point of view and carry out the exercise of sketching how an experiment on on-axis UDA could be designed and see, in particular, how the strong constraint imposed by (21) would eventually come into play. Hence, given a certain amount of current I to be confined within a central plasma channel of width ρ around the magnetic axis and with prescribed tilting η_t and ellipticity η_e, there are three parameters to fix, which define the experimental conditions: the on-axis current density J₀ and the pair of shaping pseudo-current densities J_c0 and J_s0 (or, equivalently, any of the pairs of shaping coefficients c₀ and s₀ or C₀ and S₀). To do so, conditions (9) and (20) can be used to get

$$\begin{equation} J_{0} \approx J_{{\rm o}0} [(1-\eta_{\rm e})/(1+\eta_{\rm e})]^{1/2} \end{equation} \tag{ 24 }$$

and

$$\begin{eqnarray} &J_{{\rm c}0} \approx J_{{\rm o}0} (1-\eta_{\rm t})^{1/2} \eta_{\rm e} [(1-\eta_{\rm e})/(1+\eta_{\rm e})]^{1/2}, \nonumber\\ &J_{{\rm s}0} \approx J_{{\rm o}0} \eta_{\rm t} \eta_{\rm e} [(1-\eta_{\rm e})/(1+\eta_{\rm e})]^{1/2} , \end{eqnarray} \tag{ 25 }$$

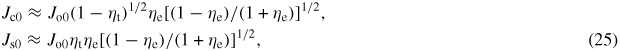
where, from (9),

$$\begin{equation} J_{{\rm o}0} \equiv I/\pi \rho^{2} = J_{0} \kappa \end{equation} \tag{ 26 }$$

can be interpreted as, say, a reference current density, more precisely, that which would flow in the vicinity of the magnetic axis if flux surfaces were circular (with elongation κ = 1)¹³. In going for increased η_UDA, and looking at (20), (24) and (25), one can put η_t = 1 (so J_c0 = 0 and the external drive goes entirely to the odd component J_s0) while also making η_e ≈ 1 (so κ ≫ 1), which leads not only to J₀ ≈ 0 but to J_s0 ≈ 0 as well, the former reading as a most natural consequence of (9), or of its equivalent (26), when κ ≫ 1, the latter as the most surprising conclusion that pushing for enhanced on-axis UDA ends up by virtually killing it. The reason for this apparent paradox lies precisely with inequality (21) or, going back a little further, with (2), (11) or (20), which all show that, since (κ² − 1)/(κ² + 1) ⩽ 1 (because, by definition, κ ⩾ 1), their right-hand side can never go above one so, when reducing J₀ to increase ellipticity (and thence UDA), the externally controlled pseudo-current density J_s0 (or the equivalent shaping coefficients s₀ or S₀) must also be made smaller, along a path that ultimately leads to the vanishing of both J₀ and J_s0. The way around such a tightly constrained route, at least formally and following (24) and (25), is to ensure that J_s0/J₀ = η_t η_e ≈ 1 as both numerator and denominator approach zero but, as discussed in the previous paragraph, this would require the finest and most faultless of tunings to be applied simultaneously on two quantities (J₀ and J_s0) that determine the equilibrium in the tokamak core and are considered to be independent [2], making it a practically impossible task to be carried out in a real experiment. In terms of the Gaussian curvature K introduced in (22) and (23), forcing J₀ to approach zero without disrupting the elliptical, O-point structure of the equilibrium around the magnetic axis would imply following a path for which K ≈ 0 and, therefore, would seriously hinder one's ability to describe arbitrary configurations [9]¹⁴.

In the present paper, by simply referring to the classical, consecrated literature on tokamak equilibrium (which is more than three decades old [7, 8]) and by essentially using a single basic ingredient (namely, geometry), recent results have been rederived according to which UDA scales inversely with the on-axis current density [1, 2]. Indeed, as shown above, once tilting has been imposed by external coils and since nested flux surfaces must be, by obvious arguments, ellipses close and around the magnetic axis, such a scaling arises from the trivial facts that, at constant width (as measured by its semi-minor axis), the cross-sectional area of an ellipse increases with elongation and that, for a same current, the corresponding density is inversely proportional to the area over which it is distributed. A figure of merit has also been proposed to quantify on-axis UDA that is bounded between zero and unity and, furthermore, yields the UDA scaling with the inverse on-axis current density as a general law and not one which is valid in the case of weak ellipticity only [1, 2]. In addition, it has been demonstrated that the externally controlled shaping coefficients and the on-axis current density (the parameters that define on-axis UDA) bound each other in such a way as to eventually trigger a kind of negative feedback whereby increasing ellipticity will lead to a larger minimum current density in the core, whereas decreasing the latter will inhibit attainment of larger elongation, which is (together with tilting) one of the necessary ingredients for UDA. Hence the main conclusion in this paper, that the seemingly obvious approach to boost on-axis UDA in a tokamak by increasing the shaping coefficients whilst simultaneously and independently decreasing the central current density will most likely fail.

As for the use of hollow current-density profiles to enable lower current densities in the tokamak core and thus increase on-axis UDA (eventually leading to enhanced intrinsic rotation there and improved plasma confinement) [1, 2], one must be aware that forcing the plasma into strongly reversed shear configurations may lead to situations already within the current-hole domain, where equilibria may depart from the classical nested tokamak configuration [9, 12–14]. Moreover, relying on equilibria with strong magnetic-shear reversal would demand going for so-called advanced tokamak scenarios, these still lacking the robustness and reliability of the other modes of operation retained for ITER, which are the ELMy H-mode and hybrid scenarios and have, respectively, zero and weakly reversed shear in the inner half of the plasma [15–17]. Finally, note there is no issue here whatsoever about an UDA effect on intrinsic rotation, an effect that is well-understood theoretically and has been seen experimentally [3–6], but what is questioned in this paper is the possibility to make UDA penetrate effectively into the central part of a tokamak plasma (by decreasing the current density there), in order to significantly enhance core confinement. Ultimately, a definite answer on how large on-axis UDA must be to have a real impact on intrinsic rotation and confinement will only be provided by performing gyrokinetic calculations on equilibria spanning different values of core current density and UDA.

This work has been carried out under the European Fusion Development Agreement (EFDA), as well as within the framework of the Contract of Association between the European Atomic Energy Community and the Instituto Superior Técnico (IST), and it has also received financial support from the Fundação para a Ciência e a Tecnologia (FCT, Lisboa), namely through the contract of Laboratorio Associado, under project No. Pest-OE/SADG/LA0010/2013. The content of this paper is the sole responsibility of the authors and does not necessarily represent the views of the European Commission, of FCT, of IST, or of their services.