Suprathermal ion studies in ECRH and NBI phases of the TJ-II stellarator

In fusion plasmas, ions with velocities much larger than the characteristic local thermal (Maxwellian) velocity are known as fast ions, superthermal or suprathermal ions. They can be created by neutral-beam injection (NBI), radiofrequency wave heating, fusion reactions and other methods. Fast ions created in nuclear or atomic reactions have a well-defined initial energy (or birth energy), while fast ions generated by RF heating do not. Depending on the source, the energy of the fast ions varies from tens of kiloelectronvolts to several megaelectronvolts. There are many aspects in plasma physics for which the fast-ion distribution function is important (e.g. sawtooth stabilization, ion cyclotron resonance heating (ICRH), instabilities and additional heating mechanism of thermal ones) [1–4].

These fast ions execute orbits that are much larger than those of thermal particles; quantitatively, the fast-ion gyroradius ρ_f is much larger than the thermal ion or electron gyroradii: ρ_f ≫ ρ_i ≫ ρ_e. The speed v_f of fast ions is usually intermediate between the thermal electron and ion speeds, v_e ≫ v_f ≫ v_i. Because of the large excursions of their orbits and their high speeds, fast ions interact differently with the plasma and with electromagnetic fields than thermal particles do. A goal of fast-ion studies is to understand the effect of these interactions on the fast-ion distribution function f(x, v, t), with the variables representing position, velocity and time, and, in turn, to understand the effect of the fast-ion population upon the background plasma.

We have already reported the observation, by spectroscopic techniques of suprathermal protons in ECRH TJ-II plasmas [4] capable of contributing to the heating of the thermal component. These results have been used to support theories based on parametric decay mode conversion in ECRH plasmas with much lower threshold than expected [5]. In addition, former experiments performed in TJ-II have also initiated the study (detection and behaviour) of the suprathermal component in heavier ions by the spectroscopic method [6], by extending the integration times to get good photon statistics. More recently we have added to passive spectroscopic techniques a luminescent probe (LP) [7] to detect those suprathermal ions escaping from the confinement region, in both cases with time resolution and with additional spatial resolution in the first case. The excellent sensitivity and operation of the LP in a height pulse analysis regime, and data processed by an ad hoc digital pulse algorithm, has enabled the determination of the ion distribution function in ECRH and NBI regimes [8]. In this work we exploit these two complementary approaches to extract information on the suprathermal ion confinement and about their spatial and time properties evolution using specific TJ-II scenarios and selected discharges within them.

The paper is organized as follows. First, we will explain briefly the experimental techniques used in this work and typical results obtained in TJ-II scenarios. Second, we will present the most relevant results obtained with data provided by the LP. Third, we will present selected results of the suprathermal behaviour of protons and impurities inside the plasma obtained by passive emission spectroscopy. Finally, conclusions are drawn.

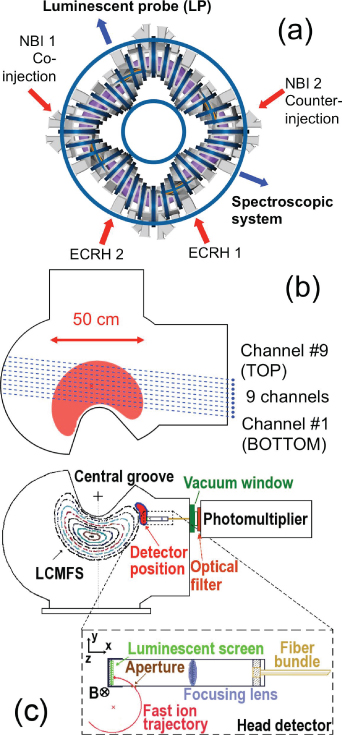
The TJ-II is a four-period, low magnetic shear stellarator with major and averaged minor radii of 1.5 m and ⩽0.22 m, respectively. It is designed to explore a wide rotational transform range (0.9 ⩽ ι(0)/2π ⩽ 2.2) in low, negative shear configurations (dι/ι < 6%). Its magnetic field is generated by a system of poloidal, toroidal and vertical field coils. These include 32 toroidal field (TF) coils whose centres follow a toroidal helix of major radius 1.5 m, minor radius 0.28 m and pitch law θ = −4φ (where θ and φ are the poloidal and toroidal angles). The coil system is completed by a central conductor made up of two coils: a purely horizontal one of 3 m diameter and a helical winding wrapped around this coil that follows the same winding law as the TF coils. The resultant plasma cross-section is bean shaped with magnetic field B(0) ⩽ 1 T. Plasmas created with hydrogen are heated using two gyrotrons operated at 53.2 GHz, the second harmonic of the electron cyclotron resonance frequency (P_ECRH ⩽ 600 kW, t_discharge ⩽ 300 ms) and central electron densities, n_e(0), and temperatures, T_e(0), up to 1.7 × 10¹⁹ m⁻³ and 1 keV, respectively, are achieved in ECRH plasmas. The NBI system at TJ-II consists of two tangential injectors in the co-counter configuration: NBI 1 and NBI 2, parallel and anti-parallel to the magnetic field (up to 700 kW from each) with typical duration of 100 ms. The TJ-II neutral beams are composed of H atoms with energies 30, 15 and 10 keV (per cent proportion: 55 : 25 : 20) [9], having a 1/e divergence of 1.3° and a total current of 50 A. Typical central electron densities, n_e(0), and temperatures, T_e(0), in NBI discharges are up to 5 × 10¹⁹ m⁻³ and 0.3 keV, respectively. A general view of the TJ-II device with the toroidal position of the suprathermal diagnostics used in this work, with respect to the main TJ-II heating systems, is shown in figure 1(a).

Zoom In Zoom Out Reset image size

The two TJ-II phases, ECRH and NBI, are almost completely independent, which permits the number and energies of suprathermal ions observed separately in both phases to be studied separately. During the NBI phase the gyrotrons are turned off, except for a few milliseconds of overlapping in order to have a target plasma from which the pure NBI phase starts. This is carried out to avoid the possible damage on the gyrotrons due by the microwave power reflected when in the NBI phase the plasma density exceeds the ECRH cut-off density. Therefore, the suprathermal ions detected in the ECRH phase are due exclusively to the microwave heating without any influence from NBI. The assumption is that parametric decay instabilities might be its cause as supported by Gusakov et al [5].

Previous works [10, 11] carried out in the TJ-II stellarator have presented a technique for measuring the thermal and suprathermal ion temperatures using high-resolution Doppler spectroscopy. The thermal proton temperatures obtained using this method agree reasonably well with the thermal temperatures obtained with a neutral particle analyser (NPA) [12]. The spectral method involves detecting and analysing the wavelength displacement of H_α emission, which indicates how fast the emitting neutral is moving along the line-of-sight. Low energy neutrals, which are collisionally in thermal equilibrium with protons, are detected along with fast neutrals, which are formed by charge-exchange between colder neutrals and energetic protons. The H_α emission recorded by the spectrometers along each line of sight is fitted by a sum of three Gaussians, as explained in [4]. We associate the narrowest Gaussian with the cold neutrals from the periphery and take the next broadest Gaussian to represent the thermal component because of its close relationship with the temperature measured by the NPA. In this work, we focus on the behaviour of the temperature and magnitude of the broadest Gaussian, which we take to come from the suprathermal proton population. For simplicity, we make the strong assumption of Boltzmann distribution for the suprathermal components of the impurities and protons. Although the species are not thermalized, this allows a one-parameter description of the distribution function, in terms of its effective temperature. Highly transient phases, i.e. at the initial stage of the NBI phase, have been excluded from the analysis.

When the spectral system is used for measuring He⁺ or C⁴⁺ line emissions at 4686 Å and 2271 Å, respectively, instead of H_α emission, only two Gaussians are used for the fit and the broadest one is again associated with the suprathermal component for these ions. This allows one to study suprathermal impurity ion dependence on charge and mass and might shed some light on suprathermal generation and confinement mechanisms. The lines used to study He⁺ (4686 Å) and C⁴⁺ (2271 Å in third diffraction order) fast populations are well isolated and prominent and if they have some low intensity lines that contaminate the line wing for some chords, the data analysis can account for them. The line integration smears out local information but cannot change orders of magnitude and main observational features. The light reflections are less important in the near UV where the C⁴⁺ emits at 2271 Å than where the He⁺ ion emits at 4686 Å. But the argument that rules out most of the possible instrumental effects that one can imagine is that the results obtained respond to the plasma conditions.

The spectral line shapes of bulk ions have been recorded in TJ-II plasmas using two high spectral resolution spectrometers that view the plasma at right angles perpendicular to the main magnetic field through fibre guides. One of the spectrometers achieves spatial resolution by simultaneously sampling nine equally spaced lines of sight. See figure 1(b) to see the present configuration. The channels are separated by 2.5 cm in the plasma and they are distributed so as to cover most of the plasma cross-section. The other spectrometer, which has a better time resolution, can only view one of the nine spatial channels at a time. For measuring the suprathermal components of the impurities, the integration times used in the ECRH phase have been from 40 to 300 ms. The experimental systems and data analysis methods are described in more detail in [10, 11]. The diameter of any of these light cones is not greater than 1 cm at the plasma centre.

An LP, figure 1(c), has already been developed for measuring the ion distribution function of ions escaping from TJ-II [7], whose energy spectrum in ECRH plasmas corresponds to a volume-averaged effective temperature similar to that observed by the spectroscopic method. In this work, we try to exploit the fact that our LP has a very high detection sensitivity compared with other LP designs, see [11] quoted in our [7]. In addition, it has been tuned to measure the energy distribution of escaping suprathermal ions either in ECRH or in NBI discharges. The tuning consists of finding an optimal location for the detector where the pulse pile-up effects are negligible and selecting the amplifier gain to avoid pulse saturation, within the analogue to digital converter range, during the NBI phase, but having sufficient pulse amplitude, well above noise, during the ECRH phase. For this purpose the LP is operated, for the first time in this range of energies, as a multichannel fast-ion energy spectrometer using the pulse height analysis [8].

A typical TJ-II discharge exhibits a range of densities and temperatures that goes from line-averaged densities from (0.3–1.6) × 10¹⁹ m⁻³ and T_e from 0.6 to 1.2 keV in the ECRH phase and similarly, (2–5) × 10¹⁹ m⁻³ and T_e from 0.3 to 0.6 keV in the NBI phase. The thermal ion temperature deduced from the central NPA system goes from about 70 to 120 eV when changing from the ECRH to the NBI heated phase.

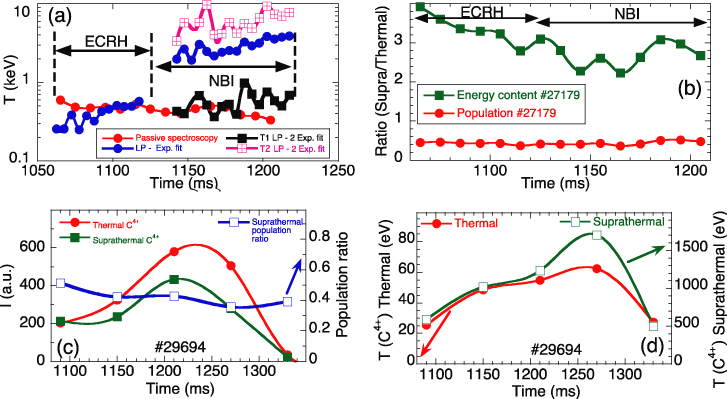
The pulse height analysis of the LP signal is carried out by software and permits one to obtain the suprathermal temperature–time evolution along a TJ-II discharge, as shown in the results depicted in figure 2(a), where the energy spectrum from the LP is fitted by one or two exponentials, each representative of a suprathermal distribution with effective temperature T. During the NBI phase the suprathermal energy distribution may be analysed by one or two components, whose results are given in the plot. The LP results in both ECRH and NBI phases are compared with time-resolved spectroscopic results, averaged along a central chord and looking at the perpendicular ion distribution. The LP probe in TJ-II is sensitive to ions with the pitch angle ranging from 10° to 40° sampled with particles detected by the probe over their orbits before loss (i.e. in the plasma). Since the LP probe measures energetic ions leaving the plasma, thus probably making it more sensible to trapped ions. The relevance of thermal and suprathermal components measured by spectroscopy, for a typical TJ-II discharge, is quantified for the case of protons in figure 2(b), where its relative population and relative energy content are depicted. Similar results regarding C⁴⁺ are depicted in figure 2(c), in both cases these data populations were obtained from spectroscopic data. We display in figure 2(d) the C⁴⁺ temperature–time evolution for both ion populations. Note that the suprathermal population exhibits a temperature that is a factor 20 higher than the thermal one. Below we will comment on the mass dependence of the suprathermal ion temperature once we present a broader range of data.

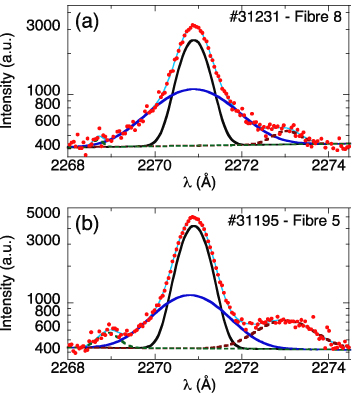
Zoom In Zoom Out Reset image size

The fittings of the 2271 Å line emission for two representatives chords in both ECRH and NBI discharges are shown in figures 3(a) and (b). These fittings have been performed with four Gaussians: for the thermal (black) and suprathermal (blue) components of C⁴⁺; and two for low intensity contaminating lines that we think the contaminating lines are the second order of two boron lines. In order to deduce the temperature of the main lines of interest, their line widths are corrected by the Gaussian instrumental function using the standard formula to deconvolve two Gaussians [10]. The instrumental function was measured using the 2536.5 Å line of an Hg lamp illuminating the system with a metallic diffuser producing a well uniform source. The temperatures obtained for the C⁴⁺ components in this analysis are 98 ± 8 eV and 1624 ± 181 eV (figure 3(a)) and 116 ± 6 eV and 1168 ± 101 eV (figure 3(b)). Note the scale of the vertical axis of both figures is logarithmic to enhance the smallest lines.

Zoom In Zoom Out Reset image size

Regarding the possibility of using other carbon lines, we must remark that in a device like TJ-II where very effective wall conditioning techniques are being used, prominent and well isolated lines of other carbon ions are not available for standard hot discharges. In addition, we have several procedures, apart from using long integration times, to perform these measurements. For example, measuring with He⁺ at the beginning of the day because we perform glow discharges in He every day, and therefore He⁺ emission is much higher. We cannot measure C⁴⁺ emission immediately after Li has been put on the wall, but we have to wait until the NBI beams have operated for a few days hitting the graphite tiles.

The confinement properties of suprathermal ions are important because it may be different than that of the thermal ones providing additional information on anomalous transport mechanisms. We have selected data obtained with the LP regarding three relevant ion confinement problems in TJ-II. First, we have studied how the ion particle confinement is a function of the energy, for that we have used a brief pulse of NBI in the middle of a long ECRH discharge. Second, we have studied the influence on the suprathermal ions of scanning the magnetic configuration in a single discharge using the C mode of TJ-II operation [13] on the suprathermal ions. Finally we have selected an isotopic exchange experiment in ECRH discharges of the TJ-II to assess the suprathermal behaviour.

3.1. Ion confinement energy dependence

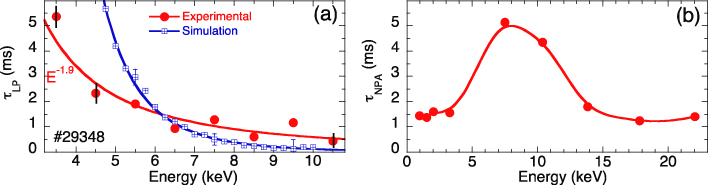
Short neutral-beam pulses (beam blips) are a convenient technique [14–16] for the study of the confinement of dilute populations of beam ions. However, usually those experiments could not discriminate the confinement behaviour as a function of ion energy. Although the neutron rate is a quantity integrated on the entire plasma volume, it retains some energy sensitivity, due to its cross-section which strongly weights the higher energies. A similar experiment has been performed in the TJ-II stellarator, by injecting a short NBI pulse (∼20 ms) in the middle of a constant density ECRH discharge. We have analysed an interesting aspect of the ion confinement, which highlights the capabilities of an LP when operating and handling the fast-ion response as a set of individual pulses. The ion pulse height (which is proportional to its energy) and the ion pulse number can be counted, using a windowed discrimination, as a function of time to investigate the time behaviour of the number of ion pulse counts per time interval under this well-controlled NBI pulsed experiment. In this experiment we have counted the number of ion pulses as a function of time, and the final decay after the NBI pulse is turned off is analysed by dN(E, t)/dE ∝ exp(−t/τ), where dN(E, t) represents the number of ions with energy E ± dE/2. The analysis has been performed for different values of the energy of ions escaping from the plasma and reaching the LP, showing a decreasing ion confinement time with ion energy (E^−1.9). This experimental result points in the same direction as the 1/ν regime in neoclassical theory [17] scaling with E^−7/2, which has been shown to be of relevance for TJ-II confinement [18]. To further clarify the importance of neoclassical transport in explaining the experimental results, the confinement of these energetic ion populations has been simulated numerically with a Monte Carlo code [19]. The procedure for estimating the ion confinement at a given energy consists in integrating the guiding centre trajectories of a group of ions at that energy and keeping track of the instant at which each ion leaves the last close flux surface. Note that this method does not attempt to simulate the NBI birth profile, which can be carried out with the FAFNER code [19], nor to self-consistently model the spatial and temporal ion slowing down distribution, but to study the residence time of ions at a given energy. Therefore, in the Monte Carlo simulation for a given energy all ions are started with the same initial energy and the initial position in magnetic surface, toroidal, poloidal and pitch angles is randomly chosen from a uniform distribution to guarantee the same weight of all regions in phase space. These simulation conditions try to reproduce the experimental conditions found by the ions moving radially out of the plasma. In integrating the ion trajectories the full complexity of TJ-II's magnetic field and the particle's Coulomb collisions with the experimental background electron and ion populations is taken into account. This last effect, along with the radial electric field is of minor importance for higher energies, but it is probably the cause of the higher confinement times at lower energies, since frequent pitch-angle scattering limits the time particles remain localized by collisionally removing them from the generous and abundant TJ-II ripples. Finally, the particle confinement time for each energy is obtained, as in the experimental analysis, by an exponential fit of the number of particles leaving the plasma as a function of time. The experimental as well as the simulated results appear in figure 4(a). The agreement between experimental data and simulation results is reasonably good for E > 5.5 keV but the theoretical points are much higher than the experimental ones for E < 5.5 keV.

Zoom In Zoom Out Reset image size

In addition, the TJ-II is equipped with a tangential compact NPA [20], which has also studied the time decay of the fast ions injected by the short NBI pulse [21]. A typical result obtained from the analysis of the tangential NPA is shown in figure 4(b), where we can see that the decaying behaviour of the confinement time with the ion energy is also observed for energies higher than 7 keV, although a decrease is observed in the low energy range which is not seen in the LP data. The confinement of a high energetic ion generated by the NBI heating system critically depends on its initial ionization position both in real as well as in velocity space. Ions born in the loss cone are quickly lost due to the lack of pitch-angle scattering. On the other hand, ions born in confined regions of phase space can survive longer and eventually will have time to explore other regions in phase space and reduce their energy via pitch-angle scattering. The fundamental difference between both experimental set-ups is that while the former views the plasma at right angles to the magnetic field, and therefore it is more sensitive to the average distribution of ions (including prompt losses), the second system views the plasma tangentially, sampling the passing ion region. The low confinement at low energy is an indication of the scattering pushing ions into the trapped region. The increase at higher energies is probably due to the heating from the 1/3 component of the NBI energy in the parallel direction. The final decrease at even higher energies simply reflects the gap between the 1/3 and 1/2 neutral-beam energies. Hence, figures 4(a) and (b) are not only not inconsistent but actually complementary. The ion confinement time depicted in figure 4(a), as we go towards the lowest energy range, tends to be comparable to the particle confinement time of thermal ions deduced from impurity injection experiments performed in the TJ-II stellarator [22].

It is well established that the transport of bulk (thermal) ions and electrons is due predominantly to turbulence [23], but ions of sufficiently high energy are commonly assumed to undergo little or no turbulent transport. The basis for this assumption is that the Larmor radii of such particles exceed the typical wavelengths of turbulent fields, which thus average to a value close to zero over a single gyration. Similar arguments have been advanced to suggest that energetic ions are unlikely to be significantly affected by the presence of short wavelength magnetohydrodynamic (MHD) modes. On the other hand, energetic ions are potentially susceptible to the neoclassical transport due to the magnetic field ripple of the device, which in the case of stellarators is an unavoidable consequence of its three-dimensional magnetic field. In general, it is found that ripple-induced transport is very sensitive to the amplitude of the different magnetic field components and their radial dependence, which in turn depends on the coil position and their distance from the plasma. This might be the most probable mechanism in TJ-II, since it is very high compared with other stellarators and also with tokamaks of similar dimensions.

3.2. Magnetic configuration effect on suprathermal ions

The influence of magnetic configuration on plasma confinement is a topic of great interest in TJ-II. A configuration scan between two selected values of ι (rotational transform) can be made in real time during a single discharge, using the so-called C mode, described in [13]. For stellarators it is more convenient to use $\iotabar ({\it iota\ bar}) =\iota /2\pi =1/q$, where q is the safety factor; $\iotabar_{0}$ corresponds to the value of rotation transform at the plasma centre, and $\iotabar_{\rm a}$ is the rotational transform at the plasma edge. We have used this TJ-II flexibility to explore suprathermal ion behaviour. The dynamic scan of configurations has a great advantage over discharges with static configurations, when one tries to explore whether the magnetic configuration plays a role in a physical phenomenon under observation, and also when one wants to sweep a particular magnetic island associated with a low order resonance and explore if it has any effect on some local diagnostic system tuned to some specific radius. One of the goals of these experiments has been to observe the movements of lower order resonances $\iotabar\,=\,3/2$, 5/3, 7/4, and their effect on plasma behaviour.

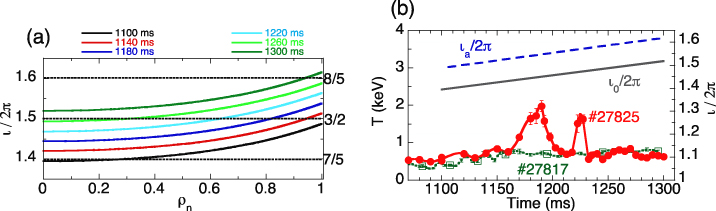
A magnetic scan was performed from the configuration 102_29_59 $(\iotabar_{0}\,=\,1.4)$ to configuration 90_41_59 $(\iotabar_{0}\,=\,1.57)$. These numbers are the currents in tenths of kiloamperes circulating for the three main coils of TJ-II. Time evolution of the theoretical vacuum rotational transform profile for this configuration scan (for discharge #27825) is presented in figure 5(a). The experiments performed in C mode show a clear effect of the rotational transform on suprathermal ion temperature measured with the LP; see figure 5(b). The temperature evolution in this configuration scan (discharge #27825) is very different compared with the one performed in a static magnetic configuration. As a reference, discharge (#27817) was performed in a static magnetic configuration 102_29_59. The electron densities for discharges presented on the graph are 0.67 × 10¹⁹ m⁻³ (#27825) and 0.51 × 10¹⁹ m⁻³ (#27817), respectively. The ECRH heating was deposed off-axis (at normalized radius ρ_n = 0.33). The total ECRH power was 400 kW. In this dynamic configuration scan we observe two clear temperature maxima. Probably they appear due to transition of the low order magnetic resonances by the edge (7/4) or by the centre (3/2). The LP measures suprathermal ions just outside the plasma edge, but this effect must be occurring inside the plasma. This effect has been reproducible and it is seen in a wide set of discharges and the discharge shown is representative of the entire set.

Zoom In Zoom Out Reset image size

A similar effect has been observed in other devices related to some MHD effect. A high-energy tail was observed in the ion distribution function following each internal reconnection event in the MAST spherical tokamak ohmic discharges. This phenomenon was explained in terms of runaway ion acceleration in the electric field induced by the reconnection [24]. Ion runaway in tokamaks was predicted theoretically by Furth and Rutherford three decades ago [25] and it has been suggested that it is present in solar flares [26] but to our knowledge spontaneous runaway of thermal ions has not been identified before in a modern tokamak. Magnetic reconnection effects on ions have also been reported in a RFP [27]. However, this type of effect seems to be implausible in TJ-II and one possible interpretation in our case is that vacuum fields are also changing as ι increases. It may be possible that fast-ion losses are localized in phase space and that, as ι varies, the overlap between these and the LP acceptance cone (in phase space) is modified, as to produce the results in figure 5(b). In other words, the physics of the losses would not change much but it becomes more or less detectable by the LP as the fields vary.

3.3. Isotopic effect in TJ-II suprathermal ions

The TJ-II stellarator was operated for several weeks with deuterium (D) in order to explore if the isotope effect, i.e. an improvement in confinement with ion mass $(\propto \sqrt {A_{{\rm i}}})$, can be observed in this device. Whilst this effect observed and studied for particle and energy confinement of bulk (thermal) plasma is quite robust in many tokamaks [28] and some linear machines [29], it has been observed only modestly and in the opposite direction in one stellarator [30]. Therefore, it is interesting to study whether any effect with ion mass can be seen in the suprathermal ion behaviour observed in pure ECRH TJ-II plasmas. The deuterium discharges have 25–30% of hydrogen (H) coming from the wall, as has been revealed by high-resolution spectroscopy [31].

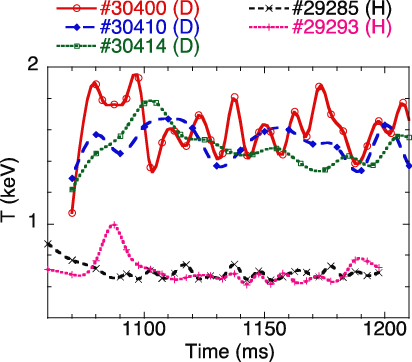
In addition, it is not possible to separate H⁺ and D⁺ signals in the LP data. However, the data obtained during several discharges with deuterium showed a significant difference compared with data for similar discharges performed with hydrogen, results are presented in figure 6. The magnetic configuration was 101_42_64 $(\iotabar_{0}\,=\,1.53)$. The power of both gyrotrons was 250 kW each. The observed effect on the temperature cannot be explained by the slight difference of the phosphor response to H⁺ or D⁺ and therefore an explanation based on basic mechanisms should be invoked.

Zoom In Zoom Out Reset image size

There has been a large amount of research regarding the non-Maxwellian electron energy distribution caused by ECRH [32, 33], and the non-Maxwellian ion energy distribution caused by ICRH [34]. However, little research has been carried out, theoretically or experimentally, into the ion energy distribution in plasmas heated by second harmonic electron cyclotron waves. In part, this is probably because well-refined diagnostics suitable for such a study are scarce. Consequently, we cannot compare our results with similar findings from other similar fusion machines, nor can we be guided by theoretical predictions. Therefore, due to the novelty of even empirical observations on this subject, we will present a set of results on the trend of the suprathermal behaviour for H⁺, He⁺ and C⁴⁺ in ECRH plasmas.

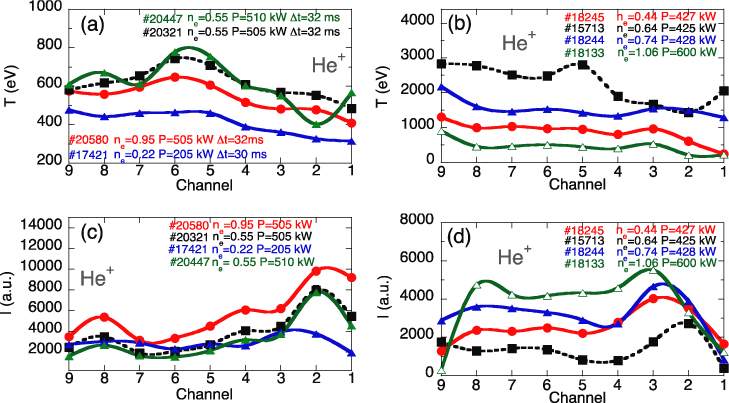
In figures 7(a) and (c) we present the temperature and the intensity of the proton suprathermal component along plasma chords numbered nine (top) to one (bottom), see figure 1(b), for a set of hydrogen discharges where the chord-averaged density was varied from 0.22 to 1.05 × 10¹⁹ m⁻³, and the injected ECRH power was varied from 200 to 510 kW. This set of data deserves a few comments: (a) the central chords (channels 5 and 6) show the largest change in suprathermal temperature (400 to 800 eV) in response to changing plasma operational parameters; (b) because of ∇B, the ions in TJ-II will drift towards the top of the machine at the measurement location, and the top channel measures a higher temperature than the bottom one; similar spatial variations in thermal ion temperatures have been measured using the NPA in TJ-II [35]; and (c) the temperature profile of the ion tail is not very peaked and exhibits a small variation across the plasma radius. We know for previous works that C⁴⁺ thermal emission typically peaks at effective radius (ρ_n = 0.5–0.6), in ECRH discharges, whereas it can peak closer to the centre during the NBI phase, where the central electron temperature is between 250–300 eV [36]. The case of He⁺ thermal emission has been considered also in a previous work [37].

Zoom In Zoom Out Reset image size

Figures 7(b) and (d) show data taken from helium discharges where the He⁺ (4686 Å) emission line was fitted with two Gaussians. The temperatures of the broadest Gaussians are plotted in figure 5(b) as a function of the spatial channel number for a range of densities ((0.44–1.06) × 10¹⁹ m⁻³) and injected powers (400 to 600 kW). All discharges correspond to on-axis heating, except #20321, which was heated off-axis and with non-zero n_|| (parallel wave vector) and has the highest value of temperature (square black points). The chord-integrated emission intensity of the He⁺ emission is depicted in figure 7(d) for the same set of discharges. Note the rather flat temperature profile for most cases and that the temperature of the top channels is higher than the bottom ones, as was seen in hydrogen discharges.

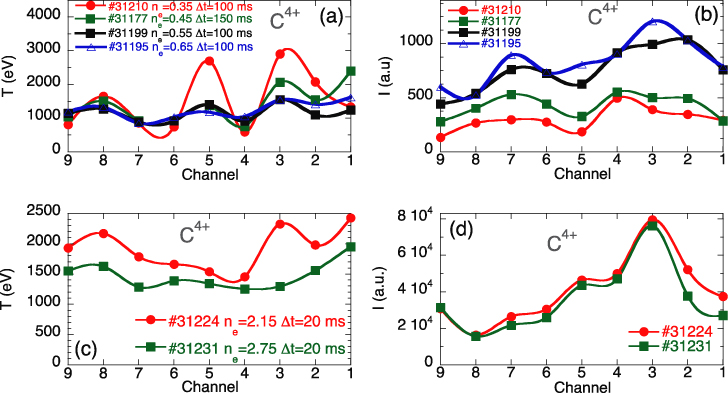
The suprathermal ion observation made on protons and He⁺ are more peripheral than using for instance the emission of C⁴⁺. The interest of attacking this problem with inner ions and with different charge and charge to mass ratio is to explore a possible dependence of the heating on any of those parameters, and also try to reach the plasma centre. However, it is more difficult to detect the suprathermal component in C⁴⁺ because longer integration times are needed and the spectral zone must be free of contaminant lines when observing the 2271 Å line in third diffraction order, which is not always possible. However, a few selected observations have been possible with this ion either in ECRH plasma or in NBI plasmas. In figure 8(a) we display the suprathermal temperatures for a set of ECRH discharges, with different electron densities, along with their chord-integrated emission (reflecting ion population) in figure 8(b); similarly for NBI discharges in figures 8(c) and (d). It is worthy to remark the spatially modulated structure observed in the suprathermal temperature displayed in figure 8(a), which is more pronounced at the lowest density; whilst the integrated intensities are somewhat hollowed and with some asymmetry for upper and lower chords which could be explained for the different lengths of the chord inside the plasma and possibly some impurity concentration asymmetry.

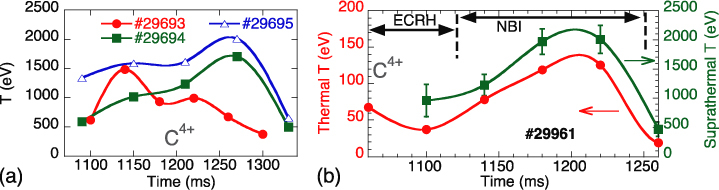
Zoom In Zoom Out Reset image size

The time behaviour of C⁴⁺ suprathermals in typical ECRH discharges is shown in figure 9(a) for a set of discharges with insignificant operational changes, which highlights the sensitivity of this population to non-trivial nuances of the TJ-II plasma. The temperature of C⁴⁺ suprathermals, along with that of the thermal one, is depicted in figure 9(b) for an NBI discharge. The effect of the fast neutrals is clearly noted on both thermal and suprathermal components. During the NBI phase both thermal and suprathermal temperatures increase.

Zoom In Zoom Out Reset image size

We have attained several conclusions: (a) the typical temperature of the suprathermal ions is a factor 4 higher than the thermal one in the case of protons and much higher for He⁺ and C⁴⁺, suggesting an almost linear dependence with the particle mass; (b) in many cases the ion energy content of this suprathermal component is comparable to the energy content of the thermal one with relevant implications for the TJ-II energy balance; (c) an isotope effect on suprathermal hydrogen isotopes is clearly seen; (d) the dependence of suprathermal confinement time with the energy is clearly observed; and (e) the influence of the TJ-II magnetic configuration scan is echoed in the suprathermal temperature measured by the LP.

All these results represent a true challenge for theories capable of explaining its generation: suprathermal particles constitute an excellent probe of physical mechanisms inside a high-temperature plasma, complementary of the thermal ones. Its time behaviour during the analysis of pulsed experiments has allowed the determination of the confinement time of fast ions as a function of energy and detection system, LP or NPA. The confinement time deduced from the LP system, which is more sensitive to the trapped ion dynamics, is found to decrease as the energy increases, a trend that has been predicted by the results of a simulation with the physical features of TJ-II plasmas (collisions, magnetic configuration, etc), except fluctuations. The quantitative agreement between experimental and theoretical fast-ion confinement time is reasonably good at the highest energies, but is worse for the low energy range, where the importance of fluctuations increases as the Larmor radius decreases. On the other hand, no attempt was made to simulate the characteristics of the confinement time deduced from the NPA system, which is more sensitive to the parallel ion dynamics, since they are strongly correlated with the NBI beam energy components.

This work was partially funded by the Spanish Ministry of Science and Education under Projects Nos ENE2010-19109, ENE2010-19676 and ENE2012-33219. D.J.R. thanks the Juan de la Cierva programme of the MICINN, JCI-2009–05681, for financial support. The authors are grateful to Dr E. Hollmann for a critical review of the manuscript.