ABSTRACT
Most galaxies possibly contain some binaries, and more than half of Galactic hot subdwarf stars, which are thought to be a possible origin of the UV-upturn of old stellar populations, are found in binaries. However, the effect of binary evolution has not been taken into account in most works on the spectral fitting of galaxies. This paper studies the role of binary evolution in the spectral fitting of early-type galaxies, via a stellar population synthesis model including both single and binary star populations. Spectra from ultraviolet to optical bands are fitted to determine a few galaxy parameters. The results show that the inclusion of binaries in stellar population models may lead to obvious change in the determination of some parameters of early-type galaxies and therefore it is potentially important for spectral studies. In particular, the ages of young components of composite stellar populations become much older when using binary star population models instead of single star population models. This implies that binary star population models will measure significantly different star formation histories for early-type galaxies compared to single star population models. In addition, stellar population models with binary interactions on average measure larger dust extinctions than single star population models. This suggests that when binary star population models are used, negative extinctions are possibly no longer necessary in the spectral fitting of galaxies (see previous works, e.g., Cid Fernandes et al. for comparison). Furthermore, it is shown that optical spectra have strong constraints on stellar age while UV spectra have strong constraints on binary fraction. Finally, our results suggest that binary star population models can provide new insight into the stellar properties of globular clusters.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Binaries are possibly common in most galaxies, and their evolution is often different from single stars if binary components are not too far away (Eggleton 2006). In our Galaxy, the fraction of binaries has been shown to be as large as about 50%. Binaries are found in different parts of the Galaxy, e.g., Galactic field, halo, and thick and thin disks (Duquennoy & Mayor 1991; Fischer & Marcy 1992; Mayor et al. 1992; Raghavan et al. 2010; Carney et al. 2005). In addition, most stars that are more massive than the Sun are born in binaries (Brinchmann 2010), and the more massive the stars, the larger the fraction of binaries (Lada & Lada 2003). Therefore, binaries are absolutely important for understanding the stellar populations of galaxies, and it is necessary to study the role of binary evolution in stellar population studies. The importance of binaries has been recently listed as one of six important challenges in stellar population studies in the next decades by Brinchmann (2010). However, most previous works used single stars for modeling stellar populations because of the complexity of binary evolution and more input parameters in binary star stellar population synthesis (bsSPS). In addition, astronomers hope that binary evolution does not change the results of single star stellar population (ssSP) studies too much. If this is true, selecting single star stellar population synthesis (ssSPS) will be a good choice for stellar population studies.
Meanwhile, a few works (e.g., Li et al. 2006, 2012a; Han et al. 2007; Li & Han 2008a, 2008c, 2008b; Hernández & Bruzual 2011) have tried to investigate the effects of binary evolution on stellar population studies and have used the binary star stellar population (bsSP) model in a few works (e.g., Li et al. 2006, 2010, 2012b; Marks & Kroupa 2011, 2012). These show that binary evolution is able to reproduce many interesting results such as blue stragglers, red stragglers, extended main sequence (Li & Han 2008a; Li et al. 2012b), and UV flux excess (hereafter UV-upturn) in elliptical galaxies (e.g., Han et al. 2007; Li & Han 2008a; Li et al. 2012a), without any special assumptions such as very old age or high mass-loss (see Lee 1994; Park & Lee 1997; Bressan et al. 1994; Yi et al. 1997 for comparison). Binary evolution has been shown to be a natural explanation for the UV-upturn of elliptical galaxies, because more than half of Galactic hot subdwarf stars are found in binaries (Ferguson et al. 1984; Allard et al. 1994; Thejll et al. 1995; Ulla & Thejll 1998; Aznar Cuadrado & Jeffery 2001; Maxted et al. 2001; Williams et al. 2001; Reed & Stiening 2004), and it is well established that the vast majority of (and quite possibly all) hot subdwarfs are the results of binary interactions (Han et al. 2007). On the other side, the widely used ssSP models fail to reproduce UV-upturn for old stellar populations under normal assumptions. Thus it suggests that binaries are important and possibly the main contributors to the UV-upturn spectra of old populations. In addition, this shows that binaries can obviously change the results of simple stellar population (SSP) studies (Li & Han 2008b), when spectral line indices or colors are used to determine stellar population parameters (age and metallicity) of galaxies. Although the importance of binaries has been shown, we are far from understanding the role of binaries well. Deeper and more detailed studies are therefore needed. Because it has been shown that binary evolution leads to significant change in the UV and optical spectra of populations (Li & Han 2008b; Li et al. 2012a), and fitting such spectra are the basis of most stellar population studies (see the review of Walcher et al. 2011 or papers such as Cid Fernandes et al. 2004, 2005; Lu et al. 2006; Tojeiro et al. 2007, 2009; Koleva et al. 2008, 2009), it is important to study the effect of binaries on full spectrum fitting.
This work aims to investigate the potential importance of binary evolution in spectral studies of early-type galaxies. The reason for studying early-type galaxies is that their stellar populations are relatively simple, which can possibly be modeled by two population components (Li et al. 2012a). Our main purpose is to study how the results of spectral fitting can be changed by using bsSP models instead of ssSP models. UV–optical spectra will be fitted by homogeneous ssSP and bsSP models that vary from including binary interactions to not including binaries.
The structure of this paper is as follows. Section 2 introduces stellar population models, and Section 3 describes spectral synthesis. Section 4 then presents the spectral fitting code (BS2fit) used in this work. In Section 5, for some mock galaxies, the galaxy parameters determined by ssSP and bsSP models are compared. Then, in Sections 6 and 7, the spectra of a few galaxies and star cluster groups are used to perform some similar tests. Next, Section 8 shows the degenerate effects of binary fraction and stellar population age on spectra of populations. Finally, Section 9 summarizes and discusses the results.
2. STELLAR POPULATION MODEL
An advanced stellar population synthesis model including both ssSPs and bsSPs (Li & Han 2008a; Li et al. 2012a) is used for this work. This model supplies homogeneous spectra for both simple and composite stellar populations (SSPs and CSPs) with or without binary interactions. This makes it possible to study the resulting changes caused only by binary evolution. In the following two subsections, we introduce the stellar population synthesis model for SSPs and CSPs, respectively.
2.1. Simple Stellar Populations
Simple stellar populations (SSPs) are built as follows. First, some stars (primary components of binaries) are generated following an initial mass function (IMF) of Chabrier (2003) with lower and upper mass limits of 0.1 and 100 M☉, respectively. Then for each binary, the mass of its secondary component is generated by taking a uniform distribution for the mass ratio (q, 0–1) of the secondary to the primary component (Mazeh et al. 1992; Goldberg & Mazeh 1994). The separation (a) between two binary components is given following an assumption that the fraction of binaries in an interval of log(a) is constant when a is large (10 R☉ < a < 5.75 × 106 R☉) and it falls off smoothly when a is small (⩽10 R☉) (Han et al. 1995), which can be written as
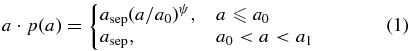
where asep ≈ 0.070, a0 = 10 R☉, a1 = 5.75 × 106 R☉, and ψ ≈ 1.2. The eccentricity (e) of each binary system is generated according to a uniform distribution. In this method, each population contains about 50% binaries with orbital period less than 100 yr, which is similar to the typical binary fraction of the Galaxy. When building binary star simple stellar populations (bsSSPs), the interactions between two binary components are taken into account when evolving stars, but all stars are evolved separately when building single star simple stellar populations (ssSSPs). All stars of an SSP are assumed to form in a star burst and have the same metallicity. In order to reproduce the IMF with enough accuracy via a Monte Carlo process, 4,000,000 binaries are obtained for a population according to the result of our tests.
After the generation of population stars, all stars are evolved using the rapid stellar evolution code of Hurley et al. (2000, 2002; Hurley code), which uses some fitting formulae to calculate the evolution of both binary and single stars. The formulae used for rapid single-star evolution (SSE) is based on the stellar evolution tracks computed by Pols et al. (1998; OVS tracks). Thus the tracks of Pols et al. (1998) are actually used for evolving single stars. The rapid binary-star evolution (BSE) code is a natural extension of the SSE algorithm. It includes eccentric orbits and stellar spins, which are subject to tidal circularization and synchronization. In addition, BSE updated the treatment of processes such as Roche lobe overflow, CE evolution, and coalescence by collision compared to previous works, e.g., Tout et al. (1997). Therefore, BSE is also mainly based on the stellar evolution tracks of Pols et al. (1998). We use the Hurley code because there are no complete tracks for the evolution of binaries. Most binary evolution processes such as mass transfer, mass accretion, common-envelope evolution, collisions, supernova kicks, and angular momentum loss are included for bsSPs. Different mass transfer mechanisms, i.e., dynamical mass transfer, nuclear mass transfer, and thermal mass transfer, are taken into account using the results of many works (e.g., Tout et al. 1997; Hjellming & Webbink 1987). One can see Hurley et al. (2002) for more details. Some default values for the Hurley code, i.e., 0.5, 1.5, 1.0, 0.0, 0.001, 3.0, 190.0, 0.5, and 0.5, are used for wind velocity factor (βw), Bondi–Hoyle wind accretion faction (αw), wind accretion efficiency factor (μw), binary enhanced mass loss parameter (Bw), fraction of accreted material retained in supernova eruption ( ), common-envelope efficiency (αCE), dispersion in the Maxwellian distribution for the supernovae kick speed (σk), Reimers coefficient for mass loss (η), and binding energy factor (λ), respectively. We use these default values because they have been checked in the work of Hurley et al. (2002). Although these default values remain somewhat large uncertainties, the results for spectral stellar population synthesis will be not affected too much by the uncertainties in these parameters, according to a test in our previous work (Li et al. 2012a). In addition, because the Hurley code uses some fitting formulae to calculate the evolution of stars, it causes about 5% uncertainty in the evolutionary parameters of stars.
), common-envelope efficiency (αCE), dispersion in the Maxwellian distribution for the supernovae kick speed (σk), Reimers coefficient for mass loss (η), and binding energy factor (λ), respectively. We use these default values because they have been checked in the work of Hurley et al. (2002). Although these default values remain somewhat large uncertainties, the results for spectral stellar population synthesis will be not affected too much by the uncertainties in these parameters, according to a test in our previous work (Li et al. 2012a). In addition, because the Hurley code uses some fitting formulae to calculate the evolution of stars, it causes about 5% uncertainty in the evolutionary parameters of stars.
The evolutionary parameters of stars are finally transformed to the spectral energy distributions (SEDs; or spectra) of stellar populations by the BaSeL 3.1 spectral library (Lejeune et al. 1997, 1998). The library is chosen here because of its wide wavelength coverage and reliability. The uncertainties in the spectra of populations caused by the spectral library is small (about 3% on average). In the same way, the homogenous spectra of both ssSSPs and bsSSPs are computed. Note that the only difference between these two kinds of models is that bsSSPs take binary interactions into account but ssSSPs do not.
When comparing the bsSSP spectra to ssSSP spectra, we find obvious differences. The left panels of Figure 1 show the comparison of the spectra of two kinds of populations. It is clear that the spectra of bsSSPs and ssSSPs are different, especially in the UV band. Many old (>3 Gyr, bottom lines) bsSSPs show UV-upturn spectra, which is mainly caused by hot subdwarf and blue straggler stars (e.g., Han et al. 2007), but all old ssSSPs do not have similar spectra. Because the UV-upturn phenomenon has been observed in many elliptical galaxies (Burstein et al. 1988; O'Connell 1999), which are usually thought to be SSPs, our result suggests that bsSSPs can be better fitted to early-type galaxies than ssSSPs. In binary evolution, the formation channels for hot subdwarfs are common-envelope ejection, stable Roche lobe overflow, and merger of helium white dwarfs (see also Han et al. 2007).
Figure 1. Comparison of SEDs of single and binary star populations. Gray lines are single star populations, while red lines are binary star populations. The left and right columns show the results of simple and composite stellar populations (SSPs and CSPs), respectively. Note that stellar age increases from top to bottom in each panel.
Download figure:
Standard image High-resolution image2.2. Composite Stellar Populations
The SEDs of CSPs are built on the basis of SEDs of SSPs. Because there is no common result for the star formation histories (SFHs) of early-type galaxies, a simple method is used to model CSPs. In detail, each CSP is assumed to contain a pair of old and young components with the same metallicity. This assumption is in agreement with previous studies' findings that early-type galaxies are dominated by old populations and there is only a little fraction of young populations in such galaxies. The mass fraction of the young component is assumed to be dependent on the ages of two components of CSPs, which is calculated by formula (2). This means that the mass fraction of the young component declines exponentially with increasing difference between the ages of old and young components. This agrees with previous studies on the SFHs of early-type galaxies (e.g., Thomas et al. 2005):

where F2 is the mass fraction of young component; t1 and t2 are the ages of old and young components of a CSP, respectively. τ is a free parameter, which denotes the speed of the declination of star formation. It is related to the SFHs of galaxies, and there is no fixed value. As a standard model, τ is taken to be 3.02 Gyr, which is estimated by Li & Han (2007). This value can reproduce the observational fraction of bright early-type galaxies with recent (⩽1 Gyr) star formation at a level more than 1%–2% (Yi et al. 2005).
By the above method, the SEDs of single and binary star composite stellar populations (ssCSPs and bsCSPs) are calculated. In the right panels of Figure 1, the SEDs of two kinds of CSPs are compared. For some pairs of ssCSPs and bsCSPs with the same parameters, we see clear differences between the SEDs of two kinds of populations. Similar to the case of SSPs, the UV spectra of two kinds of populations are obviously different. In addition, we find that both ssCSPs and bsCSPs can show UV-upturn spectra, but UV-upturn comes from different origins. The UV-upturn of bsCSPs is mainly caused by binary evolution, but that of ssCSPs is caused by young stars. This suggests that bsCSP and ssCSP models possibly give different estimates for the SFHs of early-type galaxies. When we compare our findings with a previous result (Maraston & Thomas 2000), which concludes that UV-upturn is most likely due to late evolutionary phases of metal-rich stars, it is shown that bsCSP models have obvious advantage for reproducing UV-upturn. In detail, when ssCSP models are used, a metal-poor subcomponent is needed (Maraston & Thomas 2000), but it causes another question, i.e., how the metallicities of two population components are related. If bsCSP models are used instead of ssCSP models, this problem will no longer exist. Therefore, even though CSPs are really needed for interpreting the UV-upturn spectra of old populations, bsCSPs are a good choice.
3. SPECTRAL SYNTHESIS
The observed spectra of stellar populations are built based on the SEDs of CSPs. According to our model, each CSP is described by three parameters: metallicity Z, old-component age t1, and young-component age t2. The effects of stellar velocity dispersion σ*, extinction from dust around stellar population, redshift, and the extinction caused by the Milky Way are added to the SEDs of CSPs to form the observed spectra. Similar to the works of Cid Fernandes et al. (2005), the line-of-sight stellar motions are modeled by a Gaussian distribution G centered at velocity v* and with dispersion σ*. The effect of dust around the population, which is parameterized by V-band optical depth τV, is modeled following the work of Charlot & Fall (2000). When modeling the Galactic extinction, which can be parameterized by V-band extinction AV, the extinction law of Cardelli et al. (1989) with RV = 3.1 is adopted. The observed flux (fλ) at wavelength λ can be expressed by
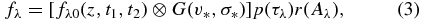
where fλ0 is the flux of a CSP with three parameters (Z, t1, t2), G(v*, σ*) is a Gaussian distribution with mean and standard deviation of v* and σ* respectively, p(τλ) is the percentage of energy that passes through the dust with optical depth of τλ, r(Aλ) is the fraction of energy after the extinction (Aλ) of the Milky Way. ⊗ denotes the convolution operator.
Figure 2 gives two examples for the synthesis of the spectra of an ssCSP and bsCSP pair with the same model inputs. We see that line-of-sight stellar motions (redshift and stellar velocity dispersion) obviously affect the wavelength range and strength of absorption lines, but stellar velocity dispersion does not affect continuum spectra too much. Meanwhile, the dust around stellar population and the Milky Way affects the whole spectra. We can also see significant differences between the spectra of ssCSPs and bsCSPs from this figure.
Figure 2. Formation of synthetic SEDs of single (left) and binary (right) star composite stellar populations (ssCSP and bsCSP). Green lines show SEDs of two simple stellar populations (SSPs) with age = 10 Gyr and solar metallicity (Z = 0.02), while black, red, blue, cyan, and purple lines are SEDs after gradually adding the effects of second star formation, stellar velocity dispersion, dust in the galaxy, redshift, and Galactic extinction into the original SEDs of two SSPs.
Download figure:
Standard image High-resolution image4. SPECTRAL FITTING: BS2fit CODE
Spectral fitting is an important technique to determine many properties of galaxies, e.g., redshift, stellar metallicity, age, velocity dispersion, mass, and dust extinction, because different wavelengths are usually dominated by various physical processes. Thus it is a good choice to study the role of binary evolution in stellar population studies via spectral fitting. Although there are some available spectral fitting codes, e.g., MOPED (Heavens et al. 2000), PLATEFIT (Tremonti et al. 2004), STARLIGHT (Cid Fernandes et al. 2004, 2005), VESPA (Tojeiro et al. 2007, 2009), STECKMAP (Ocvirk et al. 2006), sedfit (Walcher et al. 2006), NBURSTS (Chilingarian et al. 2007), and ULYSS (Koleva et al. 2009), they are not very suitable for this work. First, all of them are developed for some special purposes so that their fitting methods and wavelength coverages are not suitable for this work. For example, STARLIGHT aims to fit the optical spectra of Sloan Digital Sky Survey galaxies, but our work needs a wider wavelength coverage. VESPA studies the SFHs of galaxies via some binned parameters, but we want to perform more accurate studies. Furthermore, there are some other limitations to using these codes, e.g., the dependence on an internet connection or unaltered procedures. Therefore, we decide to create a new code. We call our new code binary star to fit (hereafter BS2fit), which can be used for spectral fitting via both bsSPs and ssSPs, within a wide wavelength range from the UV to the optical band. The new code can be briefly introduced as follows.
BS2fit code will be revised and updated.4 At this stage, BS2fit aims to determine a few parameters of early-type galaxies or globular clusters (GCs) from observed spectra using bsSP or ssSP models. An observed spectrum is assumed to be determined by eight input parameters, i.e., Z, t1, t2, v*, σ*, τV, AV, and total stellar mass M*. Because there are so many input parameters, it is not easy to get a best-fit result by directly searching for the combination of parameters with minimum χ2 in a high-resolution parameter grid. Therefore, we divide the fitting task into three parts. First, line-of-sight velocity (or redshift) is determined by a few methods that are widely used (e.g., absorption or emission line fitting and cross-correlation analysis; see, e.g., Colless et al. 2001). Then the Galactic extinction parameter AV is determined from the direction of the galaxy and the dust map of the Milky Way (e.g., Burstein & Heiles 1982; Schlegel et al. 1998). Finally, the other parameters are determined based on fixed redshift and Galactic extinction.
Although determining v* and AV separately has made the fitting process much faster, it is still difficult to obtain the result through a direct search on a personal computer. Two new techniques are therefore used to make the fitting significantly quicker. One is to estimate the possible ranges of parameters using SSP models before comparing the observed spectrum to those of CSPs. We call this procedure SSP-fitting. This is very effective, because it guides the code to search in only limited ranges of parameters. This method is also reliable for most populations, because SSPs usually estimate lower metallicities, smaller stellar velocity dispersions, and younger ages for populations compared to CSPs. Figure 3 shows how the ranges of parameters of 74 test stellar populations are related to SSP-fitted parameters. On average, the parameter ranges of about 95% of CSPs can be well estimated from SSP-fitting. The other technique for speeding up the fitting is to compare continuum spectra before comparing whole spectra. This skips many populations according to their continuum difference from the observed spectra. This can be done because there is a maximum change in continuum spectra corresponding to the effects of dust extinction and stellar velocity dispersion when their ranges are given.
Figure 3. Comparison of SSP-fitted and real parameters of 37 ssCSPs and 37 bsCSPs. Open and filled squares are for ssCSPs and bsCSPs, respectively. Solid lines show the ranges for searching the final parameters in CSP-fitting, while dashed lines are unity lines. t1 is in Gyr and σ* is in km s−1.
Download figure:
Standard image High-resolution imageBesides the determination of v* and AV, the main procedures of spectral fitting include two steps. The first is to estimate the ranges of Z, t1, σ*, and τV via SSP-fitting (Figure 3). This also provides the best SSP-fit results for galaxies. The other is to determine the stellar population parameters (Z, t1, and t2, M*), extinction parameter (τV), and kinematics parameter (σ*) by comparing the observed spectra with those of CSPs with parameters in the ranges that are determined by SSP-fitting. We call this procedure CSP-fitting. It is actually a procedure to take the effects of minor and young populations into account. Because stars are possibly not formed simultaneously in most galaxies, CSP-fitting usually reports different results compared to SSP-fitting (see Figure 3).
In the spectral fittings, BS2fit determines stellar population parameters by comparing the observed spectra to various model spectra and minimizing the difference between model and data. In detail, the goodness of a fit is judged by
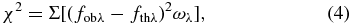
where fobλ and fthλ are the observed and theoretical spectra, while ωλ is the weight for the wavelength λ. The best-fit result corresponds to a minimum χ2. In most cases, ωλ can be expressed using observational error:

However, ωλ can also be assigned to fixed values according to special requests.
We mask out some emission line regions as they can affect the final results obviously. According to some previous works (McQuade et al. 1995; Panter et al. 2007; Tojeiro et al. 2007, 2009), the following emission-line regions in every spectrum's rest frame wavelength range are masked out by setting ωλ to zero: 1213–1219, 1548–1550, 1637–1643, 1905–1911, 2323–2329, 2421–2427, 2796–2803, 3423–3429, 3711–3741, 4087–4117, 4325–4355, 4846–4876, 4944–4974, 4992–5022, 5885–5900, 6535–6565, 6548–6578, 6569–6599, 6702–6732, 6716–6746, 6728–6734, 7132–7138, and 7319–7330 Å.
Because we want to make the results accurate enough, a high-resolution grid of parameters is taken. In detail, stellar metallicity (Z) is from 0.0003 to 0.03, with an interval of 0.0001 when Z is less than 0.001, and an interval of 0.001 for higher metallicity. The old-component age (t1) of populations is in the range of zero to 15 Gyr, with an interval of 0.1 Gyr, and the young-component age (t2) decreases from t1 to zero. Stellar velocity dispersion, σ*, changes from 0 to 350 km s−1 by a step of 10 km s−1, and the optical depth (τv) is between 0 and 1.5, with an interval of 0.01. Note that the ranges of σ* and τv are chosen according to some previous works, e.g., Cid Fernandes et al. (2005) and Tojeiro et al. (2007).
In order to check the accuracy of the BS2fit code, Figures 4 and 5 show the input versus recovered values of mass-weighted age 〈t*〉M, luminosity-weighted age 〈t*〉L, Z, t1, t2, v*, σ*, τV, and M* of 37 ssCSPs (open squares) and 37 bsCSPs (filled squares). In the test relating to Figure 4 all wavelengths are assumed to be the same weight because there is no error in the spectra, while in the study corresponding to Figure 5 the weight of each wavelength is set to be 1/ , where Eoλ is the observational error. The stellar mass of each population is calculated from the input flux at 5500 Å and mass-to-light ratio of the best-fit population. We see that when there is no error in input spectra, the BS2fit code can well recover most parameters (Figure 4), although the t2 values of some populations with large (>3.5 Gyr) input t2 are not recovered accurately because of the degeneracy effects of various parameters on the same spectra. Note that the input spectra of an ssCSP and bsCSP pair with the same set of input parameters are usually different.
, where Eoλ is the observational error. The stellar mass of each population is calculated from the input flux at 5500 Å and mass-to-light ratio of the best-fit population. We see that when there is no error in input spectra, the BS2fit code can well recover most parameters (Figure 4), although the t2 values of some populations with large (>3.5 Gyr) input t2 are not recovered accurately because of the degeneracy effects of various parameters on the same spectra. Note that the input spectra of an ssCSP and bsCSP pair with the same set of input parameters are usually different.
Figure 4. Comparison of input and recovered parameters of ssCSPs and bsCSPs. The input spectra have no error. Squares have the same meanings as in Figure 3. The solid line is a unity line. 〈t*〉M and 〈t*〉L denote mass and luminosity-weighted age, respectively. Z, log(M*), t1, t2, σ*, and τv represent metallicity, logarithmic stellar mass, old-component age, young-component age, stellar velocity dispersion, and optical depth. 〈t*〉M and 〈t*〉L are in Gyr, and M* is in solar mass.
Download figure:
Standard image High-resolution imageFigure 5. Similar to Figure 4, but for some input spectra with S/N = 10. Gray error bars show the σ uncertainties of galaxy parameters.
Download figure:
Standard image High-resolution imageIf there are uncertainties (signal-to-noise ratio (S/N) = 10) in input spectra (Figure 5), BS2fit code reports obviously larger ages (especially t1) for most populations. This because the change of spectra is less sensitive to the age change of old populations. Moreover, the uncertainties in input spectra result in lower estimates for stellar metallicities of some populations, because the change of spectra has different sensitivities to the metallicity changes of metal-poor and -rich populations. The deviations in stellar age and metallicity are also related to the well-known age–metallicity degeneracy. Therefore, the S/N of observed spectra is crucial for constraining the stellar metallicities and ages of galaxies. In addition, we see that bsCSP and ssCSP models usually lead to similar differences between the input and recovered parameters. This means that the BS2fit code can be used to study the difference between galaxy parameters, which are caused by using various (bsCSP and ssCSP) models, although the values of the parameters may be not so accurate. Note that the fitted parameters and uncertainties are given statistically by taking the average and 1 σ deviation of the results of fitting some perturbed spectra that are generated randomly according to the observational uncertainty (see also Cid Fernandes et al. 2005; Tojeiro et al. 2007).
5. RESULTS FROM MOCK GALAXIES
This section studies the difference between bsSP- and ssSP-fitted results, via a sample of 37 mock galaxies, which covers wide parameter ranges. We assume that all mock galaxies are bsCSPs, as almost all galaxies may contain some binaries. The mock populations are generated following the generation of bsCSPs in Section 2.2, in which each bsCSP contains two components with the same metallicity but different ages. The SFH is therefore expressed by formula (2). In addition, because any observed spectrum possibly contains some uncertainties, the effect of observational uncertainties is taken into account. Similar to the previous section, the S/N of spectra is set to 10, and ωλ is given as 1/ .
.
Figure 6 shows the comparison of bsSP- and ssSP-fitted parameters of 37 bsCSPs (mock galaxies). We see that ssSP- and bsSP-fitted results for mass and luminosity-weighted ages, metallicity, stellar mass, old-component age, stellar velocity dispersion, and galactic dust extinction are roughly consistent when uncertainties are taken into account. In particular, ssSP and bsSP-fitted stellar masses are almost the same. However, for mock galaxies with ssSP-fitted t2 younger than 3.5 Gyr, bsSP models measure much older young population components for most mock galaxies. This suggests that ssSP models usually measure more recent star formations for early-type galaxies, compared to bsSP models. In this case, many early-type galaxies may not contain as many recent star formations as the results of (Chen et al. 2012; 10 times more galaxies formed 5% more of their stars over the last Gyr), which was obtained using some ssSP models.
Figure 6. Comparison of ssSP and bsSP-fitted parameters of 37 bsCSPs. Points and error bars show mean parameters and σ uncertainties, respectively. "ss-fitted" and "'bs-fitted" denote ssSP-fitted and bsSP-fitted results, respectively.
Download figure:
Standard image High-resolution imageMock galaxies are actually a very useful tool in the spectral studies of stellar populations. For example, Pforr et al. (2012), for extensive experiments of fitting mock galaxies, studied both passive and star-forming galaxies, and concluded that SSPs give lower ages and wavelength coverage is important for SED fitting.
6. RESULTS FROM REAL GALAXIES
In this section, we try to compare the galaxy parameters that are determined via ssSP and bsSP models, for a small sample of 10 galaxies, in which a spiral galaxy is included. The data are selected from a catalog of UV–optical spectra of 99 local galaxies, which is available on the Internet.5 The advantage of using these data is the wide wavelength coverage from the UV to the optical band. Because binaries obviously affect UV spectra (Han et al. 2007; Li & Han 2008a; Li et al. 2012a), such data seems ideal for exploring the effect of binary evolution on spectral fitting. In addition to some emission lines, we also mask out the spectra around two conjunction wavelengths (2000 and 3000 Å) as the two parts contain obviously larger uncertainties. In addition, because the quality of optical spectra is better than UV spectra, optical spectra are given higher weights by using S/N = 8, while the S/N of UV spectra is taken to be 7. The S/N values are given according to a description of the data (Kinney et al. 1996), but the data quality seems to be not good as S/N = 8, because the minimum χ2 values of fittings are obviously larger than 1.
Using the BS2fit code, six parameters of 10 galaxies are determined, and the ssSP- and bsSP-fitted results are then compared. For convenience, we take the redshifts of 10 galaxies from NASA/IPAC Extragalactic Database (NED). The original results were obtained by Wegner et al. (2003), da Costa et al. (1991), Tully et al. (2008), Koribalski et al. (2004), Huchra et al. (1999), and Denicoló et al. (2005). The Galactic extinctions are calculated using the extinction calculator of NED, which uses the data and technique of Schlegel et al. (1998). Tables 1 and 2 list the ssSP- and bsSP-fitted parameters of 10 galaxies. Because the quality of observed spectra is not very good, the result for stellar velocity dispersion may be not accurate. Figure 7 compares the best-fit spectra of ssSP and bsSP fittings with observed ones, and Figure 8 compares ssSP- and bsSP-fitted parameters. We find that both ssSP and bsSP models can be fitted to the spectra of eight galaxies, i.e., NGC 1399, NGC 1553, NGC 2865, NGC 3031, NGC 1404, NGC 221, NGC 1052, and NGC 205. At the same time, both bsSP and ssSP models do not fit the spectra with wavelengths larger than 6000 Å for NGC 210. This may result from the low upper metallicity (0.03) of our theoretical populations. In addition, we find that ssSPs can fit the observed spectra of NGC 1433 better than bsSPs. It seems that bsSPs fail to fit the observed spectra. This is possibly caused by the simple SFH used to build bsCSPs. Spiral galaxies possibly have more complicated SFHs, and bsCSPs with two components are not enough for studies of such galaxies. If bsCSPs with more components are used, the observed spectra can possibly be fitted better. The effect of different SFHs on population SEDs will be discussed later. Note that the result does not mean no binaries in galaxy NGC 1433, because the effects of many input parameters are degenerate.
Figure 7. Comparison of bsSP and ssSP-fitted SEDs with observational spectra of 10 galaxies. Black, red, and blue lines are for observed, bsSP-fitted, and ssSP-fitted spectra, respectively. All spectra are normalized at 5500 Å.
Download figure:
Standard image High-resolution imageFigure 8. Comparison of ssSP- and bsSP-fitted parameters of 10 galaxies. Filled circles denote spiral galaxy NGC 1433, and the others denote early-type galaxies. Solid lines are unity lines. log(M*)bs and log(M*)ss in panel (2,3) are bsSP- and ssSP-fitted stellar mass, respectively.
Download figure:
Standard image High-resolution imageTable 1. ssSP-fitted Parameters of 10 Galaxies
| Galaxy | Redshift | AV | Z | t1 | t2 | σ* | τV | 〈t*〉M | 〈t*〉L |
|---|---|---|---|---|---|---|---|---|---|
| NGC 1399 | 0.004753 | 0.0393 | 0.0263 ± 0.0015 | 13.55 ± 0.14 | 4.92 ± 6.59 | 237 ± 195 | 0.138 ± 0.097 | 13.38 ± 0.24 | 12.63 ± 0.61 |
| NGC 1553 | 0.004236 | 0.0468 | 0.0172 ± 0.0035 | 9.75 ± 1.65 | 2.40 ± 3.13 | 333 ± 44 | 0.143 ± 0.172 | 9.46 ± 1.76 | 8.42 ± 1.49 |
| NGC 2865 | 0.008619 | 0.1608 | 0.0172 ± 0.0040 | 10.18 ± 3.92 | 1.30 ± 0.85 | 350 ± 0 | 0.037 ± 0.050 | 9.90 ± 4.15 | 8.62 ± 3.75 |
| NGC 3031 | −0.000113 | 0.1486 | 0.0257 ± 0.0006 | 13.50 ± 0.00 | 0.82 ± 0.05 | 350 ± 0 | 0.382 ± 0.029 | 13.40 ± 0.00 | 12.19 ± 0.06 |
| NGC 1404 | 0.006391 | 0.0353 | 0.0205 ± 0.0036 | 13.45 ± 0.25 | 0.80 ± 0.16 | 314 ± 68 | 0.130 ± 0.128 | 13.35 ± 0.26 | 12.26 ± 0.11 |
| NGC 210 | 0.005457 | 0.0673 | 0.0160 ± 0.0061 | 6.68 ± 0.72 | 1.87 ± 0.23 | 342 ± 22 | 0.146 ± 0.183 | 6.20 ± 0.75 | 5.28 ± 0.80 |
| NGC 221 | −0.000667 | 0.4797 | 0.0113 ± 0.0074 | 11.25 ± 4.04 | 1.38 ± 0.20 | 350 ± 0 | 0.124 ± 0.197 | 11.02 ± 4.22 | 10.00 ± 4.57 |
| NGC 1433 | 0.003586 | 0.0282 | 0.0155 ± 0.0052 | 6.20 ± 0.00 | 3.78 ± 2.74 | 350 ± 0 | 0.102 ± 0.120 | 5.91 ± 0.26 | 5.46 ± 0.83 |
| NGC 1052 | 0.001004 | 0.0824 | 0.0200 ± 0.0000 | 13.60 ± 0.00 | 0.58 ± 0.05 | 350 ± 0 | 0.138 ± 0.024 | 13.51 ± 0.00 | 11.79 ± 0.15 |
| NGC 205 | −0.000777 | 0.1685 | 0.0122 ± 0.0005 | 6.20 ± 0.00 | 1.60 ± 0.00 | 307 ± 64 | 0.000 ± 0.000 | 5.70 ± 0.00 | 5.02 ± 0.01 |
Notes. The unit of t1, t2, 〈t*〉M and 〈t*〉L is Gyr, and that of σ* is km s−1. The values of redshift and AV are taken from NED.
Download table as: ASCIITypeset image
Table 2. bsSP-fitted Results of 10 Galaxies
| Galaxy | Redshift | AV | Z | t1 | t2 | σ* | τV | 〈t*〉M | 〈t*〉L |
|---|---|---|---|---|---|---|---|---|---|
| NGC 1399 | 0.004753 | 0.0393 | 0.0300 ± 0.0000 | 13.50 ± 0.00 | 12.27 ± 0.81 | 350 ± 0 | 0.182 ± 0.062 | 13.13 ± 0.20 | 13.10 ± 0.23 |
| NGC 1553 | 0.004236 | 0.0468 | 0.0183 ± 0.0069 | 11.87 ± 2.56 | 1.18 ± 0.19 | 348 ± 5 | 0.265 ± 0.090 | 11.69 ± 2.67 | 10.55 ± 2.93 |
| NGC 2865 | 0.008619 | 0.1608 | 0.0145 ± 0.0033 | 14.48 ± 0.30 | 0.68 ± 0.16 | 348 ± 5 | 0.043 ± 0.060 | 14.41 ± 0.31 | 12.98 ± 0.29 |
| NGC 3031 | −0.000113 | 0.1486 | 0.0230 ± 0.0000 | 12.80 ± 0.00 | 10.53 ± 0.97 | 350 ± 0 | 0.337 ± 0.019 | 12.29 ± 0.04 | 12.20 ± 0.11 |
| NGC 1404 | 0.006391 | 0.0353 | 0.0197 ± 0.0045 | 11.33 ± 0.45 | 3.25 ± 3.43 | 348 ± 5 | 0.232 ± 0.075 | 11.07 ± 0.52 | 10.33 ± 0.56 |
| NGC 210 | 0.005457 | 0.0673 | 0.0173 ± 0.0006 | 6.20 ± 0.00 | 5.95 ± 0.14 | 350 ± 0 | 0.235 ± 0.115 | 6.09 ± 0.06 | 6.09 ± 0.06 |
| NGC 221 | −0.000667 | 0.4797 | 0.0110 ± 0.0000 | 7.60 ± 0.00 | 4.43 ± 2.19 | 350 ± 0 | 0.165 ± 0.058 | 7.18 ± 0.19 | 6.85 ± 0.44 |
| NGC 1433 | 0.003586 | 0.0282 | 0.0172 ± 0.0043 | 6.67 ± 1.27 | 3.68 ± 3.01 | 350 ± 0 | 0.070 ± 0.097 | 6.44 ± 1.28 | 5.66 ± 0.71 |
| NGC 1052 | 0.001004 | 0.0824 | 0.0200 ± 0.0000 | 11.10 ± 0.00 | 11.10 ± 0.00 | 350 ± 0 | 0.000 ± 0.000 | 11.10 ± 0.00 | 11.10 ± 0.00 |
| NGC 205 | −0.000777 | 0.1685 | 0.0032 ± 0.0005 | 14.70 ± 0.49 | 0.20 ± 0.00 | 321 ± 51 | 0.013 ± 0.036 | 14.64 ± 0.50 | 9.95 ± 0.69 |
Note. Similar to Table 1 but for bsSP-fitted parameters.
Download table as: ASCIITypeset image
Figure 8 shows the comparison of ssSP and bsSP-fitted parameters of 10 galaxies. We see that ssSP and bsSP models report obviously different results for many parameters of early-type galaxies. In particular, the bsSP-fitted young-component ages (t2) of six early-type galaxies are significantly older than the ssSP-fitted results, and the bsSP-fitted dust extinctions (τv) of half the galaxies are obviously larger than the ssSP-fitted results. In addition, two kinds of stellar population models obtain different results for the mass-weighted, luminosity-weighted, and old-component ages of some galaxies. Furthermore, we see some difference between the bsSP- and ssSP-fitted stellar velocity dispersions (σ*). However, bsSP and ssSP models measure similar stellar metallicities and masses for most galaxies. We also see that two kinds of population models measure similar results for the spiral galaxy NGC 1433. This is because spiral galaxies usually contain many young stars, which are much more luminous than old binary stars. Only young stars can explain the observed spectra whatever models are used. As a result, similar results are derived from bsSP and ssSP models. When comparing the results of 10 real galaxies and 37 mock galaxies, we find good consistency: bsSP models measure older young-component ages and larger dust extinctions than ssSP models, while two types of models measure similar stellar metallicities and masses for galaxies. The reason is that binaries increase the UV flux, but dust decreases it. The more luminous the populations are, the higher dust extinction can be measured. Thus the inclusion of binaries in the population model leads to a higher dust extinction estimate. Because BS2fit can recover the ages of recent (t2 ⩽ 3.5 Gyr) star bursts well (see Figure 4), both tests of mock and real galaxies indicate that binary evolution affects the measurement of SFHs of early-type galaxies, significantly. This because old bsSPs are more luminous in the UV band than old ssSPs.
7. RESULTS FROM STAR CLUSTERS
In order to check the effects of binaries that are shown above, we use the average template spectra of GCs in the Galaxy, LMC, SMC, and Fornax to perform a similar study. Because the template spectra were built for population synthesis studies, they are suitable for our work. Another reason for using these data is that we do not have any more suitable UV–optical spectra for GCs on hand. These spectra were built from weighted sums of individual spectra of star clusters taking into account their spectral similarities, ages, and metallicities (Santos et al. 2002; Bonatto et al. 1995; Leitherer et al. 1996). They cover the UV spectral range observed with IUE and optical data from different ground-based telescopes (Leitherer et al. 1996). The spectra of GCs are divided into seven different groups (G2b, G2r, G3b, G3r, G4b, G4r, and G5) according to their metallicity and UV colors (Bonatto et al. 1995). While all groups have average ages older than 10 Gyr, the average metallicity of GCs decreases from the G2 to G5 groups. "b" and "r" denote blue and red colors in the UV band, respectively. Interestingly, out of five metal-rich GCs (G2 group: NGC 6388, NGC 6441, NGC 6624, M69, and 47Tuc), only 47Tuc does not exhibit UV-upturn. G3b and G4b groups have UV excess, while G3r and G4r do not show UV excess. The most metal-poor group, G5, does not have a strong far-UV flux. The reason for the different UV performance of the G3 and G4 groups is not clear and we try to answer it in this work. More detailed information of these groups can be found in Bonatto et al. (1995). Although there are seven groups of template spectra, only the G2 to G4 groups are studied in this work because the metallicity of G5 group is possibly poorer than the lower metallicity limit of theoretical populations.
When fitting the template spectra of GCs via the bsCSP and ssCSP models, the bsSP models show obvious advantages. Figure 9 shows the fittings of the average template spectra of the GCs. We find that the best bsCSP fits have lower χ2 values than the ssCSP fits, except for G4b, and the average χ2 of the best bsCSP fits is lower than that of the best ssCSP fits by 0.78. According to the χ2 values of best fits, we can conclude that bsCSPs fit to template spectra better than ssCSPs. It is also shown that the template spectra of G2 and G3 groups can be fitted well but those of G4 cannot. This possibly results from the inappropriate binary fraction of both the ssCSP (0%) and the bsCSP (50%) models. We can estimate from panel (2,3) of Figure 9 that the binary fraction of G4r is possibly between 0 and 50%. In addition, neither bsCSP nor ssCSP models fit some spectral parts, e.g., 4000 to 5000 Å. This may be caused by different synthesis processes of observed (each spectra is weighted by S/N when calculating average spectra) and theoretical (see Sections 2 and 3 for details) spectra. The fitted results of three groups are listed in Table 3, and a comparison of the bsCSP and ssCSP fitted results of these templates are shown in Figure 10. We find that bsCSP models measure larger t2 and τV values than ssCSP models on average, when we take only the reliable results (t2 ⩽ 3.5 Gyr and with small uncertainties) into account. The results are therefore inconsistent with those of early-type galaxies. When checking the property difference between red and blue subgroups of G3 and G4, bsCSP-fitted results show that blue subgroups (G3b and G4b) are relatively more metal-rich and older (t1) than red subgroups (G3r and G4r), while ssCSP-fitted results do not display such a trend. This suggests that the different UV spectra of blue (G3b and G4b) and red (G3r and G4r) subgroups are possibly caused by different stellar population properties, and that bsSP models are helpful for better understanding the spectra of star clusters.
Figure 9. Similar to Figure 7, but for the average template spectra of GCs.
Download figure:
Standard image High-resolution imageFigure 10. Similar to Figure 8, but for the fitted results of the average template spectra of GCs.
Download figure:
Standard image High-resolution imageTable 3. bsSP- and ssSP-fitted Results of Average Template Spectra of Globular Clusters from Our Galaxy, LMC, SMC, and Fornax
| Group |  |
fit type | Z | t1 | t2 | σ* | τV | 〈t*〉M | 〈t*〉L |
|---|---|---|---|---|---|---|---|---|---|
| G2b | 0.0063 | bsCSP | 0.0087 ± 0.0009 | 7.67 ± 0.09 | 1.57 ± 0.17 | 350 ± 0 | 0.173 ± 0.100 | 7.26 ± 0.66 | 6.00 ± 0.69 |
| G2b | 0.0063 | ssCSP | 0.0073 ± 0.0018 | 8.82 ± 2.61 | 1.57 ± 0.09 | 338 ± 33 | 0.103 ± 0.114 | 8.48 ± 2.77 | 7.27 ± 2.58 |
| G2r | 0.0040 | bsCSP | 0.0080 ± 0.0035 | 12.13 ± 4.59 | 4.10 ± 2.58 | 348 ± 5 | 0.123 ± 0.077 | 11.97 ± 4.65 | 11.50 ± 4.29 |
| G2r | 0.0040 | ssCSP | 0.0050 ± 0.0017 | 9.83 ± 2.01 | 4.35 ± 1.76 | 350 ± 0 | 0.223 ± 0.151 | 9.49 ± 2.07 | 9.09 ± 1.86 |
| G3b | 0.0012 | bsCSP | 0.0026 ± 0.0012 | 14.90 ± 0.12 | 2.73 ± 6.40 | 226 ± 194 | 0.219 ± 0.075 | 14.84 ± 0.14 | 12.82 ± 1.04 |
| G3b | 0.0012 | ssCSP | 0.0029 ± 0.0034 | 12.85 ± 5.47 | 2.92 ± 2.45 | 226 ± 195 | 0.148 ± 0.088 | 12.67 ± 5.59 | 12.17 ± 5.45 |
| G3r | 0.0011 | bsCSP | 0.0008 ± 0.0004 | 6.07 ± 0.11 | 4.87 ± 1.27 | 314 ± 83 | 0.367 ± 0.020 | 5.74 ± 0.28 | 5.64 ± 0.43 |
| G3r | 0.0011 | ssCSP | 0.0009 ± 0.0000 | 11.80 ± 0.69 | 1.72 ± 1.07 | 180 ± 67 | 0.73 ± 0.63 | 11.62 ± 0.67 | 10.63 ± 1.28 |
| G4b | <0.0010 | bsCSP | 0.0012 ± 0.0003 | 14.80 ± 0.10 | 5.15 ± 8.25 | 271 ± 153 | 0.223 ± 0.073 | 14.73 ± 0.10 | 12.98 ± 1.62 |
| G4b | <0.0010 | ssCSP | 0.0003 ± 0.0000 | 14.85 ± 0.14 | 8.82 ± 4.84 | 260 ± 164 | 0.209 ± 0.085 | 14.66 ± 0.09 | 14.44 ± 0.15 |
| G4r | <0.0010 | bsCSP | 0.0008 ± 0.0004 | 8.47 ± 4.24 | 5.05 ± 2.47 | 246 ± 181 | 0.347 ± 0.382 | 8.28 ± 4.19 | 7.89 ± 3.55 |
| G4r | <0.0010 | ssCSP | 0.0003 ± 0.0000 | 13.18 ± 1.07 | 1.10 ± 0.86 | 222 ± 167 | 1.016 ± 0.028 | 13.07 ± 1.09 | 11.69 ± 1.86 |
Notes. According to previous results based on ssSP models, all groups have average ages older than 10 Gyr.  means average metallicity. Meanings of other symbols are the same as Table 1.
means average metallicity. Meanings of other symbols are the same as Table 1.
Download table as: ASCIITypeset image
8. DEGENERATE EFFECTS OF BINARY FRACTION AND POPULATION AGE ON SEDs
The above sections show that the spectra of early-type galaxies and star cluster groups can be explained using both old bsCSPs and young ssCSPs. This implies that old binaries and young single stars should have similar effects on the spectra of populations. We study the effects of these two factors in this section, in order to understand better the reason for different results from bsCSP and ssCSP models. The results are shown in Figure 11. As we can see, binary fraction and stellar age have degenerate effects on the SEDs of stellar populations. Both decreasing stellar age and increasing binary fraction can lead to UV-upturn. This explains why bsCSP and ssCSP models can be fitted to the observed spectra but the results are different. In addition, the change in binary fraction and stellar age can affect the shape of optical spectra, but stellar age affects it much more significantly than binary fraction. This suggests that optical spectra have strong constraints on the age of populations, while UV spectra have them on binary fractions. In addition, binary separation also affects the spectra. Because smaller binary separations mean more close binaries in a population, a change of binary separation should be able to be expressed by a change in binary fraction, roughly. We therefore do not perform a similar experiment on binary separation. One can use Figure 11 to obtain an image of how binary separation affects the SEDs of populations.
Figure 11. Degenerate effects of binary fraction and age on SEDs of stellar populations. Black lines are for some bsSSPs with a fixed binary fraction (50%) but various ages, while color lines are for populations with the same main population parameters (metallicity and age) but various binary fractions. The meanings of different types of lines are shown in the figure.
Download figure:
Standard image High-resolution image9. CONCLUSION AND DISCUSSION
This paper investigates the potential importance of binary evolution in the UV–optical spectral fitting of early-type galaxies via a new spectral fitting code (BS2fit). The result shows that optical spectra are important for constraining stellar age and UV spectra are important for constraining binary fraction. The results of both mock and real galaxies show that stellar population models including binary evolution will provide different estimates for galaxy parameters such as young-component age and dust extinction.
The difference between bsSP- and ssSP-fitted young-component ages (t2) can be as large as 7 Gyr (mock galaxies) or 10 Gyr (real galaxies), while the optical depth (τV) can be different by about 0.15 if ssSP-fitted τV is low (<0.25). Our results suggest that binary evolution can possibly play an important role in the spectral fitting of early-type galaxies, while it may be not so important for spiral galaxies. It is therefore necessary to take binaries into account in spectral synthesis studies. Because the stars of most galaxies are possibly formed in more than one star burst, and SFHs supply unique information for studying galaxy formation and evolution, it is crucial to include the effects of binaries in stellar population models when studying the SFHs of galaxies. In addition, this study shows that bsSP models measure larger optical depth for galactic dust because bsSPs are more luminous than ssSPs in UV band. This is possibly helpful for explaining why negative extinction values are needed in some spectral fittings based on ssSP models (e.g., Cid Fernandes et al. 2005). The conclusion derived from early-type galaxies is also supported by the study of template spectra of Galactic GCs.
Furthermore, although parameters such as old-component age and stellar velocity dispersion, which are derived from bsSP and ssSP models, are roughly consistent, the results for some specific galaxies are very different (e.g., 8 Gyr for t1 and 100 km s−1 for σ*). This implies that binary evolution may affect more studies about galaxies. Moreover, the bsSP-fitted results of GC template spectra show that the main population parameters (metallicity and age) of the UV-blue and red subgroups of G3 and G4 are different, which is not shown by ssSP-fittings. This suggests that bsSP models are helpful for explaining the UV spectra difference of UV-blue and red subgroups of median-metallicity GCs.
This work is only a simple test of the effects of binaries. It should be improved on in the future. First, a fixed binary fraction (50%) is used for all bsSPs, although the real fraction may be different from one galaxy to another. However, our results are potentially useful, because 50% is a typical binary fraction of our Galaxy, and this fraction can fit the spectra of most galaxies. In addition, the assumption of the separation of binary components may have obvious effects on the final results, although other adjustable parameters slightly affect the results (Hurley et al. 2002; Li et al. 2012a). Another disadvantage of this work is the generation of the star sample. Because the masses of the secondary components of the binaries are calculated from those of the primary components, it leads to more low-mass stars than the prediction of selected IMF. This will lead to some uncertainties in the results if these models are used to study galaxies and star clusters. Therefore, although the main results of this work may not be affected too much, theoretical stellar populations should be rebuilt based on the new results of IMF studies. On the other hand, although it is possible that UV-upturn is caused mainly by binary evolution, some single extreme horizontal branch stars can also affect the UV flux of early-type galaxies (e.g., Brown et al. 2000) and then the final results. Thus our results actually show the maximum effects of binaries on the spectral fittings of early-type galaxies. Moreover, a simple assumption for SFH was used to model the CSPs of early-type galaxies. This is possibly reasonable for most early-type galaxies, but more complicated SFHs may be needed for some galaxies, in particular late-type ones. As we see in Figure 7, there is an obvious difference between the observational and best bsSP fit spectra for NGC 1433. This possibly results from the simple SFH of bsCSPs, because spiral galaxies usually contain more than two population components and the model of this work is not enough to express the stellar population properties of such galaxies. If we want to fit the observed spectra better, bsCSPs that contain more components are needed. Via Figure 12, we test the effect of different SFHs on the SEDs of bsCSPs, which shows that the inclusion of more population components will make populations more luminous toward the near-infrared and a little less luminous toward the blue band (3000–5000 Å). This explains why the spectra of NGC 1433 is not fitted well by bsCSPs containing only two components (see Figure 7). The result suggests that bsCSPs with more components are needed for studies of late-type galaxies, e.g., NGC 1433. Note that when bsCSPs with more components are used, larger τV values will be obtained, and it makes the result more natural as spiral galaxies usually contain more dust than early-type galaxies (Smith et al. 2012). In fact, the exponential decline SFH still contains some uncertainties, which can affect the results significantly.
Figure 12. Effect of SFHs on SEDs of populations. Dashed, dotted, and solid lines show SEDs of populations that contain two, three, and six components, respectively. The mass fractions of different components are assumed to decline exponentially with decreasing stellar age.
Download figure:
Standard image High-resolution imageAs a whole, the effects of various factors such as binary separation, binary fraction, population age, dust attenuation, metallicity, and SFH are degenerate. A series works of detailed studies on the degeneracy of these factors will help us to understand the role of binaries. Besides these, the stellar masses of populations were measured by the flux at 5500 Å in this work. If stellar mass is determined at other wavelengths, e.g., 4000 Å, the bsSP- and ssSP-fitted stellar masses may be more different. Finally, we used a rapid spectral fitting technique in the BS2fit code because of the limitation of our computation ability. This leads to some uncertainties in the results. Although this does not affect the results of this work too much, it is necessary to make the code more accurate and check the results again.
We thank the referee for detailed comments and acknowledge Professors Pavel Kroupa, Xiangdong Li, Qiusheng Gu, and Shiyin Shen for suggestions and discussions. This work is supported by Chinese National Science Foundation (grant Nos. 10963001 and 11203005), Yunnan Science Foundation (2009CD093), and Chinese Postdoctral Science Foundation. We also thank the support of the Sino-German Center (GZ585) and the K. C. Wong Education Foundation.
Footnotes
- 4
The code and data can be obtained on request to Zhongmu Li, and the authors are trying to make it available on the Internet.
- 5














