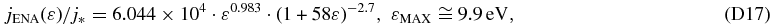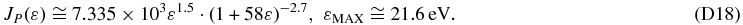ABSTRACT
We develop a physical model to study the pressure of the source proton plasma in the inner heliosheath based on the IBEX Energetic Neutral Atom (ENA) spectra. A multiple linear regression technique is used to parameterize the proton distribution function, by connecting the observed ENA flux spectrum from IBEX-Hi with the power-law of the model proton distribution. We calculate the partial pressure over the measured energy range, using (1) a non-parametric method by integrating the observed ENA flux, and (2) a parametric method by integrating the modeled distribution of protons in the inner heliosheath. The two sky maps of the parametric and non-parametric partial pressures are nearly identical, owing to their power-law distributions at high energies; the kappa distribution is such a function that can be reduced to a power-law in the IBEX-Hi energy range. The slight differences between the two partial pressures may indicate protons that are not described by the kappa distribution, and instead, involve newer or "immature" (spherical shell) pick-up proton distributions. Ultimately, however, these become incorporated with the solar wind into one single proton population described by a kappa distribution. Moreover, we derive analytically (1) the ENA flux spectra, which suggests that this flux maximizes at ∼30 eV, and (2) the differential pressure, which provides estimates of the partial pressures outside of those measured by IBEX-Hi. Under the assumptions of the modeled ENA spectra, the Ribbon emissions appear to be primarily limited to the energy ranges of IBEX-Lo and IBEX-Hi.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
The Interstellar Boundary Explorer (IBEX; McComas et al. 2009a) was launched on 2008 October with the primary objective to observe emissions of energetic neutral atoms (ENAs) from the outer heliosphere, where the subsonic solar wind interacts with the interstellar medium. IBEX made the first observations of ENAs from the outer heliosphere and revealed a narrow "Ribbon" of emissions encircling the sky, up to two to three times brighter than the broad emissions of the globally distributed ENA flux (McComas et al. 2009b; Funsten et al. 2009; Fuselier et al. 2009; Schwadron et al. 2009).
IBEX images the sky via two ultra-sensitive ENA detectors (IBEX-Hi, IBEX-Lo) and constructs 60 × 60 all-sky maps every ∼6 months, covering a broad energy range from ∼0.01 to ∼6 keV. Here we use data from the IBEX-Hi sensor with energies of 0.5–6 keV FWHM from the first year of IBEX observations (McComas et al. 2010), as was done in several other previous studies (e.g., Dayeh et al. 2011; Schwadron et al. 2011; Livadiotis et al. 2011, 2012; Livadiotis & McComas 2012a).
Using the IBEX-Hi energy-flux ENA spectra, Livadiotis et al. (2011) derived the sky maps of the source proton average thermal observables in the inner heliosheath. This was enabled by connecting the observed ENA flux to the parametric distribution of velocities of the source protons.
In particular, we used a kappa distribution to parameterize the proton distribution because it (1) well describes the space plasmas throughout the heliosphere (Livadiotis & McComas 2009; Livadiotis et al. 2012 and references therein); (2) has a strong foundation in non-extensive statistical mechanics (Livadiotis & McComas 2009), leading to a consistent definition of temperature and pressure for systems residing in stationary states out of thermal equilibrium (Livadiotis & McComas 2010a, 2012a); and (3) is consistent with the expected and observed power-law behavior of ENA spectra (Livadiotis & McComas 2009, 2010a; Livadiotis et al. 2011).
The kappa index, κ, which characterizes the kappa distribution, is an independent thermodynamic variable that plays a key role in describing the governing thermodynamic processes in space plasmas (Livadiotis & McComas 2012a). The significance of κ is primarily given by its role in identifying the non-equilibrium stationary states; the smaller the κ, the further from equilibrium the system resides. The classical, single stationary state at equilibrium is thus generalized into a whole set of different non-equilibrium stationary states, each labeled by a separate value of the kappa index, and collectively producing the κ-spectrum (Livadiotis & McComas 2010b, 2010c, 2012b). The kappa index provides a suitable measure of the "thermodynamic distance" of stationary states from thermal equilibrium (Livadiotis & McComas 2010a, 2010c, 2011b), while its physical meaning is connected to the correlation between the system's particles (Livadiotis & McComas 2011b).
In this study, we seek to characterize the "dominant" source along each line of sight (LoS), which provides the bulk of the ENAs observed in that pixel. This dominant source proton distribution is inferred from the ENA flux maps and uniquely enables estimation of the relevant thermodynamic parameters of the protons that are the primary constituent of the source plasma. These are specifically the kappa index κ, the temperature T, the density n, and the pressure P, which are shown here with bars to indicate that they represent emission region averages along each observed LoS. Moreover, instead of applying a direct nonlinear regression to fit the kappa distribution, Livadiotis et al. (2011) demonstrated a more accurate method of multiple linear regression on the power-law spectra. Through this, the observed power-law of the ENA flux spectra can be analytically connected to the kappa distribution of the dominant emitting source protons, which also behaves asymptotically at high energies as a power-law. In fact, four conditions must be fulfilled in order for the ENA flux spectra to be described by a power-law; these are described in Section 2.
The multiple linear regression processing connects the power-law spectrum of the observed ENAs and the parameterized power-law distribution of the source plasma ions over the energy range of the observations. First, we apply a linear regression to the ENA flux spectrum using the simple expression log jENA(ε) = log j*–γ log ε, from which the spectral index, γ (≈κ), and the logarithm of the ENA flux at 1 keV, log j*, are derived. The first applied fitting derives one pair of (γ, log j*) values. However, a number of such pairs is needed for the second fitting. Using the technique described in Appendix A, we generate a number of such pairs. The second applied fitting is a multiple linear regression to the ensemble of the derived pairs of (γ, log j*) values. The slope and intercept of the second linear regression yields estimates of the radially averaged temperature T and density n, respectively, of the source plasma. Using this methodology, we derive the triplet of (κ, T, n) values for each of the IBEX ENA flux spectra and over different viewing directions. In this way, the sky maps of (κ, T, n) were constructed (Livadiotis et al. 2011), while the involved thermodynamic processes were explored (Livadiotis & McComas 2012a), for the first year of the IBEX observations (McComas et al. 2010).
One of the most important aspects of the above analysis was the parametric derivation of the thermal pressure P = nkBT (kB: Boltzmann's constant; Livadiotis & McComas 2012a). Even though the analysis used the observations over the finite energy range of IBEX-Hi data (Funsten et al. 2009b), it derives a total pressure that characterizes the entire proton energy distribution. This derivation is obtained through extrapolation based on the physical processes and fundamental plasma properties that underlie the values of (κ, T, n) derived over the limited energy range of IBEX. Hence, we assume that the entire distribution over all energies can be given by a single kappa distribution function as parameterized by the data analysis over the IBEX-Hi energy range.
We additionally utilize a different approach in which partial pressures measured over a limited number of discrete energy passbands resulting in a fixed energy range can be extracted directly from the ENA flux, without assuming a parameterized thermodynamic function (Funsten et al. 2009a; Roelof et al. 2010, 2012; Schwadron et al. 2011). This non-parametric, empirical pressure is expected to be smaller than the parametric pressure nkBT, since the former integrates the flux over the finite IBEX-Hi energy range, while the latter is analytically derived from integrating the entire extrapolated distribution over all the energies (0 < ε < ∞).
Moreover, the partial parametric pressure can be derived from integration of the proton kappa distribution over the same finite interval of the IBEX-Hi energy range. Then, the partial non-parametric pressure can be directly compared with the partial parametric pressure over an identical energy range. The constructed sky maps of the (parametric and non-parametric) partial pressures are expected to be similar; in fact, we show that if the source proton distribution is a power-law, then the two will be identical. Here we use the kappa distribution, which is reduced to a power-law at high energies.
In this paper, we show for the source proton plasma in the inner heliosheath (1) the sky maps of both the parametric and non-parametric partial pressures are almost identical, supporting the concept that the dominant proton plasma in the source region is well described by a power-law at higher energies, which is a behavior consistent with the kappa distributions; (2) the slight differences between these two partial pressures could be attributed to the influence of the distribution of newly formed pick-up ions (PUIs) and/or the bimodal structure of solar wind on the ENA flux spectra; (3) the matured pick-up protons are ultimately incorporated into the proton plasma of the inner heliosheath; this is statistically described by a single proton population following a kappa distribution, common for solar wind and matured pick-up protons; (4) analytical derivation of the function of the ENA energy-flux spectra, which suggests that the maximum flux is at energy ∼30 eV; and (5) the partial pressure over energy intervals other than the IBEX-Hi range, where the Ribbon appears primarily between ∼30 eV and 6 keV, the energy range largely covered by the IBEX-Hi and -Lo.
We organize the paper as follows. In Section 2, we briefly explain the multiple linear regression technique using ENA flux spectra to find the thermodynamic values of (κ, n, T, P) for most directions in the sky. In Section 3, we derive and compare the (total and partial) parametric and the partial non-parametric pressures. In Section 4, we derive and qualify the distribution of pressure in energy-flux spectra. Then, in Section 5, we discuss (1) the effect of PUI distribution on the IBEX-Hi ENA flux spectra; (2) the PUI contribution in the pressure of the inner heliosheath; the incorporated solar wind and pick-up protons described by a common kappa distribution; and (3) the partial and total pressure that is related to the globally distributed flux. Finally, Section 6 summarizes the conclusions, while Appendices A–D provide proofs of the pressure equations used in this paper.
2. THE MULTIPLE LINEAR REGRESSION TECHNIQUE
The flux jENA of ENAs that are generated by a proton–hydrogen charge exchange at a heliocentric distance r and measured by IBEX (located at r = 1 AU), is given by the LoS integral (Gruntman 1992),
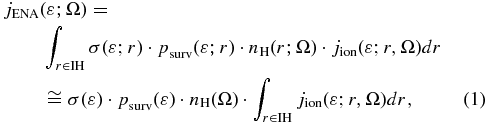
where ε is the energy of ENAs in the inertial reference frame of the heliosphere. Because the average energy transfer between atoms in a charge exchange collision is miniscule and we expect that the bulk proton flow of the source plasma is small compared to its thermal motion, ε is representative of the kinetic energy of the source protons in its own reference frame. We note that the IBEX spacecraft velocity is also comparatively small, however, we use Compton-Getting corrected data anyway (McComas et al. 2010). Thus, ε represents also the proton energy in the spacecraft frame.
In Equation (1), the cold, interstellar neutral hydrogen density has weak dependence on r in the inner heliosheath, nH(r, Ω)≅nH(Ω); jion(ε; r, Ω) is the flux of the source protons; and the solid angle Ω denotes in a compact way both the heliographic latitude ϑ and longitude φ of the ENA sky maps as viewed from the inner heliosphere; σ(ε) is the proton–hydrogen charge exchange cross section. The survival probability psurv(ε) of an ENA along its trajectory from its source to its measurement at IBEX includes ionization via charge exchange, electron impact ionization, and photoionization and its radial variation is significant only in the inner heliosphere inside a heliocentric distance of r ∼ 5 AU. The observed ENA flux in Equation (1) represents the line-of-sight integration of ENA emission over the inner heliosheath thickness (r ∈ IH).
For most directions Ω, most of the ENAs observed by IBEX are almost certainly generated in the inner heliosheath (e.g., Zank 1999; McComas et al. 2009c). In fact, Livadiotis et al. (2011) found that most heliospheric ENAs detected by IBEX are associated with proton source of typically high-temperature values (T ∼ 106 K) and low kappa values (κ < 2.5), which are similar to model predictions for the inner heliosheath proton plasma (Heerikhuisen et al. 2008; Livadiotis & McComas 2010a, 2010c). Therefore, they supported the idea that the dominant proton source of primary ENAs is likely located in the inner heliosheath. We note though that the proton plasma in the inner heliosheath may be the dominant, but certainly not the unique, source of primary ENAs that are detected by IBEX. Indeed, the only requirement for an ENA to reach IBEX is that the velocity (bulk and thermal) of the parent proton will allow it (Gruntman et al. 2001, cf. Figure 5).
While the globally distributed flux emissions are thought to be of primary ENAs (e.g., Schwadron et al. 2011), and thus coming from the inner heliosheath, the IBEX Ribbon could be generated by a variety of processes in the outer heliosphere, including a secondary ENA process with the original source protons coming from inside the heliosphere, and directly from neutralization of the supersonic solar wind (McComas et al 2009b, 2010, 2012; Heerikhuisen et al. 2010; Chalov et al. 2010), or/and of the hot inner heliosheath (Zank et al. 1996; G. P. Zank 2012, private communication).
The Ribbon ENAs have to be statistically described by the superposition of two kappa distributions, corresponding to the two original source proton populations. However, the supersonic solar wind protons are characterized by larger kappa indices associated with near-equilibrium stationary states (Livadiotis & McComas 2010a, 2010c, 2012b), which generate ENAs of steeper spectra. At higher energies the contribution of the steeper spectra of the supersonic solar wind protons can be negligible compared to the flattener spectra of the inner heliosheath protons. Hence, we can still manipulate the Ribbon ENAs using a single kappa distribution to describe the original source protons of the inner heliosheath.
Most of the observed ENA energy-flux spectra at low- to mid-latitudes are well described by a power-law, i.e., ∂log jENA/∂log ε ∼ constant, within measurement uncertainties and characterized by a single spectral index κ (e.g., see McComas et al. 2009b). How can this be explained within the intrinsic complexity of multiple energy-dependent processes and LoS contributions that are essential ingredients of Equation (1)? First, there is an approximate cancellation between the energy dependence of the charge exchange cross section and the survival probability over the IBEX-Hi energy range. Livadiotis et al. (2011) showed that σ(ε) · psurv(ε) = σ0p0 · (ε/1 keV)−b with σ0p0≅(1.77 ± 0.15) × 10−15(cm2) and a very small power exponent b≅0.017 ± 0.016 compared to the spectral power index of the source proton distribution. Then, it follows from Equation (1) that if jENA(ε; Ω) is characterized by energy power-law, then a power-law should also hold for jion (ε; r, Ω).
Overall, four main conditions must be fulfilled for the ENA flux to be described by power-law: (1) the energy dependence of the charge exchange cross section and the survival probability must be approximated by a power-law in the energy range of interest (as described above); (2) the source protons must be in a single stationary state described by a single kappa distribution and not by a superposition of kappa distributions with different κ-indices; (3) this stationary state remains approximately constant (fixed κ-index) along the integration column of the ENA flux, and (4) the source protons must be sufficiently energetic to reach the high-energy asymptotic statistical behavior of a kappa distribution; at that limit, the thermal energy dominates the bulk flow energy, as is generally expected in the inner heliosheath. (Livadiotis et al. 2011 explained and supported these conditions in detail.) If all these conditions are met, then the ENA energy-flux relation is a power-law, written as
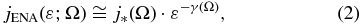
where the spectral index, γ, and the 1 keV flux, j*, are connected to thermodynamic variables of the source proton plasma, i.e.,
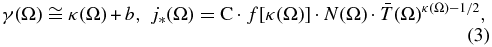
with the constant given by C≅(1.04 ± 0.08) × 105 cm3 s−1 sr−1 keV−1 (Equation (B10)); the flux is expressed in cm−2 s−1 sr−1 keV−1, the densities in cm−3, and the temperature in keV/kB≅11.6 × MK. The function f(κ) ≡ (κ − 3/2)κ − 1/2Γ(κ + 1)/Γ(κ − 1/2) (Equation (C7)) is derived from the kappa distribution asymptotic behavior at high energies, ε ≫ (κ − 3/2)kBT (see Equation (D4)).
The 1 keV flux, j*, is expressed by the integral j* = C · f(κ) · ∫r ∈ IHnH(r) · n(r) · T(r)κ − 1/2dr that gives the average value of the integrand nH(r) · n(r) · T(r)κ − 1/2 along the heliocentric distance r. As before, n is the density of the protons in the source plasma. The density factor N(Ω) is defined by
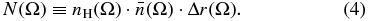
The mean-value bar denotes the radial averaging over the inner heliosheath thickness Δr(Ω) along the LoS at direction Ω. This radial averaging aims to attribute a representative value to several thermal parameters that have some weak dependence on r over the source region.
ENAs observed by IBEX from the inner heliosheath (and outer heliosheath if some come from there) represent integrations along the LoS from source regions that could have vastly different thermodynamic properties. In this case, the source proton populations cannot be represented by a single dominant kappa distribution and the data analysis technique (Appendix A) cannot be applied. This failure exists for the suppressed (black) pixels in the sky maps of Figure 1, and ultimately, the ability of a single kappa distribution to fit the IBEX ENA observations comes down to the statistical accuracy in each pixel. In fact, the goodness of the fitting may be satisfactory for pixels with high uncertainties, and the least accurate pixels in the sky maps end up being fit through our current technique. The sky maps of the thermal observables can be qualitatively characterized by being compared to the sky maps of the time exposure (e.g., see Figure 1 in Livadiotis et al. 2011). The Ribbon and the globally distributed flux emissions can be associated with different source distribution functions because of different values of their thermal parameters (kappa index, temperature, density). In each pixel, our technique is driven by the dominant of these two source distributions, except where they have similar contributions to the total emission. In this case, the technique can (1) either fail retaining a black pixel, that is when the two distributions have different spectral behavior (e.g., forming an ankle or a knee), or, (2) result in some sort of averaging the thermal parameters by handling the total distribution as one single kappa distribution, that is when the two distributions have similar spectra.
Figure 1. Sky maps of (a) the ENA flux  averaged over the IBEX-Hi energy range (shown for reference), (b) kappa index κ, and the radial averages of the (c) temperature
averaged over the IBEX-Hi energy range (shown for reference), (b) kappa index κ, and the radial averages of the (c) temperature  , (d) density
, (d) density  , and (e) pressure
, and (e) pressure  , of the source protons in the inner heliosheath. The analysis of Livadiotis et al. (2011) provided an estimation of κ,
, of the source protons in the inner heliosheath. The analysis of Livadiotis et al. (2011) provided an estimation of κ,  , N, and the construction of their sky maps. Additional model analysis helped to separate the proton density
, N, and the construction of their sky maps. Additional model analysis helped to separate the proton density  and the inner heliosheath thickness Δr from the density factor N (Equation (4)), while the pressure
and the inner heliosheath thickness Δr from the density factor N (Equation (4)), while the pressure  was calculated using Equation (7). Note that the black pixels denote ENA spectra that are not well described by power-law, and thus, the multiple linear technique using a single kappa distribution cannot be applied. This holds for all the presented sky maps in this analysis. (Each point of the map corresponds to a 60 × 60 pixel. The directions toward the heliospheric Nose (N), and Voyager' spacecraft (V1 and V2) are indicated in every sky map of this paper.)
was calculated using Equation (7). Note that the black pixels denote ENA spectra that are not well described by power-law, and thus, the multiple linear technique using a single kappa distribution cannot be applied. This holds for all the presented sky maps in this analysis. (Each point of the map corresponds to a 60 × 60 pixel. The directions toward the heliospheric Nose (N), and Voyager' spacecraft (V1 and V2) are indicated in every sky map of this paper.)
Download figure:
Standard image High-resolution imageThe second linear regression needs a modified value of the 1 keV flux j*, called "reflected" 1 keV flux, that is defined by  and approximately equal to
and approximately equal to
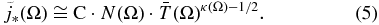
In particular, the first linear regression on the values of (log ε, log jENA) involves finding the pair of (log j*, γ) for each of the 1800 pixels in a 6º × 6º sky map, along a LoS direction Ω from IBEX. Then, the second linear regression on the values of (κ − 1/2, log  ) derives the desired pair of values (logN, log
) derives the desired pair of values (logN, log  ). However, the first fitting yields only one pair of (log j*, γ), while a number of such pairs is needed for the second fitting. A special technique is employed for generating such pairs within the standard deviation of their mean values. This technique is called "variation of fitting parameters" and it is discussed further in Appendix A. It generates a number ν of input pairs (xi, yi), i = 1, ..., ν, with (x ≡ κ − 1/2,
). However, the first fitting yields only one pair of (log j*, γ), while a number of such pairs is needed for the second fitting. A special technique is employed for generating such pairs within the standard deviation of their mean values. This technique is called "variation of fitting parameters" and it is discussed further in Appendix A. It generates a number ν of input pairs (xi, yi), i = 1, ..., ν, with (x ≡ κ − 1/2,  ), where each of these values is included within the 1σ interval x − δx ⩽ xi ⩽ x + δx, y − δy ⩽ yi ⩽ y + δy, ∀i = 1, ..., ν.
), where each of these values is included within the 1σ interval x − δx ⩽ xi ⩽ x + δx, y − δy ⩽ yi ⩽ y + δy, ∀i = 1, ..., ν.
3. PARAMETRIC AND NON-PARAMETRIC THERMAL PRESSURE
3.1. Parametric Derivation of Thermal Pressure via Thermal Observables
Livadiotis et al. (2011) showed that the density factor N(Ω) can be connected to the ion density as  with constant c calculated for the values near the nose (N),
with constant c calculated for the values near the nose (N),  . The average densities are
. The average densities are  cm−3 and
cm−3 and  cm−3, while the inner heliosheath thickness is about Δr(ΩN)≅50 ± 5 AU. (For all the previous values, see, for example, Richardson & Stone 2009; Chalov et al. 2004). Thus, the density can be derived from the density factor,
cm−3, while the inner heliosheath thickness is about Δr(ΩN)≅50 ± 5 AU. (For all the previous values, see, for example, Richardson & Stone 2009; Chalov et al. 2004). Thus, the density can be derived from the density factor,  , or more precisely,
, or more precisely,
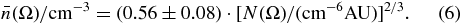
The ion thermal pressure is given by
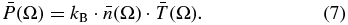
In practice, we calculate pressure using Equation (7) as follows: first, the fitting of Equation (2) between the ENA energy ε and the flux jENA involves finding the kappa index κ, the 1 keV flux j*, and its "reflected" value  . Then, the fitting of Equation (5) between (κ − 1/2) and
. Then, the fitting of Equation (5) between (κ − 1/2) and  leads to the density factor N and temperature
leads to the density factor N and temperature  , where N gives the ion density
, where N gives the ion density  via Equation (6). Finally,
via Equation (6). Finally,  and
and  lead to an estimation of the thermal pressure
lead to an estimation of the thermal pressure  via Equation (7). In this way, we are able to derive the thermal observables κ(Ω),
via Equation (7). In this way, we are able to derive the thermal observables κ(Ω),  ,
,  , and
, and  . Figure 1 shows the sky maps of these parameters at the standard IBEX 60 × 60 pixel resolution (McComas et al. 2010).
. Figure 1 shows the sky maps of these parameters at the standard IBEX 60 × 60 pixel resolution (McComas et al. 2010).
We observe that the Ribbon is also visible in all the sky maps of thermal observables; however, it is most prominent in the sky map of pressure. Both the Ribbon and the globally distributed flux are governed by isobaric thermodynamic processes; the pressure is quasi-constant,  within the Ribbon and
within the Ribbon and  for the globally distributed flux (Livadiotis & McComas 2012a). Indeed, the pressure sky map gives a clear distinction of the Ribbon from the global distribution.
for the globally distributed flux (Livadiotis & McComas 2012a). Indeed, the pressure sky map gives a clear distinction of the Ribbon from the global distribution.
3.2. Non-parametric Derivation of Pressure via Flux Integration
We described above how the quadruplet of thermodynamic parameters (κ, n, T, P) that characterize the thermodynamic processes can be derived from the IBEX-Hi ENA flux spectra. Note that the pressure in Figure 1(e) represents that produced over all energies (0 < ε < ∞) of the proton distribution. However, there is an independent approach, in which partial pressures measured over different (finite) energy ranges can be extracted directly from the ENA flux, without assuming a parameterized thermodynamic function (e.g., Funsten et al. 2009a; Roelof et al. 2010, 2012; Schwadron et al. 2011).
Consider the pressure  that can be derived directly from the ENA flux integration (Appendix B),
that can be derived directly from the ENA flux integration (Appendix B),
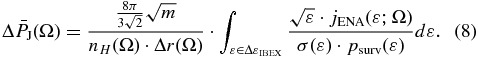
Ideally, the integration in Equation (8) would be over the whole energy spectrum ε ∈ [0, ∞). However, the ENA flux is measured over a finite range—in this case the IBEX-Hi energy range (ε ∈ ΔεIBEX), and the pressure is only partially measured. Note that this method cannot give the sky map of the pressure  (Ω) unless we know the dependence of hydrogen density nH and thickness Δr as functions of the direction Ω in the inner heliosheath.
(Ω) unless we know the dependence of hydrogen density nH and thickness Δr as functions of the direction Ω in the inner heliosheath.
The ratio of pressures  is given by dividing Equation (8) with the total pressure given in Equation (7), written as
is given by dividing Equation (8) with the total pressure given in Equation (7), written as ![$\bar P_{\rm T} (\Omega) = k_{\rm B} \bar T(\Omega) \cdot N(\Omega)/[n_{\rm H} (\Omega) \cdot \Delta r(\Omega)]$](https://content.cld.iop.org/journals/0004-637X/762/2/134/revision1/apj453971ieqn63.gif) (by combining Equations (4) and (7)), that is
(by combining Equations (4) and (7)), that is
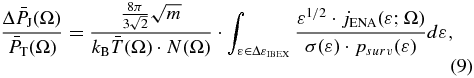
where we denoted with PT the pressure that is derived from thermal observables (as shown in Equation (7)).
In Appendix B, we show that Equations (8) and (9) can be written as
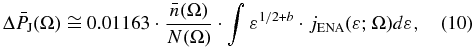
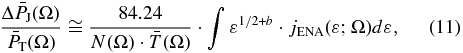
where the pressures are in pdyn cm-2, the density factor N in cm-6 AU, the density n in cm-3, the energy ε in keV, the flux jENA in cm−2 s−1 sr−1 keV−1, and the temperature T in K.
The inner heliosheath pressures  (Equation (8)) and
(Equation (8)) and  (Equation (7)) are calculated for each LoS direction Ω, and their pressure sky maps are depicted in Figure 2, (a)
(Equation (7)) are calculated for each LoS direction Ω, and their pressure sky maps are depicted in Figure 2, (a)  , (b)
, (b)  , (c)
, (c)  /
/ , with their histograms given in panels (d), (e), and (f), respectively. The values of
, with their histograms given in panels (d), (e), and (f), respectively. The values of  , given by ENA-flux integration, are by definition smaller than the pressure
, given by ENA-flux integration, are by definition smaller than the pressure  values; the most frequent values are
values; the most frequent values are  ∼ 2.1 pdyn cm−2 and
∼ 2.1 pdyn cm−2 and  ∼ 0.6 pdyn cm−2 with difference ∼1.5 pdyn cm−2 (Figures 2(d) and (e)), and ratio
∼ 0.6 pdyn cm−2 with difference ∼1.5 pdyn cm−2 (Figures 2(d) and (e)), and ratio  /
/ ∼ 0.3 (Figure 2(f)). The lower pressure values
∼ 0.3 (Figure 2(f)). The lower pressure values  compared to those of
compared to those of  are expected since the IBEX-Hi measurements span a finite energy range that lies above the energy of the maximum of the distribution. We also note that the Ribbon appears as a smooth and clear structure in pressure's sky map (Figure 2(a)) similar to ENA flux map (Figure 1(a)); in contrast, the Ribbon appears noisy in the partial pressure
are expected since the IBEX-Hi measurements span a finite energy range that lies above the energy of the maximum of the distribution. We also note that the Ribbon appears as a smooth and clear structure in pressure's sky map (Figure 2(a)) similar to ENA flux map (Figure 1(a)); in contrast, the Ribbon appears noisy in the partial pressure  map (Figure 2(b)).
map (Figure 2(b)).
Figure 2. Estimation of pressure by (1) using thermal observables,  (parametric pressure), and (2) integrating the ENA flux,
(parametric pressure), and (2) integrating the ENA flux,  (non-parametric pressure). Panels (a)–(c) show the sky maps, and (d)–(f) the histograms of
(non-parametric pressure). Panels (a)–(c) show the sky maps, and (d)–(f) the histograms of  ,
,  and their ratio
and their ratio  /
/ , respectively. The most frequent pressure values are
, respectively. The most frequent pressure values are  ∼ 2.1 pdyn cm−2,
∼ 2.1 pdyn cm−2,  ∼ 0.6 pdyn cm−2, and the ratio,
∼ 0.6 pdyn cm−2, and the ratio,  /
/ ∼ 0.3. As expected, the partial pressure values
∼ 0.3. As expected, the partial pressure values  are smaller (∼1.5 pdyn cm−2 on average) than the total pressure values,
are smaller (∼1.5 pdyn cm−2 on average) than the total pressure values,  .
.
Download figure:
Standard image High-resolution imageA number of limitations characterize the non-parametric pressure  when compared to the parametric pressure
when compared to the parametric pressure  . (1) Pressure underestimation: as previously explained, the integration method derives the partial non-parametric pressure
. (1) Pressure underestimation: as previously explained, the integration method derives the partial non-parametric pressure  (over the finite measured energy range) that is always smaller than the total parametric pressure
(over the finite measured energy range) that is always smaller than the total parametric pressure  . (2) Irregularity & non-smoothness: physical structures such as the Ribbon appear discontinuous or/and noisy in the sky map of
. (2) Irregularity & non-smoothness: physical structures such as the Ribbon appear discontinuous or/and noisy in the sky map of  , while they are rather clearer and smoother in the map of
, while they are rather clearer and smoother in the map of  . (3) Dependence on other sky maps: as shown by Equation (8), the pressure
. (3) Dependence on other sky maps: as shown by Equation (8), the pressure  (Ω) depends on sky maps of other thermal or physical observables that cannot be derived from the integration method, e.g., emission region thickness in the inner heliosheath, Δr(Ω) (Figure 1(f)). However, these can be deduced through the parametric derivation of pressure,
(Ω) depends on sky maps of other thermal or physical observables that cannot be derived from the integration method, e.g., emission region thickness in the inner heliosheath, Δr(Ω) (Figure 1(f)). However, these can be deduced through the parametric derivation of pressure,  (Ω). (4) Availability of other thermal observables: no thermal observables other than the non-parametric pressure are derived from the integration method. In contrast, in order to derive the parametric pressure, we first derive other thermal observables and their sky maps, e.g., κ(Ω),
(Ω). (4) Availability of other thermal observables: no thermal observables other than the non-parametric pressure are derived from the integration method. In contrast, in order to derive the parametric pressure, we first derive other thermal observables and their sky maps, e.g., κ(Ω),  ,
,  , which are crucial for characterizing the thermodynamic processes.
, which are crucial for characterizing the thermodynamic processes.
3.3. Parametric and Non-parametric Partial Pressures in IBEX-Hi
It is interesting to compare the directly extracted partial non-parametric pressure,  (Equation (10)) with that obtained by partially integrating the parametric distribution over the IBEX-Hi energy range,
(Equation (10)) with that obtained by partially integrating the parametric distribution over the IBEX-Hi energy range,  (Appendix C),
(Appendix C),
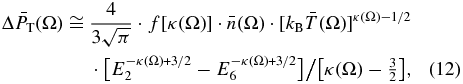
and
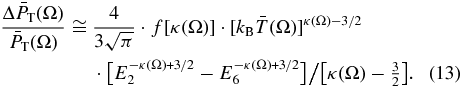
As shown in Figure 3, the sky maps of  and
and  are nearly identical.
are nearly identical.
Figure 3. Sky maps of (a) the partial non-parametric pressure  and (b) the partial parametric pressure
and (b) the partial parametric pressure  , both calculated over the IBEX-Hi energy range. The two sky maps are virtually identical. This verifies the validity of the technique of parametric pressure estimation used by Livadiotis et al. (2011), and that the proton plasma in the inner heliosheath is well described by the kappa distribution over the IBEX-Hi energy range.
, both calculated over the IBEX-Hi energy range. The two sky maps are virtually identical. This verifies the validity of the technique of parametric pressure estimation used by Livadiotis et al. (2011), and that the proton plasma in the inner heliosheath is well described by the kappa distribution over the IBEX-Hi energy range.
Download figure:
Standard image High-resolution image3.4. Comparing the Two Partial Pressures
While the two sky maps of partial pressures  and
and  appear to be almost identical, we examine the small differences between these two sky maps in Figure 4. In panels (a) and (b) we show the ratio
appear to be almost identical, we examine the small differences between these two sky maps in Figure 4. In panels (a) and (b) we show the ratio  /
/ and difference
and difference  −
− , while panel (c) provides their difference normalized to the total pressure, (
, while panel (c) provides their difference normalized to the total pressure, ( −
− )/
)/ .
.
Figure 4. Sky maps of (a)  /
/ , (b)
, (b)  −
− , and (c) (
, and (c) ( −
− )/
)/ show subtle, systematic differences. The respective histograms are shown in panels (d)–(f). Note that the most frequent value of the pressure variation
show subtle, systematic differences. The respective histograms are shown in panels (d)–(f). Note that the most frequent value of the pressure variation  −
− is ∼0.015 pdyn cm−2, that is (
is ∼0.015 pdyn cm−2, that is ( −
− )/
)/ ∼ 0.015 pdyn cm−2/0.6 pdyn cm−2 ∼ 2.5% of the pressure values
∼ 0.015 pdyn cm−2/0.6 pdyn cm−2 ∼ 2.5% of the pressure values  (or
(or  ) shown in Figure 2(e). The estimated relative error of pressure values,
) shown in Figure 2(e). The estimated relative error of pressure values,  , that is consistent with the relative error of the detected ENA flux ∼5%, covers the pressure difference of ∼2.5%. Therefore, the sky maps of the partial pressures
, that is consistent with the relative error of the detected ENA flux ∼5%, covers the pressure difference of ∼2.5%. Therefore, the sky maps of the partial pressures  and
and  are virtually identical, as also shown in Figure 3.
are virtually identical, as also shown in Figure 3.
Download figure:
Standard image High-resolution imageAs we will see in Section 6.1, some slight variations between the sky maps of the two partial pressures  and
and  can be related to newly formed PUIs and/or the bimodal structure of solar wind on the ENA flux spectra. However, the variation of the two pressure covers only a small portion of the partial pressure (∼2.5%). It is straightforward then to ask why the PUI partial pressure cannot be detected in the IBEX-Hi energy region; this will be examined in Section 5.2. Next, we verify that the kappa distribution well describes the proton population in the inner heliosheath.
can be related to newly formed PUIs and/or the bimodal structure of solar wind on the ENA flux spectra. However, the variation of the two pressure covers only a small portion of the partial pressure (∼2.5%). It is straightforward then to ask why the PUI partial pressure cannot be detected in the IBEX-Hi energy region; this will be examined in Section 5.2. Next, we verify that the kappa distribution well describes the proton population in the inner heliosheath.
Any proton distribution that can be reduced to a power-law spectrum gives near identical sky maps of parametric and non-parametric partial pressures. Indeed, Equation (B14) gives the partial non-parametric pressure by integrating the ENA flux,
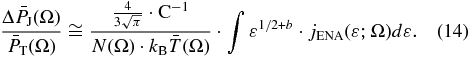
Then, substituting the ENA flux power-law given in Equation (2), and integrating in the IBEX-Hi interval, we derive
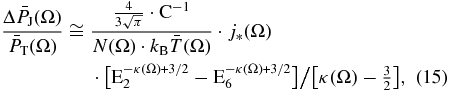
and, substituting the 1 keV flux j* from Equation (3), we find
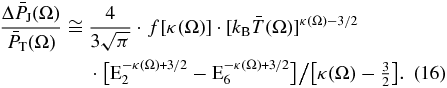
This equals the parametric pressure ratio, as given in Equation (13), i.e.,
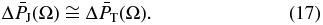
Therefore, the fact that the two partial pressure sky maps are almost identical verifies that the proton distribution in the inner heliosheath is a power-law, or any other function that can be reduced into a power-law in the examined IBEX-Hi energy range. The kappa distribution can lead to a power-law ENA spectra under the four conditions given in Section 2.
4. DISTRIBUTION OF PRESSURE IN ENERGY-FLUX SPECTRA
Having the partial pressure in the IBEX-Hi energy range covering only a small fraction of the total pressure (with most frequent values ∼0.6 pdyn cm−2 and ∼2.1 pdyn cm−2, respectively, that is with ratio ∼29%), then we must account for the unobserved ∼1.7 pdyn cm−2, which must lie at energies outside the energy range of IBEX-Hi. In order to understand the energy distribution of partial pressure, we first derive analytically the specific energy for which the ENA flux has a maximum. This maximum flux energy obviously resides below the lowest energy of the IBEX-Hi range, in which the flux asymptotically approaches the power-law spectrum of Equation (2).
In general, jENA(ε) can be approximated by
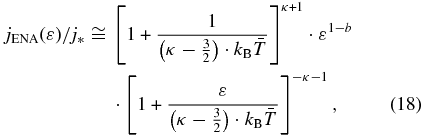
(see Equation (D3)) with the 1 keV flux, j*, given by
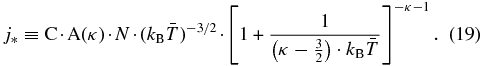
At high energies, Equation (18) is reduced to the power-law spectrum Equation (2), a characteristic of the IBEX-Hi energy range. The maximum value of Equation (18) is obtained at a much lower energy (see Equation (D9))
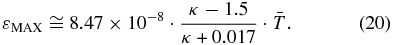
In all the above equations, the underlying proton distribution function is modeled by the kappa distribution.
The ENA flux does not directly correspond to the energy profile of the partial pressure. The latter is better described by the differential pressure JP, normalized over the total pressure and averaged over the inner heliosheath thickness. This is defined by

In Appendix D, we show that JP has the following energy function (Equation (D15)),
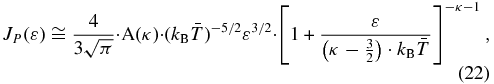
with a maximum at energy (Equation (D16)),
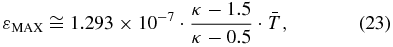
with the energy ε given in keV and T in K.
Figure 5 plots the sky maps and the histograms of the values of the maximum energy εMAX in eV for both the functions of the ENA flux, jENA(ε)/j* (Equation (18)), and the differential pressure, JP(ε) (Equation (22)). We observe that the most frequent values are ∼30 eV for the ENA flux and ∼60 eV for the differential pressure.
Figure 5. Sky maps of the maximum energy values εMAX of the functions of (a) ENA flux, jENA(ε)/j* (Equation (18)), and (b) the differential pressure, JP(ε). Panels (c) and (d) show the relevant histograms. (Each histogram shows the energy ε on a logarithmic scale (above), and log ε on linear scale (below).) The most frequent maximum energy εMAX of the ENA flux is ∼30 eV, while for the differential pressure is about twice as large, ∼60 eV.
Download figure:
Standard image High-resolution imageFurthermore, we will derive the partial pressure for energy regions other than IBEX-Hi. For this reason, we illustrate the ENA flux jENA(ε) and the differential partial pressure, JP(ε), for some values of κ and  . We choose the most frequent values in the inner heliosphere (Livadiotis et al. 2011; Livadiotis & McComas 2012a) that is κ ≈ 1.7,
. We choose the most frequent values in the inner heliosphere (Livadiotis et al. 2011; Livadiotis & McComas 2012a) that is κ ≈ 1.7,  . Then, Equations (18) and (22) give
. Then, Equations (18) and (22) give
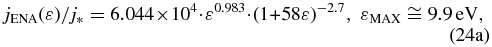
and
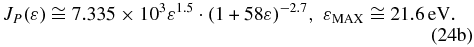
Figure 6 plots these energy functions of jENA(ε)/j* and JP(ε) in the same diagram. We observe that the partial pressures as a percentage of the total pressure in the energy ranges of IBEX-Lo and IBEX-Hi are ∼35% and ∼28%, respectively. A small portion ∼6% of the total pressure lies within the energy interval 0 ⩽ ε ⩽ 30 eV that is below the IBEX-Lo energy range, while a ∼31% of the total pressure, similar to that within the IBEX-Lo and IBEX-Hi energy ranges, lies above the IBEX-Hi energy range, i.e., 6 keV ⩽ ε < ∞ IBEX-Hi. The partial pressure is similar for the IBEX-Lo and IBEX-Hi energy ranges, in agreement with the results of Fuselier et al. (2012). Additional support of the apportionment of partial pressures over these energy ranges comes from the ratio of the most frequent value of the partial pressure in the IBEX-Hi energy range ∼0.6 pdyn cm−2, over the most frequent value of the total pressure ∼2.1 pdyn cm−2, that is ∼28.6%, i.e., very close to the ∼28% estimated above.
Figure 6. ENA flux jENA(ε)/j* (blue dash-dotted curve), and the differential pressure JP(ε) (orange solid curve), modeled by Equations (24a) and (24b), are plotted as functions of energy on log–log scale. ΔP(%) (red) counts the normalized partial pressure ∫JP(ε)dε, in each of the four energy intervals: 0 ⩽ ε ⩽ 30 eV (yellow), IBEX-Lo: 30 eV ⩽ ε ⩽ 0.5 keV (green), IBEX-Hi: 0.5 keV ⩽ ε ⩽ 6 keV (light blue), and 6 keV ⩽ ε < ∞ (magenta).
Download figure:
Standard image High-resolution imageThe distribution of partial pressure in the above four energy intervals can be derived separately for each pixel, and a sky map at each energy interval can be constructed. In particular, for each pixel we integrate Equation (22) over the desired energy integral, and substitute the corresponding values of κ(Ω) and T(Ω) (Livadiotis et al. 2011). Hence, we derive the partial pressure for each pixel, and for each of the above four energy intervals. The sky maps and histograms of these partial pressures are shown in Figures 7(a)–(d) and Figures 7(e)–(h), respectively.
Figure 7. (a)–(d) Sky maps of the partial pressures for the four energy intervals 0 ⩽ ε ⩽ 30 eV (yellow), 30 eV ⩽ ε ⩽ 0.5 keV (green), 0.5 keV ⩽ ε ⩽ 6 keV (light blue), and 6 keV ⩽ ε < ∞ (magenta), respectively. (e)–(h) Histograms of the partial pressures for the respective energy intervals.
Download figure:
Standard image High-resolution imageWe note that the Ribbon appears clearly only in the partial pressure sky maps of IBEX-Lo and IBEX-Hi. However, the Ribbon flux spectra may flatten at energies below IBEX-Lo, forming a knee at about 1 keV (Fuselier et al. 2012). This behavior of Ribbon cannot be assessed by Equation (18), and possibly affects its appearance in the IBEX-Lo energy region. Extrapolating the function of differential pressure below (or above) the IBEX-Hi energy range is interwoven with the assumption that the source proton distribution is still described by the same distribution (kappa distribution). Any sudden changes of the source protons and the ENA spectra, strictly localized at energies out of the IBEX-Hi range, cannot be described by the modeled extrapolation.
The values of the partial pressures in the IBEX-Lo and IBEX-Hi are quite similar (in agreement with the results of Fuselier et al. 2012). For the energy intervals lower than IBEX-Lo and higher than IBEX-Hi, the Ribbon is largely indistinct. For the energy interval lower than IBEX-Lo, the partial pressure near the equator is small ∼0.07 pdyn cm−2, while near the poles is larger ∼0.5 pdyn cm−2. Moreover, the ''knot'' and high-latitude extension of the Ribbon is still present for the energy interval higher than IBEX-Hi, likely owing to its higher solar speed solar wind source (McComas et al. 2009c, 2010). Finally, we note that the sky map of partial pressure for the IBEX-Hi (Figure 7(c)) is very close to the one shown in Figure 3(b) that plots partial pressure under Equation (12). Integrating Equation (22) over IBEX-Hi gives the partial pressure plotted in Figure 7(c). At the high-energy approximation, ε ≫ (κ − 3/2)kBT, this pressure is given by Equation (13) that is plotted in Figure 3(b). The slight differences between these two maps is due to that high energy approximation.
5. DISCUSSION
5.1. The Effect of PUI Distribution on the ENA Flux Spectra
Slight variations between the sky maps of the two partial pressures  and
and  may be due to a non-kappa-distributed source of proton populations; the spherical shell distribution of newly formed PUIs can cause such variations. Indeed, significant PUI densities in the source region of ENA emission should impact the detected ENA flux and in particular its spectral shape, and thus, the derived non-parametric pressure
may be due to a non-kappa-distributed source of proton populations; the spherical shell distribution of newly formed PUIs can cause such variations. Indeed, significant PUI densities in the source region of ENA emission should impact the detected ENA flux and in particular its spectral shape, and thus, the derived non-parametric pressure  .
.
One way to connect the PUI distributions with IBEX spectra is through the spectral curvature. It was shown by Livadiotis et al. (2012) that PUIs bend the ENA energy-flux IBEX-Hi spectra, from linear to concave upward (on log–log scale), increasing thus, their spectral curvature. This curvature is a valuable and sensitive tool to evaluate the presence of PUIs in the emission region and their influence as an independent source population. For example, a possible correlation between the spectral curvature and the partial pressure variation could verify the presence of PUIs in the partial pressure  .
.
The pressure variation  −
− , and the effect of PUI distribution on ENA spectra are compared in Figure 8, which co-plots the sky maps of partial pressure normalized variation [
, and the effect of PUI distribution on ENA spectra are compared in Figure 8, which co-plots the sky maps of partial pressure normalized variation [ (Ω) −
(Ω) − (Ω)]/
(Ω)]/ (Ω) and the spectral curvature coefficient α (Appendix A in Livadiotis et al. 2012). Note that the pressure variation could be positive (red) or negative (blue), depending on the cutoff energy of the PUI distribution (Appendix B in Livadiotis et al. 2012). The large values of positive and negative pressure variation coincide with the two (ecliptic) meridional "columns" of high positive curvature, located for longitudes |φ−50| < 400 and |φ−1500| < 350.
(Ω) and the spectral curvature coefficient α (Appendix A in Livadiotis et al. 2012). Note that the pressure variation could be positive (red) or negative (blue), depending on the cutoff energy of the PUI distribution (Appendix B in Livadiotis et al. 2012). The large values of positive and negative pressure variation coincide with the two (ecliptic) meridional "columns" of high positive curvature, located for longitudes |φ−50| < 400 and |φ−1500| < 350.
Figure 8. Sky maps of (a) ( −
− )/
)/ , and (b) spectral curvature coefficient α (Livadiotis et al. 2012). (In panel (a), pixels in black have spectral shapes that cannot be described by a kappa distribution.)
, and (b) spectral curvature coefficient α (Livadiotis et al. 2012). (In panel (a), pixels in black have spectral shapes that cannot be described by a kappa distribution.)
Download figure:
Standard image High-resolution imageThe variation between the two partial pressures might possibly be due to the presence of newly formed PUIs that still act as an independent population in the source region. This variation is small, thus the same may hold for the partial pressure of PUIs. Indeed, the partial pressure of newly formed PUIs in the IBEX-Hi could not exceed ∼0.1 pdyn cm−2, while on average is ∼0.015 pdyn cm−2 (Figure 4(e)). The average partial pressure  (or
(or  ) is ∼0.6 pdyn cm−2 (Figure 2(e)), hence, the pressure variation is ∼2.5%. However, the estimated relative error of pressure values,
) is ∼0.6 pdyn cm−2 (Figure 2(e)), hence, the pressure variation is ∼2.5%. However, the estimated relative error of pressure values,  , that is consistent with the relative error of the detected ENA flux ∼5%, covers the pressure difference of ∼2.5%. It is therefore expected that the partial pressure of PUIs in the IBEX-Hi energy range would be no more than ∼2.5% of
, that is consistent with the relative error of the detected ENA flux ∼5%, covers the pressure difference of ∼2.5%. It is therefore expected that the partial pressure of PUIs in the IBEX-Hi energy range would be no more than ∼2.5% of  , or at least, would be determined by the range of pressure uncertainties. Surely, a similar analysis for the three years of IBEX data will dramatically increase the statistics as shown in McComas et al. (2012).
, or at least, would be determined by the range of pressure uncertainties. Surely, a similar analysis for the three years of IBEX data will dramatically increase the statistics as shown in McComas et al. (2012).
The partial pressure of newly formed PUIs in the IBEX-Hi energy range is certainly small, but it qualifies only those sky-map pixels (86.5% of the sky, Figure 9(b)), for which the IBEX-Hi spectra are sufficiently linear (on log–log scale) so the multiple linear regression can apply. Pixels that cannot be described by a kappa distribution are depicted in black in the sky maps, and most of these pixels lie at high latitudes near the poles. This may be due to the presence of more than one proton population, so the emission region would not be characterized by a single-dominant kappa distribution. For example, an excess of PUIs or the coexistence of the fast/slow solar wind modes (Livadiotis et al. 2012). Even a single but anisotropic kappa distribution could break the linearity of spectra enough so that the multiple linear regression could not be applied. The parametric analysis of Livadiotis et al. (2011) cannot derive and qualify the pressure of solar wind or pick-up protons for the near-polar pixels, for which the spectra clearly deviate from a single power-law (and Equation (2)).
Figure 9. (a) Fraction X(ϑ) of sky map pixels as a function of sky map latitude ϑ, whose underlying proton distribution in the emission region can be represented by a kappa distribution. (b) Percentages of the celestial sphere covered by the Ribbon (red), the globally distributed ENAs (green), and the complementary area that is non-describable by kappa distributions (black).
Download figure:
Standard image High-resolution imageFigure 9(a) plots the normalized fraction X(ϑ) of the number of pixels (%) at each latitude ϑ of the sky map (latitudinal step is 60), whose ENA spectra are sufficiently linear, and thus, the underlying proton distribution in the source region can be described as a kappa distribution. At low latitudes, we observe a broad region centered near the equator with almost no black pixels, i.e., X≅100% for −360 ⩽ ϑ ⩽ 360. At higher latitudes, the fraction X decreases linearly with |∂X/∂ϑ|≅2. This trend spans ∼4 latitudinal pixels (∼240) in the south and ∼6 latitudinal pixels (∼360) in the north hemispheres. In the polar regions, X becomes quasi-constant with X≅50% at south and X≅40% at north. As a whole, the black pixels (non-kappa) cover 13.5% of the sky, while the rest of 86.5% is divided in 26.1% that is the sky fraction covered by the Ribbon and 60.4% covered by the globally distributed flux, as shown in Figure 9(b).
These results reveal a strong heliospheric latitudinal symmetry of X(ϑ) that closely follows the global structure of the solar wind: slow wind at low latitudes, fast wind at high latitudes, and a mixture of fast and slow at intermediate latitudes (McComas et al. 2003). However, solar wind flow bends within the inner heliosheath, thus along the LoS at high latitudes, ENAs are generated from source protons of both the slow and fast solar wind modes (Dayeh et al. 2012). Hence, at high latitudes, a smaller part of the sky can be described by a single kappa distribution; this may be caused by either the presence of newly formed PUIs and their influence on the proton distribution in the heliosheath, and/or the bimodal structure of solar wind (Livadiotis et al. 2012).
This analysis, however, is not decisive about the pressure either of solar wind or pick-up protons at these polar regions. The analysis of low-latitude spectra has shown that newly formed PUIs do not efficiently contribute to the partial pressure in the IBEX-Hi range and can be connected only to ∼2.5% of the average partial pressure. Several questions rise regarding this lack of PUI pressure in the IBEX-Hi, which we examine next.
5.2. Where is the PUI Contribution in the Pressure of the Inner Heliosheath?
Why is a significant partial pressure not directly attributable to PUIs detected in the IBEX-Hi energy range? Furthermore, what is the primary energy range in which the effects of PUIs should be observed? The matching of the two partial pressures  and
and  in the IBEX-Hi energy range has shown that the PUIs do not efficiently contribute to the partial pressure of this energy range (∼2.5% of the average total pressure). The same conclusion holds for the IBEX-Lo energy range. The distribution of differential pressure reveals that the partial pressure
in the IBEX-Hi energy range has shown that the PUIs do not efficiently contribute to the partial pressure of this energy range (∼2.5% of the average total pressure). The same conclusion holds for the IBEX-Lo energy range. The distribution of differential pressure reveals that the partial pressure  in the IBEX-Lo energy range is similar to
in the IBEX-Lo energy range is similar to  , as estimated by Fuselier et al. (2012) using the integration method. Here, for energies lower than the IBEX-Lo, we find only a small (∼6%) contribution to the total pressure. Furthermore, Livadiotis et al. (2012) have shown that PUIs, if present as an independent population in the heliosheath, should be detected by the first IBEX-Hi energy passbands.
, as estimated by Fuselier et al. (2012) using the integration method. Here, for energies lower than the IBEX-Lo, we find only a small (∼6%) contribution to the total pressure. Furthermore, Livadiotis et al. (2012) have shown that PUIs, if present as an independent population in the heliosheath, should be detected by the first IBEX-Hi energy passbands.
An explanation for this enigma was proposed by Livadiotis & McComas (2011a) in which PUIs do not exist as a unique and independent population. In particular, the two populations of solar wind and pick-up protons are merged into a single proton population that resides in a single stationary state and described by a single kappa distribution.
Above some source surface in the corona, the solar wind is generally conceptualized as a stream of electrons and ions flowing radially outward with constant velocities. As the solar wind continues for flow outward, particularly beyond a few AU, it is continuously enriched with interstellar PUIs. After some time, the pick-up ions are incorporated with the original solar wind, forming a single, undistinguished distribution that is a kappa distribution with a new kappa index. We refer to this as "incorporated solar wind" in order to distinguish it from the "original solar wind" coming directly from the Sun and without the PUI contribution.
PUIs are generated, entrained in, and merged with the solar wind distribution throughout the solar wind flow in the heliosphere. These ''matured'' PUIs, carried on from the space upstream the termination shock, are transformed through the termination shock (Zank et al. 2010), accompanying the original solar wind protons in the inner heliosheath. We distinguish this transformed (tr) PUI population from the newly formed (nf) PUIs that are generated in the inner heliosheath and continue to act as a population that is independent from the incorporated solar wind.
The transition of space plasmas in near-equilibrium stationary states is characterized by some monotonic entropic behavior (Livadiotis & McComas 2010a). As the entropy decreases, the κ-index also decreases, and the system is diverted further from equilibrium. The addition and incorporation of highly ordered PUI distributions can increase the ordering of space plasmas, decreasing their entropy, and thus, decreasing their kappa index (that is driving them away from thermal equilibrium).
Figure 10(a) illustrates solar wind protons, p+(S), residing in a stationary state with kappa index κ1 and entropy S1, that are mixed with pick-up protons, p+(PUI), forming the hybrid state of undistinguishable protons, [p+(S)  p+(PUI)]*. Ultimately, the hybrid state degenerates into a new stationary state with kappa index κ2 and entropy S2. In Figure 10(b), we depict the ENA flux spectra that follows from the kappa distributed original solar wind protons, p+(SW), and from both the solar wind and pick-up protons, p+(SW)+p+(PUI). In the absence of PUIs, the spectrum is linear (on log–log scale) for high energies, with spectral index γ close to the kappa value (∼κ1). In the presence of PUI distributions, the spectral curvature increases and the spectra cannot be described by a power-law; beyond an upper limit (here ∼2 keV), the influence of PUI distribution is neglected. Livadiotis et al. (2012) showed that in the most of the cases, this PUI cut-off appears after the first or the second IBEX-Hi energy passbands, while it is always included in the IBEX-Hi energy range. It is therefore unexpected that we cannot see a large deviation between the two partial pressures in the IBEX-Hi. This would be the case if the two proton populations, p+(SW)+p+(PUI), have been incorporated in a single kappa distributed proton population, p+(iSW). This case is shown in Figure 10(c), where the ENA spectrum is constructed by the incorporated solar wind protons, p+(iSW), which are kappa distributed with a kappa index ∼κ2 smaller than that of the original solar wind protons, κ1 (κ1 = 2 > κ2 = 1.6 > 1.5). The presence of some newly formed (nf) PUIs is less effective in reducing the linearity of the spectrum, and thus, the multiple linear regression technique can successfully apply.
p+(PUI)]*. Ultimately, the hybrid state degenerates into a new stationary state with kappa index κ2 and entropy S2. In Figure 10(b), we depict the ENA flux spectra that follows from the kappa distributed original solar wind protons, p+(SW), and from both the solar wind and pick-up protons, p+(SW)+p+(PUI). In the absence of PUIs, the spectrum is linear (on log–log scale) for high energies, with spectral index γ close to the kappa value (∼κ1). In the presence of PUI distributions, the spectral curvature increases and the spectra cannot be described by a power-law; beyond an upper limit (here ∼2 keV), the influence of PUI distribution is neglected. Livadiotis et al. (2012) showed that in the most of the cases, this PUI cut-off appears after the first or the second IBEX-Hi energy passbands, while it is always included in the IBEX-Hi energy range. It is therefore unexpected that we cannot see a large deviation between the two partial pressures in the IBEX-Hi. This would be the case if the two proton populations, p+(SW)+p+(PUI), have been incorporated in a single kappa distributed proton population, p+(iSW). This case is shown in Figure 10(c), where the ENA spectrum is constructed by the incorporated solar wind protons, p+(iSW), which are kappa distributed with a kappa index ∼κ2 smaller than that of the original solar wind protons, κ1 (κ1 = 2 > κ2 = 1.6 > 1.5). The presence of some newly formed (nf) PUIs is less effective in reducing the linearity of the spectrum, and thus, the multiple linear regression technique can successfully apply.
Figure 10. (a) In a diagram of entropy S vs. kappa index κ, we map solar wind protons, p+(SW), residing in a stationary state with kappa index κ1 and entropy S1. These are mixed with pick-up protons, p+(PUI), forming a hybrid state of undistinguished protons, [p+(SW)  p+(PUI)]*. The hybrid state degenerates into a new stationary state of incorporated solar wind protons, p+(iSW), with kappa index κ2 and entropy S2, where κ1 > κ2 and S1 > S2. The incorporation of highly ordered PUI distributions increases the ordering of space plasmas, decreasing their average entropy and the kappa indices. (b) The ENA flux spectra that corresponds to solar wind protons (blue), described by kappa distribution of kappa index κ1, and to their mixture with PUIs (red). (c) The ENA flux spectra that correspond to the incorporated solar wind protons (blue), described by kappa distribution of kappa index κ2, and to their mixture with newly formed PUIs (red). (χ is the PUI density over total proton density; IBEX-Hi energy passbands are somewhat broad but are nominally located at E2 = 0.71 keV (light blue), E3 = 1.11 keV (green), E4 = 1.74 keV (magenta), E5 = 2.73 keV (brown), and E6 = 4.29 keV (gray).)
p+(PUI)]*. The hybrid state degenerates into a new stationary state of incorporated solar wind protons, p+(iSW), with kappa index κ2 and entropy S2, where κ1 > κ2 and S1 > S2. The incorporation of highly ordered PUI distributions increases the ordering of space plasmas, decreasing their average entropy and the kappa indices. (b) The ENA flux spectra that corresponds to solar wind protons (blue), described by kappa distribution of kappa index κ1, and to their mixture with PUIs (red). (c) The ENA flux spectra that correspond to the incorporated solar wind protons (blue), described by kappa distribution of kappa index κ2, and to their mixture with newly formed PUIs (red). (χ is the PUI density over total proton density; IBEX-Hi energy passbands are somewhat broad but are nominally located at E2 = 0.71 keV (light blue), E3 = 1.11 keV (green), E4 = 1.74 keV (magenta), E5 = 2.73 keV (brown), and E6 = 4.29 keV (gray).)
Download figure:
Standard image High-resolution imageThe results of simulations by Wu et al. (2010) suggest that an incorporated solar wind proton distribution exists in the inner heliosheath and may be well characterized by a kappa distribution. Similar results were obtained for four different PUI distributions upstream the termination shock. The kappa distribution can be considered as an approximate mixture of a Maxwellian and a suprathermal distribution (Livadiotis & McComas 2009). The Maxwellian distribution can approximately describe the solar wind protons across the shock, while the heated pick-up protons contribute to the suprathermal distribution. Heerikhuisen et al. (2008) considered this interpretation of the downstream kappa distribution for simulations in the inner heliosheath.
5.3. Partial and Total Pressure of the Globally Distributed Flux
Here we construct the sky maps of the partial and total parametric pressure for the globally distributed ENA flux data sets. These have been methodologically separated from the Ribbon by Schwadron et al. (2011). In Figure 11, we observe that the highest partial pressure resides in the IBEX-Lo and IBEX-Hi energy ranges. In addition, the most frequent total pressure is still  ∼ 2.1 pdyn cm−2, which is the same most frequent value of the pressure taken from the primary sky maps that include Ribbon (Figure 2). This also coincides with the pressure value ∼1.9 pdyn cm−2 calculated by Schwadron et al. (2011).
∼ 2.1 pdyn cm−2, which is the same most frequent value of the pressure taken from the primary sky maps that include Ribbon (Figure 2). This also coincides with the pressure value ∼1.9 pdyn cm−2 calculated by Schwadron et al. (2011).
Figure 11. Sky maps and histograms of the parametric pressure including only the globally distributed flux data deduced by Schwadron et al. (2011). (a)–(d) Sky maps of the partial pressures for the four energy intervals 0 ⩽ ε ⩽ 30 eV (yellow), 30 eV ⩽ ε ⩽ 0.5 keV (green), 0.5 keV ⩽ ε ⩽ 6 keV (light blue), and 6 keV ⩽ ε < ∞ (magenta), respectively. (f)–(i) Histograms of the partial pressures for the respective energy intervals. Panels (e) and (j) show the sky map and histogram of the total pressure, 0 ⩽ ε < ∞, respectively.
Download figure:
Standard image High-resolution imageThe pressure of the globally distributed flux is interpreted as the thermal pressure of the proton plasma in the inner heliosheath. However, it is not easy to interpret the pressure that corresponds to the Ribbon emissions. Heerikhuisen et al. (2010) and Chalov et al. (2010) used global MHD models to quantitatively reproduce a Ribbon by assuming the secondary ENA source (McComas et al. 2009b; 2010, 2012). According to this, protons from the inner heliosheath become neutralized, travel outward past the heliopause into the outer heliosheath, become ionized and picked up on the draped interstellar magnetic field in the outer heliosheath, and after some time, some become re-neutralized and emitted as ENAs back in toward the inner heliosphere. If correct, this mechanism might be useful for interpreting the Ribbon fluxes in terms of their pressure. The estimated Ribbon pressure remains after subtraction of the globally distributed flux pressure (Figures 11(e) and (j)) from the total pressure (Figures 2(a) and (d)). This may be indirectly related to the inner heliosheath pressure.
6. CONCLUSIONS
Here we summarize the main conclusions of this study.
- 1.The parametric and non-parametric partial pressures yield nearly identical sky maps over the IBEX-Hi energy range.The partial pressure over the IBEX-Hi was calculated using two different methods. The non-parametric partial pressure was derived by integrating the observed ENA flux over the IBEX-Hi energy range. The parametric partial pressure was analytically derived by integrating the specific thermodynamic function used for describing the proton plasma population in the inner heliosheath. The sky maps of the parametric and non-parametric partial pressures were found to be almost identical, with strong agreement between the two different methodologies. Moreover, the proton plasma in the inner heliosheath, which is the underlying population for ENA emission, is well described by a kappa distribution. Any distribution function that degenerates into a power-law in the IBEX-Hi energy range, and thus, give a power-law ENA spectra, can also lead to similar partial pressure sky maps. The kappa distribution is such a function, having an asymptotic power-law behavior in the IBEX-Hi range.
- 2.Newly formed PUIs in the inner heliosphere may contribute to the small difference observed between the parametric and non-parametric partial pressure maps.The slight differences between the two partial pressures can be related to the presence of protons that are not well described by a kappa distribution, especially in the high latitudes. These may be newly formed PUIs having spherical shell distributions (Livadiotis & McComas 2011a) or even filled spherical shell distributions (Vasyliunas & Siscoe 1976). In addition, they can be protons from both the slow and fast solar wind modes. These non-kappa distributed protons increase the curvature of ENA spectra (on log–log scale), causing deviation from the power-law asymptotic behavior of kappa distribution that leads to linear ENA spectra (Livadiotis et al. 2012).
- 3.Matured PUIs in the inner heliosheath are mostly kappa distributed.Newly formed PUIs are typically described by non-kappa distributions. Ultimately, though, matured PUIs incorporate with solar wind ions into one single ion population, statistically described by a common distribution function, the kappa distribution. In parallel, other newly formed, non-kappa-distributed PUIs, continuously accompanying the incorporated plasma.
- 4.The spectral distribution can be described by an analytical function of the ENA energy-flux spectra, and the maximum of this distribution occurs at ∼30 eV.Having confirmed that the source protons in the inner heliosheath are described by a kappa distribution, we retrieved the energy function of the ENA flux spectra. Then, we calculated the specific energy that maximizes the ENA flux, and constructed its sky map and histogram. The most frequent value is ∼30 eV.
- 5.Extrapolation of the partial pressure derived for the IBEX-Hi energy range is consistent with IBEX-Lo results and shows that the Ribbon can be clearly observed only in the IBEX-Lo and IBEX-Hi energy range.
- 6.We defined and described the differential pressure over the energy.This led to an estimation of the partial pressure over energy intervals other than the IBEX-Hi, such as the IBEX-Lo, or even for lower or higher energies. By extrapolating the kappa distribution that best fits the IBEX-Hi energy region, we found that the whole structure of Ribbon appears clearly primarily in the partial pressure sky maps of IBEX-Lo and IBEX-Hi, and not over lower or higher energies. Pressure maps for the Ribbon and globally distributed flux were quantified and compared; the globally distributed flux accurately reflects the inner heliosheath pressure. In particular, we calculated the partial pressure over certain energy ranges and the total pressure of the proton population in the inner heliosheath; we used (1) the original ENA flux data sets that include both the globally distributed flux and the Ribbon, and (2) the globally distributed ENA flux data alone, separated from the Ribbon emissions. We constructed the sky maps and histograms of the pressure values. The globally distributed flux leads directly to the inner heliosheath pressure; the Ribbon flux may be indirectly related to the same inner heliosheath pressure.
This work was carried out under the IBEX mission, which is part of NASA's Explorer program. George Livadiotis gratefully acknowledges useful discussions with Dr. Edmond Roelof related to the derivation of the non-parametric pressure by integrating the observed ENA flux.
APPENDIX A: VARIATION OF FITTING PARAMETERS
Consider the case of fitting a model to M data points leading to the optimal values of two modeling parameters, a, b. In order to examine the correlation between these parameters, we need more than one pair of values. The variation of fitting parameters' technique expands the pair of least-squares fit values (x, y) into a whole set of ν pairs: (x1, y1), ..., (xv, yv), as follows. First we remove one data point and derive the fit values from the remaining (M−1) data points. Thus, we have a number of M fit values for all the combinations of removing one data point. Similarly, we can have a number of M(M−1)/2 fit values for all the combinations of removing two data points, and generally, we can have a number of (Mm) ≡ M!/[m!(M − m)!] fit values for all the combinations of removing m data points. Therefore, the number of all the combinations of removing any number of data points less than or equal to m is  . Number ν is sufficiently large even when removing only a few data points, i.e., for M = 100 and m = 2 we have ν ≈ 5 × 103, and for m = 3 we have ν ≈ 1.7 × 105. The constructed ν pairs have values very close to the initial one (x, y) (for m ≪ M), i.e., within the 1σ interval x − δx ⩽ xi ⩽ x + δx, y − δy ⩽ yi ⩽ y + δy, ∀i = 1, ..., ν. It is important to note that through this technique we do not gain information about the fitting parameters but for the relation between these parameters. We apply this technique in the second fitting level. Normally, the first fitting level leads to a single pair values of kappa index κ and 1 keV flux j*. However, the second fitting needs some number of these pairs, so that to be applied in every pixel. This is possible through this technique that generates a number of pairs (κ, j*) (Livadiotis et al. 2011).
. Number ν is sufficiently large even when removing only a few data points, i.e., for M = 100 and m = 2 we have ν ≈ 5 × 103, and for m = 3 we have ν ≈ 1.7 × 105. The constructed ν pairs have values very close to the initial one (x, y) (for m ≪ M), i.e., within the 1σ interval x − δx ⩽ xi ⩽ x + δx, y − δy ⩽ yi ⩽ y + δy, ∀i = 1, ..., ν. It is important to note that through this technique we do not gain information about the fitting parameters but for the relation between these parameters. We apply this technique in the second fitting level. Normally, the first fitting level leads to a single pair values of kappa index κ and 1 keV flux j*. However, the second fitting needs some number of these pairs, so that to be applied in every pixel. This is possible through this technique that generates a number of pairs (κ, j*) (Livadiotis et al. 2011).
APPENDIX B: NON-PARAMETRIC PRESSURE
In this Appendix, we prove the non-parametric pressure relations given by Equations (8)–(11) of the main text. We begin from Equation (1) which gives ENA flux in terms of ion flux or ion phase space density,
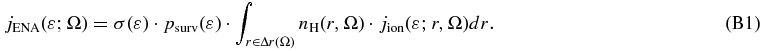
Note that the pressure is always defined in the plasma convective frame that is the frame of the bulk solar wind flow in the inner heliosheath; however, this is a negligible correction because the bulk flow in the inner heliosheath is quite smaller the thermal motion (Livadiotis et al. 2011, 2012). Furthermore, by substituting the ion flux jion(ε; r, Ω) = 1/2(m/2)−2 · n(r, Ω) · pion(ε; r, Ω) · ε, we obtain

where pion is the ion distribution of energy ε. If  is the distribution of the velocity vector
is the distribution of the velocity vector  , the distribution of its magnitude u is given by pion(u)gV(u)du, where gV(u)du = 4πu2du is the density of states. By means of the kinetic energy ε = (1/2)mu2, the distribution is given by pion(ε = (1/2)mu2) with gV(u)du = gE(ε)dε = 2π(m/2)−3/2ε1/2dε, so that ∫pion(u)gV(u)du = 1 = ∫pion(ε)gE(ε)dε = 1.
, the distribution of its magnitude u is given by pion(u)gV(u)du, where gV(u)du = 4πu2du is the density of states. By means of the kinetic energy ε = (1/2)mu2, the distribution is given by pion(ε = (1/2)mu2) with gV(u)du = gE(ε)dε = 2π(m/2)−3/2ε1/2dε, so that ∫pion(u)gV(u)du = 1 = ∫pion(ε)gE(ε)dε = 1.
Equation (B2) is written as
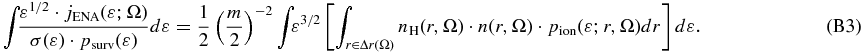
The right-hand side of Equation (B3) can be connected with pressure as follows:
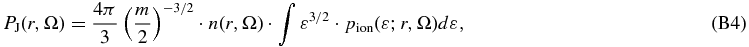
or
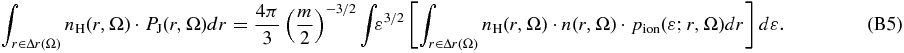
Note the factor that gives the radial mean of the phase-space distribution function fion = n · pion,
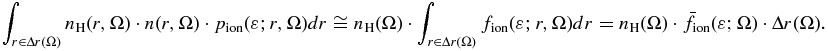
Both Equations (B3) and (B5) include this factor, so that it can be canceled out as follows:
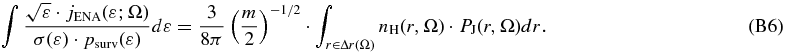
The right-hand side involves the radial mean pressure in the inner heliosheath,
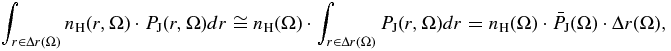
hence, we end up with Equation (B7) that is Equation (8) of the main text,
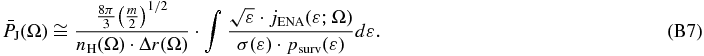
Furthermore, using the dimensions of the involved physical quantities, we write Equation (B7) as follows:
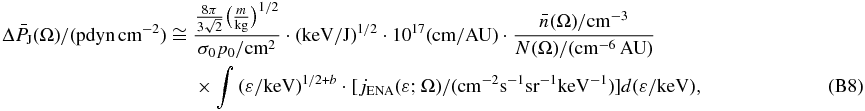
where cross section and survival probability were expressed in power-law for the IBEX-Hi energy range, i.e., σ(ε)psurv(ε) = σ0p0(ε/1 keV)−b with σ0p0≅(1.77 ± 0.15) × 10−15 cm2, b≅0.017 ± 0.016 (Livadiotis et al. 2011). Then,
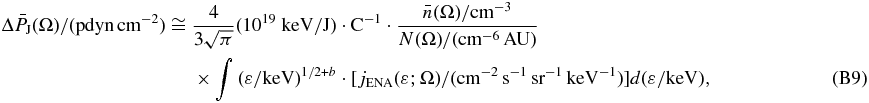
where we used the same constant as in the analysis of Livadiotis et al. (2011),
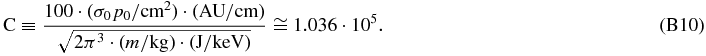
Equation (B8) can be expressed as a fraction to the total pressure,
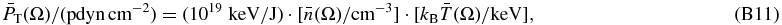
i.e.,
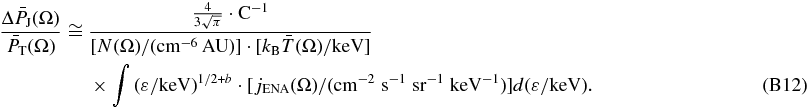
Finally, Equations (B9) and (B12) can be written without including any units,
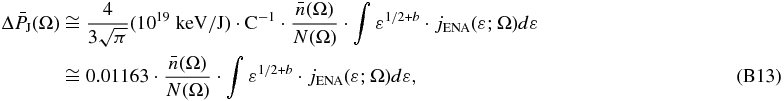
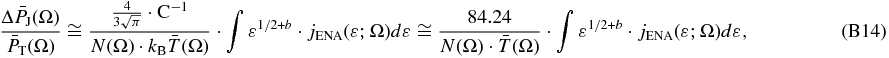
where the pressures are in pdyn cm-2, the density factor N in cm-6 AU, the density  in cm-3, the energies ε and
in cm-3, the energies ε and  in keV, the flux jENA in cm−2 s−1 sr−1 keV−1, and the temperature
in keV, the flux jENA in cm−2 s−1 sr−1 keV−1, and the temperature  in K.
in K.
APPENDIX C: PARAMETRIC PRESSURE
In this Appendix, we prove the parametric pressure relations given by Equations (12) and (13) of the main text. We begin from the parametric thermal pressure that is
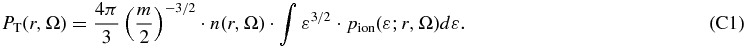
The ion distribution is given by the three-dimensional kappa distribution (Livadiotis & McComas 2009, 2011b)
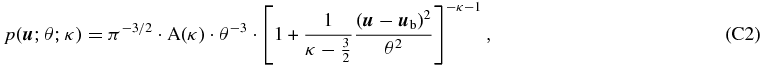
where  is the proton velocity in the bulk flow reference frame of the space plasma;
is the proton velocity in the bulk flow reference frame of the space plasma;  is the proton velocity, and
is the proton velocity, and  is the mean of
is the mean of  that represents the proton bulk flow velocity; both
that represents the proton bulk flow velocity; both  and
and  are in the heliospheric inertial frame; and
are in the heliospheric inertial frame; and  is a characteristic thermal speed-scale parameter that is simply the temperature in speed dimensions, where m and T are the proton mass and temperature, respectively; kB is Boltzmann's constant. The function A(κ) is given by A(κ) ≡ (κ − 3/2)−3/2 · Γ(κ + 1)/Γ(κ − 1/2). At thermal equilibrium, this approaches the limit A(κ → ∞) = 1 and Equation (C2) becomes a Maxwellian distribution.
is a characteristic thermal speed-scale parameter that is simply the temperature in speed dimensions, where m and T are the proton mass and temperature, respectively; kB is Boltzmann's constant. The function A(κ) is given by A(κ) ≡ (κ − 3/2)−3/2 · Γ(κ + 1)/Γ(κ − 1/2). At thermal equilibrium, this approaches the limit A(κ → ∞) = 1 and Equation (C2) becomes a Maxwellian distribution.
The kappa distribution is written in terms of proton energy ε in the inertial frame of the heliosphere
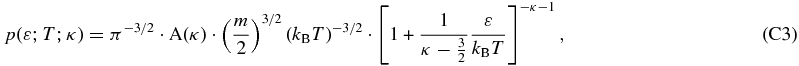
where  , namely, the bulk flow velocity
, namely, the bulk flow velocity  is quite smaller than its thermal motion and can be ignored. In addition, the IBEX spacecraft velocity
is quite smaller than its thermal motion and can be ignored. In addition, the IBEX spacecraft velocity  can also be ignored,
can also be ignored,  . Thus, ε stands also for the proton energy in the spacecraft frame.
. Thus, ε stands also for the proton energy in the spacecraft frame.
The total pressure corresponds to the integration of the kappa distribution in Equation (C1), over all the energies,
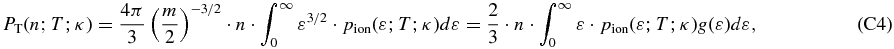
where g(ε) = 2π(m/2)−3/2ε1/2 is the three-dimensional density of energy states. Hence, we find the classical ideal gas state equation that holds for any non-equilibrium stationary state (any κ; Livadiotis & McComas 2012a),
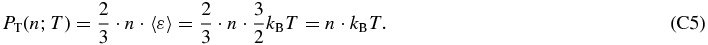
The partial pressure corresponds to the integration of the kappa distribution over the IBEX-Hi energy range. This resides in the high-energy region with asymptotic behavior ε ≫ (κ − 3/2)kBT, where the kappa distribution Equation (C3) is reduced to a power-law,
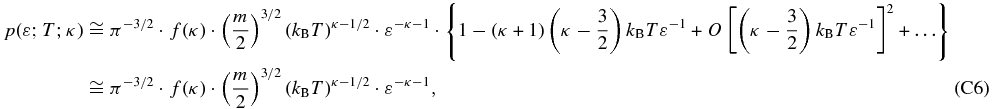
with
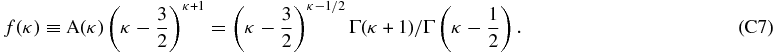
Hence, using Equation (C1), and integrating over the IBEX-Hi energy passbands (channels 2–6) that span E2 = 0.71 keV−E6 = 4.29 keV (Funsten et al. 2009b), we derive the partial parametric pressure
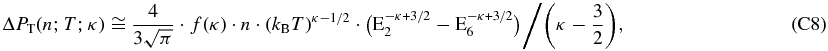
or

Given the radial mean over the inner heliosheath, we have
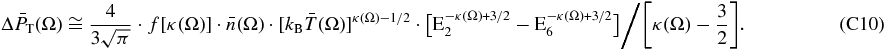
while for the total pressure in Equation (C5) gives

with their ratio given by
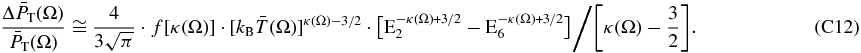
The energies E2 and E6 and thermal  are given in the same units, e.g., keV. (The partial pressure relations in Equations (C10) and (C12) are Equations (12) and (13) in the main text, respectively; the total pressure relation Equation (C11) is Equation (7) in the main text.)
are given in the same units, e.g., keV. (The partial pressure relations in Equations (C10) and (C12) are Equations (12) and (13) in the main text, respectively; the total pressure relation Equation (C11) is Equation (7) in the main text.)
APPENDIX D: ENERGY DEPENDENCE OF ENA FLUX AND DIFFERENTIAL PRESSURE
In this Appendix, we prove Equations (18)–(24) which give the energy dependence of ENA flux and differential pressure, as well as their maximum energy. Starting from the ENA flux (Equation (B2)) and substituting the kappa distribution of protons (Equation (C2)), we derive
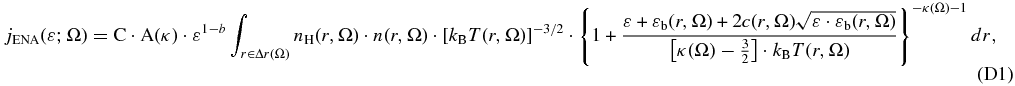
where the flux jENA is given in cm-2 s-1 sr-1 keV-1, the densities nH and n in cm-3, the heliocentric distance r in AU, the energies ε and kBT in keV, and the constant C as given by Equation (B10). In addition, c ≡ −cos (ω), where ω defines the orientation angle between the velocity of a proton  and the bulk velocity
and the bulk velocity  (both velocities given in the heliospheric inertial reference frame); ε ≡ 1/2m · u2; εb ≡ 1/2m · u2b. The reasonable range of angle ω in the inner heliosheath is 900 ⩽ ω ⩽ 1800, or 0 ⩽ c ⩽ 1.
(both velocities given in the heliospheric inertial reference frame); ε ≡ 1/2m · u2; εb ≡ 1/2m · u2b. The reasonable range of angle ω in the inner heliosheath is 900 ⩽ ω ⩽ 1800, or 0 ⩽ c ⩽ 1.
Using the radial means over the inner heliosheath thickness Δr (Section 2), Equation (D1) is rewritten as
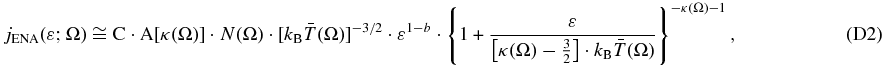
or
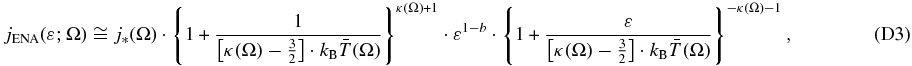
where the 1 keV flux, j*, is given by
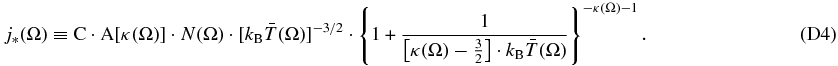
Equations (D3) and (D4) may reduce to linear spectra for ![$[\kappa (\Omega) - {{3 / 2}}] \cdot k_{\rm B} \bar T(\Omega) \ll 1\,{\rm keV}$](https://content.cld.iop.org/journals/0004-637X/762/2/134/revision1/apj453971ieqn149.gif) , as given by Equations (2) and (3), respectively.
, as given by Equations (2) and (3), respectively.
The maximum of the energy-flux spectrum is given by the derivative of Equation (D1), ∂jENA(ε; Ω)/∂ε = 0, which after some calculus can be written as
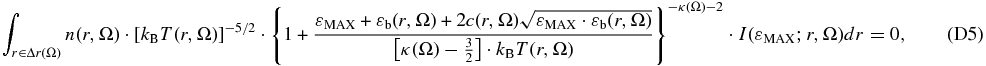
with

where nH(r, Ω)≅nH(Ω) and so it is canceled out of the integral. The spectrum maximum is located at smaller energy than the high energy asymptotic power-law of the IBEX-Hi energy range, εMAX ≪ (κ − 3/2)kBT. In addition, the bulk energy in the inner heliosheath is typically smaller than the thermal energy, εb ≪ (κ − 3/2)kBT. Hence, Equation (D2) becomes
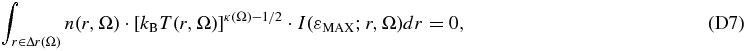
which gives
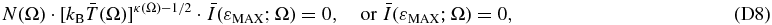
where the mean bar denotes the radial mean over the inner heliosheath thickness Δr (as explained in Section 2). Finally, applying Equation (D5) in Equation (D3) for εMAX, εb ≪ (κ − 3/2)kBT, we end up with
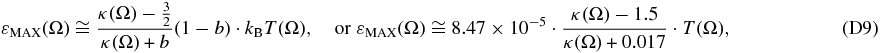
where we included the dependence of εMAX on the direction Ω; εMAX is in eV and T in K. If using the spectral index γ, instead of κ, then
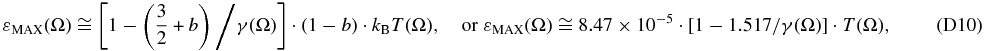
because of Equation (3), γ(Ω)≅κ(Ω) + b, with b≅0.017 ± 0.016.
Furthermore, the differential normalized partial pressure (averaged over the inner heliosheath thickness), or shortly, differential pressure, JP, can be defined by
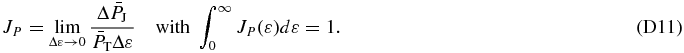
This can be derived from Equation (B14),
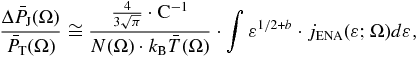
i.e.,
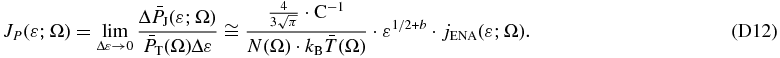
Then, by substituting jENA from Equation (D1) in Equation (D9), we derive
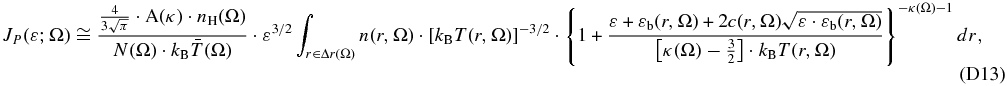
or, considering the radial means in the inner heliosheath (Section 2),
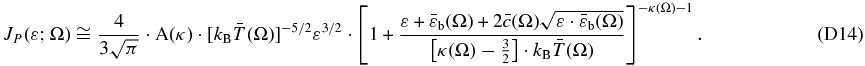
Moreover, εb ≪ (κ − 3/2)kBT, so that Equation (D14) is approximated to
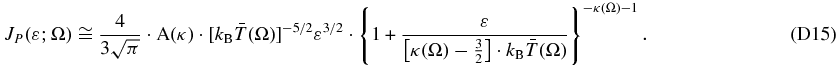
The energy εMAX that maximizes the differential pressure can be calculated similar to the derivation of the ENA flux maximum in Equation (D9). Comparing Equations (D3) and (D15), we easily conclude that the maximum of JP is
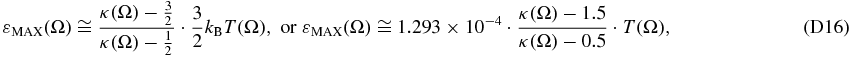
For example, for κ ≈ 1.7,  , we have
, we have  , and
, and