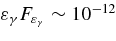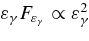ABSTRACT
We investigate hypernova (hyper-energetic supernova) and gamma-ray burst (GRB) remnants in our Galaxy as TeV gamma-ray sources, particularly in the role of potential TeV unidentified sources, which have no clear counterpart at other wavelengths. We show that the observed bright sources in the TeV sky could be dominated by GRB/hypernova remnants, even though they are fewer than supernova remnants (SNRs). If this is the case, TeV SNRs are more extended (and more numerous) than deduced from current observations. In keeping with their role as cosmic ray accelerators, we discuss hadronic gamma-ray emission from π0 decay, from β decay followed by inverse Compton emission, and propose a third novel process of TeV gamma-ray emission arising from the decay of accelerated radioactive isotopes such as 56Co entrained by relativistic or semi-relativistic jets in GRBs/hypernovae. We discuss the relevant observational signatures which could discriminate between these three mechanisms.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Observations at a new wavelengths have always led in astronomy to new discoveries, such as radio pulsars, gamma-ray bursts (GRBs), etc. The TeV gamma-ray sky is likely to yield similar surprises, since among the rapidly growing number of TeV sources (Aharonian et al. 2006) the most abundant category is of a mysterious nature, the so-called TeV unidentified sources (TeV unIDs), which have no clear counterpart at other wavelengths (Aharonian et al. 2005, 2008; Mukherjee & Halpern 2005). Our knowledge of TeV unIDs is very limited:
- 1.So far NunID ∼ 10–30 TeV unIDs have been observed.
- 2.They generally lie close to the Galactic plane, suggesting a Galactic origin.
- 3.They are extended, ΔΩ ∼ 0.05–0
 3.
3. - 4.The flux is
 –10−11 erg s−1 cm−2 at εγ ∼ 0.2 TeV.
–10−11 erg s−1 cm−2 at εγ ∼ 0.2 TeV. - 5.They have a power-law spectrum with an index of 2.1–2.5.
- 6.
The high energy nature of TeV unIDs naturally leads us to consider the cosmic ray (CR) accelerators as their possible origin. Since the dominant CR sources are supernova remnants (SNRs), TeV unIDs may be related to SNRs, in particular old ones, which are expected to be less luminous at other wavelengths (Yamazaki et al. 2006). However, the required galactic energy budget of TeV unIDs is only
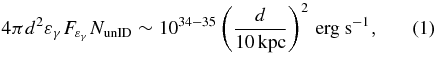
which is much less than that of supernovae (SNe),
implying a rarer type of source.
Long GRBs are actually rare SNe endowed with relativistic jets, which also are expected to leave SNR-like remnants (Perna et al. 2000; Ayal & Piran 2001). Even so, the expected number of GRB remnants is so small that previous works have addressed only specific sources (Ioka et al. 2004; Atoyan et al. 2006). However, recent observations suggest that hyper-energetic SNe, the so-called hypernovae which are sometimes associated with GRBs, such as SN1998bw/GRB980425, SN2003dh/GRB030329, and SN2003lw/GRB031203 (Maeda & Nomoto 2002), occur more frequently than GRBs (Guetta & Della Valle 2007). The hypernova rate may be even higher if we are missing GRB-unassociated hypernovae like SN1997ef. On the other hand, a larger fraction of SNe may be endowed with slower or semi-relativistic jets, causing only low-luminosity (LL) GRBs. Actually, a significant energy ∼1050 erg was released in the form of a mildly relativistic ejecta in the very faint GRB980425/SN1998bw. The recently discovered LL GRB060218/SN2006aj could also be produced by a slower or semi-relativistic jet (Toma et al. 2007; Waxman et al. 2007), occurring at a ∼10 times higher rate than GRBs (Guetta & Della Valle 2007; Liang et al. 2007; Soderberg et al. 2006c). Such semi-relativistic jets could be intermediate between choked and breaking-out jets emerging through the progenitor's outer envelope.
An interesting point in TeV unIDs is that their emission may be related to hadronic processes, since a simple leptonic process for TeV gamma rays by inverse Compton (IC) would require too much synchrotron emission than that is observed in TeV unIDs. Therefore, we consider the hadronic processes associated with the π0 decay (Section 2.1) for the hypernova shocks, and with the β-decay mechanism (Section 3.1), as well as a new mechanism of accelerated radio-isotope (RI) decay (Section 3.2) for the GRB jets. In the RI decay model, TeV gamma rays are produced by the Lorentz boosting of the MeV decay gamma rays of accelerated RI, such as 56Co entrained by the jets. To our knowledge, this is the first discussion of the decay of accelerated RI as a mechanism for generating TeV gamma rays in astrophysical sources. In this case, the source of the gamma-ray energy is injected initially at the base of the jet. There is no need for target matter or photons, as in the usual processes such as the π0 decay, IC, or photodisintegration (Anchordoqui et al. 2007).
In this paper, we investigate the high energy implications of GRB/hypernova remnants for TeV sources, in particular for TeV unIDs. Even though the total number of GRB/hypernova remnants is less than that of SNRs, the observed number in the TeV sky could be larger (Section 2.1). This in turn predicts more extended (and more numerous) TeV SNRs than currently observed, which may be discovered by expanding the search region even with the current instruments. We use the units kB = h = 1 and Qx = Q/10x in cgs units unless otherwise stated.
2. HYPERNOVA SHOCKS
2.1. π0 Decay Model
The simplest and most plausible process for TeV gamma-ray emission associated with CRs is the π0 decay from pp interactions between the interstellar medium (ISM) and CRs accelerated by the SN/hypernova shocks. Although the π0 decay for SNRs (Naito & Takahara 1994; Drury et al. 1994) and GRB remnants (Atoyan et al. 2006) has been discussed in detail, there are few works dealing with π0 decay in hypernova remnants, except for the specific source HESS J1303-631 (Atoyan et al. 2006). Since hypernovae are more energetic than SNe and GRBs and more frequent than GRBs, it is worth considering their implications for TeV unIDs.
By scaling the SNR calculation (Naito & Takahara 1994; Drury et al. 1994), we obtain a TeV gamma-ray flux
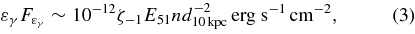
comparable to the observed values. Here, n is the ISM density in cm−3, d10 kpc = d/10 kpc, and ζ is the fraction of the total CR energy E per logarithmic energy interval. Since the kinetic energy of hypernovae is huge, Ek ∼ 1052 erg, a CR energy of E ∼ 1051 erg is reasonable, for a conventional CR acceleration efficiency of ∼10%.
Since the flux in Equation (3) is independent of time, most sources are likely old, e.g., tage ∼ 105 yr old. Such old SNRs are possible TeV unIDs because the maximum energy of primary electrons is so small that the leptonic emission is suppressed. As shown in Figure 1, the synchrotron emission from secondary electrons can also be below upper limits for TeV unIDs in the radio to X-ray bands (Yamazaki et al. 2006; Atoyan et al. 2006).
Figure 1. Flux from the π0 decay via pp interactions between the ISM and CRs accelerated by the hypernova shocks, compared with the Fermi and HESS sensitivities. We assume a remnant of age tage = 105 yr at d = 10 kpc with a CR energy E = 3 × 1051 erg and the CR spectral index p = 2.2 in the energy range mpc2 < εp < 105mpc2. We also show the synchrotron emission from π0 decay positrons and electrons for B = 3 μG, compared with the observational upper limits for an X-ray to TeV flux ratio of 10−2 and a radio to TeV flux ratio of 10−3. We use a code of Kamae et al. (2006) for calculating pp interactions. In addition, we also plot the bremsstrahlung, synchrotron, and IC emission from primary electrons with the spectral index p = 2.2 and the electron-to-proton ratio of (e/p)10 GeV ∼ me/mp at 10GeV.
Download figure:
Standard image High-resolution imageRemarkably, the observed number of old hypernova remnants may be comparable to that of the more numerous old SNRs, if the observations are flux-limited. For old remnants, which are larger than the angular resolution (see Equation (8)), the source size should be taken into account. As the search region is expanded, more background is included. The sensitivity is proportional to the inverse square of the background, for background-dominated counting statistics. Therefore, the flux sensitivity to an extended source with a physical radius r is given by  , where
, where  is the sensitivity to a point source and θcut is the angular cut in the analysis (Konopelko et al. 2002; Lessard et al. 2001). With Equation (3), and
is the sensitivity to a point source and θcut is the angular cut in the analysis (Konopelko et al. 2002; Lessard et al. 2001). With Equation (3), and
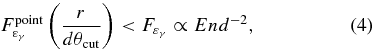
we have the maximum distance to a source as

and hence the observable volume in the Galactic disk is
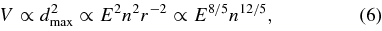
where we use r ∝ E1/5n−1/5t2/5age, which is approximately correct even for the radiative phase of the remnants. Since the hypernova energy is ∼10 times larger, the observable number of hypernova remnants is larger than that of SNRs by
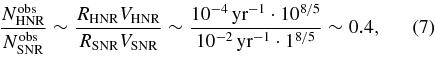
where RSNR ∼ 10−2 yr−1 and RHNR ∼ 10−4 yr−1 (∼7% of the SNe Ibc rate) are the event rates of SNe and hypernovae, respectively (Guetta & Della Valle 2007), and we assume a similar age tage and ISM density n for both remnants. The actual numbers in our Galaxy would be RSNRtage ∼ 103 (SNRs) and RHNRtage ∼ 10 (hypernova remnants) for tage ∼ 105 yr. Since the observed number of TeV unIDs is also ∼10, we may be reaching the farthest hypernova remnants in our Galaxy.
The angular size of the tage ∼ 105 yr old remnants,
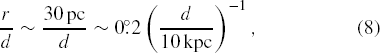
is consistent with TeV unIDs for hypernovae,3 but the same may not be true for SNe since the observable distance dmax is smaller and hence the angular size is more extended (r/d ∼ 2°(1 kpc/d)). Such an extended object can be found only if the search region is expanded to the degree scale in the analyses. Therefore, if TeV unIDs are hypernova remnants, we can predict more extended (and more numerous) TeV SNRs than observed, which may be discovered by expanding the search region even with the current instruments.
The flux of hypernova remnants could be further enhanced if the density n is higher around hypernovae than around usual SNe. The GRBs and SNe Ic, which are the only type of core collapse SNe associated with GRBs and hypernovae, are far more concentrated in the very brightest regions of their host galaxies than are the other SNe (Kelly et al. 2008; Fruchter et al. 2006), suggesting that GRBs and hypernovae are associated with star-forming regions with high density. Conversely, hypernovae could be runaway massive stars ejected several hundreds of parsec away from high density stellar clusters (Hammer et al. 2006). In this case, no flux enhancement is expected.
It is necessary to check any possible side effects of this mechanism at other wavelengths which might violate the hypothesis that they remain unidentified. In particular, we need to check what is the possible X-ray emission from electrons in these sources. We may constrain the electron acceleration in the old hypernova remnants. In Figure 1, we have plotted the bremsstrahlung, synchrotron, and IC emission from primary electrons with the same spectral index p = 2.2, for an electron-to-proton ratio of (e/p)10GeV ∼ me/mp ∼ 10−3 at 10 GeV. The radio observations limit the (e/p)10GeV ratio to ≲10−3, which is somewhat smaller than the observations ∼0.02. Note however that the injection of thermal electrons into the acceleration process is poorly understood, and the observed electron CRs might be produced by other sources such as usual SNRs or pulsars. In any case, the leptonic model for TeV unIDs seems unlikely. Note that we take the Coulomb losses for low energy electrons into account according to Uchiyama et al. (2002) (see also Baring et al. 1999) and this makes the bremsstrahlung spectrum hard in the X-ray band. On the other hand, the thermal bremsstrahlung emission is not bright in the X-ray band, in contrast with the usual young SNRs (Katz & Waxman 2008), because the temperature of old SNRs is much below the X-ray energy, T ∼ 0.04 keV E2/5k,52n−2/5(t/105 yr)−6/5 (Reynolds 2008).
3. GRB JETS
3.1. β Decay Model
A fraction of SNe/hypernovae is associated with long GRB and their jets. Another process for generating TeV gamma-rays is the (time-delayed) β decay of the neutron component of the CR outflow accelerated by the jets followed by IC scattering (Ioka et al. 2004). We have applied this process to the SNR W49B (G43.3-0.2), which is a possible GRB remnant (Keohane et al. 2006; Miceli et al. 2006, 2008). Since the β decay can occur outside the remnant, the jet-like emission would appear outside of the SNR. Note that the GRB-associated SNe are not necessarily energetic hypernovae since the luminosity distribution of GRB-associated SNe is statistically consistent with that of local SNe Ibc (Soderberg et al. 2006b).
As shown in Figure 2, old jet remnants with tage ∼ 105 yr are potentially TeV unIDs since the usual SNR emission goes down at this age, while electrons that emit ∼TeV gamma rays (i.e., γe ∼ 107 electrons) need tcool ∼ 105 yr to cool (see Equations (3) and (4) in Ioka et al. 2004). (However a spectral cutoff at ∼10 TeV may be seen at this age.) Then the expected total number is 0.1–1 for a Galactic GRB rate of ∼10−5–10−6 yr−1 (Guetta & Della Valle 2007). The actual number would be larger because a larger fraction of SNe may have lower-luminosity jets that were not identified (e.g., Toma et al. 2007), and LL jets can also accelerate CRs to energy ∼1016-17 eV (e.g., Murase et al. 2006, 2008), which is necessary for the TeV gamma-ray emission. The most optimistic rate consistent with the late-time radio observations is ∼10−4 yr−1 (∼10% of the SN Ibc rate) (Soderberg et al. 2006a), yielding a total number of ∼10, comparable to that of TeV unIDs. All of these remnants could be detected, i.e., dmax ∼ 10 kpc, if the total energy in accelerated CRs is comparable to the typical GRB energy.
Figure 2. Flux from the IC scattering of CMB photons by the β-decay electrons via the CR neutron component in the GRB jets, compared with the Fermi and HESS sensitivities. We assume a remnant of age tage = 105 yr at d = 10 kpc with a CR energy E = 3 × 1051 erg (i.e., an old remnant version of Model (I) in Ioka et al. (2004)) and a CR Lorentz factor 106 < γn < 109. We also show the synchrotron emission from β-decay electrons for B = 3 μG, compared with observational upper limits for an X-ray to TeV flux ratio of 10−2 and a radio to TeV flux ratio of 10−3.
Download figure:
Standard image High-resolution image3.2. Radio-isotope (RI) Decay Model
The chemical composition of jets which may be associated with SNe/hypernovae is currently unknown. One interesting possibility is that they entrain radioactive isotopes, in particular 56Ni and 56Co. The SN/hypernova shock leads to explosive nucleosynthesis, predominantly forming 56Ni via complete silicon burning (Maeda & Nomoto 2003). The inner 56Ni would fall back onto the central engine (in those objects where there is one), and a fraction of accreted 56Ni could be ejected with the ensuing jet. The photodisintegration of heavy nuclei would be suppressed in the LL jets whose temperature is less than ∼MeV. Even if heavy nuclei may disintegrate in the innermost accretion disk, 56Ni could be produced again in a cooling wind (MacFadyen 2003). 56Ni could be also entrained into the jet from the surroundings. The subsequent photodisintegration can be avoided in large fraction of parameter space (Wang et al. 2008; Murase et al. 2008). The spectrum and light curve modeling of GRB-associated hypernovae suggests that the total amount of 56Ni is larger than that in ordinary SNe and heavy elements are aspherically ejected along the jet direction (Maeda & Nomoto 2002).
56Ni decays into 56Co in tNiln 2 = 6.1 days essentially by electron capture (McLaughlin & Wijers 2003). The decay proceeds primarily through the excited states of 56Co, emitting ∼2 MeV gamma rays. 56Co also decays primarily by electron capture into excited 56Fe with a half-life of tColn 2 = 77.2 days,
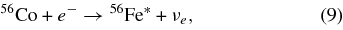
followed by εRI ∼ 2 MeV gamma-ray emission
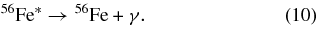
If the nuclei are fully ionized, they decay by emission of a positron (β+ decay), e.g.,

followed by gamma-ray emission, since free electron capture is negligible in our case. The half-life for ionized 56Co is a factor of ∼5 higher than for 56Co with electrons, while that of ionized 56Ni is longer than 3 × 104 yr. Since nuclei can recombine in an expanding jet (McLaughlin & Wijers 2003), the decay chain 56Ni → 56Co → 56Fe can start from the 56Ni electron capture.
The outflowing jet is shocked as it interacts with the ISM, leading to particle acceleration. Unlike in the ordinary SNe, the RI acceleration can occur before the RI decay in the objects considered here, involving jets reaching relativistic speeds. Our interest is in the 56Co acceleration, since the accelerated nuclei are completely ionized and the ionized 56Ni is essentially stable (the half-life is longer than 3 × 104 yr). For the 56Co acceleration, the shock radius should be smaller than the 56Co decay length, r < ctCo(ln 2)βΓ and larger than the 56Ni one, r > ctNi(ln 2)βΓ, where Γ is the Lorentz factor of the jet. Since the shock radius may be estimated by Ej ∼ (4π/3)r3nmpc2β2Γ2, we have
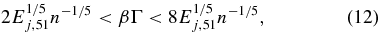
where Ej is the total energy of the jet. The Lorentz factor ranges between that of GRBs and hypernovae. Note that the shock radius is relatively large ≳1016 cm that no heavy nuclei may disintegrate (Murase et al. 2008; Wang et al. 2008).
Once 56Co is accelerated, the observed mean lifetime is extended by the Lorentz factor,
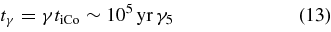
enabling long-lasting emission, where tiCo = 5tCo is the half-life of ionized 56Co. The observed energy of the decay gamma rays is also Lorentz-boosted to
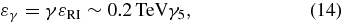
potentially applicable to TeV unIDs. The ratio of gamma-ray energy to the 56Co CR energy is about f = εRI/56mpc2 ∼ 4 × 10−5. The gamma-ray flux is then estimated as
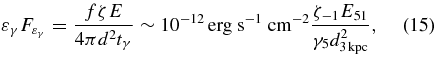
interestingly comparable to that of TeV unIDs, where d3 kpc = d/3 kpc and E is the total energy of 56Co CRs. In a sense, this is a relativistic version of the SN emission since the energy source is the RI decay.
In the RI model, a similar way to the β-decay model, the total source number is 0.1–1 for a Galactic GRB rate of ∼10−5–10−6 yr−1 (Guetta & Della Valle 2007), while the most optimistic number is ∼10 for a rate consistent with the late-time radio observations ∼10−4 yr−1 (∼10% of the SN Ibc rate) (Soderberg et al. 2006a). We can detect a fraction ∼(3 kpc/10 kpc)2 ∼ 0.1 of these sources, if CRs comprise an energy comparable to the typical GRB energy. For a rare event with high energy and/or with reacceleration by the hypernova shock, the observable distance may be farther.
We note that other RI species may also contribute. In particular, the 57Ni emission via β+ decay dominates in the young (∼103 yr) remnants because its half-life 35.6 hr is ∼102 times shorter than 56Ni though its yield is less by 0.1–0.01 (Maeda & Nomoto 2002, 2003).
The shocked 56Co is accelerated to a power-law spectrum dNCo ∝ ε−pCodεCo for εCo < εCo,max. The maximum energy can be εCo,max ∼ 3 × 1017 eV (e.g., Murase et al. 2008), which provides εγ,max ∼ f × (3 × 1017eV) ∼ 10 TeV decay gamma ray. Hereafter, we adopt this maximum energy. The Larmor radius of 56Co CRs is ∼4(εCo/1017eV)B−1−6 pc, leading to the isotropic emission of decay gamma rays.
As shown in Figure 3, the decay gamma rays have a unique spectrum,
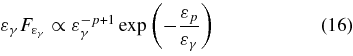
with an exponential cutoff4 below
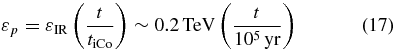
and a power law above it, where the power-law index is softer than that of parent CRs by 1. This is because the low energy CRs have already decayed while the high energy CRs are decaying with a rate (d/dt)exp(−t/γtiCo) ∝ ε−1γexp(−εp/εγ). The spectrum of TeV unIDs is characterized as a power law with index 2.1–2.5 (Aharonian et al. 2008), which corresponds to p = 1.1–1.5 in Equation (16). This is slightly harder than the p = 2 expected in the test particle acceleration case. The harder spectrum could suggest nonlinear shock effects in jets where the CR pressure is nonnegligible (Ellison 2001). This is consistent with the fact that the necessary CR energy is comparable to the total energy of jets, E ∼ Ej.
Figure 3. Flux of the decay gamma rays from accelerated RI 56Co CRs in Equations (10), (15), and (16), compared with the Fermi and HESS sensitivities. We assume a remnant of age tage = 105 yr at d = 3 kpc with a CR energy E = 3 × 1051 erg and spectral index p = 1.5. We also show the synchrotron and IC emission from decay positrons given by Equation (11) for B = 3 μG and the CMB, compared with observational upper limits for an X-ray to TeV flux ratio of 10−2 and a radio to TeV flux ratio of 10−3.
Download figure:
Standard image High-resolution imageIn Figure 3, we also show the synchrotron and IC emission from decay positrons in Equation (11), which have an energy comparable to that of decay gamma rays. The positron spectrum is dNe ∝ ε−pedεe for Γmec2 < εe < εp and dNe ∝ ε−p − 1edεe for εp < εe < εmax . The synchrotron frequency is νsyn = qBε2e/2πm3ec5 ∼ 10−4B−6(εe/0.1TeV)2 eV while the IC frequency is νIC ∼ 9 CMB(εe/mec2)2 ∼ 108(εe/0.1TeV)2 eV, where we consider cosmic microwave background (CMB) as main target photons (Ioka et al. 2004).
CMB(εe/mec2)2 ∼ 108(εe/0.1TeV)2 eV, where we consider cosmic microwave background (CMB) as main target photons (Ioka et al. 2004).
However, the cooling time tc = 3m2ec3/4σTεeU ∼ 107(εe/0.1TeV)−1U−1−12 yr is usually longer than the decay time tγ in Equation (13) for εe < εmax ∼ 10 TeV, where U is the total energy density of magnetic fields and CMB. Then the luminosity is suppressed by tγ/tc ∼ 10−2(tγ/105 yr)(εe/0.1TeV)U−12 compared with decay gamma rays in Equation (15). This is favorable for the interpretation of such sources as TeV unIDs. Note that the ∼eV photons by decay positrons come from an extended region in which the optical background dominates the remnant flux.
The accelerated RI CRs may suffer the adiabatic energy losses during the expansion of the remnant (Rachen & Mészáros 1998), which will greatly suppress the RI emission. This is a potential problem for the RI decay model. However, the CR escape from a remnant is not fully understood yet. For instance, it is common to assume the free escape of CRs in models where the GRB reverse shocks are the sites for the ultra high energy CR production (e.g., Waxman 2006; Murase et al. 2008). In the same sense, the RI decay model is a viable possibility for TeV unIDs.
4. DISCUSSION
We have discussed the TeV gamma-ray emission from the π0 decay, β-decay, and the RI decay mechanisms in GRB and/or hypernova remnants, in their possible role as TeV unIDs. There is evidence that typical GRBs predominantly occur in galaxies with less metals than our own (Fruchter et al. 2006; Stanek et al. 2006), although the correlation between the host metallicity and the GRB energy is not confirmed (Savaglio et al. 2009, 2008). On the other hand, broad-lined SNe Ic also inhabit more metal-rich galaxies (Modjaz et al. 2008), suggesting that at least hypernovae and possibly GRB/SNe with LL jets can occur in our Galaxy. In addition, the evidence that GRBs occur in low metal regions could be biased because the GRBs in the metal-rich region tend to have no optical afterglows due to the dust absorption (i.e., dark GRBs, which is about half of all GRBs). Then it becomes difficult to identify the hosts for measuring the metal abundance.
To discriminate amongst these models, the imaging of the gamma-ray morphology would be useful. The π0 decay model predicts a shell structure, since the density inside the remnants is low, while the β-decay model predicts an elongated structure, and the RI decay model predicts a center-filled structure. For remnant ages tage < 105 yr, the SNR may be observed also at other wavelengths. HESS J1731-347 may be such an example, which is likely to be an old SNR with a large gamma ray to radio flux ratio FTeV/Fradio ∼ 33 (Tian et al. 2008). HESS J1834-087 may be also an old remnant with an elongated gamma-ray emission outside the SNR (Aharonian et al. 2006), which could be interpreted in the context of a β-decay model (but see also Mukherjee et al. 2009).
The π0 decay model predicts detectable GeV emission if the spectral index of 2.1-2.4 continues down to the GeV region (see Figure 3). Other models predict relatively low levels of GeV emission (Figure 3; Ioka et al. 2004; Yamazaki et al. 2006; Atoyan et al. 2006), although rare young remnants may be bright if εp ∼ 20 GeV(t/104 yr) in the RI model. This may be tested by the Fermi satellite. Note that the GRB prompt and afterglow emission will mask the very early RI decay emission, which becomes prominent later.
The implied TeV neutrino flux (∼ gamma-ray flux) is not enough for detection by current facilities. However, in the future one may in principle test models through the flavor ratio. We expect  in the π0 decay model, no neutrinos in the β-decay model (since neutrinos are beamed and usually off-axis), and 56Co → 56Fe* + e+ + νe in the RI decay model.
in the π0 decay model, no neutrinos in the β-decay model (since neutrinos are beamed and usually off-axis), and 56Co → 56Fe* + e+ + νe in the RI decay model.
As discussed at the end of Section 2.1, the radio observations limit the (e/p)10GeV ratio to ≲10−3 in the π0 decay model. For the RI decay model, the CRs need to freely escape from the acceleration site before suffering the adiabatic energy losses (see the end of Section 3.2).
The implied CR energy budget is less than ∼10% ∼ (10 times energy) × (10−2 times rate) of the standard SN CR energy budget in our models. The CRs above the knee at ∼3 × 1015 eV, however, could be produced mainly by extragalactic and/or Galactic GRBs/hypernovae (Wick et al. 2004; Murase et al. 2006; Wang et al. 2007; Budnik et al. 2008). The chemical composition is increasingly richer in heavy nuclei above the knee ∼3 × 1015 eV to the second knee ∼6 × 1017 eV (Antoni et al. 2005; Abbasi et al. 2005), and possibly above ∼3 × 1019 eV (Unger et al. 2007). These may be accelerated by jets as in the RI decay model.
The GRB remnants may be also responsible for the excesses of CR positrons and electrons recently observed by the PAMELA and ATIC/PPB-BETS experiments (Ioka 2008; Fujita et al. 2009). Since the electron and positron sources should be nearby (less than ∼1 kpc away), it may be difficult to detect these sources by gamma rays.
Recently, wide-field optical surveys have been discovering exceptionally luminous SNe, such as SN 2005ap, SN 2008am, SN 2006gy, SN 2006tf, and SN 2008es (Miller et al. 2009). The SN 2008es yields a radiated energy of ≳1051 erg and possibly a total energy of ∼1052 erg, comparable to the hypernova energy. The rate could be also comparable to the hypernovae rate although only an upper limit to the rate is obtained (Miller et al. 2009). Therefore such luminous SNe could also become TeV unIDs like the hypernova case, although the luminous SNe are type II and may not be related to GRBs.
In conclusion, we propose that GRB/hypernova remnants are promising candidates for the TeV unIDs. If TeV unIDs are hypernova remnants, we can predict more extended (and more numerous) TeV SNRs than observed, which may be discovered by expanding the search region to larger angular scales, even with the current instruments. We also propose a new process of TeV gamma-ray emission involving the decay of accelerated radioactive isotopes, such as 56Co entrained by relativistic or semi-relativistic jets in GRBs/hypernovae.
We thank T. Nakamura, T. Kamae, S. Razzaque, S. Inoue, R. Mukherjee, C. Dermer, R. Yamazaki, S. Park, and T. Mizuno for useful comments. This work is supported in part by the Grant-in-Aid from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan, No. 18740147, 19047004, 21684014 (K.I.), and NASA NNX08AL40G, NSF PHY-0757155 (P.M.).
Footnotes
- 3
The CR diffusion could increase the source size (Atoyan et al. 2006), although the diffusion coefficient has large uncertainties.
- 4
The actual cutoff is a power low
 for εγ < εp because nuclei also make off-axis emission outside the relativistic beaming angle (Ioka & Nakamura 2001). This does not change our results.
for εγ < εp because nuclei also make off-axis emission outside the relativistic beaming angle (Ioka & Nakamura 2001). This does not change our results.