THE INTERACTION OF ALFVÉN WAVES WITH PERPENDICULAR SHOCKS

Particle acceleration is a ubiquitous phenomenon at shock waves, and occurs on scales from supernova remnants to interplanetary shocks and cometary bow shocks. Diffusive shock acceleration is the mechanism considered to be responsible for the almost universally observed power-law spectra of energetic particles from cosmic rays to gradual solar energetic particle (SEP) events (Axford et al. 1977; Bell 1978; Blandford & Ostriker 1978). The theory of diffusive shock acceleration is successful in explaining SEP observations at quasi-parallel shocks (Zank et al. 2000; Li & Zank 2003). At a quasi-parallel shock, the upstream ions reflected by the shock stream far upstream along the magnetic field, and excite low-frequency plasma waves by plasma beam instabilities (Gary 1991; Lu et al. 2006). The waves make the ions to be scattered across the shock several times. In this way, these particles can be accelerated to very high energies, forming a power-law spectrum (Lee 1983; Zank et al. 2000, 2007; Li & Zank 2003; Giacaclone 2004). A similar theory does not work at quasi-perpendicular shocks. At a quasi-perpendicular shock, the reflected upstream ions return to the shock immediately due to the gyromotion of the particles in the magnetic field. So the excited waves by energetic particles are not generated in situ, thus limiting particle scattering (Wilkinson & Schwartz 1990; Gordon et al. 1999; Yang et al. 2009). These particles escape the shock rapidly. Therefore, it is difficult to accelerate particles to high energies and explain the observed power-law spectra of the energetic particles at quasi-perpendicular shock waves.

Recently, cross-field diffusion by large-amplitude intrinsic magnetic turbulence has been suggested to play an important role in particle acceleration at quasi-perpendicular shocks. Particles following irregular random walking magnetic fields are able to cross the shock repeatedly. In this way, particles can also be accelerated to high energies (Giacaclone 2005a, 2005b; Zank et al. 2006), and the observed power-law spectra of energetic particles at quasi-perpendicular shocks can be explained (Zank et al. 2006). Therefore, the interaction of upstream Alfvén waves (a proxy for solar wind turbulence) with a quasi-perpendicular shock plays an important role in particle acceleration at quasi-perpendicular shocks. The interaction of Alfvén waves with shocks has been investigated by many authors. With a small amplitude linear analysis, McKenzie & Westphal (1969) investigated the transmission of Alfvén waves through the Earth's bow shock, and found that the magnetic field of the transmitted Alfvén waves is about three times larger than that of the incident waves. McKenzie & Volk (1982) studied the interaction of the cosmic-ray-generated Alfvén waves with a parallel shock, and found that one of the modified slow magnetoacoustic waves is unstable. Webb et al. (1999) derived equations describing the interaction of weakly nonlinear short-wavelength magnetohydrodynamics (MHD) waves with cosmic-ray-modified shocks. In these studies, the profiles of the shocks were fixed, and they were not affected by the Alfvén waves. Zank et al. (2002) considered a self-consistent approach in which the Rankine–Hugniot jump conditions are modified by turbulence, allowing for an approximately self-consistent solution. Finally, Ao et al. (2008) investigated the structural response of a MHD shock to upstream turbulence, finding that the shock can become distorted, sometime smoothed, with non-Rankine–Hugnoiot jumps in strength. In this paper, we use two-dimensional (2D) hybrid simulations to investigate the interaction of Alfvén waves with a perpendicular shock self-consistently. The amplification and characteristics of the transmitted Alfvén waves, as well as the modification of the shock front by the injected Alfvén waves, are investigated.

The paper is organized as follows. In Section 2, we describe the hybrid simulation model, The results are presented in Section 3, and in Section 4 the conclusions are given. Here relevant observations are presented and the implications to particle acceleration at quasi-perpendicular shocks are discussed.

In a hybrid simulation, ions are treated kinetically and electrons as a massless, charge-neutralizing fluid (Winske 1985). It is a well-known self-consistent plasma simulation method that has been used extensively to study the space plasma. In this paper, the plasma consists of proton and electron components, and the two-dimensional hybrid simulations are performed in the x–y plane. Initially, protons satisfy a Maxwellian velocity distribution with a drift speed along the x-direction, and a uniform background magnetic field ${\bf B}_0 = B_0 {\bf \hat y}$ (where ${\bf \hat y}$ is the unit vector along the y-direction) is assumed to be along the y-direction. Particles are injected from the left boundary with a speed of V_b = 4.0V_A (where $V_A = B_0 /\sqrt {\mu _0 m_p n_0 }$ is the Alfvén speed based on the upstream magnetic field B₀ and number density n₀, and m_p is the mass of the proton), and the plasma beta upstream of the shock is β_p = 2μ₀p₀/B²₀ = 0.5 (where p₀ is the upstream pressure). The number of grid cells is n_x × n_y = 600 × 256, and the grid sizes are Δx = 0.512c/ω_pp and Δy = 1.0c/ω_pp(where c/ω_pp = V_A/Ω_p is the proton inertial length and $\omega _{{\rm pp}} = \sqrt {n_0 e^2 /m_p \varepsilon _0 }$ is the proton plasma frequency based on the upstream number density n₀). The time step is Ω_pt = 0.02 (where Ω_p = eB₀/m_p is the proton gyrofrequency based on the upstream magnetic field B₀). To form the shock, we reflect the plasma at a rigid right boundary wall at x = x_right. A shock propagating to the left is formed. Periodic boundary conditions for the particles and fields are used in the y-direction.

We describe here three case studies: (1) one with no injected upstream Alfvén waves, (2) a case with a single monochromatic Alfvén wave injected from the left boundary and its wavelength is 64c/ω_pp, and (3) a simulation comprising a mixture of sinusoidal Alfvén waves injected from the left boundary, and their wavelengths are 85.33c/ω_pp, 64c/ω_pp, 51.2c/ω_pp, and 42.67c/ω_pp, respectively. The wavelengths for case (3) correspond to 1/3, 1/4, 1/5, and 1/6 of the domain size along the y-direction. The corresponding power spectrum of the waves has a Kolmogorov power-law index −1.667, which is a generally accepted value in the solar wind (Villante 1980; Bavassano & Smith 1986). In both cases (2) and (3), the injected Alfvén waves have the same wave amplitude ∑_kδB²_k/B²₀ = 0.25 in the left boundary, where k denotes the wave mode. Below, we describe the simulations for cases (2) and (3) first, and then compare them to case (1).

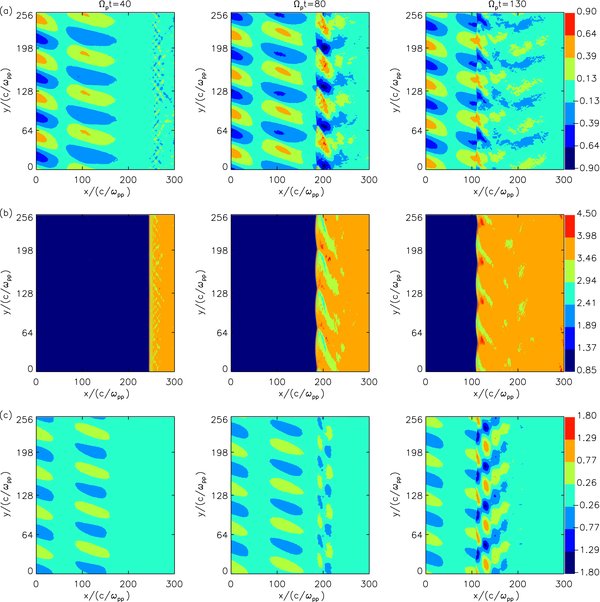
Figure 1 shows the distributions of the magnetic field components (a) B_x/B₀, (b) B_y/B₀, and (c) B_z/B₀ at Ω_pt = 40, 80, and 130 for case (2). The perpendicular shock propagates from the right boundary along the −x direction with a speed of about 1.5V_A and an average compression ratio of about 3.6. Considering that the upstream plasma drift along the +x direction with a speed of V_b = 4.0V_A, we can calculate that the shock Alfvén Mach number is 5.5. The downstream B_y is about 3–4 times that of the upstream, which is consistent with the MHD Rankine–Hugoniot relations. The monochromatic Alfvén wave injected at the left boundary is convected toward the shock. At about Ω_pt = 56, the Alfvén wave begins to interact with the shock. Obvious ripples can be found at the shock, which distort the shock front. The transmitted Alfvén wave experiences large amplification of the fluctuating magnetic fields B²_x and B²_z. The enhanced waves are then convected to far downstream slowly.

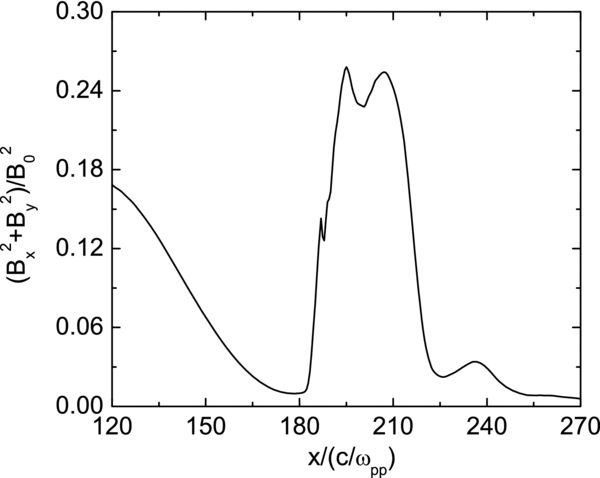
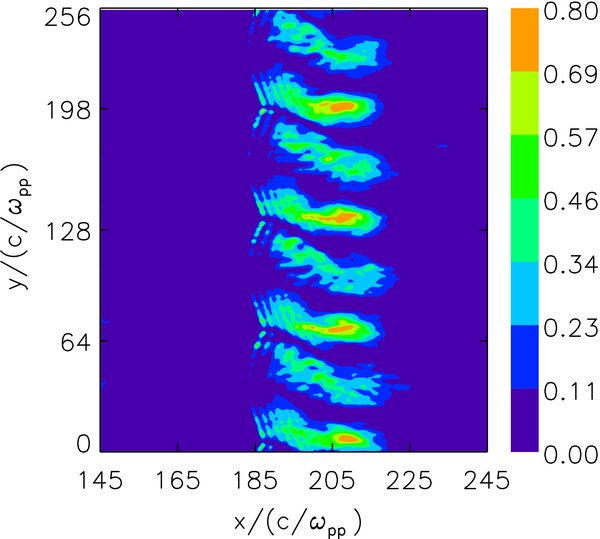
Zoom In Zoom Out Reset image size

The enhancement of the fluctuating magnetic field after transmission through the shock can be demonstrated more clearly in Figure 2, which shows the average of the fluctuating magnetic field (B²_x + B²_z)/B²₀ along the y-direction versus x at Ω_pt = 80 for case (2). The fluctuating magnetic field increases rapidly from about 0.015 just upstream of the shock to about 0.26 downstream of the shock. Therefore, the amplitude of the fluctuating magnetic field can be enhanced as large as about 17 times. There is no enhancement of the transmitting waves at the downstream region where the fluctuating magnetic field has not reached. Figure 3 shows the distributions of the amplitude of the fluctuating magnetic field (B²_x + B²_z)/B²₀ at Ω_pt = 80 for case (2). The enhancement of the fluctuating magnetic field B²_x + B²_z is different at different y positions, and at some positions the enhancement can be as large as 30 times.

Zoom In Zoom Out Reset image size

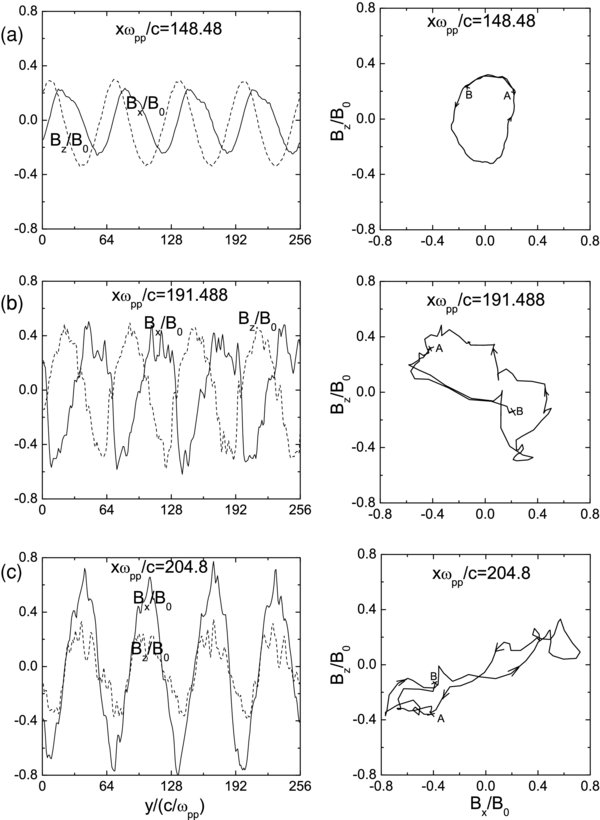
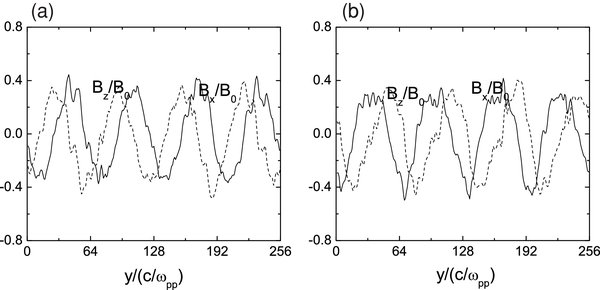
Zoom In Zoom Out Reset image size

To investigate the characteristics of the transmitted wave through the shock, we describe the polarizations of the wave at different positions. In Figure 4, the left panel shows the spatial profiles of the magnetic field B_x/B₀ and B_z/B₀ at Ω_pt = 80 for case (2). Three different positions at xω_pp/c = (a) 148.48, (b) 191.488, and (c) 204.8., which represent upstream, immediate downstream, and downstream, respectively, are chosen; the right panel shows the corresponding hodograph of B_x − B_z from A(yω_pp/c = 80) to B(yω_pp/c = 0). The Alfvén wave experiences obvious amplification after transmitting the shock. The upstream wave is left-hand circularly polarized, which propagates along the +y direction. When the wave transmits the shock, its polarization becomes elliptically polarized until nearly linearly polarized at xω_pp/c = 204.8. After separating the fluctuating magnetic field into positive and negative helical parts (Terasawa et al. 1986, Lu & Wang 2005), we find that the downstream fluctuating waves comprise two parts, and both of them are left-hand circularly polarized Alfvén waves: one propagates along the +y direction and the other along the −y direction. The amplitude ratios of these two parts (B²_x + B²_z)_+y/(B²_x + B²_z)_−y are about 3.06 and 0.95 at xω_pp/c = 191.488 and 204.8, respectively. Figure 5 displays the spatial profiles of B_x/B₀ and B_z/B₀ at Ω_pt = 80 for case (2), while (a) and (b) correspond to the parts propagating along the +y and −y directions at xω_pp/c = 204.8, respectively. Our simulation results are consistent with the linear theory of McKenzie & Westphal (1969); the upstream Alfvén wave is enhanced greatly after transmitting a shock due to the compression of the shock. Simultaneously, the transmitted waves through the shock are separated into two parts: one is the Alfvén wave propagating along the +y direction and the other along the −y direction.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Similar results are obtained for case (3), which comprises a mixture of sinusoidal Alfvén waves with wavelengths 85.33c/ω_pp, 64.0c/ω_pp, 51.2c/ω_pp, and 42.67c/ω_pp. Figure 6 shows the distributions of the magnetic field components (a) B_x/B₀, (b) B_y/B₀, and (c) B_z/B₀ at Ω_pt = 80 for case (3). Obvious ripples can be found at the shock front due to its interaction with Alfvén waves, and the ripples are not as regular as case (2). Again, we find that the amplitude of the fluctuating magnetic field ∑_kδB²_k is enhanced by a factor ranging from 10 to 50 after transmitting the shock.

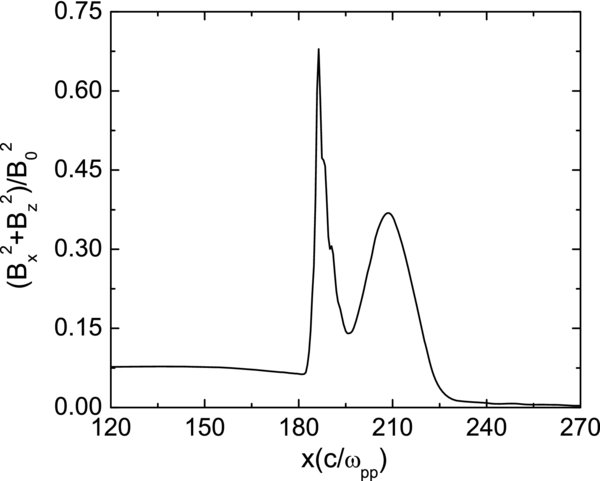
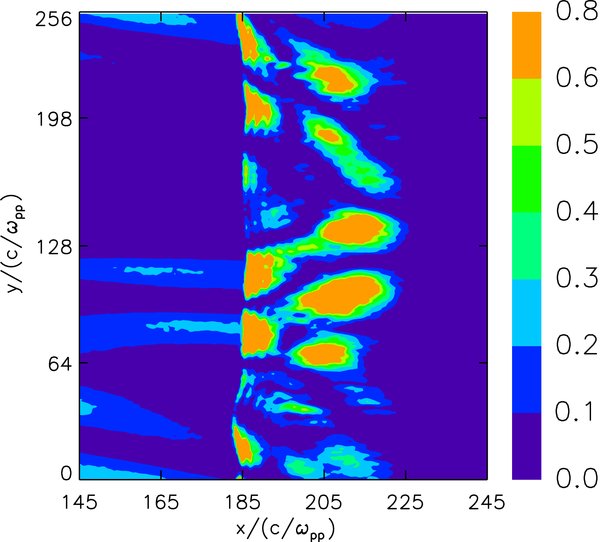
Zoom In Zoom Out Reset image size

Figure 7 describes the average of the fluctuating magnetic field ∑_kδB²_k/B²₀ = ∑_k(B²_x + B²_z)/B²₀ along the y-direction versus x at Ω_pt = 80 for case (3). The fluctuating magnetic field is enhanced from 0.07 just upstream of the shock to 0.63 just downstream of the shock, which is about nine times. The amplitude of the fluctuating magnetic field changes greatly. Figure 8 shows the distributions of the amplitude of the fluctuating magnetic field ∑_kδB²_k/B²₀ at Ω_pt = 80 for case (3). The enhancement of the fluctuating magnetic field B²_x + B²_z is also different at different y positions, and the enhancement can be as large as 50 times at some positions.

Zoom In Zoom Out Reset image size

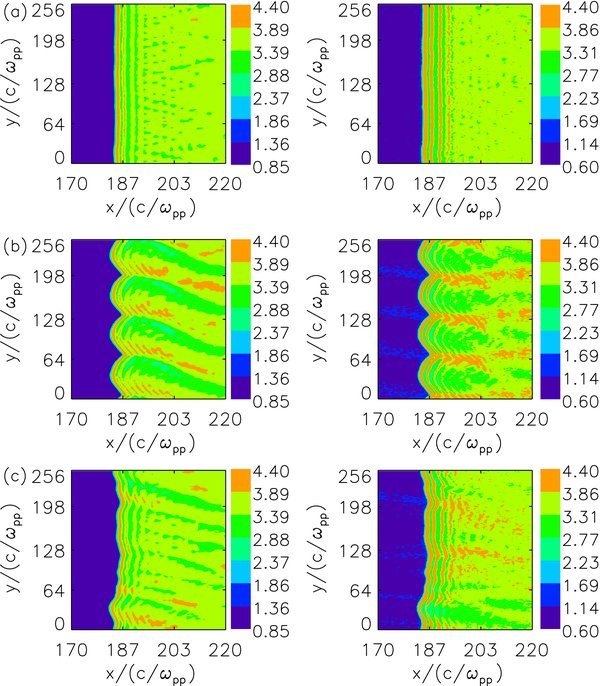
Zoom In Zoom Out Reset image size

In order to identify more clearly the effects of the Alfvén waves on the shock, we compare the structures of the shocks in different cases. Figure 9 describes the distributions of the magnetic field component B_y/B₀ (left panel) and the number density n/n₀ (right panel) at Ω_pt = 80 for three different cases: (a) is for case (1), while (b) and (c) are for cases (2) and (3). The shocks in these three cases are almost at the same location x = 185c/ω_pp, and it means that the injected Alfvén waves have no obvious influences on the propagating speed of the shocks. For the cases with the existence of the injected Alfvén waves, ripples at the shock front (both the magnetic field and number density) can clearly be identified. The ripples are consistent with the Alfvén waves in the upstream, and they propagate along the y-direction with the Alfvén waves in the upstream. Therefore, the ripples have a regular structure for the case with the monochromatic Alfvén wave, while the ripples for the case with a mixture of Alfvén waves are irregular.

Zoom In Zoom Out Reset image size

We also change the plasma beta and other parameters, and find that the enhancement of the upstream Alfvén waves is insensitive to these parameters. Although the enhancement of the fluctuating magnetic field in our hybrid simulations seems to be consistent with the predictions in McKenzie & Westphal (1969), we also find that the enhancement is different at different y positions. In addition, the polarization of the transmitted waves is changing when they are convected to far downstream.

In this paper, we used two-dimensional hybrid simulations to investigate the interaction of upstream Alfvén waves with a perpendicular shock. Upstream Alfvén waves have no obvious influence on the propagation speed of the shock, but structural modifications are clearly identified at the shock front. Furthermore, the amplitude of the Alfvén waves ∑_kB²_k is enhanced by a factor of some 10–30 after transmission. The transmitted waves can be separated into two parts, and both of them are left-hand circularly polarized Alfvén waves: one propagates along the +y direction and the other along the −y direction.

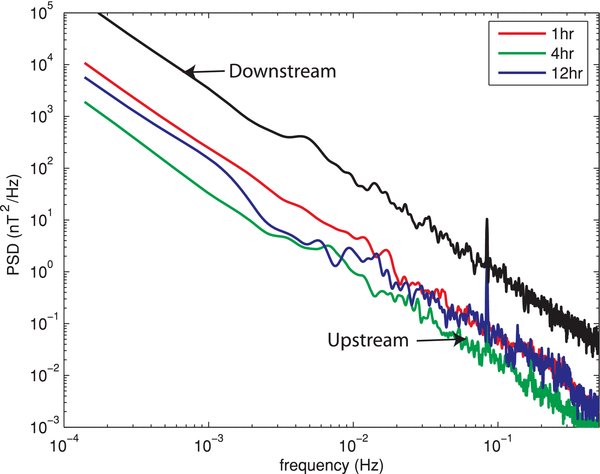
The enhancement of the amplitude of the Alfvén waves after transmitting the shocks can be verified by satellite observations of interplanetary shocks from the Advanced Composition Explorer (ACE). Figure 10 shows the magnetic field power spectral density (PSD) upstream (red, green, and blue lines) and downstream (black line) of such a shock, adapted from Zank et al. (2006), where the upstream PSDs were calculated for three intervals of increasing distances away from the shock. The PSD downstream was calculated for an interval immediately after the shock. The shock normal forms an angle of 92° ± 4° with an ambient upstream magnetic field. In upstream, no apparent enhancement of magnetic field fluctuations, often indicative of wave activities, is observed when the satellite approaches the shock. In downstream, the power of downstream fluctuations is enhanced by about an order of magnitude, consistent with our simulation results presented above.

Zoom In Zoom Out Reset image size

Clear ripples can be identified at the front of the perpendicular shock after the interaction of upstream Alfvén waves with a shock. It means that the angle between the shock normal and the upstream magnetic field θ_Bn changes at the shock front. Therefore, the shock front has an irregular shape, and is a mixture of planar shocks with different shock angles θ_Bn. In this way, the dynamics of the reflected ions by the shock will be different from the case without injected Alfvén waves. How it will affect the mechanisms of ion acceleration at perpendicular shocks is our future topic.

We thank Garry Webb at the University of Alabama in Huntsville for valuable discussions. Q.M.L. was partly supported by the National Science Foundation of China (NSFC) under grants Nos 40725013, 40674093, 40874075, and Chinese Academy of Sciences (KJCX2-YW-N28).