ABSTRACT
For studies of tidal evolution, values of the key parameter Q, and its frequency dependence, are often derived from estimates of internal energy dissipation when a satellite, planet, or star is physically distorted. Such estimates come from geophysical or astrophysical modeling, from seismic data, from ad hoc assumptions, or from constraints based on current spins and orbits. In a standard procedure, Q values are used to determine the lag in the response to each Fourier component of the tidal potential. The separate components are then co-added. The basis for this procedure is the analogy of the damped, driven, harmonic oscillator. However, this lag-and-add procedure would not be justifiable even for such a simple system, except for a very specific dependence of Q on frequency. There is no reason to expect the lag-and-add procedure to be relevant for a complex system, because the relationship between dissipation rates and tidal lags is unknown. This widely applied type of model is a reasonable approximation only if the decomposed tidal potential involves a narrow range of frequencies, and thus may only be appropriate for analyses to low order in orbital eccentricity and inclination.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Tidal evolution of orbits and rotation has been modeled throughout the astrophysical literature by treating the tidal potential that acts on a body as the sum of Fourier components, each with its own frequency. The resulting deformation of the body is assumed to be the linear sum of responses to each separate forcing component. Each component of the response is characterized by parameters that describe the amplitude (Love numbers) and by a phase lag, which is assumed to result from energy dissipation in the material of the body.
The simplest case would be a satellite orbiting a primary in a circular, equatorial orbit. The alignment of the tidal potential at the primary tracks the direction of the satellite, but the potential is otherwise fixed in amplitude and figure. As the tidal potential rotates around relative to its body, the material of the primary periodically deforms. A standard picture of the response is shown in Figure 1. The amplitude of the distortion is assumed to be nearly identical to what it would be for synchronous periods. But the time lag in the response, due to dissipation, results in an angular displacement (ε/2 in Figure 1) of the distortion of the figure relative to the potential. The asymmetry introduced in this way results in torques that change both the satellite's orbit and the primary's spin.
Figure 1. Lag of the tidal response offsets the orientation of the elongation.
Download figure:
Standard image High-resolution imageIf the satellite's orbit is eccentric, the tidal potential varies in more complicated ways. The potential changes amplitude and direction, tracking the epicyclic motion of the satellite (Figure 2). It can be treated as a sum of second-order spherical harmonic components (Figure 3): a primary component that tracks the mean direction of the satellite, and two traveling components of different amplitudes (each proportional to the orbital eccentricity e) that circulate (relative to the satellite's direction) around the planet in opposite directions. A fourth periodic component (not shown in Figure 3) is an oscillation of the amplitude of the polar flattening of the planet's figure.
Figure 2. Tide (black bulges) on a planet (at left) is shown schematically at four points in the orbit of the tide-raising satellite, in a reference frame rotating with the satellite's mean motion.
Download figure:
Standard image High-resolution imageFigure 3. At right is the total tidal potential from Figure 2, at the four points in the satellite's orbit. The potential can be broken down into components: one locked to the average direction of the satellite, plus two components traveling clockwise and counterclockwise. The lag in the tidal response to each is represented by the offsets shown in gray.
Download figure:
Standard image High-resolution imageEach of these components drives the distortion of the material of the planet at a particular frequency. For example, the primary component drives the planet at a frequency of twice the difference between the spin rate and the orbital mean motion. (The factor of 2 accounts for the symmetrical double bulges of the tidal figure.) Moreover, the components described above represent only those up to first order in e. Taking into account higher orders in e would introduce an arbitrarily large number of harmonics with frequencies increasingly different from the primary one. Additional components are introduced by any orbital inclination as well.
Analytical treatments of tides over the past half century have usually adopted a "lag-and-add" approach (e.g., Kaula 1964). That is, they assume that the response of the planet to each of these multiple driving components is a separate distortion that lags in time (thus in angular orientation) relative to the driving potential. In other words, each component is assumed to behave similarly to the single-component case (Figure 1, with zero e, zero inclination). The actual figure at any instant is taken to be the sum of all these components.
Each component is generally assumed to have its own phase lag ε, which depends on the properties of the material. Recent critical reviews of the many various models, analyses, and assumptions in the history of this field have been presented by Ferraz-Mello et al. (2008) and by Efroimsky & Williams (2009). The former includes a high-order exposition of the harmonics of the tidal response, including an explicit display of the separate phase lags (without any assumptions about their frequency dependence).
In several influential studies, the simple assumption has been that ε is the same for all components, independent of frequency. This approach was adopted, for example, by MacDonald (1964) and by Goldreich & Soter (1966). A nagging problem with that assumption has been that the lag remains constant no matter how small the frequency is, but must drop discontinuously to zero at zero frequency. Moreover, the sign of the angular displacement can reverse discontinuously depending on the direction of the tidal rotation relative to the body.
An alternate approach is to assume that the phase lag is proportional to the frequency (e.g., Jeffreys 1961; Singer 1968; Mignard 1979, 1980; Hut 1981). This assumption is equivalent to assuming a constant time lag (not a constant phase lag) for all frequencies. (Note that Mignard and Hut did not Fourier-decompose the tidal potential, but accounted for dissipation by applying a time lag to the response, which is equivalent to the lag-and-add method with the phase lag proportional to frequency.) This frequency dependence avoids the discontinuity at zero frequency, but it introduces the potential problem that at very high frequencies a component's lag could be large relative to the period. An underlying rationale for this frequency dependence is that it was demonstrated by Darwin (1879) to follow from a specific and highly idealized model of a uniform, viscoelastic planet. Darwin's work also showed that dissipation also affects the amplitude of each component as well as the lag (Efroimsky & Williams 2009), whereas the usual lag-and-add procedure (whatever the lag assumptions) assumes that the effects on amplitude are negligibly small.
There have been numerous attempts to determine a relationship between ε and the frequency that is less arbitrary than any of the above assumptions. One type of approach takes advantage of the system's quality factor Q, which is defined, by analogy with the theory of harmonic oscillators as
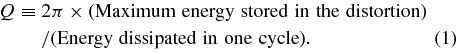
For a simple driven harmonic oscillator, tan ε = 1/Q, as reviewed in Section 2. This relationship opens the door to computing ε from geophysical models of how energy is stored and dissipated in a periodically distorted planet, satellite, or star. Depending on the type of body under investigation, the dissipation could involve viscoelastic behavior of solids, flow in liquid layers, turbulence in gases, or any other dynamic processes internal to an astronomical body. Then, after Q is evaluated, the relationship between Q and ε yields the lag for that driving period (e.g., Zahn 1977; Hut 1981; Segatz et al. 1988; Ogilvie & Lin 2004, 2007).
Another method for evaluating ε has been to consider seismic measurements on the Earth and Moon. The idea is that seismic waves are known to attenuate at various rates depending on frequency (Efroimsky & Lainey 2007). Thus, we have data that directly relate to the actual observed behavior of a planetary body, at least for rocky planets. This attenuation is used to compute Q from Equation (1). Efroimsky and Lainey quote seismic data suggesting Q ∝ (frequency)α, where α = 0.2–0.4.
All of these approaches have been motivated and implicitly justified by the analogy with a simple harmonic oscillator. However, even as models have become more complex and ambitious, the relevance and rigor of that underlying rationale have not been brought under scrutiny. Therefore, it is instructive to go back to basics and review the theory of the harmonic oscillator to consider whether it really provides a valid justification for the lag-and-add methodology. As I show below, many of the approaches that have been assumed to be applicable to modeling the behavior of complex planetary systems are not well justified even for a simple oscillator. This result calls into question the underlying assumptions and methods implicit in much tidal modeling.
2. HARMONIC OSCILLATOR
The lag-and-add model is based on the well understood idealized system built of a spring and damper. The spring is described by

where F is the force and x is the displacement; the damper is described by

where ν is the damping coefficient. If the damper and spring are arranged in parallel (a "Kelvin–Voight" system), so that their forces add and displacements are equal, the system would behave according to
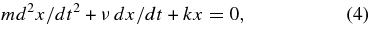
where the force of the system acts on a mass m.
If instead the spring and damper were in series (a "Maxwell" system), the equation takes the form
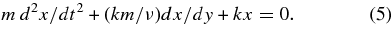
This series system is similar to a viscoelastic material (e.g., Silly Putty), which acts like an elastic solid when subjected to rapidly changing stress and like a viscous fluid under slow stress. Solid planetary materials are often assumed to behave as viscoelastic solids.
In either case, the governing Equation (4) or (5) is of the same linear form

where a periodic driving force has been added on the right-hand side. Here the left-hand side of the equation represents the character of the system, which allows us to compute the response to the input on the right-hand side. Note V is ν/m or km/ν for the Kelvin–Voight or Maxwell models, respectively; and ω2 = k/m in either case. The "natural frequency" of the system is ω.
The solution of Equation (6) is well known. Because the equation is linear, separate homogeneous (unforced) and forced solutions can be obtained, and the solution is their sum. The unforced solution is
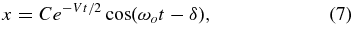
where
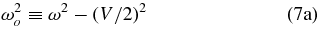
and C and δ are constants of integration determined by the initial condition. The dissipative V term in Equation (6) modifies the frequency of the unforced oscillation (Equation (7a)), and also damps it out on the timescale 2/V (Equation (7)).
The forced term in the solution is
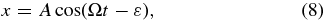
where the amplitude is
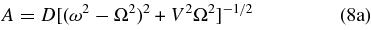
and the phase lag ε (relative to the driver on the right side of Equation (6)) is given by
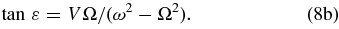
Note that tan ε depends directly on the damping V (Equation (8b)). Also, while the lag in phase is ε, the lag in time is given by ε/Ω.
If we assume tan ε ≪ 1, then tan ε ≈ ε, VΩ ≪ ω2 − Ω2, and
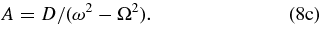
The denominator of Equation (8c) shows that the system resonates if the driving frequency Ω is near the natural frequency ω. Furthermore, if the system is driven at a rate much slower than the natural frequency (i.e., Ω ≪ ω), then ε = VΩ/ω. These results are similar to Darwin's (1879) model of a uniform, viscoelastic planet in a couple of ways: the phase lag ε is proportional to the driving frequency Ω; and the amplitude A is proportional to cos ε (as follows from Equations (8a) and (8b), and generalized by Alexander 1973).
This solution can be related to the dissipation rate in the system by evaluating Q, as defined in Equation (1). The energy loss is given by the dissipative force (from the second term in Equation (6)) times the distance traveled:
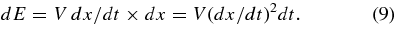
Then, using the solution (Equation (8)) to evaluate dx/dt in Equation (9), and integrating Equation (9) over one cycle (period = 2π/Ω) yields

The energy stored in the spring at any time is ω2x2/2, so
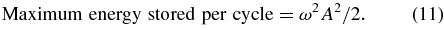
Then, Q (defined in Equation (1)) can be evaluated by dividing Equation (11) by Equation (10). Using A from Equation (8c) then yields
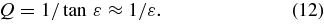
3. IMPLICATIONS FOR TIDAL EFFECTS
Real planets, satellites, and stars are much more complicated than the simple oscillator described above, but the standard lag-and-add approach implicitly assumes that characteristics of the behavior of the oscillator can be applied to all these systems. To be clear about the analogy, the left side of Equation (6) characterizes the system (analogous to the astronomical body), the right side represents the periodic distorting force (analogous to the tidal potential), and x is analogous to the response of the body. The tidal potential may involve the sum of many Fourier components acting over a wide range of frequencies, which for the analogous system above corresponds to multiple terms on the right side of Equation (6), where the solution would simply be the sum of corresponding terms in Equation (8) for every driving frequency Ω, plus the homogeneous solution (Equation (7)).
The lag-and-add model has traditionally been assumed, by implicit analogy with the harmonic oscillator, to be applicable to tides, i.e., that the planetary response can be calculated for each driving frequency and the results co-added. That assumption is a great leap of faith, but it is not unreasonable. However, nearly all tidal theories go a step further: it is generally assumed that the behavior of each of the components of the response has a lag specific to its driving frequency. It is supposed that the lag for each frequency can be determined by evaluating Q, either by theoretical models of dissipation, or based on seismic data. As discussed in the introduction, these estimates give a variety of estimates of values of Q and of its frequency dependence.
However, in the review of the harmonic oscillator above, Equation (8b) shows that the lag ε (and equivalently Q) has a very specific dependence on frequency determined by the intrinsic character of the damped oscillator. The harmonic oscillator system as defined above is not consistent with any other frequency dependence than Equation (8b).
Is it possible to modify the system in such a way that it remains linear (allowing the lag-and-add procedure) while giving a different frequency dependence for Q? Because Equation (8b) includes the coefficient V, one might try to model a particular frequency dependence for Q by invoking a frequency-dependent form for V. But that would require a system whose physical properties (left side of Equation (6)) depend on the sinusoidal driving frequency. It is not clear how a system with V = V(Ω) would respond to a nonsinusoidal driving function. Put another way, while one could rewrite Equation (6) with V as any function of Ω, if the right-hand side is the sum of sinusoidal drivers of different frequencies (each with its own Ω), the equation is no longer linear, or even mathematically meaningful. The basic premise of solving a linear equation, that you can solve for a separate solution for each driving frequency and then add up the solutions, would not be valid.
Thus, for this simple system (which is the implicit basis of the lag-and-add tidal models), there is no justification for allowing the frequency dependence of Q to be anything other than what is shown in Equation (8b). By analogy, if the lag-and-add method is to be applied to a system as complex as a planet, it probably could only work for a very particular frequency dependence of Q. For any other frequency dependence of Q, the assumption of linearity and additive superposition (i.e., the lag-and-add method) is unjustified. For the behavior of a real planet, the a priori probability that the physical properties of the planet yield exactly the required frequency-dependent Q is vanishing small.
Despite the difficulty described above, much of what has been inferred about tidal evolution of orbits and rotation is probably reasonable, but only to the extent that (a) the dissipation is small enough that it has a negligible effect on the amplitude (Equation (8a)) and (b) the harmonics that are included in the tidal potential have frequencies that are comparable. In that case, any issues arising from uncertainties in frequency dependence are probably buried in the greater uncertainty about the appropriate value of Q for any given frequency.
In general, the frequencies will not be very different from one another if an analysis is restricted to low-order terms in orbital eccentricity and inclination. So for such studies, the lag-and-add method is probably reasonably well justified.
However, for higher-order terms, the range of contributing frequencies becomes increasingly broad. Therefore, any analysis that attempts to derive tidal evolution to a high order in e or inclination, and uses the lag-and-add method, should be suspect.
4. RELEVANCE OF SEISMIC DATA
Distortions of a planet on various scales can oscillate, and waves can propagate over a wide and continuous range of frequencies. In contrast, the simple harmonic oscillator only has one natural frequency (ω introduced in Equation (6)). Thus, for a body where seismic attenuation is measured, it is possible to determine Q over a range of frequencies. Of course, as discussed in the previous section, even with this information, it is questionable whether the lag-and-add method of solution is valid unless only a narrow range of driving frequencies is considered.
Even if the lag-and-add method is reasonable, the relevance of the seismic Q is unclear. The seismic Q and the tidal Q are both defined according to Equation (1). However, for the reasons described below, it is not clear how the frequency dependence of Q as determined from seismic studies is related to the frequency dependence for the tidal Q. The seismic Q is determined from the damping of the natural oscillations (e.g., Karato 2008), while the tidal Q represents the energy loss due to forced oscillations. In order to see how different they can be, even in a simple system, again consider the harmonic oscillator of Equation (6). The seismic attenuation that gives Q (still defined by Equation (1)) is analogous to the damping in the unforced solution (Equation (7)):
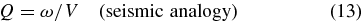
as noted also by Efroimsky & Lainey (2007). In contrast, for the driven solution (analogous to the tidal case), Equations (8b) and (12) yield

In tidal theory discussions of the frequency dependence of Q are concerned with the driving frequency (Ω); in seismic studies, Q is determined as a function of the frequencies of free oscillation (ω). Unfortunately, this distinction is rarely made. Even in the otherwise very insightful discussion by Efroimsky & Lainey (2007), in which they also used a simple damped harmonic oscillator to elucidate a more detailed analysis, this point is muddied by using the same symbol for both the free seismic frequency and the forced tidal frequency. Examination of Equations (13) and (14) shows that the values of Q and their frequency dependence as found in these two different ways would only be the same if Ω ≫ ω, in which case Equation (14) reduces to

Thus, there is probably no reason to assume a priori that, in a more complex planetary or stellar body, values of Q measured from the damping of seismic oscillations as a function of frequency ω would be the same as Q in tidal dissipation as a function of the forcing frequency Ω. The seismic values would only be relevant if (a) they are measured at frequencies comparable to the tidal driving frequencies and (b) the tidal frequency is high relative to the natural frequencies that correspond to the tidal distortion. These conditions would only be met in rare special cases if at all.
5. CONCLUSION
Stars, planets, and satellites are complicated mechanical systems. Their responses to tidal potentials that distort their shapes have important effects on their long-term physical and dynamical evolution. Analytic approaches to the problem have traditionally used the lag-and-add method, which is loosely based on the analogy of the driven harmonic oscillator, as described above. This approach is probably reasonable as long as all the frequencies of the varying tidal potential are comparable, as is the case for analyses that are restricted to low order in orbital eccentricities and inclinations.
Higher-order analyses, which introduce a wider range of frequencies, may not be so reliable if the lag-and-add procedure is applied. Introduction of frequency-dependent functions for Q into the standard lag-and-add method has no justification, because the analogous driven oscillator (which provides the supporting rationale for the lag-and-add procedure) only has a linear solution if Q has a very specific frequency dependence. Any other frequency dependence would make the system nonlinear. In general, Q values and frequency dependence determined by theory or seismic data probably do not have the usually assumed relationship to tidal lag.
I thank Rory Barnes and Brian Jackson for inspiring conversations, and Stanton Peale, Sylvio Ferraz-Mello, and Michael Efroimsky for comments on the manuscript. This research is supported by NASA's Planetary Geology and Geophysics program.





