ABSTRACT
The hunt for complex organic molecules (COMs) is a major concern for understanding the possible role of interstellar chemistry in the synthesis of the molecules that ultimately may be at the origin of life. A comprehensive screening of the 14 species effectively observed under 32 different isomeric forms in the interstellar medium has been done by means of high-level quantum chemical simulations. Confrontation between calculations and observations shows that when several isomers of the same generic formula are identified, it is always the most stable one that is the most abundant. Moreover, the abundance ratio of the most stable isomer to the other isomers is directly related to their energy difference. What can be seen as a minimum energy principle is verified in molecular clouds, hot cores/corinos, photodissociation regions, and asymptotic giant branch stars. The few exceptions encountered could be rationalized either by the existence of different routes of formation with no intermediate in common and/or specific depletion on the grains of one isomer with respect to the others.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
The fact that organic chemistry started in space can be considered a new challenge for the scientific community. Nowadays several N and O bearing complex organic molecules, called COMs in the literature, have been discovered in space, in different regions. Among the extrasolar objects, the Galactic center molecular clouds (Hollis et al. 2006), hot cores (Ikeda et al. 2001), and hot corinos (Bottinelli et al. 2007) are particularly rich in COMs. The same and even more complex COMs have been observed in comets (Sandford et al. 2006) and meteorites where amino acids have also been detected (Pizzarello et al. 2001), making the link between the interstellar medium (ISM), star formation, and planetary systems more than a philosophical conjecture. Despite its importance, not much is known about the way COMs are formed and destroyed. Three different chemistries have been proposed: gas phase ion–molecule and neutral–neutral reactions, solid–gas processes on the grain surfaces, and excited state interactions with UV/X-rays, electrons, or heavier particles. At the moment, it is totally unclear which is important and when. In this context, the isomers of COMs could be a very precious tool because they may pinpoint formation routes (Hollis et al. 2006).
Among the ∼150 species identified up today in the interstellar and circumstellar media, more than a dozen of systems have been observed under the form of two or more isomers. The main goal of this study is to look for the relation between the thermodynamic stability and the abundance of COMs isomers. To this purpose, we report a coherent and systematic study of the relative stability of all COMs with more than one isomer detected in the ISM.
2. COMPUTATIONAL METHODS
Density functional theory (DFT) was employed in a first approach using the hybrid B3LYP formalism coupled with two levels of basis sets: standard split-valence polarized 6-311G(d, p) and correlation consistent cc-pVQZ. Each structure, fully optimized, was verified to be a stationary point by vibrational analysis. A final estimate of the energy differences was calculated at the highly correlated CCSD(T)/cc-pVQZ level of theory using the geometry and ZPE obtained at the B3LYP level with the same basis set. For each molecule, several conformers were studied but only the most stable one is reported. We have verified that including entropic terms to determine Gibbs free energies of formation at the temperature of the various sources considered here has a marginal impact on the values of the energy differences.
All the calculations were performed using the GAUSSIAN03 package.
3. DISCUSSION
Table 1 summarizes the observed abundances ratios of all molecules with more than one isomer detected in space, to our best knowledge. Since these values may depend on the source where the isomers were detected, we very roughly divided them into four classes, corresponding to sources with different environment conditions (temperature, density, UV illumination...): molecular clouds (MC), hot cores or hot corinos (HC), photodissociation regions (PDR), and asymptotic giant branch stars (AGB).
Table 1. Abundance Ratios of the Observed Isomers
| Most Stable Isomer (1) | Other Isomers (2) | Ratio (1)/(2) | Object | Reference |
|---|---|---|---|---|
| HCO+ | HOC+ | 350-6000 | MC | 1 |
| 150-1800 | HC | 2 | ||
| 50-7000 | PDR | 3,4 | ||
| HCN | HNC | 0.6-3 | MC | 5,6 |
| 5-80 | HC | 7,8 | ||
| 0.5-3000 | PDR | 3 | ||
| 10-200 | AGB | 9,10 | ||
| cyc-C3H | l-C3H* | 5-15 | MC | 11,12 |
| 2 | PDR | 13 | ||
| cyc-C3H2 | l-C3H2 | 10-70 | MC | 14 |
| 50-150 | HC | 14 | ||
| 30 | PDR | 13 | ||
| 30 | AGB | 14 | ||
| HNCO | HCNO | 40-90 | MC | 15 |
| > 1000 | HC | 15 | ||
| CH3CN | CH3NC | 50 | MC | 5,16,17 |
| > 50 | HC | 17 | ||
| CH2CNH | ∼100 | HC | 18 | |
| CH3CHO | cyc-C2H4O | 2-10 | HC | 19,20 |
| CH2CHOH | 2-10 | HC | 21 | |
| CH3CH2OH | CH3OCH*3 | 0.3-3 | HC | 20,22,23 |
| HC3N | HC2NC | 20-60 | MC | 24 |
| 20-200 | AGB | 25,26 | ||
| HNC3 | 160-450 | MC | 27 | |
| 1000 | AGB | 25 | ||
| HC2CHO | cyc-H2C3O | 5 | MC | 28,29 |
| CH3COOH | HCOOCH*3 | 0.01-0.1 | HC | 30,31, |
| 32,33 | ||||
| CH2OHCHO | ∼0.05 | MC | 34 | |
| ∼0.05 | HC | 34,35 | ||
| CH3-CC-CN | CH2=C=CHCN | 0.25 | MC | 18 |
| MgNC | MgCN | 20 | AGB | 36,37 |
| SiCN | SiNC | 1 | AGB | 38,39 |
Notes. The first and second columns report the most stable and other isomers of the same generic formula, the third column the abundance ratio between them, the fourth column the astrophysical object where the ratio has been observed, and the fifth column the references to the observations. References. (1) Ziurys & Apponi 1995; (2) Apponi & Ziurys 1997; (3) Fuente et al. 2003; (4) Fuente et al. 2005; (5) Irvine & Schloerb 1984; (6) Tennekes et al. 2006; (7) Goldsmith et al. 1986; (8) Schilke et al. 1992; (9) Guelin et al. 1986; (10) Pardo et al. 2005; (11) Turner 2000; (12) Fossé et al. 2001; (13) Teyssier et al. 2004; (14) Cernicharo et al. 1999; (15) Marcelino et al. 2009; (16) Cernicharo et al. 1988; (17) Remijan et al. 2005; (18) Lovas et al. 2006; (19) Nummelin et al. 1998b; (20) Ikeda et al. 2001; (21) Turner & Apponi 2001; (22) Nummelin et al. 1998a; (23) White et al. 2003; (24) Kawaguchi et al. 1992a; (25) Gensheimer 1997; (26) Pardo et al. 2007; (27) Kawaguchi et al. 1992b; (28) Hollis et al. 2006; (29) Turner 1991; (30) Mehringer et al. 1997; (31) Remijan et al. 2002; (32) Remijan et al. 2003; (33) Cazaux et al. 2003; (34) Hollis et al. 2001; (35) Hollis et al. 2004; (36) Guelin et al. 1986; (37) Kawaguchi et al. 1993; (38) Guélin et al. 2000; (39) Guélin et al. 2004.
Download table as: ASCIITypeset image
The dipole moments and relative stabilities of the different isomers of the same generic formula were computed according to the methods described in the previous section, and were found to be very little affected. Only the CCSD(T)/cc-pVQZ values, considered the best estimates, are reported in Table 2 and used in the discussion. Dipole moments (B3LYP/cc-pVQZ) are also given since they may be critical for understanding the relative abundances observed.
Table 2. Computed Relative Stability (kcal mol−1) and Dipole Moments (Debye) of Isomers
| Generic Formula | Most Stable Isomer | μ Isomers | Other | μ | ΔE |
|---|---|---|---|---|---|
| CHO+ | HCO+ | 3.7 | HOC+ | 2.6 | 37.96 |
| CHN | HCN | 3.0 | HNC | 3.1 | 14.47 |
| C3H | cyc-C3H | 2.3 | C3H | 3.6 | 1.25 |
| C3H2 | cyc-C3H2 | 3.5 | l-C3H2 | 4.4 | 13.75 |
| CHNO | HNCO | 2.1 | HCNO | 3.2 | 69.0 |
| C2H3N | CH3CN | 4.0 | CH3NC | 3.9 | 24.32 |
| CH2CNH | 1.4 | 27.15 | |||
| C2H4O | CH3CHO | 2.8 | CH2CHOH | 0.9 | 10.31 |
| cyc-C2H4O | 1.9 | 27.78 | |||
| C2H6O | CH3CH2OH | 1.6 | CH3OCH3 | 1.2 | 12.01 |
| C3HN | HC3N | 3.9 | HC2NC | 2.9 | 26.84 |
| HNC3 | 5.5 | 51.42 | |||
| C3H2O | HC2CHO | 2.9 | cyc-H2C3O | 4.2 | 6.79 |
| C2H4O2 | CH3COOH | 1.7 | HCOOCH3 | 1.9 | 17.14 |
| CH2OHCHO | 2.4 | 27.24 | |||
| C4H3N | CH3-CC-CN | 5.3 | CH2=C=CHCN | 4.4 | 3.76 |
| CNMg | MgNC | 5.3 | MgCN | 5.4 | 1.42 |
| CNSi | SiCN | 3.1 | SiNC | 2.7 | 1.54 |
Notes. The first column reports the generic formula of the molecules, ordered in increasing molecular weight. The next two columns report the most stable isomer with its dipole moment; fourth and fifth columns report the less abundant isomer(s) with the relevant dipole moment; last column reports the computed relative stability with respect to the most stable.
Download table as: ASCIITypeset image
Note that a number of the molecules listed in Table 2 have already been studied in the past, using various levels of theory. These calculations, although generally performed with the most relevant methods at the time when the molecules were discovered, led in the end to a rather inhomogeneous body of data. Here, one considers all molecules on an equal footing that is the best that can reasonably be used for such study and the extensive surveys to come. In all cases where previous studies have been published, our results confirm the general trends and characteristics obtained.
3.1. The Minimum Energy Principle
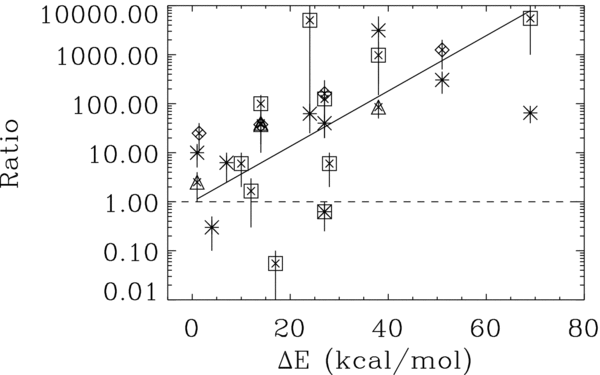
Figure 1 shows, for each type of object, the measured abundance ratios (reported in Table 1) as a function of the difference in energy of each isomer, with respect to the most stable one (namely that with the lowest energy). Despite the relative large uncertainty in the abundance ratios,3 this figure shows two striking properties: (1) the most stable isomer is the most abundant; and (2) there is a relationship between the ratio of the most stable isomer abundance with respect to other isomers of the same generic formula and the difference in energy of the two isomers: the larger the energy difference between the two isomers, the larger the abundance ratio between the most stable and less stable isomer.
Figure 1. Ratio of the measured abundance of the most stable isomer with respect to other isomers of the same generic formula vs. the difference in energy between the two isomers, as computed in this work (see Table 1). The different symbols refer to different astronomical sources: asterisks to molecular clouds, squares to hot cores/corinos, triangles to photodissociation regions, diamonds to AGB stars. The bars show the interval of the measured values for each astronomical source. The line is a best fit obtained excluding the points that lie below the ratio value 1 (see the text).
Download figure:
Standard image High-resolution imageThese two properties form what we call here the minimum energy principle,4 hereafter referred to as the MEP.
In practice, Figure 1 says that what matters mostly in the relative abundance of the isomers of the same generic formula is the relative energy, with just two exceptions in the sample of the 32 detected molecules (cf. the next section).
It is often considered that the different isomers of the same generic formula are the result of different formation and destruction routes and behave like strangers. Against this statement, the MEP suggests that the chemical formation and destruction routes only play secondary roles.
We see at least three possible reasons that would explain the data of Figure 1.
- 1.The isomers of same generic formula reported in Figure 1 have all a common intermediate in their formation and destruction route and the branching ratio from this intermediate/transition state determines the relative abundances of the products.
- 2.There is an equilibration process after reaching the generic formula: internal isomerization with a low activation barrier, assisted isomerization, or catalytic isomerization at the grain/ice surfaces. Such a process would require local thermodynamic equilibrium (LTE) at the time of equilibration;
- 3.There is a selective depletion of one isomer compared to the other.
Most probably, it is a conjunction of these reasons that takes place, with different relative importance according the type of object.
To illustrate the point, we will consider in detail the three molecules which "best" satisfy the MEP (being those with the largest energy differences in Table 2): HOC+, HNC3, and HCNO.
HOC+. There is little doubt that HCO+ is a gas phase chemistry product: in cold molecular clouds, it is mainly formed by the reaction of CO with H+3, while in PDRs it is the product of reactions with C+ and CO+. Theoretical calculations (Herbst & Woon 1996) and laboratory experiments (Smith et al. 2002) have studied the isomerization of HOC+ into HCO+ by reactions with H2 and established that it has essentially no energy barrier. The fact that the denser and warmer PDRs also have a lower HCO+/HOC+ ratio supports the idea that isomerization of the rarer isomer HOC+ mostly governs the HCO+/HOC+ ratio in astronomical sources. It is a case (2) example where mediation by H2 lowers an activation barrier from ∼40 kcal mol−1 to a mere ∼1 kcal mol−1. Such a equilibration process could be efficient for any proton transfer.
HNC3. It has been so far detected in two sources only, TMC-1 (Kawaguchi et al. 1992b) and IRC10216 (Gensheimer 1997). There is no consensus on the dominant formation routes of HC3N and HNC3: either they may both be formed by the electron recombination of the ion HC3NH+, or HC3N may be formed by the reaction C2H2 + CN that does not form HNC3 (Herbst & Leung 1990). The observed ratio suggests that any difference in the formation or destruction of these two molecules is wiped off by isomerization. In that case, one has also to look for another mechanism, the two extremities of the CCCN chain being too far apart for an easy hydrogen transfer. The most likely mediator is atomic hydrogen via the hydrogen exchange reaction: HNCCC + H → H + NCCCH. It is the equivalent of HNC/NCH addition–elimination reaction that has been shown to divide the intramolecular isomerization barrier by a factor of 8 (Talbi et al. 1996). In the same way, mediation by H2O via a cyclic hydrogen transfer on the ice (Gardebien & Sevin 2003) could be effective. It is another case (2) example, pertinent to the gas phase and surface chemistry as well.
HCNO. The isomer in Table 2 with the largest energy difference with respect to the most stable is fulminic acid (HCNO), recently discovered in a few molecular clouds by Marcelino et al. (2009). As remarked by these authors, there is not a mother molecule common to HNCO and HCNO and, in principle, they may be formed either in the gas phase or on the grain surfaces. It is certainly worth noticing that in molecular clouds the HNCO/HCNO ratio is smaller than in the hot cores (where only an upper limit exists). This is also often the case for the other isomers of Table 2, and is consistent with the idea that isomerization takes place and that it is more efficient in warmer and denser environments. More observations are necessary to firmly draw a conclusion, but the available data seem to suggest that the relative abundance of HNCO and HCNO is rather determined by their energy difference than the history of their formation, a point of view substantiated by the shape of the potential energy surface (Mebel et al. 1996).
In summary, even if the three pairs of isomers with the largest energy difference possess different formation and destruction routes, the fact that, at the end, the three pairs with the largest energy difference have also the largest abundance ratios is in favor of the idea that isomerization (at some time in the history of these species) is the most important process in determining their relative abundances.
3.2. Exceptions to the Minimum Energy Principle
The plot of Figure 1 shows two exceptions to the MEP where the most stable isomer is not the most abundant.
The first molecule is the CH2=C=CHCN, which has been measured to be more abundant than the most stable isomer of the same generic formula, the CH3–CC–CN. The observations have been obtained toward the TMC-1 molecular cloud, where Lovas et al. (2006) found that CH2=C=CHCN is about 4.5 times more abundant than CH3–CC–CN. Note, however, that the abundance of CH3–CC–CN is based on one transition only. These authors privilege the thesis that the larger abundance of CH2=C=CHCN with respect to CH3–CC–CN is due to the formation route of these molecules. Considering the counter-examples offered by Figure 1, this is not a satisfying enough explanation to us. Something else must be different in these molecules with respect to the other molecules which follow the MEP, should this anomaly be confirmed by other observations.
The other two exceptions to the MEP are both isomers of the generic formula C2H4O2 and refer to the case of acetic acid (CH3COOH), methyl formate (HCOOCH3), and glycoaldehyde (CH2OHCHO). Based on our computations, acetic acid is the most stable isomer. However, in all astronomical sources where it was searched for, acetic acid is at least 10 times less abundant than methyl formate and has about the same abundance as glycoaldehyde. While the latter measurement is subject to a relatively large uncertainty because it refers to one source only and with a relatively large error bar, the fact that methyl formate is at least 10 times more abundant than acetic acid is a robust observational fact, observed in several hot cores and corinos. In fact, the anomaly of these two isomer pairs seems to be the relatively large abundance of methyl formate: if it were 10 to 50 times lower than that observed both acetic acid and glycoaldehyde would fall in the curve of Figure 1 and would respect the MEP. What could then make methyl formate different? Horn et al. (2004) examined the formation routes for methyl formate and could not find any efficient way to form it in the gas phase. They concluded that it is likely formed on the grain surfaces. In this case, we propose that this exception could be the result of a stronger adsorption of CH3COOH on the grains due to the presence of an acid hydrogen in the COOH group that has no equivalent in methyl formate (M. Lattelais et al. 2009, in preparation). If one considers that these species are coming from independent chemical routes, another possible explanation would be the presence of a high energetical barrier making the isomerization process itself quite impossible. In this case indeed, such a process requires the concerted breaking of two chemical bonds that is very energy demanding and most unlikely.
4. CONCLUSION
The present study of the series of molecules observed in space under two or more isomeric forms shows a strong relationship between the observed abundances and the energy differences relative to the most stable isomer. What can be seen as a minimum energy principle seems to govern the abundance ratio between isomers, pointing to local thermal equilibrium at a time or another along the chemical history of these species. Our finding suggests that the LTE hypothesis could be more general than originally thought. It is premature at this stage to draw firm conclusions, but if the minimum energy principle is confirmed on a larger number of isomers and objects, it would have a large impact on theories of interstellar chemistry, so far uniquely based on kinetics effects. It would indicate that, someway/somehow along the path, LTE effects have to be taken into account in the interstellar space molecule formation. The existence of the MEP explains why the first observed isomers are also the most abundant since they are the most stable. The few exceptions to the MEP could be explained either by completely disconnected formation routes associated with high energy barriers impeding the interconversion processes, or by a phenomenon of differential adsorption on the grains. Calculations in progress on a series of larger COMs (amides, nitriles, alcohols...) to be reported show that the molecules observed are effectively the most stable ones in their respective families.
This work was supported by CNRS national programs PCMI (Physics and Chemistry of the Interstellar Medium) and OPV (Origins of Planets and Life). Part of the calculations were performed at the CINES supercomputing center.
Footnotes
- 3
In fact, the published abundances or column densities are not always corrected for the line opacities, or it is not always certain that the two isomers are cospatially located. In general, the ratios result from beam-averaged measurements, so that in this plot we assumed at least a factor 2 of uncertainty in all measures reported in Table 1.
- 4
We use here the world "principle," according to the definition given by the Dictionnaire de l'Académie Française/ARTFL Project, The University of Chicago (2001): In science, principle refers to laws which certain observations have first shown to be probable and to which the most extensive generality has then been given.