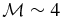ABSTRACT
We report the study of a pulsar wind nebula (PWN) in the middle-aged supernova remnant (SNR) MSH 15−56. High-resolution X-ray imaging observations using XMM-Newton and Chandra provided clear images of its comet-like structure, as seen in other PWNe moving rapidly through interstellar mediums. At the PWN apex, Chandra detected a point source emitting a power-law spectrum with a photon index of Γ = 1.3. The photon index of the PWN steepens from 1.7 to 2.5 along the flow line from the apex toward the tail, implying that the PWN is powered by the point source. The opening angle of the tail implies a pulsar velocity of vPSR = 1900 km s−1. We also discovered a thin X-ray filament at the edge of the SNR and just near the PWN. Assuming that the SNR is in the Sedov phase, the shell is expanding at 860 km s−1, which is consistent with the existence of the non-thermal filament. Based on the physical relationship, the PWN will run through the blast wave in the near future.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Currently, young rotation-powered pulsars are believed to have pulsar wind nebulae (PWNe) made from relativistic electron–positron plasma, as seen in the Crab Nebula (Weisskopf et al. 2000a; Hester et al. 2002), whereas in the case of a pulsar that is moving at supersonic velocity with respect to its surroundings, the pulsar wind generates a bow shock and forms comet-like structures consisting of a coma and a diffuse tail (Bucciantini 2002; van der Swaluw et al. 2003). At birth, most pulsars are harshly kicked by supernova (SN) explosions and move at an average velocity of a few hundred km s−1 (Frail et al. 1994). Therefore, those bow shock PWNe may represent the majority of such objects. The lifetime of PWNe appears to be a few tens of kyr. Adopting an SN rate of one SN per century in our galaxy, we can find no more than ∼100 active PWNe. To investigate the nature of rotating pulsars and their pulsar wind, every single bow shock PWN may be a crucial sample.
MSH 15−56 (G326.3−1.8 or Kes 25) is a composite-type supernova remnant (SNR). In the radio, the SNR shows a circular shell with a diameter of ∼36', whereas in X-rays, the SNR shows thermal emissions that originated in the hot plasma. For this SNR system, the standard Sedov analysis yields a dynamic age of τ ≃ 15 kyr and an ambient interstellar medium (ISM) density of n0 ≃ 0.1 cm−3 with an assumed distance of 4.1 kpc (Kassim et al. 1993; Dickel et al. 2000). The distance to the SNR remains unclear but a past H i observation derived a lower limit of 3.1 kpc (Goss et al. 1972) and most estimates range between 3.7 and 5.0 kpc. In this study, we adopt a distance of 4.1 kpc based on an Hα radial velocity measurement (Rosado et al. 1996).
At the southwest SNR rim, Plucinsky (1998) discovered a compact hard X-ray nebula. Although the object shows no pulse emissions, this is currently believed to be an X-ray synchrotron nebula around an undetected pulsar. The position offset of the PWN with respect to the center of the SNR is about 10', implying that the running velocity of the unknown pulsar driving the PWN is supersonic. Therefore, we expect to find a bow shock structure.
Past radio observations revealed a plerion-like feature near the center of the SNR (Clark et al. 1975, Milne et al. 1979, and references therein). The spectral index was α ≃ 0.04(S∝ν+α), which is obviously flatter than that of an SNR, α ≃ −0.4, measured at the shell. Moreover, the radio emission from the feature is significantly polarized as is typical for plerions (Milne et al. 1979). Although these spectral and morphological characteristics are reminiscent of a PWN, the location is completely distinct from the X-ray PWN. The significant offset between the radio plerion and the hard X-ray nebula has been one of the most intriguing issues for MSH 15−56. For this issue, Dickel et al. (2000) proposed a model: the SN explosion left a rapidly moving magnetar, which quickly lost its rotational energy in the form of relativistic particles that are still radiating in the radio near the birthplace of the magnetar.
To verify this hypothesis and to clarify the relationship between the radio plerion and the hard X-ray nebula, we performed imaging spectroscopy of the hard X-ray nebula utilizing modern high-resolution X-ray telescopes such as the XMM-Newton and the Chandra. In Section 2, we present a data analysis and the results from utilizing archive data of MSH 15−56 taken with XMM-Newton and Chandra. In Section 3, we discuss the structure and energetics of the PWN in detail.
2. OBSERVATIONS AND RESULTS
2.1. Observations
The southwest vicinity of MSH 15−56 was observed with XMM-Newton on 2004 August 11 (Observation ID: 0204270101). The aim point of the telescope was  , δ = −56°18'12
, δ = −56°18'12 0 (J2000.0), about 10' southwest of the center of the SNR. EPIC-MOS1/2 and PN operated in the prime full window mode with the medium filter. The data mode was set to "imaging."
0 (J2000.0), about 10' southwest of the center of the SNR. EPIC-MOS1/2 and PN operated in the prime full window mode with the medium filter. The data mode was set to "imaging."
Although the duration of the whole observation was 57.6 ks, half of the total exposure time was seriously damaged by background flares. Therefore, we created a Good Time Interval (GTI) file that can be used to create a filtered event file that only accepts good times where the background was low. To distinguish usable exposures from noisy time slots, we defined selection criteria based on the event rate. For this purpose, we made histograms of the event rate for 100 s intervals in the 10–12 keV energy band and fitted the histogram with a function consisting of a Gaussian and a power-law function. While the background flares show high variability, the good times are dominated by the steady cosmic X-ray background (CXB) event and correspond to the time intervals in the Gaussian regime on the histogram.
The best-fit parameters of the Gaussian function were μ = 0.075 ± 0.03 and σ = 0.03 ± 0.01 counts s−1, respectively, for both MOS1 and MOS2, which corresponds to the X-ray events from the target object and CXB. We also obtained the best-fit Gaussian function for PN: μ = 0.483 ± 0.009 and σ = 0.076 ± 0.009 counts s−1.
Consequently, we defined the upper threshold of the event rate as 2.706σ, which is equivalent to 0.15 and 0.69 counts s−1 for MOS and PN, respectively. The data sets were then filtered with the GTI file based on the criteria defined above using Science Analysis System (SAS) version 10.0. Finally, we obtained a usable data set with a 28.5 ks exposure.
The field of MSH 15−56 was also observed with the Chandra X-Ray Observatory (Observation ID: 1965) on 2001 August 18 using the back-illuminated CCD S3 of the ACIS (Burke et al. 1997). The detector was operated in the VFAINT, timed-exposure mode. We therefore applied a standard data reduction process to generate a level 2 event file with VFAINT-mode background cleaning using CIAO version 4.1 with CALDB version 4.1.3. In the process, we disabled pixel randomization to resolve fine structures just around the pulsar. The resulting usable exposure time was 56.1 ks.
2.2. X-Ray Images
2.2.1. Large-scale Structures (XMM)
To perform a morphological analysis and spatially resolved spectroscopy, we combined X-ray images of EPIC MOS and PN utilizing "Image_script," which is an analyzing script of SAS. The resulting X-ray images of the southwest rim of MSH 15−56 in four energy bands (0.2–1.2, 1.2–2.0, 2.0–10.0, and 0.2–10.0 keV) are shown in Figure 1. To clarify the physical relationship between the SNR and PWN, Figure 2 compares the X-ray and radio structures in MSH 15−56.
Figure 1. Exposure-corrected X-ray images of the SW edge of MSH 15−56 taken with EPIC MOS/PN aboard XMM-Newton. The spatial bin size is set at 2 0 and the binned images were smoothed with a kernel size of 5
0 and the binned images were smoothed with a kernel size of 5 0 in FWHM. Images correspond to energy bands of 0.2–1.2, 1.2–2.0, 2.0–10.0, and 0.2–10.0 keV, respectively. The contours show the surface brightness of the SNR at a 22 cm radio wave taken with ATCA. The circled regions labeled "A," "B," and "BG" are used in the spectroscopy of the SNR component described in Section 3.
0 in FWHM. Images correspond to energy bands of 0.2–1.2, 1.2–2.0, 2.0–10.0, and 0.2–10.0 keV, respectively. The contours show the surface brightness of the SNR at a 22 cm radio wave taken with ATCA. The circled regions labeled "A," "B," and "BG" are used in the spectroscopy of the SNR component described in Section 3.
Download figure:
Standard image High-resolution imageFigure 2. Comparison of radio and X-ray images of MSH 15−56. The colors correspond to 0.2–1.4 keV (red), 2.0–10.0 keV (blue), and 22 cm radio (green). The contours show the structure of the hard X-ray component. The circle with a radius of 16' centered on the cross mark is superimposed to indicate the outer boundary of the radio SNR.
Download figure:
Standard image High-resolution imageIn the 0.2–1.2 keV energy band, only a diffuse structure was observed. The soft component seems to fill the inside of the SNR and shows a sharp edge at its southwest rim, while the harder energy bands revealed a compact nebula with a coma and a diffuse tail. Those morphological features distinguish the object from other background point sources. The hard X-ray nebula extends about 2' in the direction of the SNR center (see Figure 2).
2.2.2. Fine Structures (Chandra)
Chandra reveals more fine structures. Figure 3 shows a close-up view of the PWN in the 0.4–8.0 keV energy band with a binning size of 4 × 4 pixels (∼2'' × 2''). Although the PWN apex appears to be a point source, we tried to search for the extended component correlating with the wind termination shock, as seen in the Mouse nebula (Gaensler et al. 2004). To constrain the size of the emitting region, we analyzed the Chandra image using Sherpa in CIAO (Freeman et al. 2001). Since the size of the brightest part of the PWN appears to be comparable with the point-spread function (PSF) of the HRMA, we evaluated the intrinsic size of the nebula. For this purpose, we made a PSF of the HRMA as a convolution kernel with the ray trace simulator ChaRT (Carter et al. 2003) for the target position and the observed spectrum.
Figure 3. Close-up view of the pulsar wind nebula in the 0.4–8.0 keV energy band observed by Chandra. To enhance image quality, we employed a binning size of 4 × 4 pixels that corresponds to 1 968 × 1
968 × 1 968.
968.
Download figure:
Standard image High-resolution imageThe close-up X-ray view of the apex compared with the HRMA's PSF is shown in Figure 4, and Table 1 shows the results of model fitting with a two-dimensional Gaussian function indicating that the angular size of the coma exceeds the PSF to some extent. The angular size of the coma is 1 7 ± 0
7 ± 0 4 in FWHM. The model fitting also constrains the precise coordinate of the point source,
4 in FWHM. The model fitting also constrains the precise coordinate of the point source,

though that still contains a systematic error of about ±0 6 (with a 90% confidence level).4
6 (with a 90% confidence level).4
Figure 4. Two-dimensional model fitting with an HRMA's PSF as a convolution kernel. (a) The observed X-ray image with a bin size of 0 246 × 0
246 × 0 246. (b) The best-fit model function (two-dimensional Gaussian) convolved with the HRMA's PSF. (c) The residual of model fitting. (d) The point-spread function of HRMA generated with the Chandra Ray Tracer (ChaRT). The resulting parameters are summarized in Table 1.
246. (b) The best-fit model function (two-dimensional Gaussian) convolved with the HRMA's PSF. (c) The residual of model fitting. (d) The point-spread function of HRMA generated with the Chandra Ray Tracer (ChaRT). The resulting parameters are summarized in Table 1.
Download figure:
Standard image High-resolution imageTable 1. Results of Two-dimensional Model Fitting of the Chandra Image
| Parameter | Best Fit | Lower Bound | Upper Bound |
|---|---|---|---|
| Gaussian component | |||
| X-position (J2000) | 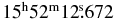 |
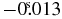 |
 |
| Y-position (J2000) | −56°18'58 26 26 |
−0 18 18 |
+0 19 19 |
| FWHM (arcsec) | 1 71 71 |
−0 40 40 |
+0 42 42 |
| Amplitude (counts) | 12.5 | −4.5 | +8.9 |
| Constant component | |||
| Amplitude (counts) | 0.068 | −0.002 | +0.002 |
Note. Errors are within a 90% confidence level.
Download table as: ASCIITypeset image
The tail was resolved into a wedge shape that is brightening at the edges. The west side of the wedge is clear and shows a mildly curved line extending ∼1' from the point source, while the opposite side is relatively unclear due to the superimposed arc-like structure on the south edge of the SNR (see below). The apparent half opening angle of the wedge is θapp ∼ 25°.
Near the PWN apex, an arc-like faint filament extends eastward, labeled "ARC" in Figure 3. This feature is also observed with XMM-Newton but only in the hard X-ray band. Figure 5 describes the surface brightness distribution along the line normal to the arc. While the soft X-ray component appears to fill the SNR as seen in Figure 2, the hard X-ray component was only detected at the edge of the SNR. The hard X-ray filament has a width of about 20'', which may be due to the three-dimensional geometry projection of the SNR. Nevertheless, the sharply rising outer edge implies the existence of a very thin (∼10'') structure that may be associated with a non-thermal X-ray filament as seen in young SNRs (Bamba et al. 2003).
Figure 5. One-dimensional projection of the surface brightness of the rectangular region marked in Figure 2. The upper and lower data series represent the 0.4–8.0 and 2.0–8.0 keV energy bands, respectively. The vertical error bars indicate the statistical errors.
Download figure:
Standard image High-resolution image2.3. Spectroscopy
2.3.1. SNR Component
Because the PWN appears in the SNR on the celestial sphere, we first evaluated the SNR component before investigating the PWN in detail. For this purpose, we selected regions "A" (a = 3 2, b = 1
2, b = 1 2) and "B" (r = 3') denoted in Figure 2. Region A is the brightest part of the southwest rim in the X-ray energy band and contains the PWN. Conversely, we chose region B, about 4' apart from the PWN, to avoid contamination from non-thermal structures such as the PWN and arc. From these regions, source photons were accumulated using "evselect" and screened with the GTI filter mentioned above. For background subtraction, we selected another region labeled "BG" outside the SNR in Figure 2. After the background subtraction, we obtained 4613 events (MOS1)/4753 events (MOS2) and 4273 events (MOS1)/3943 events (MOS2) from regions A and B, respectively. Figure 6 shows the obtained X-ray spectra, both of which show several line features below 2 keV, while region A also shows a hard X-ray continuum above 2 keV that may have originated in the PWN and arc.
2) and "B" (r = 3') denoted in Figure 2. Region A is the brightest part of the southwest rim in the X-ray energy band and contains the PWN. Conversely, we chose region B, about 4' apart from the PWN, to avoid contamination from non-thermal structures such as the PWN and arc. From these regions, source photons were accumulated using "evselect" and screened with the GTI filter mentioned above. For background subtraction, we selected another region labeled "BG" outside the SNR in Figure 2. After the background subtraction, we obtained 4613 events (MOS1)/4753 events (MOS2) and 4273 events (MOS1)/3943 events (MOS2) from regions A and B, respectively. Figure 6 shows the obtained X-ray spectra, both of which show several line features below 2 keV, while region A also shows a hard X-ray continuum above 2 keV that may have originated in the PWN and arc.
Figure 6. Left: X-ray spectrum of region A with the best-fit model consisting of a VNEI model and a power-law function. Right: X-ray spectrum of region B fitted with a VNEI model. The best-fit parameters are summarized in Table 2.
Download figure:
Standard image High-resolution imageIn the spectral analysis of region B, we tried three thin-thermal plasma models: a non-equilibrium ionization (NEI) model and two equilibrium ionization models of MEKAL and APEC. To account for the line features, the metal abundances of Ne, Mg, Si, and Fe were set to be variable. The resulting best-fit parameters are summarized in Table 2. The three plasma models converged under similar conditions. The obtained high net infers that the diffuse plasma filling the SNR is in an ionization equilibrium state.
Table 2. Results of Spectral Fitting of Regions A and B
| Model | NH | kT | Metal Abundancea | net | EMb | Photon Index | Flux0.5-10 keVc | 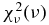 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1022 cm−2) | (keV) | Ne | Mg | Si | Fe | (cm−3 s) | (10−12erg s−1cm−2) | ||||
| Region A | |||||||||||
| NEI+PL | 0.35 ± 0.03 | 0.61 ± 0.03 | 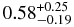 |
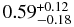 |
 |
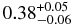 |
>4.4 × 1011 | 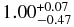 |
 |
1.46 ± 0.08 | 1.115 (139) |
| MEKAL+PL | 0.35 ± 0.05 | 0.61 ± 0.03 | 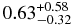 |
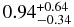 |
 |
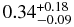 |
... | 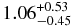 |
 |
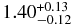 |
1.167 (140) |
| APEC+PL |  |
0.62 ± 0.03 |  |
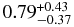 |
 |
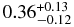 |
... |  |
 |
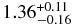 |
1.128 (140) |
| Region B | |||||||||||
| NEI | 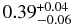 |
 |
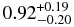 |
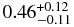 |
 |
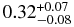 |
>3.5 × 1011 |  |
... | ... | 0.903 (61) |
| MEKAL | 0.34 ± 0.05 | 0.65 ± 0.03 | 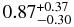 |
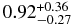 |
 |
 |
... | 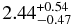 |
... | ... | 1.034 (61) |
| APEC | 0.36 ± 0.05 | 0.65 ± 0.03 |  |
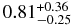 |
 |
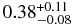 |
... |  |
... | ... | 0.891 (60) |
Notes. Errors are within a 90% confidence level.
aThe abundance of each metal is normalized by the solar abundance.
bEmission measure  , where DA is the angular diameter distance to the source (cm), and ne and nH (cm−3) are the electron and hydrogen densities, respectively.
cUnabsorbed energy flux of the power-law component over the energy range of 0.5–10 keV.
, where DA is the angular diameter distance to the source (cm), and ne and nH (cm−3) are the electron and hydrogen densities, respectively.
cUnabsorbed energy flux of the power-law component over the energy range of 0.5–10 keV.
Download table as: ASCIITypeset image
For region A, we employed two-component models consisting of a thermal plasma model and a power-law function that explains the high-energy continuum. Moreover, we found that the parameters of the thermal component were very similar to those of region B: a column density of NH = 3.5 × 1021 cm−2, a plasma temperature of kT = 0.61 keV, a relatively low Fe abundance below 0.4 in the solar abundance unit, and a high ionization parameter of net > 4 × 1011 cm−3 s. Conversely, the power-law function has a photon index of ∼1.8, which seems to be a reasonable value for a PWN (Kargaltsev & Pavlov 2008).
2.3.2. Point Source
Next, we tried to investigate the spectrum of the point source at the PWN apex with the Chandra data. To prevent photons from the SNR or PWN contaminating the spectrum of the point source, we selected a circular region centered on the point source with a radius of 3'', in which more than 90% of photons from a point source would be accumulated (Weisskopf et al. 2000b), while the background events were sampled from an annulus just around the source region (3'' < R < 20''). Subsequently, we extracted photons using "specextract" from the selected regions. After the background subtraction, we obtained 143 photons for a 0.5–10.0 keV energy band (the background contribution was 2.2%). The poor photon statistics meant that the column density could not be constrained by a simultaneous fitting. We therefore employed a fixed value of NH = 3.5 × 1021 cm−2 for the column density, based on the spectroscopy of region B shown above. In the spectral fitting of the point source, we examined the model functions of a power-law function and a blackbody, and obtained a photon index of Γ = 1.3 ± 0.3 and a temperature of kT = 0.8 ± 0.1 keV, respectively. In addition, we also tried to fit the spectrum with a mixture model of a blackbody and a power-law function, but could not attain reliable results for the limited photon statistics. The obtained X-ray spectrum is shown in Figure 7 with model functions, and the resultant parameters are summarized in Table 3. The results of the spectral analysis are summarized in Table 3.
Figure 7. X-ray spectrum of the point source at the PWN apex. The source photons were accumulated from a 3'' radius circular region centered on the point source. The background events were evaluated from an annulus just around the source region (3'' < R < 20''). The solid line shows the model function of the absorbed power-law function, while the dashed line shows the absorbed blackbody model. The best-fit parameters are summarized in Table 2.
Download figure:
Standard image High-resolution imageTable 3. Results of Spectral Fitting of the Point Source
| Model | NH | kTBB | Photon Index | Normalization |  |
|---|---|---|---|---|---|
| (1022 cm−2) | (keV) | ||||
| Power law | 0.35 (fixed) | ... | 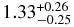 |
 a a |
1.036 (12) |
| Blackbody | 0.35 (fixed) |  |
... | 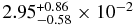 b b |
1.152 (12) |
Notes. Errors are within a 90% confidence level. aEnergy flux over the energy 0.5–10.0 keV in units of 10−14 erg s−1 cm−2. bSource radius in kilometers assuming the distance to the source to be 4.1 kpc.
Download table as: ASCIITypeset image
2.3.3. Spatially Resolved Spectroscopy of the PWN
To investigate the spectral evolution of the pulsar wind along the flow line, we performed a spatially resolved spectroscopy using the XMM data. For this purpose, we divided the PWN into seven rectangular regions with dimensions of 20'' × 100'', as shown in Figure 8. For each region, we then conducted a spectral fitting with a two-component model of an NEI model and a power-law function. The limited photon statistics prevent us from setting all the parameters free. Therefore, we employed fixed parameters: a column density of NH = 3.5 × 1021 cm−2, metal abundances (Ne = 0.58, Mg = 0.59, Si = 1.0, and Fe = 0.38), and an ionization parameter of net = 4.4 × 1011 s cm−3, according to the spectroscopy of region A.
Figure 8. Close-up view of the pulsar wind nebula in MSH 15−56 taken by XMM-Newton. Seven rectangular regions, each of dimension 20'' × 100'', are used to investigate the spatial variations of X-ray spectra.
Download figure:
Standard image High-resolution imageFigure 9 describes the photon index of the power-law component, the energy fluxes of the power-law component, and the energy flux of the thermal components as functions of distance from the PWN apex. Compared with the thermal component showing constant surface brightness, the power-law component seems to have originated in the PWN, and its photon index obviously steepens with increasing distance from the point source.
Figure 9. Results of the spatially resolved spectroscopy for rectangular regions marked in Figure 8 plotted as functions of distance from the pulsar. The top and middle panels show the photon indices and the unabsorbed flux of the power-law components, respectively, while the bottom panel shows the normalized surface brightness of the thermal component.
Download figure:
Standard image High-resolution image3. DISCUSSION
3.1. Ambient Environment of the PWN
PWN structures (i.e., a bow shock and a tail) are sensitive to the ambient conditions. Accordingly, we first clarify the environmental condition around the PWN in MSH 15−56. Based on the spectroscopy of region A, the hot gas in the SNR seems almost to be in an ionization equilibrium condition with an ionization parameter of net ⩾ 4.4 × 1011 s cm−3. Assuming that the emitting region is an oblate ellipsoid, the emitting volume amounts to V = (4/3)π d3(3 2 × 3
2 × 3 2 × 1
2 × 1 2) ∼ 2.6 × 1057 cm3. Adopting the emission measure listed in Table 2, the number density of the plasma can be estimated, and we have np ∼ 0.28f−1/2(d/4.1 kpc)−1/2 cm−3, where f is a filling factor. Comparing the lower limit of net with this number density, we obtained a lower limit of the ionization timescale, τion > 50f1/2 kyr, which exceeded the dynamic SNR age τ ∼ 15 kyr to some extent (Kassim et al. 1993). If that is due to the overestimation of the emitting volume, then the filling factor f should be smaller than 0.1.
2) ∼ 2.6 × 1057 cm3. Adopting the emission measure listed in Table 2, the number density of the plasma can be estimated, and we have np ∼ 0.28f−1/2(d/4.1 kpc)−1/2 cm−3, where f is a filling factor. Comparing the lower limit of net with this number density, we obtained a lower limit of the ionization timescale, τion > 50f1/2 kyr, which exceeded the dynamic SNR age τ ∼ 15 kyr to some extent (Kassim et al. 1993). If that is due to the overestimation of the emitting volume, then the filling factor f should be smaller than 0.1.
Evolutions of SNRs depend on the number density of the ambient medium. Blondin et al. (1998) calculated the transition time from the Sedov phase to the pressure-driven snowplow (PSD) phase:
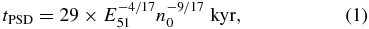
where E51 is the explosion energy in units of 1051 erg. At that moment, the SNR radius achieves  cm, which corresponds to
cm, which corresponds to  . Our subsequent analysis for the PWN will show that the pulsar remains inside the SNR, though its velocity exceeds 1000 km s−1, which implies that the age should be less than 21 kyr. To end the Sedov phase within 21 kyr, we need n0 > 1.8 cm−3, which contradicts the large SNR radius observed. Therefore, we conclude that the SNR MSH 15−56 is presumed to be still in the Sedov phase.
. Our subsequent analysis for the PWN will show that the pulsar remains inside the SNR, though its velocity exceeds 1000 km s−1, which implies that the age should be less than 21 kyr. To end the Sedov phase within 21 kyr, we need n0 > 1.8 cm−3, which contradicts the large SNR radius observed. Therefore, we conclude that the SNR MSH 15−56 is presumed to be still in the Sedov phase.
The temperature of the hot gas filling the SNR is 0.61 keV, and hence the sonic velocity in the gas is  km s−1, where γ is the specific heat ratio (γ = 5/3 for mono-atomic gas), mp is the proton mass, and μ is the mean molecular weight.
km s−1, where γ is the specific heat ratio (γ = 5/3 for mono-atomic gas), mp is the proton mass, and μ is the mean molecular weight.
3.2. Point Source
For the point source at the PWN apex, we performed spectroscopy using the Chandra data. However, the poor photon statistics prevented us from distinguishing the radiative processes, blackbody, synchrotron, or a mixture thereof. With a single blackbody model, we obtained a temperature of ∼0.8 keV, which appears unfeasibly high compared with the standard NS cooling model that predicts that a 10 kyr old isolated neutron star could not radiate in an X-ray energy band (Shapiro & Teukolsky 1986). It should also be noted that there are several counterexamples of the standard model, such as the Vela pulsar (τ ∼ 11 kyr) and Geminga (τ ∼ 500 kyr), that emit thermal X-rays. It is therefore difficult to reject the possibility of thermal emission from the pulsar in MSH 15−56 at this moment. Dickel et al. (2000) proposed that the point source should be a magnetar to explain the position gap between the hard X-ray PWN and the radio plerion. The known magnetar candidates show high-temperature blackbody components up to 0.7 keV (Woods & Thompson 2006), but the obtained source radius of ∼0.02 km, which corresponds to  erg s−1, is uncomfortably small for a magnetar candidate such as the anomalous X-ray pulsars.
erg s−1, is uncomfortably small for a magnetar candidate such as the anomalous X-ray pulsars.
In contrast, the power-law model provided parameters. The obtained power-law index, ΓPSR ∼ 1.33 ± 0.26, is consistent with the previous analysis reported in Plucinsky et al. (2002) and is a typical value for a pulsar accompanied by a PWN. In addition, the pair of photon indices of the point source and the entire PWN match the empirical correlation, ΓPWN = 0.86 + 0.72ΓPSR, as reported by Gotthelf (2003). It should be noted that the point source appears slightly extended with a size of 1 7 in FWHM. Therefore, the spectral data of the point source also contain X-rays from the extended component just around the pulsar, and it is difficult to eliminate this contamination even with Chandra.
7 in FWHM. Therefore, the spectral data of the point source also contain X-rays from the extended component just around the pulsar, and it is difficult to eliminate this contamination even with Chandra.
The X-ray luminosity of the point source amounts to  erg s−1 cm−2 for the 0.5–10.0 keV energy band. Assuming that the non-thermal emission from region A is accounted for by the sum of the point source and the PWN, the flux ratio between the point source and the PWN is about 3%. Kargaltsev et al. (2007) claimed that the luminosities of PWNe and pulsars showed a power-law correlation. Particularly for middle-aged pulsars with non-thermal luminosities within the range 1031 erg s−1 < LPSR < 1034 erg s−1, the relation can be effectively described by a power-law function, log LPWN = 0.89log LPSR + 4.2 (or simply LPWN = 5LPSR). Compared with those samples in Kargaltsev et al. (2007), the point source in MSH 15−56 is about one order of magnitude fainter than the expected luminosity for its PWN. It should be noted that the luminosities of some PWNe listed in Kargaltsev et al. (2007) can be underestimated because their large-scale components are too faint to be seen. If that is the case, then the luminosity ratio LPWN/LPSR may be more reasonable.
erg s−1 cm−2 for the 0.5–10.0 keV energy band. Assuming that the non-thermal emission from region A is accounted for by the sum of the point source and the PWN, the flux ratio between the point source and the PWN is about 3%. Kargaltsev et al. (2007) claimed that the luminosities of PWNe and pulsars showed a power-law correlation. Particularly for middle-aged pulsars with non-thermal luminosities within the range 1031 erg s−1 < LPSR < 1034 erg s−1, the relation can be effectively described by a power-law function, log LPWN = 0.89log LPSR + 4.2 (or simply LPWN = 5LPSR). Compared with those samples in Kargaltsev et al. (2007), the point source in MSH 15−56 is about one order of magnitude fainter than the expected luminosity for its PWN. It should be noted that the luminosities of some PWNe listed in Kargaltsev et al. (2007) can be underestimated because their large-scale components are too faint to be seen. If that is the case, then the luminosity ratio LPWN/LPSR may be more reasonable.
Nonetheless, the observed LPWN/LPSR ratio resembles that of the Vela pulsar, which is also unusually underluminous in X-rays (Pavlov et al. 2001b). Considering previous pulsar studies, the non-thermal model provided the relatively reliable and appropriate parameters expected for a middle-aged Vela-like pulsar.
Despite expectations (Kaspi et al. 1996), no pulse emission from the point source has been detected in any observable energy bands. We therefore try to estimate the spin-down luminosity  using an empirical relation between the spin-down luminosity and the X-ray luminosity of the entire nebula (Seward & Wang 1988; Becker & Truemper 1997; Kawai et al. 1998; Kargaltsev et al. 2007). In this study, we employed one of the most recent model functions for pulsar–PWN systems based on Chandra and XMM data,
using an empirical relation between the spin-down luminosity and the X-ray luminosity of the entire nebula (Seward & Wang 1988; Becker & Truemper 1997; Kawai et al. 1998; Kargaltsev et al. 2007). In this study, we employed one of the most recent model functions for pulsar–PWN systems based on Chandra and XMM data,  for 0.5–10.0 keV (Kanai 2010), and found a spin-down luminosity of
for 0.5–10.0 keV (Kanai 2010), and found a spin-down luminosity of  erg s−1. The obtained
erg s−1. The obtained  is almost equivalent to that of the Vela pulsar,
is almost equivalent to that of the Vela pulsar,  erg s−1 (Pavlov et al. 2001a and references therein). Moreover, Gotthelf (2003) reported another relation between the spin-down luminosity and the spectral index of PWN,
erg s−1 (Pavlov et al. 2001a and references therein). Moreover, Gotthelf (2003) reported another relation between the spin-down luminosity and the spectral index of PWN,  , where
, where  is the spin-down energy in units of 1040 erg s−1. Substituting ΓPWN = 1.7 into the formula yields
is the spin-down energy in units of 1040 erg s−1. Substituting ΓPWN = 1.7 into the formula yields  erg s−1. However, the recent studies on PWNe accompanied by pulsars with known
erg s−1. However, the recent studies on PWNe accompanied by pulsars with known  revealed that the relation of
revealed that the relation of  shows very large scatter up to four orders of magnitude with respect to the best-fit relations (Cheng et al. 2004; Li et al. 2008; Kargaltsev & Pavlov 2010). Moreover, Arzoumanian et al. (2011) discovered a PWN around PSR J2022+3842 that has an unusually low conversion efficiency of spin-down power to X-ray luminosity and concluded that the
shows very large scatter up to four orders of magnitude with respect to the best-fit relations (Cheng et al. 2004; Li et al. 2008; Kargaltsev & Pavlov 2010). Moreover, Arzoumanian et al. (2011) discovered a PWN around PSR J2022+3842 that has an unusually low conversion efficiency of spin-down power to X-ray luminosity and concluded that the  relation proposed earlier may not apply for many young pulsars. Therefore, discovery of the pulse emission is required for more quantitative discussions.
relation proposed earlier may not apply for many young pulsars. Therefore, discovery of the pulse emission is required for more quantitative discussions.
3.3. Estimation of the Proper Motion Velocity
Chandra and XMM-Newton revealed detailed structures of the PWN in MSH 15−56: a point source accompanied by a wedge-shaped broad tail extending ∼2' from the apex. The tail is extended and directed at the center of the SNR. Obviously, the observed PWN is analogous to the bow shock PWN running supersonically in the ISM, as reported in dozens of previous studies.
Currently, we know the precise position of the point source that can be the pulsar driving the PWN. The pulsar is ∼13' apart from the SNR centroid and the offset angle corresponds to 2.4 × 1019 cm for d = 4.1 kpc. If the pulsar was kicked by the SN explosion that generated MSH 15−56, then the proper motion velocity of the pulsar would be easily calculated by dividing the travel distance by the SNR age. Incidentally, we must take into account the inclination angle i between the direction of proper motion and the line of sight as shown in Figure 10, because the observed image is only a projection of three-dimensional structures on the celestial plane. Subsequently, we have a formula for the proper motion velocity5 of the pulsar,
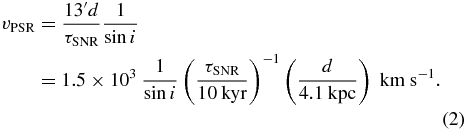
Since the above relation depends on the parameters of distance d, the SNR age τSNR, and the inclination angle i, which may contain large errors, the resulting velocity seems rather uncertain.
Figure 10. Schematic image of the geometry of the SNR–PWN system of MSH 15−56. The inclination angle i is defined by the angle between the direction of the pulsar's proper motion and the line of sight. If i > 44°, then the PWN must be in the SNR (a) and if i < 44°, then the PWN should be outside the SNR (b).
Download figure:
Standard image High-resolution imageWe can also approach the proper motion of the pulsar based on the observed structures of the PWN. While simple analyses (Chen et al. 1996; Wilkin 1996) indicate that the bow shock structure should be collimated toward the tail, the observed tail seems to have a constant opening angle θapp. Accordingly, we interpret this structure as a Mach cone; plasmas left behind from the PWN subsequently expand at the speed of sound, whereupon the surface of such plasma forms a conical structure as discussed in Chevalier & Reynolds (2011). If the surface of the PWN propagates in a medium with sonic speed cs, then the opening angle of the PWN θ should follow

where vrel is the proper motion velocity with respect to the surrounding material. Here, we have two options for cs: one is cs, ISM ∼ 15 km s−1 for the PWN already outside the SNR, and the other is cs, SNR ∼ 440 km s−1 for the PWN remaining in the SNR.
In the former case, we can set vrel ≃ vPSR. The inclination angle i should exceed the apparent opening angle θapp ∼ 25°, because we can see the wedge-shaped bow shock (see Figure 3), and it also be smaller than ≃ 44° to have the PWN outside the SNR, as shown in Figure 10(b). Taking into account the effect of the inclination angle i, Equation (3) can be rewritten as
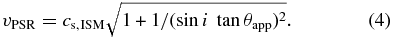
The constraint of the inclination angle, i > 25°, requires a proper motion of vPSR < 80 km s−1. If this is the case, then the travel time of the pulsar from the birthplace to the current location will be unfeasibly long, ∼260 kyr, which is one order of magnitude longer than the SNR age reported in past studies. Therefore, the PWN is likely still inside the SNR and the inclination angle should be within the range 44° < i < 90°, as shown in Figure 10(a). Even if we neglect the motion of gas inside the SNR and use Equation (4), i = 90° gives a lower limit, vPSR > 1000 km s−1. Taking into account the flow velocity of the downstream behind the SNR forward shock, the relative velocity is set at vrel = vPSR − vHG, where vHG is the velocity of the shock-heated gas behind the SNR forward shock. If the SNR is currently in the Sedov phase, meaning that the expansion velocity follows vSNR = (2/5)RSNR/τSNR, then we determine the velocity of the shock-heated gas behind the SNR forward shock to be vHG = (3/4)vSNR by assuming the strong shock condition (van der Swaluw et al. 2001). Consequently, the proper motion velocity can be written as
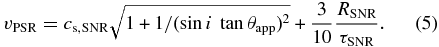
Note that the above equation also depends on uncertain parameters of τSNR and i as in Equation (2). By combining Equations (2) and (5), we can separate the variables vPSR and τSNR as follows:
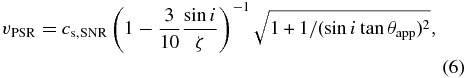
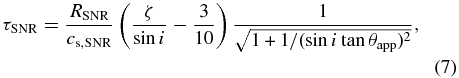
where ζ ≡ 13'/18' is the distance from the SNR centroid to the pulsar in units of the SNR radius. Figure 11 shows the resulting pulsar's proper motion velocity and the age of the SNR as functions of the inclination angle i for various θapp. The proper motion of the pulsar is within the range vPSR = 1900 ± 100 km s−1, which is about five times faster than the typical kick velocity of known pulsars (Frail et al. 1994). Meanwhile, the SNR age should be 9800 ± ∼ 1200 yr for θapp ∼ 25°. By substituting the current status of the SNR, RSNR = 18' and τSNR = 9.8 kyr, into the Sedov solution, the density of the ISM surrounding the SNR can be constrained as
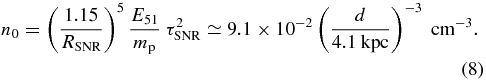
The number density of the surrounding material and that of the compressed ISM in the SNR (np = 0.28 cm−3) seem to follow the jump condition of the strong shock. Although the distance to the object remains unclear, the SNR age obtained seems reasonable when compared with past estimations. Moreover, although the obtained pulsar velocity is relatively fast, it remains in an acceptable range according to past pulsar studies.
Figure 11. Pulsar velocity and age of MSH 15−56 as functions of inclination angle i for the case in which the PWN remains in the SNR. The velocities were calculated from the relation between the opening angle of the bow shock and the velocity of the proper motion (Equation (5)), while the SNR age was estimated from Equation (7). The dotted, solid, and dashed lines represent opening angles of θapp = 22 5, 25°, and 27
5, 25°, and 27 5, respectively. The shaded area is forbidden by geometrical constraints as shown in Figure 10.
5, respectively. The shaded area is forbidden by geometrical constraints as shown in Figure 10.
Download figure:
Standard image High-resolution image3.4. Pulsar Wind Termination Shock
Assuming an isotropic pulsar wind in the pulsar rest frame, the ram pressure should balance the pulsar wind,

where  is the radius of the forward termination shock from the pulsar, ρ is the mass density of the ambient matter, and vrel is the pulsar's velocity with respect to the surrounding material. As shown in Figure 12, the standoff distance of the backward termination shock
is the radius of the forward termination shock from the pulsar, ρ is the mass density of the ambient matter, and vrel is the pulsar's velocity with respect to the surrounding material. As shown in Figure 12, the standoff distance of the backward termination shock  is thought to be elongated because the bow shock becomes rather weak on this side, the ratio of the standoff distances between the forward and backward termination shocks follows
is thought to be elongated because the bow shock becomes rather weak on this side, the ratio of the standoff distances between the forward and backward termination shocks follows
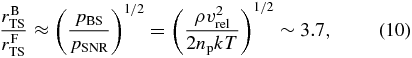
where pBS is the pressure at the bow shock and pSNR is the internal pressure of the SNR (Bucciantini 2002; van der Swaluw et al. 2001). The current expanding velocity of the SNR can be derived with the Sedov solution, vSNR = 2/5(RSNR/τSNR) ∼ 860 km s−1 for τSNR = 9.8 kyr. Therefore, the relative velocity between the pulsar and its surroundings is vrel = vPSR − (3/4)vSNR ∼ 1300 km s−1. Adopting the number density inside the SNR np = 0.28 cm−3, the mass density becomes ρ ∼ 4.7 × 10−25 g cm−3. Therefore, the entire length of the termination shock becomes  , which can be resolved by Chandra. In fact, the obtained image of the point source seems to exceed the PSF slightly, although the ellipticity is uncertain. The measured size of the coma is about 1
, which can be resolved by Chandra. In fact, the obtained image of the point source seems to exceed the PSF slightly, although the ellipticity is uncertain. The measured size of the coma is about 1 7 ± 0
7 ± 0 4 in FWHM, which reveals another constraint on the spin-down luminosity of the pulsar,
4 in FWHM, which reveals another constraint on the spin-down luminosity of the pulsar,  erg s−1, which seems to be one order of magnitude smaller than the inferred value based on the empirical relation shown above.
erg s−1, which seems to be one order of magnitude smaller than the inferred value based on the empirical relation shown above.
Figure 12. Schematic view of the assumed SNR–PWN system.
Download figure:
Standard image High-resolution image3.5. Spectral Variations
As shown in Figure 9, the spectral index ΓPWN steepens from 1.7 to 2.5 with increasing distance from the point source. The spectral evolution can be explained by synchrotron cooling or adiabatic cooling, hence we can conclude that the point source at the PWN apex drives the entire PWN, although no pulsation has been detected at this moment.
Let us assume that the shocked pulsar wind balances the pressure of the gases within the SNR, whereupon the flow velocity of the pulsar wind will be constant. Here, we applied a theoretical model proposed by Tanaka & Takahara (2010), who assumed that the PWN is expanding at constant velocity, to the bow shock nebula in which relativistic gas is flowing at vrel and expanding within the bow shock. For simplicity, we also assumed a constant opening angle of the bow shock that bounds the shocked pulsar wind. In this model, a volume element at r(t) = vrelt from the pulsar is expressed as dV = Ωr(t)2dr, where dr is the thickness of the volume element and Ω is the solid angle of the bow shock. So the energy loss of the relativistic electrons is
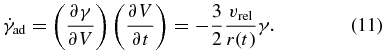
Meanwhile the relativistic electrons also lose their energy via synchrotron radiation. The radiation loss is
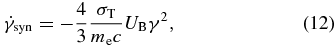
where γ is the Lorentz factor of relativistic electrons, σT is the Thomson cross-section, UB is the magnetic energy density, and me is the electron mass.
Subsequently, we compare the cooling times of these processes focusing on the rectangular region "C" (Figure 8), just upstream of the point where the spectral index changes. Here, we assumed that the shocked pulsar wind in region C could be in an equipartition condition and the emitting volume is a cylinder of length 20'' and radius 20'' that corresponds to ∼5.8 × 1054 cm3 for a distance of 4.1 kpc. The spectral fitting (Figure 9) yielded a photon index, ΓPWN = 1.7, and an unabsorbed energy flux of the power-law component, 4.2 × 10−13 erg s−1 cm−2, for this region. We therefore infer that the spectral luminosity at 1 keV is L1 keV = 8.9 × 1014 erg s−1 Hz−1. Based on the equipartition argument (Longair 1994), we can constrain the minimum energy of the electrons and magnetic field in this region,
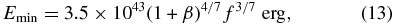
where f is the filling factor and β describes the energy contribution from protons and heavy ions. The obtained energy density corresponds to a magnetic field of B ∼ 26 μG in the equipartition condition. The cooling timescale for a relativistic electron emitting synchrotron X-rays with energy  is therefore
is therefore
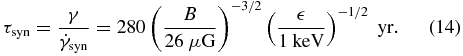
The adiabatic expansion also cools the relativistic electrons, although it does not change the spectral index since the process does not depend on the electrons' energy. Based on Equation (11), we can obtain the timescale of adiabatic cooling,
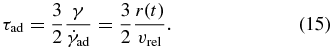
The cooling timescale is therefore about 900(1/sin i) yr for r(t) = 40'' and vrel = 1300 km s−1. The obtained timescale is longer than the cooling timescale of synchrotron estimated above, but is still not negligible.
Meanwhile, in terms of dynamics, the relativistic electrons in region C travel ∼30'' while cooling, hence the photon index steepens by ΔΓ = 0.5. Adopting a transverse pulsar velocity with respect to the surrounding SN ejecta vrel ∼ 1300 km s−1, a we obtain travel time of τdyn = 450 yr, which is consistent with the synchrotron cooling time obtained above.
3.6. Magnetization of the Pulsar Wind
The magnetization parameter σ of the pulsar wind just upstream of the termination shock can be estimated from the ratio of the termination shock radius to the size of the PWN. Since the shock transforms the kinetic energy  kin of the pulsar wind into the internal energy
kin of the pulsar wind into the internal energy  int, σ can be rewritten as follows:
int, σ can be rewritten as follows:
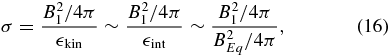
where B1 is the toroidal magnetic field just upstream of the shock and BEq is the equipartition magnetic field after the shock (Shibata et al. 1998). With the assumption of a toroidal magnetic field around the pulsar, combining the equations of continuity ( ) and the conservation law of magnetic flux (rTS cB1 = rnvnBEq) yields
) and the conservation law of magnetic flux (rTS cB1 = rnvnBEq) yields

Substituting the backward shock radius,  , and the radius of the nebula rn = 20'' that corresponds to the distance from the pulsar to the brightest point at which the pulsar wind achieves equipartition, we found σ ∼ 3 × 10−3. The obtained magnetization is about one order of magnitude smaller than that for the Crab pulsar σcrab = 0.03 (Mori 2002) and that for PSR B1509−58 σB1509 = 0.01 (Yatsu et al. 2009), which were calculated in the same manner, though it effectively matches that for the Crab pulsar based on traditional estimation using expansion velocity (Kennel & Coroniti 1984).
, and the radius of the nebula rn = 20'' that corresponds to the distance from the pulsar to the brightest point at which the pulsar wind achieves equipartition, we found σ ∼ 3 × 10−3. The obtained magnetization is about one order of magnitude smaller than that for the Crab pulsar σcrab = 0.03 (Mori 2002) and that for PSR B1509−58 σB1509 = 0.01 (Yatsu et al. 2009), which were calculated in the same manner, though it effectively matches that for the Crab pulsar based on traditional estimation using expansion velocity (Kennel & Coroniti 1984).
3.7. Non-thermal Emission from the Rim of the SNR Rim
We found a non-thermal X-ray filament nearby the PWN, despite its old age and hence relatively slow shock velocity. Here, we confirm whether or not the emission from the filament can be explained by shock acceleration. The limited photon statistics mean that we could not investigate precise spectral parameters, but the filament seems to emit X-rays up to a few keV (Figure 2). We therefore assumed a power-law spectrum of accelerated electrons with an exponential cutoff at Emax, N(E)∝E−pexp (E/Emax) based on Aharonian & Atoyan (1999). Moreover, these electrons emit synchrotron radiation with a peak energy of
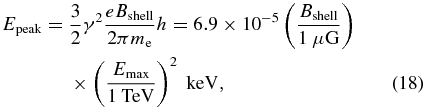
where Bshell is the magnetic field in the emitting region. If we assume Epeak = 0.1 keV, then the pair of Emax and Bshell can be constrained as
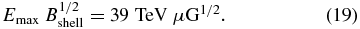
To solve Emax and Bshell independently, we took into account the shell width.
First, we assumed that the non-thermal emission originates upstream of the shock where the electrons are trapped and accelerated to relativistic velocity. According to Bamba et al. (2003), the magnetic field and maximum energy of the electrons can be estimated using the width of the rising edge. In this study, we employed a width of the outer edge Δr = 10'' that corresponds to ∼6.1 × 1017 cm and a shock velocity of vSNR = 860 km s−1. It should be noted that the photon statistics of the X-ray image were too poor to resolve the accelerated particles spreading upstream of the shock, therefore the Δr in this argument is only an upper limit. If the shell width is determined by competition between the advection and diffusion of electrons upstream of the shock, then the diffusion coefficient D can be written as follows:
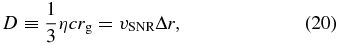
where η is the ratio of the mean free path to the gyro radius, the so-called gyrofactor, and rg = (Emax/eBshell) is the gyroradius. Combined with Equation (19), we found the maximum energy of the electron and the upstream magnetic field of the shock,
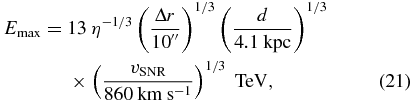
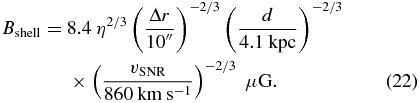
Based on the theory of diffusive shock acceleration, we can estimate the time to accelerate electrons up to the energy required to emit X-ray photons,
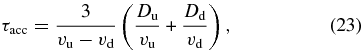
where Du and Dd are the diffusion coefficients defined in Equation (20) for upstream and downstream, respectively, and vu is the downstream flow velocity in the shock rest frame. Since we do not know the magnetic field just above the shock where the magnetic field may be amplified by turbulence, we therefore roughly assumed Du = Dd = Emaxcη/(3eBshell), while employing the jump condition for the flow velocity, vu = 4vd(= vSNR). Adopting those assumptions, we obtain
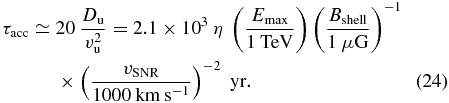
For Emax = 13 TeV and Bshell = 8.4 μG, the acceleration time becomes
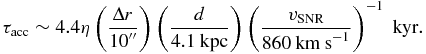
Conversely, the cooling time due to the synchrotron radiation limits the maximum energy of the electron, and thus should exceed the acceleration time shown above. The cooling time for the electrons with given energy Emax and a magnetic field Bshell can be written as

Substituting Equations (21) and (22) into the above formula, we obtain a cooling time of
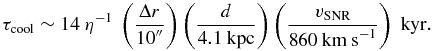
The above estimations are based on the width of the non-thermal shell shown in Figure 3 that is relatively unclear, therefore the obtained τacc and τcool may be lower and upper limits, respectively. Nevertheless, the obtained cooling time τcool seems longer than τacc, and the result thus supports the fact that the discovered thin X-ray filament can be explained by synchrotron emission from the shock front of the SNR.
The width of the non-thermal filament can also be interpreted as competition between the flow velocity and the cooling time of the electrons downstream of the shock, τcool ≃ Δr/vd ∼ 900 yr. Substituting 4vd = vSNR and Equation (25), the possible pair of Emax and Bshell is constrained as
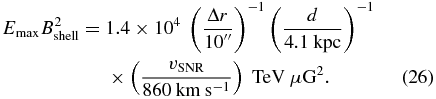
Subsequently, combining the above equation with Equation (19), we obtain

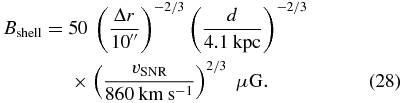
The obtained magnetic field Bshell is somewhat large for an SNR but still seems acceptable because the magnetic field at the brightest vicinity in MSH 15−56 at a radio energy band amounts to 45 μG (Dickel et al. 2000). If we take an upstream magnetic field of BISM = Bshell/4 ∼ 13 μG using a conservative estimate, then the acceleration time can be evaluated from Equation (24),
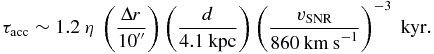
The obtained value is comparable to a cooling time of τcool ∼ 900 yr, although that is one order of magnitude shorter than the estimation based on Bamba et al. (2003). Consequently, these estimations based on two different scenarios both support the existence of synchrotron electrons around the shock front.
4. CONCLUSION
We presented a detailed study of the PWN in MSH 15−56 utilizing the archive data taken with XMM-Newton and Chandra. Our main findings are as follows.
- 1.The south rim of MSH 15−56 is filled by equilibrium ionization plasma with a temperature of kT = 0.61 keV and a number density of np = 0.28 cm−3. In the Sedov phase, the SNR seems to be expanding at 860 km s−1 in a low density ISM of np ∼ 0.91 cm−3.
- 2.The PWN in MSH 15−56 has a cometary morphology as seen in bow shock PWNe running through the ISM supersonically. Since the tail directs the center of the SNR, it is inferred that the PWN and SNR have the same progenitor star. The apparent half opening angle of the tail is about θapp = 25°, indicating that the PWN is running at Mach number
 and remains in the SNR. This means that the PWN is running at ∼1900 km s−1. Comparing the travel velocity of the PWN and the expansion velocity of the SNR, the system age is constrained within the range 9800 ± 1100 yr.
and remains in the SNR. This means that the PWN is running at ∼1900 km s−1. Comparing the travel velocity of the PWN and the expansion velocity of the SNR, the system age is constrained within the range 9800 ± 1100 yr. - 3.At the PWN apex, Chandra detected a point source showing a power-law spectrum with a photon index of Γ = 1.3. The spatially resolved spectroscopy revealed that the photon index of the PWN steepens from 1.7 to ∼2.5 along the flow line from the apex toward the tail. This result implies that the PWN is powered by the point source, although there is no evidence of pulsation from the object.
- 4.The flux ratio of the pulsar candidate to the PWN is about 3%, which is about one order of magnitude smaller than that for the other pulsar–PWN pairs but resembles the Vela pulsar. We also estimate the spin-down luminosity of the unseen pulsar using an empirical relation at
 erg s−1, which is again almost equivalent to that of the Vela pulsar. The spectrum, luminosity, and estimated spin-down luminosity imply that the unseen pulsar should be a Vela-like pulsar. Conversely, the size of the point source slightly exceeds the PSF of the HRMA. Assuming that the extended bright core corresponds to the shock front at which the pulsar wind is terminated, the pulsar's spin-down luminosity is also estimated to be 1.5 × 1036 erg s−1, which is about one order of magnitude smaller than that from the empirical relation and, moreover, only an upper limit. To constrain the energetics, the discovery of the pulse emission is strongly desired.
erg s−1, which is again almost equivalent to that of the Vela pulsar. The spectrum, luminosity, and estimated spin-down luminosity imply that the unseen pulsar should be a Vela-like pulsar. Conversely, the size of the point source slightly exceeds the PSF of the HRMA. Assuming that the extended bright core corresponds to the shock front at which the pulsar wind is terminated, the pulsar's spin-down luminosity is also estimated to be 1.5 × 1036 erg s−1, which is about one order of magnitude smaller than that from the empirical relation and, moreover, only an upper limit. To constrain the energetics, the discovery of the pulse emission is strongly desired. - 5.On the edge of the SNR and just near the PWN, a thin (∼10'') X-ray filament was discovered. Although the SNR is almost 10 kyr old, the diffusive shock acceleration model can support the synchrotron emission from the SNR rim that is expanding at 860 km s−1. The physical relationship and velocity differential between the pulsar candidate (vPSR ∼ 1900 km s−1) and the shell of the SNR (vshell ∼ 860 km s−1) suggest that the pulsar and its PWN are going to run through the blast wave in the near future.
The main conclusions, i.e., the Sedov phase SNR and very high-velocity pulsar, are based on the assumption that the wedge-shaped tail observed in the X-ray is a trail of electron–positron plasma ejected from the pulsar moving at supersonic speed. We have postulated that the tail corresponds to the Mach cone. If a different interpretation is proposed for the tail, then the scenario may be altered. However, the low-density ISM required to agree with the Sedov phase is consistent with the density within the SNR. Moreover, the age τSNR and expansion velocity vSNR obtained from the Sedov solution seem to be consistent with the non-thermal emissions from the SNR shock, as discussed in Section 3.7. The several properties concerning the X-ray luminosities of the pulsar and PWN resemble those for Vela, whose age resembles what we estimated here.
We are deeply grateful to J. Dickel and P. Plucinsky for giving us beautiful radio images, and to the referee for helpful comments. Y.Y. is grateful to S. Katsuda (Riken), S. Eguchi, H. Kishimoto, T. Koide, S. Takeuchi, F. Nakamoto, and Y. Shinohara (MITSUBISHI Electric) for valuable discussions. This work is based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and the USA (NASA) and data obtained from the Chandra Data Archive and software provided by the Chandra X-Ray Center (CXC) in the application packages CIAO.
Facilities: XMM (MOS) - Newton X-Ray Multimirror Mission satellite, CXO (ACIS) - Chandra X-ray Observatory satellite
Footnotes
- 4
- 5
Note that the obtained velocity of the pulsar is about five times larger than 410 km s−1 reported by Temim et al. (2013). This discrepancy may arise from the different assumptions of the pulsar birthplace, the age of the SNR, and the radial velocity of the pulsar.