EVOLUTION OF THE AXIAL MAGNETIC FIELD IN SOLAR FILAMENT CHANNELS

The filament channel is a volume along the polarity inversion line that separates areas of opposite magnetic polarity on the Sun. A key observational condition for solar filament formation is photospheric flux cancellation at the polarity inversion line toward which opposite-polarity magnetic fields converge (see Martin 1998 and references therein). Thus, photospheric cancellation is the essential process in the formation of solar filaments (for a review, see Martin et al. 2008). Numerous detailed observations and theoretical arguments support the viewpoint that magnetic reconnection in the photosphere is the mechanism of cancellation (e.g., Martin 1990; Chae et al. 2002; Wood & Martens 2003; Park et al. 2009).

Theoretical models also demonstrate that convergence and reconnection of initially unconnected magnetic bipoles can lead to the formation of the observed large-scale structure of filaments (e.g., Martens & Zwaan 2001; Welsch et al. 2005; Litvinenko & Wheatland 2005). Calculations of the upward mass flux in the reconnection jets, associated with photospheric cancellation, show that the jets can be the main source of mass for filament formation. The mass for a large solar filament, for instance, can be supplied by cancellation in a few photospheric patches over several hours (e.g., Litvinenko et al. 2007). These theoretical results corroborate the observationally motivated picture in which cool plasma is injected into filaments by magnetic reconnection occurring near the solar surface (Wang 2001). Note for clarity, however, that the photospheric reconnection model has not yet been able to answer the difficult question of whether the injected mass can actually reach the heights at which quiescent solar filaments are observed.

The rate of formation of filament channels and filaments should increase if the rate of photospheric magnetic reconnection increases. Faster reconnection would imply that the magnetic field component B_⊥ perpendicular to the solar surface would be observed to cancel faster. Theoretical models of photospheric magnetic reconnection typically focus on the evolution of the canceling field component (Litvinenko 1999; Litvinenko & Martin 1999; Litvinenko et al. 2007). Wang & Muglach (2007) recently argued, however, that the channel formation rate also increases in the presence of a stronger magnetic field along the channel. Their analysis was based on the comparison of magnetograms from the Michelson Doppler Imager and the Hα filtergrams showing the orientation of Hα fibrils near the polarity inversion line. Because the fibrils are generally thought to follow the horizontal component of the chromospheric magnetic field, Wang & Muglach (2007) interpreted the degree of alignment of the fibrils as a measure of the axial magnetic field strength and concluded that the process of filament channel formation is accelerated when the axial field component B_|| is comparable to B_⊥. Notably, recent laboratory experiments demonstrate the effect of the axial field enhancement due to its transport by reconnection flows in the process of a current sheet formation (Frank et al. 2009). Faster accumulation of the nonreconnecting axial field in the sheet would imply a correspondingly faster rate of reconnection.

These considerations suggest that a relationship exists between the magnitude of the axial nonreconnecting magnetic field in a filament channel and the speed of reconnection inflow. The purpose of this paper is to quantify this relationship by calculating the evolution of the axial magnetic field in the course of reconnection. A magnetohydrodynamic (MHD) model for magnetic merging in a steady stagnation-point flow is formulated (Section 2), and an exact analytical solution is obtained for the axial magnetic field profile as a function of time and an arbitrary initial profile (Section 3). Specifying the initial profile leads to an expression for the maximum magnetic field in the channel as a function of the reconnection inflow speed. The results are utilized to argue that the maximum axial magnetic field in the channel can serve as an indicator of the photospheric reconnection rate (Section 4).

In what follows, the photospheric velocity v and magnetic field B are determined by solving the time-dependent incompressible resistive MHD equations that include the momentum equation

$$\begin{equation} \partial _t {\bf v} + ({\bf v} \cdot \nabla) {\bf v} = - \nabla p + (\nabla \times {\bf B}) \times {\bf B}, \end{equation} \tag{ 1 }$$

the induction equation

$$\begin{equation} \partial _t {\bf B} = \nabla \times ({\bf v} \times {\bf B}) + {\eta } {\nabla ^2} {\bf B}, \end{equation} \tag{ 2 }$$

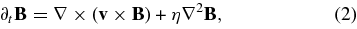
the continuity equation

$$\begin{equation} \nabla \cdot {\bf v} = 0, \end{equation} \tag{ 3 }$$

and Maxwell's equation

$$\begin{equation} \nabla \cdot {\bf B} = 0. \end{equation} \tag{ 4 }$$

These standard MHD equations are written in dimensionless form by adopting reference values of the magnetic field B₀, plasma density ρ₀, and length L. The Alfvén speed $v_{\rm A} = B_0 / \sqrt{4 \pi \rho _0}$ is the reference speed, and t_A = L/v_A is the reference time. The dimensionless parameter η is the electric resistivity, normalized by 4πv_AL/c².

Incompressibility may seem a questionable assumption in a strongly stratified solar photosphere and chromosphere. Note, however, that the vertical extent L of the current layer cannot exceed the atmospheric pressure scale height by a large factor, implying that compressibility has a relatively minor effect on the structure of the photospheric reconnection region (Litvinenko 1999; Litvinenko et al. 2007). Furthermore, the plasma speed decreases as the reconnection flow approaches a stagnation point, implying that compressibility can be neglected sufficiently close to the reconnection site.

An exact analytical solution can be given for time-dependent magnetic merging in a three-dimensional stagnation-point flow. An idealized model that is a locally valid approximation to a large class of velocity and magnetic fields is illustrated in Figure 1. A steady stagnation-point flow is assumed to be maintained by photospheric convection:

$$\begin{equation} {\bf v} = \alpha (-x, \kappa y, (1-\kappa) z). \end{equation} \tag{ 5 }$$

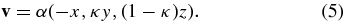
The solution describes a plasma flow that approaches the merging plane x = 0 along the x-axis, with streamlines that generally fan out in the yz-plane. The dimensionless parameter α>0 is the inflow speed normalized by the Alfvén speed. The flow is two-dimensional in the limiting cases κ = 0 and κ = 1. The streamlines are simply xz= const if κ = 0 and xy= const if κ = 1. In an intermediate case κ = 1/2, the flow fans out in the yz-plane so that xy² = c₁ and xz² = c₂. Analytical tractability is achieved by assuming that the local magnetic field depends on one spatial variable:

$$\begin{equation} {\bf B} (x, t) = (0, B_y (x, t), B_z (x, t)). \end{equation} \tag{ 6 }$$

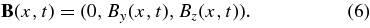
This should be a reasonable assumption because the stagnation flow will tend to align a general magnetic field along the plane x = 0. The observed cancellation corresponds to the merging of the oppositely directed z-components of the photospheric magnetic field.

Zoom In Zoom Out Reset image size

The goal of the calculation presented in the paper is to describe the main stages in the evolution of the magnetic field in a filament channel rather than to provide a detailed interpretation of the observed filament dynamics. In particular, the detailed mechanism by which photospheric convection drives the flow in the vicinity of a photospheric reconnection site is not addressed. The assumed stagnation-point flow has been repeatedly used to model plasma flows in the photosphere and is believed to provide a reasonable model for a local velocity field (e.g., Parker 1963; Clark 1965). Consistent with the assumed stagnation-point velocity, both upflows (e.g., Bellot Rubio & Beck 2005) and downflows (e.g., Chae et al. 2004) are observed to be associated with photospheric cancellation.

The scale on which the assumed stagnation-point flow can be expected to approximate the actual flow in the vicinity of a photospheric reconnection site is determined by the following considerations. On the one hand, the idealized stagnation-point flow is expected to be a valid approximation to the actual flows on scales that are small compared with the granular scale of the order of 1000 km. On the other hand, the flow is probably somewhat distorted by the reconnecting current sheet itself. The distortion, however, can only become significant on a length scale comparable to the sheet thickness. The thickness in a resistive Sweet–Parker model is at most a few kilometers (e.g., Litvinenko et al. 2007). The resulting reference length L of a few hundred kilometers is consistent with the above-given argument that the vertical extent of the sheet should not significantly exceed the atmospheric pressure scale height.

The assumed forms for v and B identically satisfy the divergence-free conditions above. The problem to be considered, therefore, consists in solving the momentum and induction equations that specify the evolution of the magnetic field, subject to a given initial condition

$$\begin{equation} {\bf B}_0 (x) = {\bf B} (x, 0). \end{equation} \tag{ 7 }$$

In what follows, the axial magnetic field in the filament channel, B_||(t), is identified with the magnetic field at the origin:

$$\begin{equation} B_\Vert (t) = B_y (0, t). \end{equation} \tag{ 8 }$$

Analytical solutions for planar magnetic merging (κ = 0, B_y = 0 in the present notation) and for the evolution of a nonreconnecting one-dimensional magnetic field in a two-dimensional stagnation-point flow (κ = 1, B_z = 0 in the present notation) are well known (Clark 1964, 1965). Steady solutions for the reconnecting and nonreconnecting magnetic field components had also been described (e.g., Fabling & Craig 1996). This paper considers a general case of the axial magnetic field evolution in the presence of a merging magnetic field component and a three-dimensional stagnation-point flow. Motivated by implications of the observational results of Wang & Muglach (2007) for solar filament channels, a new relationship between the maximum axial field and the speed of plasma inflow is derived and applied to the observations.

Using the assumed forms for v and B, the momentum Equation (1) can be shown to be identically satisfied. Hence, the problem is reduced to solving the induction Equation (2) that takes the following coordinate form:

$$\begin{equation} \partial _t B_y = \alpha x \partial _x B_y + \alpha \kappa B_y + \eta \partial _{xx} B_y, \end{equation} \tag{ 9 }$$

$$\begin{equation} \partial _t B_z = \alpha x \partial _x B_z + \alpha (1 - \kappa) B_z + \eta \partial _{xx} B_z. \end{equation} \tag{ 10 }$$

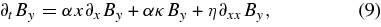
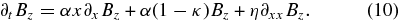
Here, the parameter κ must be in the range 0 ⩽ κ < 1 in order to describe the pile-up merging of B_z and upflow v_z>0 for z>0, which are associated with photospheric cancellation. Clearly, the equations allow B_y and B_z to be determined independently. As discussed above, it is the evolution of the nonreconnecting component B_y and in particular an expression for the axial field in the channel B_||(t) that are of primary interest.

A formal exact solution of the linear partial differential Equation (9) can be written down. Before doing this, however, it is instructive to analyze the ideal limit η = 0. In this limit, the exact time-dependent solution of the initial-value problem B_y(0, t) = B_y0(x) is as follows:

$$\begin{equation} B_y (x, t) = e^{\alpha \kappa t} \, B_{y0} (x e^{\alpha t}), \end{equation} \tag{ 11 }$$

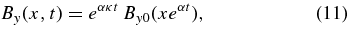
and therefore

$$\begin{equation} B_\Vert (t) = e^{\alpha \kappa t} \, B_\Vert (0). \end{equation} \tag{ 12 }$$

The last equation illustrates the key role of the flow dimensionality in the evolution of the axial field in the channel. The field increase can only occur in three-dimensional flows with κ>0. In the limit κ = 0, the inflow and outflow are exactly balanced, which leads to B_||(t) = B_||(0).

The increase of the axial magnetic field by ideal advection is eventually limited by resistive diffusion when the field gradient at x = 0 becomes large enough. Perhaps, the simplest method of deriving an exact solution to the general parabolic Equation (9) is by making a change of variables, which reduces it to the classical diffusion equation (e.g., Harper 1994). Specifically, the change of variables

$$\begin{equation} \xi = x e^{\alpha t}, \end{equation} \tag{ 13 }$$

$$\begin{equation} \tau = \frac{\eta }{2 \alpha } (e^{2 \alpha t} - 1) \end{equation} \tag{ 14 }$$

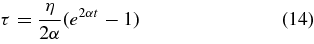
allows the solution B_y(x, t) to be represented in the form

$$\begin{equation} B_y (x, t) = e^{\alpha \kappa t} f (\xi, \tau), \end{equation} \tag{ 15 }$$

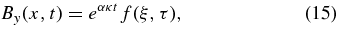
where

$$\begin{equation} \partial _{\tau } f = \partial _{\xi \xi } f. \end{equation} \tag{ 16 }$$

A similar formula for B_z(x, t) is obtained by the replacement κ → (1 − κ).

The general formula for B_y(x, t) follows from the solution to the initial-value problem:

$$\begin{equation} f (\xi, \tau) = \frac{1}{(4 \pi \tau)^{1/2}} \int _{-\infty }^{\infty } B_{y0} ({\tilde{\xi }}) \exp \left[ -\frac{(\xi - {\tilde{\xi }})^2}{4 \tau } \right] \, d {\tilde{\xi }}. \end{equation} \tag{ 17 }$$

Therefore, the axial magnetic field in the channel, B_||(t) = B_y(0, t), is given by

$$\begin{equation} B_\Vert (t) = \frac{e^{\alpha \kappa t}}{(4 \pi \tau)^{1/2}} \int _{-\infty }^{\infty } B_{y0} ({\tilde{\xi }}) \exp \left(-\frac{{\tilde{\xi }}^2}{4 \tau } \right) \, d {\tilde{\xi }}. \end{equation} \tag{ 18 }$$

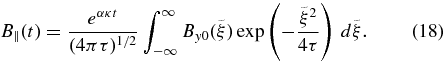
The properties of the solution are analyzed in the following section.

Because the merging magnetic field component B_z(x, t) changes its sign at x = 0, it is natural to model B_z by an odd function of x for sufficiently small x. Similarly, if the nonreconnecting axial field B_y(x, t) does not vanish at x = 0, an even function of x should give an accurate approximation to B_y for sufficiently small x. The formal solution above, however, does not depend on these assumptions.

In order to obtain concrete results, consider a Gaussian profile for the initial magnetic field:

$$\begin{equation} B_{y0} (x) = B_\Vert (0) \exp \left(-\frac{x^2}{2 \delta ^2} \right). \end{equation} \tag{ 19 }$$

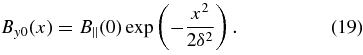
The model assumes that a nonzero axial component of the magnetic field is present initially, although no assumption is made concerning the magnitude of the field at t = 0. For a sufficiently small initial axial field B_||(0), a filament channel is not present initially. The Gaussian profile gives a mathematically convenient way to model a localized B_y0(x) that does not vanish at x = 0. By contrast, an initial axial field that is not localized at x = 0 seems unphysical. For instance, a uniform initial field would lead to an unlimited exponential growth of the axial field with time.

The integration in Equation (18) is performed to give

$$\begin{equation} \frac{B_\Vert (t)}{B_\Vert (0)} = e^{\alpha \kappa t} \left(1 + \frac{2 \tau }{\delta ^2} \right)^{-1/2}. \end{equation} \tag{ 20 }$$

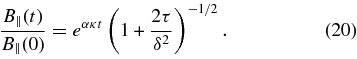
Now, using Equation (14) leads to the sought-after expression for the axial magnetic field in the filament channel:

$$\begin{equation} \frac{B_\Vert (t)}{B_\Vert (0)} = e^{\alpha \kappa t} \left[ 1 + \frac{\eta }{\alpha \delta ^2} (e^{2 \alpha t} - 1) \right]^{-1/2}. \end{equation} \tag{ 21 }$$

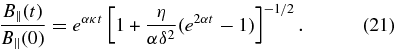
The time t_m at which the maximum value of B_||(t) is reached follows from the equation

$$\begin{equation} \left. \frac{d B_\Vert (t)}{dt} \right|_{t=t_m} = 0. \end{equation} \tag{ 22 }$$

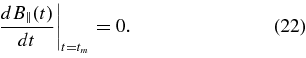
For the Gaussian initial profile, it follows that

$$\begin{equation} t_m = \frac{1}{2 \alpha } \ln \frac{(\alpha \delta ^2 / \eta - 1)}{(1/\kappa - 1)}, \end{equation} \tag{ 23 }$$

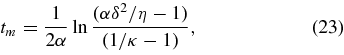
and the maximum axial field increase factor, b_m ≡ B_||(t_m)/B_||(0), is given by

$$\begin{equation} b_m = \kappa ^{\kappa /2} \left(1 - \kappa \right)^{(1 - \kappa)/2} \left(1 - \frac{\eta }{\alpha \delta ^2} \right)^{(\kappa - 1)/2} \left(\frac{\alpha \delta ^2}{\eta } \right)^{\kappa /2}. \end{equation} \tag{ 24 }$$

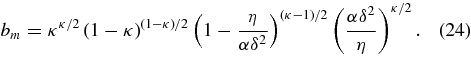
The model is physically meaningful only if t_m>0. This leads to the following constraint:

$$\begin{equation} \frac{\alpha \delta ^2}{\eta } > \frac{1}{\kappa }. \end{equation} \tag{ 25 }$$

Physically, this is simply a condition for B_||(t) to have a maximum at t_m>0. If the condition is not satisfied, resistive diffusion causes B_||(t) to decrease for all t>0. The roles of advection and diffusion are illustrated by the asymptotic forms of the solution for small and large times:

$$\begin{equation} \frac{B_\Vert (t)}{B_\Vert (0)} \approx 1 + \left(\alpha \kappa - \frac{\eta }{\delta ^2} \right) t, \quad t \ll t_m, \end{equation} \tag{ 26 }$$

$$\begin{equation} \frac{B_\Vert (t)}{B_\Vert (0)} \approx \left(\frac{\alpha \delta ^2}{\eta } \right)^{1/2} e^{\alpha (\kappa - 1) t}, \quad t \gg t_m. \end{equation} \tag{ 27 }$$

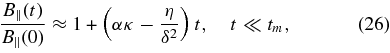
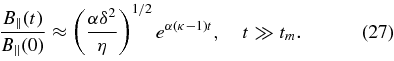
The asymptotic forms also illustrate the fact that field amplification can only happen in three-dimensional flows with κ>0, in agreement with the solution in the ideal limit η = 0.

As long as αδ²/η ≫ 1, Equation (24) implies that a faster inflow leads to a stronger axial magnetic field:

$$\begin{equation} b_m \sim \alpha ^{\kappa /2}. \end{equation} \tag{ 28 }$$

This is the main result of the analysis, which relates the maximum axial magnetic field in the channel to the reconnection rate and quantifies the observed correlation between the magnetic field in the channel and the rate of photospheric cancellation. The application of the formula to the solar data, however, can be complicated if the geometry of the flow, quantified by the parameter κ, varies significantly from event to event.

For completeness, note the behavior of the axial field in the limiting case κ = 1. In this case, the stagnation-point flow is strictly horizontal. Depending on its initial value, B_||(t) either decreases or increases monotonically and tends to a finite limit as t → ∞:

$$\begin{equation} \frac{B_\Vert (\infty)}{B_\Vert (0)} = \left(\frac{\alpha \delta ^2}{\eta } \right)^{1/2}. \end{equation} \tag{ 29 }$$

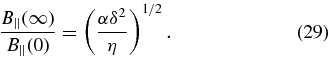
As an illustration, consider a typical photospheric canceling feature, characterized by the length scale L ≃ 10³ km, the inflow speed v_i ≃ 0.1 km s⁻¹, the Alfvén speed v_A ≃ 10 km s⁻¹, and the electric conductivity σ ≃ 10¹¹ s⁻¹ (e.g., Litvinenko et al. 2007). The corresponding dimensionless parameters of the problem are η ≃ 10⁻⁵ and α = v_i/v_A ≃ 10⁻². Although the geometry of photospheric reconnection is not known in sufficient detail, it seems reasonable to assume the values of δ ≃ 1 and κ = 1/2 for order-of-magnitude estimates.

For these reference values, αδ²/η ≃ 10³ ≫ 1 and Equation (25) is certainly satisfied. In the process of cancellation, the axial field increases by a factor of b_m ≃ 4. The increase should be observationally significant. For example, a maximum axial field of a few hundred Gauss could be reached given an initial field B₀ ≃ 100 G. It is only in the unlikely case of strictly horizontal flows (κ = 1) that the axial field might increase by a factor of about 30 for sufficiently long times. Alternatively, assuming that 0 < κ < 1 is uniformly distributed, an expected value of b_m can be estimated as

$$\begin{equation} \langle b_m \rangle = \int _0^1 b_m d \kappa \simeq \frac{(\alpha \delta ^2 / \eta)^{1/2}}{\ln (\alpha \delta ^2 / \eta)^{1/2}} \,, \end{equation} \tag{ 30 }$$

which leads to 〈b_m〉 ≃ 9 for the adopted values of the parameters. Thus, the maximum predicted field seems to remain below a kilo-Gauss upper limit imposed on the photospheric magnetic field by pressure balance considerations, although one should remember that the pressure-balance limit on the magnetic field decreases with height above the lower photospheric boundary (Stenflo 1989 and references therein).

Equation (23) gives an estimate for the time it takes for the axial field to reach the maximum strength (unless the filament erupts earlier). For the parameters above, t_m ≃ 350, which corresponds to about 10 hr, given the Alfvén time t_A ≃ 10² s. It is worth noting that a stronger localization of the initial field (δ < 1) would lead to stronger resistive diffusion, shorter time scales for the evolution of B_||(t), and smaller field increase factors.

The height at which reconnection occurs determines the density and electric resistivity of the plasma and hence the parameters of the reconnecting current sheet. Litvinenko et al. (2007) argued that the observed cancellation is most likely to correspond to reconnection in the temperature minimum region, yet there is no fundamental reason to exclude the possibility that reconnection takes place at smaller or larger heights (e.g., Litvinenko & Chae 2009), which would change the numerical estimates above. A larger electric resistivity η, for instance, would lead to a smaller increase factor b_m. Note, however, that the time t_m at which the maximum value of the axial magnetic field is reached depends only weakly (logarithmically) on the electric resistivity.

Photospheric cancellation and filament channel formation are thought to be principal processes in a sequence of events leading to eruptive solar phenomena that include erupting filaments and coronal mass ejections (Martin et al. 2008). A quantitative model for photospheric magnetic reconnection in the Sweet–Parker (Parker 1957) current sheet appears to give a satisfactory explanation for the observed cancellation rates (Litvinenko et al. 2007 and references therein; see, however, Cassak & Drake 2009 for an interesting alternative approach).

Motivated by recent observations of filament channels (Wang & Muglach 2007), this paper addresses a different aspect of photospheric cancellation. A quantitative model is presented, which relates the rate of photospheric magnetic reconnection and the maximum axial magnetic field in the filament channel. The complete time-dependent solution for the axial field B_||(t) describes its initial advective growth in a three-dimensional stagnation-point flow, followed by resistive decay. While the stagnation-point flow is well known to admit a class of exact MHD solutions for the merging of planar magnetic fields (Clark 1964, 1965; Fabling & Craig 1996), both the specific magnetic geometry, analyzed in this paper, and the application of the model to the observed properties of filament channels appear to be new.

The derived relationship (Equation (24)) between the dimensionless reconnection inflow speed α and the maximum axial field increase factor, b_m ≡ B_||(t_m)/B_||(0), quantifies the correlation between the rate of filament channel formation and the strength of the axial magnetic field. It is worth stressing that physically, a faster rate of photospheric magnetic reconnection leads to a stronger axial field in the channel. Hence, the field increase factor b_m is an indicator of the reconnection rate. Of course, a stronger initial axial magnetic field by itself could cause the alignment of the vector magnetic field with the chromospheric fibrils and a polarity inversion line, thus defining a filament channel. It is magnetic reconnection, however, that is ultimately responsible for the transfer of mass and magnetic flux through the polarity inversion line to the chromosphere and corona, building up filament channels and filaments and eventually leading to solar eruptive events, probably triggered by some additional mechanism.

The direction of the magnetic field in the channel is thought to be determined by the initial helicity of the interacting magnetic bipoles and their initial tilt angles (Mackay & van Ballegooijen 2005). Flux emergence or photospheric differential rotation in the time interval between flux emergence and cancellation determines the magnitude of the axial magnetic field in the channel at the start of cancellation. The evolution of the field in the channel in the course of cancellation, however, does not seem to have been described theoretically until now.

Notably, the same effect of enhancement of the axial magnetic field due to its transport by reconnection plasma flows has been directly observed in the course of current sheet formation in a recent laboratory experiment (Frank et al. 2009). One might speculate that side-by-side analysis of the experimental and solar data could lead to progress in understanding the dynamics of three-dimensional magnetic reconnection in different parameter regimes.

Useful discussions with I. J. D. Craig, S. F. Martin, and O. Panasenco, as well as a detailed constructive report by the anonymous referee, are gratefully acknowledged. This work was supported by NASA grant NNX08AG44G, NSF grants ATM-0734032 and ATM-0837915, and by a research fellowship from the Alexander von Humboldt Foundation.