Substellar Companion Masses from Minimal Radial Velocity or Astrometric Information: a Monte Carlo Approach

The recent discovery of candidate low‐mass companions around nearby stars by several teams using Doppler techniques (Latham et al. 1989; Mayor & Queloz 1995; Marcy & Butler 1996; Cochran et al. 1997; Noyes et al. 1997) has opened an exciting new field in astronomy that was hardly mentioned 10 years ago: that of extrasolar planets, with masses under about 10 times the mass of Jupiter. The harvest of substellar candidates from the radial‐velocity searches includes also several objects (e.g., Mayor, Queloz, & Udry 1998) that are probably too large to be called planets but could turn out to be equally interesting brown dwarfs, failed stars with masses under about 80 times that of Jupiter. Astrometric searches for planets from perturbations induced on the primary star are also underway (e.g., Gatewood et al. 1997). The developments have been so rapid over the past few years that serious efforts are now being made toward the direct detection (imaging) of such faint objects using adaptive optics (see Sandler 1997; Olivier et al. 1998), which may well succeed in the near future. Even spectroscopy of these extremely faint sources is being discussed (e.g., Angel & Woolf 1997).

The unexpected properties of some of these low‐mass candidates found to date through indirect methods have already been the subject of a number of theoretical studies providing new insight into the origin and evolution of our own solar system. However, the true measure of a planet—its mass—remains unfortunately undetermined in the radial velocity technique, the most successful of the detection methods applied so far. Doppler studies can only provide a lower limit to the mass of the companion, M_B, because the inclination angle i of the orbit is typically unknown:

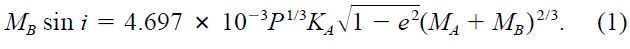
The observables in this expression are the orbital period P (expressed in days), the velocity semiamplitude K_A of the primary star (in kilometers per second), and the eccentricity e. The companion mass M_B is in units of the solar mass. An estimate of the primary mass M_A is also required but is usually not difficult to obtain, if only from the spectral type.

Various arguments can be made—and have been made in a number of cases—to place useful upper limits on the mass of these companions. For example, one may consider the rotational broadening of the spectral lines of the primary, vsin i, together with independent estimates of the radius and the rotational period of the star, if available, to obtain a rough estimate of the inclination angle (but see limitations discussed by Soderblom 1985). The underlying assumption here is that the orbital and rotational axes are aligned. Alternatively, if the orbit is circular and the period short enough, one may attempt to determine through suitable activity indicators whether or not the rotation of the primary is locked in synchronism with the orbit and argue from this whether the companion is large enough to induce the necessary tidal effects given the age of the system (see also Drake et al. 1998). Nevertheless, the fact remains that the true mass of these Doppler companions cannot be determined solely from spectroscopy.

If the orbit happens to be close enough to edge‐on, the transit of the companion in front of the central star may produce a detectable drop in the brightness of the system, which would allow very tight limits to be placed on the inclination angle and therefore on the mass. Photometric planet searches of this kind are being actively pursued, particularly in close eclipsing binary systems such as CM Dra, where the likelihood of detection is expected to be enhanced if the planets tend to share the orbital plane of the binary (see, e.g., Deeg et al. 1998; Doyle et al. 1998).

The direct detection of a companion having a known spectroscopic orbit would also solve the problem, since two measurements of the angular separation at different orbital phases are then sufficient to determine the inclination angle along with the semimajor axis of the relative orbit (see eq. [5] below). With an estimate of the mass for the primary, equation (1) then gives the mass of the companion directly. If the distance is known independently, then no estimate of M_A is necessary and both masses follow from Kepler's Third Law and equation (1).

Direct imaging of very faint substellar companions at close separations from their bright primary stars is still probably a few years away, but great progress is being made in that field. Planned instruments on space platforms (coronographs, nulling interferometers) are expected to be able to detect these objects at angular separations as close as a few tenths of an arcsecond from the parent star. The information provided by these detections will be crucial for our understanding of these objects.

For stars at distances of 10 to 30 pc from the Sun, usually targeted in the past for this type of search, angular separations of a few tenths of an arcsecond imply orbital periods of a decade or more, typically longer than the duration of the space missions on which these new instruments will fly. Such periods are also long for ground‐based Doppler studies. Thus, it seems unlikely that radial‐velocity surveys will be able to provide a complete orbital solution for newly imaged planetary candidates with periods of a few decades. At most, small long‐term velocity trends will be measured, as they have been already for a number of interesting candidates.

A similar prospect holds for the ground‐based astrometric detections. New space missions are planned that will increase by several orders of magnitude our ability to detect the reflex motion of a star in the plane of the sky caused by orbiting planets. Some of these planets may have periods short enough that their orbits can be covered in the duration of the mission (typically a few years), but many will likely not.

For the cases where simple accelerations are detected from Doppler or astrometric studies, it is still possible to gain some knowledge of the mass of the companion from a statistical point of view if the angular separation can eventually be measured. In this paper we explore this possibility through a Monte Carlo approach, and derive the corresponding probability distributions of the secondary mass separately for the spectroscopic case and the astrometric case. We then apply the method to a few real examples and derive expected secondary masses for a range of hypothetical angular separations, if these objects were to be imaged directly.

A companion in orbit around its parent star will exert on it a pull, the line‐of‐sight component of which can be measured directly by the Doppler technique if it is large enough. The general expression for the measured radial velocity of the primary star is

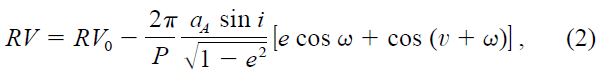
where ω is the longitude of periastron of the companion, v is the true anomaly, and RV₀ is the velocity of the center of mass of the system. The linear semimajor axis of the orbit of the primary star, a_A, is related to the linear semimajor axis of the relative orbit, a, by a_A = aM_B/(M_A + M_B).

We assume that a change in the radial velocity of the primary has been detected, but that the period is very long so that only an acceleration (a slope), d(RV)/dt, can be measured. By differentiation we obtain

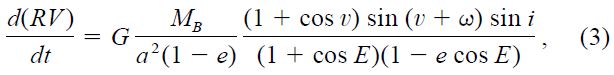
in which we have made use of Kepler's Third Law as well as Kepler's equation for elliptical motion. The eccentric anomaly E is related to the true anomaly by

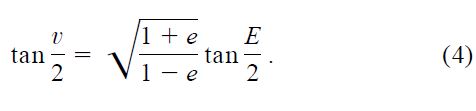
Direct imaging allows the measurement of the angular separation ρ between the companion and the parent star, which sets the angular scale of the relative orbit:

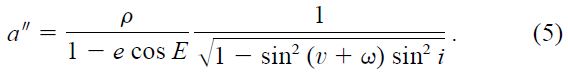
We will further assume that an estimate of the distance D to the primary star is available, either by direct measurement (trigonometric parallax) or inferred from its spectral type, so that a^'' may be converted to a linear semimajor axis, a.

Substituting equation (5) into equation (3) we have an expression for the secondary mass in terms of the measured angular separation, the measured radial acceleration, and the distance estimate:

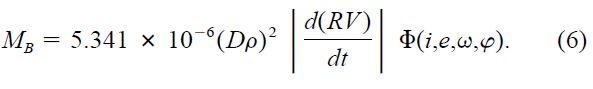
Φ is a function of the inclination angle, the eccentricity, the longitude of periastron, and the phase in the orbit, φ, all of which are unknown, in principle. It is given by

The phase is implicit in the true anomaly v and in the eccentric anomaly E through equation (4) and Kepler's equation,

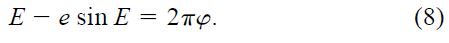
The numerical constant in equation (6) is such that the companion mass comes out in solar units when the acceleration is measured in meters per second per year, the angular separation in arcseconds, and the distance in parsecs.

We note that the companion mass as expressed by equation (6) does not depend explicitly on the mass of the primary, so no estimate of M_A is necessary, as it is in equation (1). The primary mass is of course implicit in d(RV)/dt, which is measured directly. Also, the application of equation (6) is not restricted to substellar companions, since no assumption is made on the mass or brightness of the object in orbit around the primary star.

To illustrate the use of equation (6) we apply it first to the case of Procyon, a classical visual binary that has a well‐determined astrometric orbit with a period of 40 years. The primary has been monitored by several groups employing Doppler techniques with a precision similar to those that led to the recent planet discoveries. Irwin et al. (1992) presented precise radial velocity measures that they used to rediscuss the orbit of Procyon and derive the mass of the white dwarf secondary. These velocities were conveniently obtained on the linear part of the velocity curve. We computed the slope from these data (d(RV)/dt = + 129.86 m s⁻¹ yr⁻¹) and used the orbital elements to calculate the angular separation, ρ = 5202, at the mean epoch of the velocity observations (1985.69). For the parallax we adopted the value measured by Hipparcos (ESA 1997), which corresponds to a distance of 3.50 pc.

We now take these three quantities (d(RV)/dt, ρ, and D) as the observables, and ignore the orbital elements since those will not be known in actual applications of the scheme developed here. To gain information on the secondary mass we follow a numerical approach in which we adopt reasonable distributions for the inclination angle, the eccentricity, the longitude of periastron, and the phase, and we determine the probability density function (PDF) of companion masses from equation (6) with Monte Carlo simulations.

For i we adopt P(i)di = sin i di, which corresponds to random orientation of the orbital planes. For the eccentricity we use in this example P(e)de = 2e de, which is frequently adopted for visual binaries, and for which there is some theoretical (Ambartsumian 1937) and observational support (Duquennoy & Mayor 1991; Tokovinin 1998). Circular orbits are presumably a better assumption for the case of planetary companions, which are formed differently than stars, but we find that the results are insensitive to the choice of P(e). The longitude of periastron and the phase in the orbit may be assumed to have a uniform distribution.

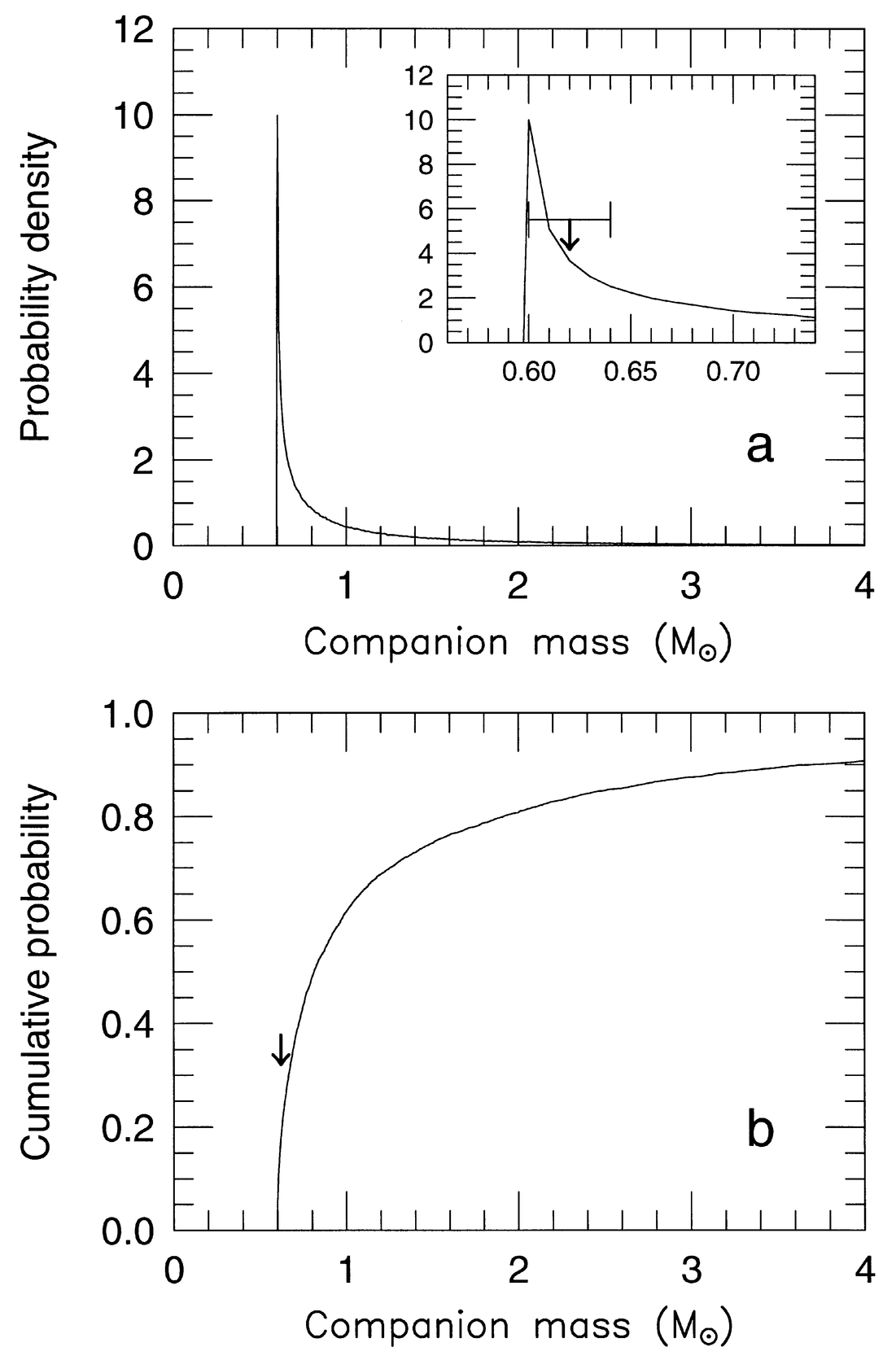
Figure 1a shows the probability distribution we obtain for the secondary mass of Procyon. It has a very sharp peak toward the left, which is in fact a singularity, and a long tail toward larger masses that corresponds to the fact that one cannot rule out very large masses due to unlikely orientations of the orbit.¹ The actual mass determined by Irwin et al. (1992) is M_B = 0.62 ± 0.02 M_⊙, which is indicated with an arrow in the insert.

Zoom In Zoom Out Reset image size

From distributions such as this it is possible to make quantitative statements in a given individual case about the likelihood of a candidate having a mass smaller than a certain value even from minimal Doppler and astrometric information, as in this example. This is most conveniently done by computing the cumulative probability distribution (CDF), shown in Figure 1b. For Procyon the curve indicates roughly a 60% probability that M_B is less than 1 M_⊙, and a 75% chance that it is smaller than 1.5 M_⊙.

The astrometric detection of a "wobble" or acceleration in the motion of a star in the plane of the sky is considerably more difficult than the detection of a radial acceleration by the Doppler technique, which explains why the astrometric method has been less successful in finding potential low‐mass companions. The astrometric wobble is a second‐order perturbation of the observable (the position), while the radial acceleration is a first‐order effect, since in that case the observable (the radial velocity) is already a first derivative. The astrometrist's task is made even more difficult by the fact that the signal searched for is a residual effect that is apparent only after taking out the much larger contributions from the proper motion and the parallactic motion, which must generally be determined from the same set of observations. It takes time to detect curvature in the residuals, a simple linear trend being usually indistinguishable because it is absorbed into the proper motion terms. Nevertheless, the technique is valuable and complementary to the spectroscopic method, and many well‐known examples of unseen stellar companions found in this way leave little doubt of its potential for finding Jupiter‐class planets, especially with the improvements in accuracy of ground‐based efforts in recent years, and those expected in future space missions.

As in the case considered before of a spectroscopically measured acceleration in the radial direction, a similar formalism can be developed for situations where an astrometric perturbation has been detected from the ground or from space. A single measurement of the angular separation then allows valuable statistical information to be derived on the mass of the companion.

Following the classic notation (e.g., van de Kamp 1967), the measured position relative to faint background stars of a target star that shows a perturbation by an unseen companion may be expressed in general form as

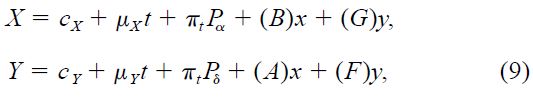
where the first term on the right in each equation represents the heliocentric position of the primary at a fiducial epoch, μ_X and μ_Y are the annual proper motions, π_t is the annual trigonometric parallax, and P_α and P_δ are the parallax factors in right ascension and declination. The symbols (B), (G), (A), and (F) are the so‐called "geometric" elements, analogous to the Thiele‐Innes constants but referring to the photocentric orbit. We assume, as usual, that the X and Y axes are aligned with right ascension and declination, respectively. The quantities x and y are the elliptical rectangular coordinates in the unit orbit, given by

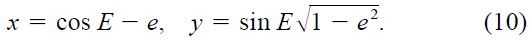
The Thiele‐Innes constants for the photocentric orbit are given in terms of the orientation elements as

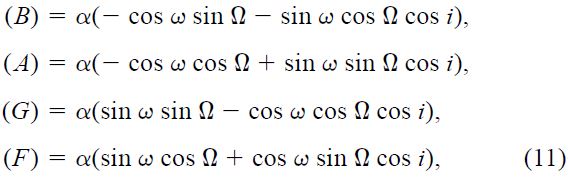
where α is the semimajor axis of the photocentric orbit, in arcseconds. In the case under consideration—astrometric studies where the reflex motion of the primary is measurable but the light of the companion is undetectable—α is simply the semimajor axis of the primary orbit, α = a^''M_B/(M_A + M_B). The angle Ω is the position angle of the ascending node of the orbit.

We assume now that the proper motion and parallactic motion of the primary have been sufficiently well determined so that they can be taken out, and we are left with the perturbation terms

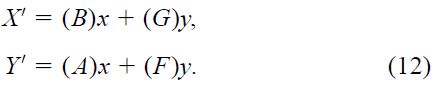
Curvature in these residuals over time (acceleration) indicates the presence of a companion. In practice, the acceleration (second derivatives of X^' and Y^') could be measured by fitting a parabola to the residuals and considering the second order coefficients in R.A. and declination. Differentiating equation (12) leads to

where, from Kepler's equation we have

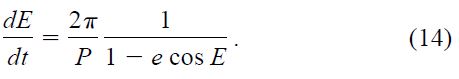
The quantities d²X^'/dt² and d²Y^'/dt² represent the observable accelerations and are assumed in the following to be measured in units of arcsec yr⁻².

Combining the two equations in (13) with equation (5) above, and using Kepler's Third Law, we obtain

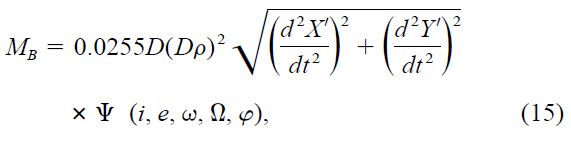
where again we have assumed that an estimate of the distance is available. The function Ψ depends only on the shape and orientation of the orbit of the companion, and on the phase φ. It is given by

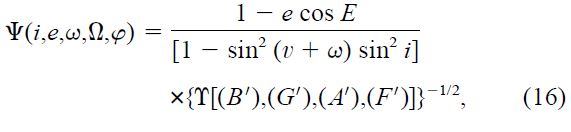
where the auxiliary quantity ϒ is defined in terms of modified Thiele‐Innes constants [(B^'), (G^'), (A^'), (F^')] that differ from their classical expressions in equation (11) only in that they do not contain the common factor α:

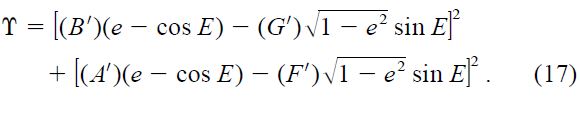
Equation (15) is the astrometric equivalent of equation (6), obtained for the spectroscopic case. It may be used in the same way to generate a probability distribution for the companion mass, given the observables d²X^'/dt² and d²Y^'/dt², the angular separation ρ, and an estimate of the distance D. To illustrate this with an example we return to Procyon, whose white dwarf companion was in fact discovered in the last century through perturbations in the motion of the primary on the plane of the sky. Using the orbital elements published by Irwin et al. (1992), we compute the values d²X^'/dt² = -00479 yr⁻² and d²Y^'/dt² = -00930 yr⁻², along with the angular separation ρ = 4488, at an arbitrary epoch 2000.0. We then use these three quantities as observables, together with the known distance to the star (3.50 pc).

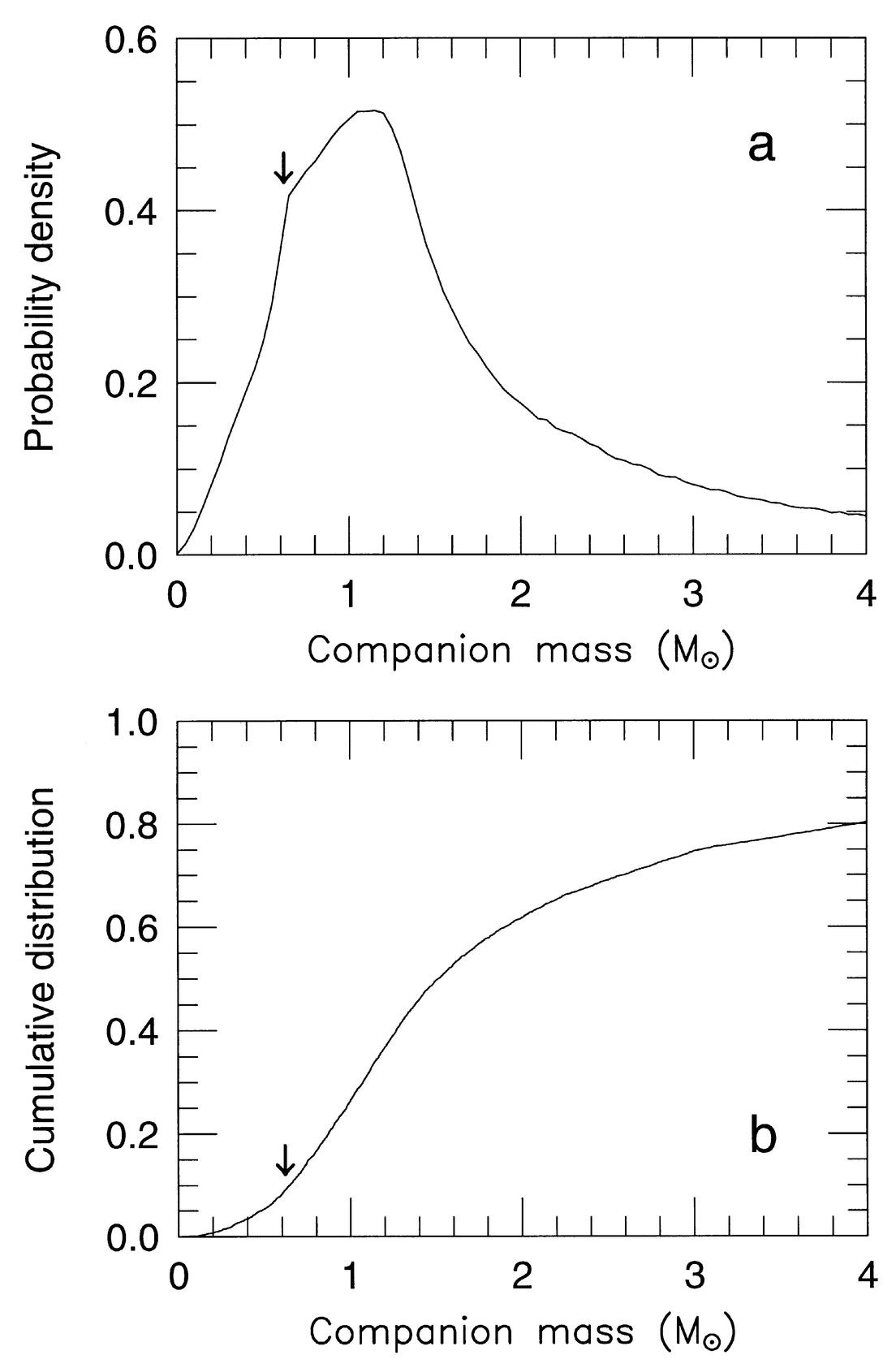
Once again we use a Monte Carlo approach to construct the probability distribution function of companion masses, with input distributions for i, e, ω, and φ as in the previous section, and a uniform distribution for Ω. The result is shown in Figure 2a. It is considerably broader than the distribution obtained in the spectroscopic case. The true mass of the secondary of Procyon as derived by Irwin et al. (1992) is indicated in the figure. The probability that the companion mass is smaller than a given value in this example is described by the cumulative distribution function shown in Figure 2b. In this case the simulations indicate that there is only a 25% chance that the companion is smaller than 1 M_⊙ and roughly a 50% probability that it is smaller than 1.5 M_⊙.

Zoom In Zoom Out Reset image size

From the shape of the distributions in Figures 1a and 2a, the former being much narrower than the latter, it is clear that the detection of an acceleration in the radial direction constrains the companion masses much more than the measurement of an astrometric acceleration, once the angular separation has been measured. The only reason the sharp peak in Figure 1a does not go to infinity is because of the limited number of simulations used to construct the distribution (10⁶ in this illustration) and the nonzero bin width for the plot. We note also that the probability distribution for the radial velocity case has a lower limit that is larger than zero, unlike the astrometric case (for the particular eccentricity distribution adopted in the example of Procyon). The minimum of Φ(i, e, ω, φ) is 3√3/2, which can be easily derived analytically for the case e = 0 and shown to be true for any eccentricity by numerical simulations. In the astrometric case, the minimum of Ψ(i, e, ω, Ω, φ) can be zero or larger than zero, depending on P(e).

The probability statements based on the CDF, such as those in the previous sections for the example of Procyon, assume that the companion mass is completely unconstrained by any observations other than those used to compute the distribution. In practice, however, there is always an upper limit to the mass, M^lim_B, that can be set from various physical arguments. The actual PDF is therefore truncated at M^lim_B. Since the CDF is the integral of the PDF, the CDF should in principle reach unity for a mass equal to this upper limit.

Consequently, in real applications of this method, the probability distributions for both the radial velocity case and the astrometric case should be renormalized so that their integral up to M^lim_B is unity. This will change the CDFs, and tend to increase the probability that the companion mass is smaller than any given value. The magnitude of the change will depend on how stringent the upper limit on the mass of the companion is. For example, if we assume, returning to the example of Procyon, that its companion is smaller than the primary (M^lim_B ≈ 1.7 M_⊙), then the probability estimates for the astrometric case based on the CDF in Figure 2b are modified significantly. The probability that M_B is lower than 1 M_⊙ is now ∼50% (as opposed to 25%), and the chance that it is smaller than 1.5 M_⊙ is 90% (50%). The effect may not be as large in the case of low‐mass companions if the upper limits are not as tight.

Several examples have been identified already in the literature in which very small long‐term trends in the radial velocity of the target star have been measured, suggesting the companions are possibly substellar. The direct detection of these companions through imaging would allow the application of equation (6) as described above. Although such detections have yet to be made, Table 1 gives the most likely mass for the companions that would be inferred, as a function of the angular separation.

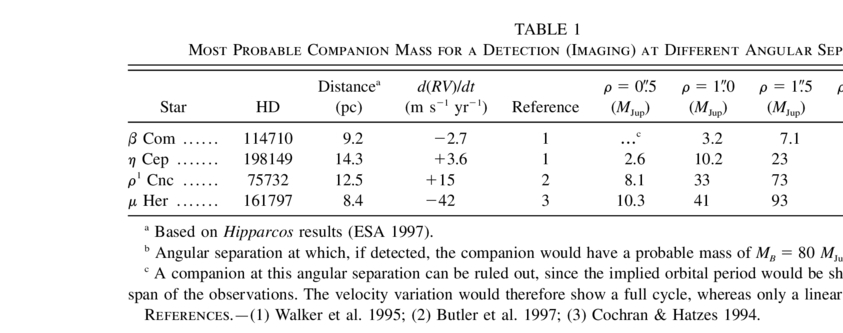In one or two of these cases (β Com, η Cep) there are suggestions in the literature indicating that the observed velocity variations could be due to the magnetic activity cycles in these stars, instead of a companion in orbit (see Nelson & Angel 1998), but this has not yet been confirmed and will require continued monitoring of both the radial velocity and chromospheric activity indicators such as the Ca ii H and K S‐index. In the case of ρ¹ Cnc (Butler et al. 1997), the radial velocity variation considered is actually the residual motion after accounting for a closer companion with a period of 14.6 days. As reported by Butler et al., the long‐term upward trend shows signs of leveling off in the last few years of observation, i.e., shows curvature. For the purpose of this illustration we have computed the slope using only the linear portion of that trend (1989–1994 interval).

The last column in Table 1 shows the angular separation at which the most likely mass would be 80 M_Jup, the dividing line between stars and brown dwarfs. All of these candidates would have probable masses that are substellar if detected at separations smaller than about 14.

Closer companions for which the full orbits have been determined spectroscopically are already being used in the discussion of fundamental astrophysical issues such as the formation and evolution of extrasolar planets and brown dwarfs. Although their numbers are still small, statistical methods have been applied in order to infer their true mass distribution (e.g., Mazeh, Goldberg, & Latham 1998). Because we know so little about these objects, it is very important that the full range of separations be sampled to avoid possible biases. Thus, wider companions detected only through accelerations ought to be included in the statistical analyses as well, when it becomes possible to image them. In addition to the statistical information contained on the masses, a direct detection provides another estimate of the mass from the brightness of the object, albeit age and model dependent.

To conclude, we mention here that a single measurement of the angular separation of a companion from the primary star does not give the true size of the relative orbit because it is only a projection, although ρ and a^'' are frequently considered to be the same for simplicity. This is only true for circular orbits viewed face‐on. Occasionally, a simple statistical relation between the two is adopted, for example, log a^'' = 0.146 + log ρ (Poveda et al. 1994), or other similar expressions. There is indeed information about a^'' contained in ρ, but only in the form of a probability distribution if the other orbital elements are not known. This can be seen easily from equation (5).

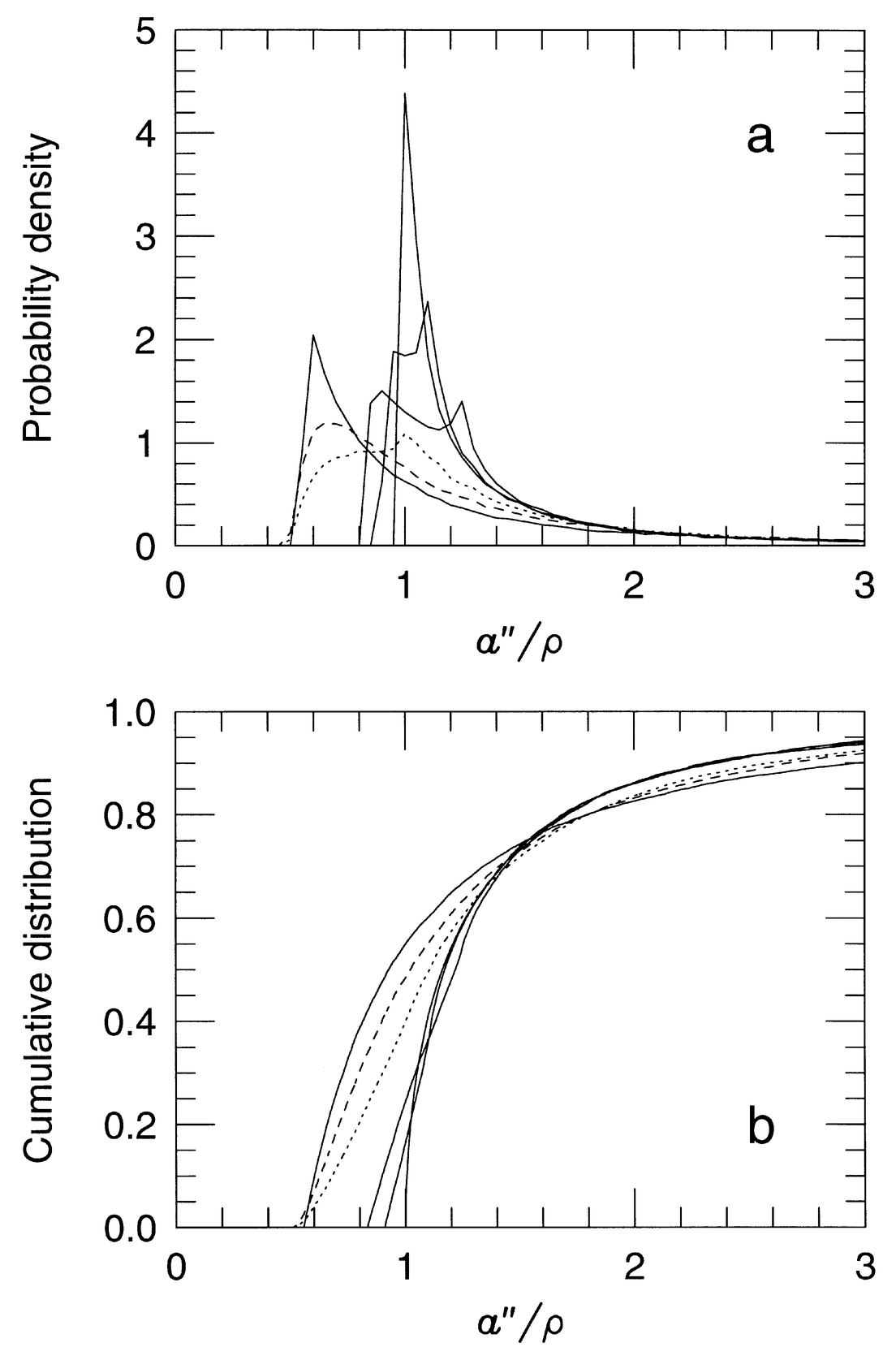
By Monte Carlo simulations one can compute this distribution for any adopted eccentricity, or distribution of eccentricities, in much the same way as we have done above for the masses. Figure 3a displays the probability distribution of a^''/ρ, from which that of the linear semimajor axis a (e.g., in AU) can be derived if the distance to the star is known. Several curves are shown for different assumptions on the eccentricity distribution P(e). The semimajor axis can be smaller or much larger than the angular separation. For the case of circular orbits the peak occurs at 1.0, but for other eccentricity distributions it is shifted, or there are two peaks. The corresponding cumulative distributions are shown in Figure 3b. If an estimate of the primary mass is available, the probability distribution of the orbital period follows directly from that of a and Kepler's Third Law.

Zoom In Zoom Out Reset image size

In light of the recent advances in the detection of very faint astronomical sources, the direct imaging of substellar companions to nearby stars is likely to become a reality in the near future. For cases where accelerations induced on the primary star can also be measured (in the radial direction or in the plane of the sky), an important constraint is provided by a single measurement of the angular separation that allows valuable statistical information on the mass of the companion to be obtained. We have derived analytical expressions for the mass in terms of those observations and the orbital elements, both for the spectroscopic case and the astrometric case. Using these expressions, the probability distribution of companion masses can be generated easily with Monte Carlo simulations. This statistical information is an important complement to that obtained for closer substellar companions, which is already being used to infer the mass distribution of the known population of substellar objects.

We show also that the angular semimajor axis a^'' can be quite different from the measured angular separation ρ, depending on the eccentricity, and we use the same technique as above to derive the corresponding probability distribution.