Abstract
The purpose of these notes is to provide a systematic quantitative framework – in what is intended to be a ‘pedagogical’ fashion – for discussing mean-reversion and optimization. We start with pair trading and add complexity by following the sequence ‘mean-reversion via demeaning → regression → weighted regression → (constrained) optimization → factor models’. We discuss in detail how to do mean-reversion based on this approach, including common pitfalls encountered in practical applications, such as the difference between maximizing the Sharpe ratio and minimizing an objective function when trading costs are included. We also discuss explicit algorithms for optimization with linear costs, constraints and bounds. We also illustrate our discussion on an explicit intraday mean-reversion alpha.


Similar content being viewed by others
Notes
1 ‘Mean-reversion strategy’ is mostly trader lingo – which is what the author is accustomed to. Academic finance literature mostly uses ‘contrarian investment strategy’ instead. This article uses the term ‘mean-reversion (strategy)’ throughout.
2 ‘Specific risk’ is multi-factor risk model terminology. Some may prefer ‘idiosyncratic risk’.
3 For a partial list of references on mean-reversion, optimization and related topics, see, e.g., Adcock and Meade (1994); Allaj (2013); Atkinson et al (1997); Avellaneda and Lee (2010); Best and Hlouskova (2003); Black and Litterman (1991); Black and Litterman (1992); Cadenillas and Pliska (1999); Cheung (2010); Chu et al (2011); Cvitanić and Karatzas (1996); Daniel (2001); Da Silva et al (2009); Davis and Norman (1990); Drobetz (2001); Dumas and Luciano (1991); Fama and French (1993); Fama and MacBeth (1973); Gatev et al (2006); He and Litterman (1999); Hodges and Carverhill (1993); Idzorek (2007); Janeček and Shreve (2004); Jegadeesh and Titman (1993); Jegadeesh and Titman (1995); Knight and Satchell (2010); Liew and Roberts (2013); Lo and MacKinlay (1990); Magill and Constantinides (1976); Markowitz (1952); Merton (1969); Mitchell and Braun (2013); Mokkhavesa and Atkinson (2002); O’Tool (2013); Perold (1984); Poterba and Summers (1988); Rockafellar and Uryasev (2000); Satchell and Scowcroft (2000); Sharpe (1966) and Shreve and Soner (1994), and references therein.
4 Here and in the following
 refers to the cross-sectional mean return (not the time series mean return). Also,
refers to the cross-sectional mean return (not the time series mean return). Also,  ,
, 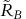 and
and  (see below) refer to the deviation from the mean return
(see below) refer to the deviation from the mean return 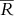 .
.5 We assume no leverage and 0 margins. Nontrivial leverage simply rescales the investment level I. If margins are present, on top of I invested in stocks, we need an additional amount I′ to maintain margins, which simply reduces the strategy return due to the borrowing interest rate.
6 For example, we could have one group of stocks from the oil sector, the second group from technology, and the third group from, say, health care.
7 The R Package for Statistical Computing. Also, ‘~’ in (22) is R notation for a linear model.
8 We will discuss these subtleties below, when we discuss factor models and optimization.
9 As we discuss in the next section, this case is a certain limit of optimization.
Be it owing to changes from one day to another, or due to computational uncertainties and so on.
In this case, the actual portfolio consists of net long or short positions for individual stocks arising from long positions D i and short positions from the minimum variance portfolio.
Above we considered homogeneous constraints (66). Technically, the same trick can be applied to inhomogeneous constraints of the form Σ i=1 N w i Y ia +y a =0. Everything goes through as above, except that now we have ρ a =−λy a . However, while this will give the correct solution to the minimization of the objective function, this is no longer necessarily the same as maximizing the Sharpe ratio with constraints: the latter explicitly break the invariance under the rescalings w i →ζw i (unless y a ≡0), which is what allowed us to rewrite the Sharpe ratio maximization problem in terms of the objective function minimization problem, whereby λ is fixed via (55). In the presence of inhomogeneous constraints this is no longer the case and some additional care is needed – see the section ‘Optimization with costs’. We will not need inhomogeneous constraints here, however.
More precisely, usually one would use the unrotated factor loadings
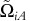 – recall that
– recall that  where
where  is the Cholesky decomposition of the factor covariance matrix Φ. However, a rotation Y→YU by an arbitrary nonsingular m × m matrix U
ab
does not change the constraints (66).
is the Cholesky decomposition of the factor covariance matrix Φ. However, a rotation Y→YU by an arbitrary nonsingular m × m matrix U
ab
does not change the constraints (66).For ρ=±1, the Sharpe ratio goes to infinity if R A ≠±R B : the volatility vanishes for
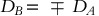 (recall that σ
A
=σ
B
). If R
A
=±R
B
, then the two instruments A and – long for plus sign and short for minus sign – B are indistinguishable for optimization purposes.
(recall that σ
A
=σ
B
). If R
A
=±R
B
, then the two instruments A and – long for plus sign and short for minus sign – B are indistinguishable for optimization purposes.For the sake of simplicity, the transaction costs for buys and sells are assumed to be the same.
Actually, w i derivatives are defined only for w i ≠0 and, for example, in the case of linear costs for w i ≠w* i – see the subsection ‘Optimization: general case’ for details.
For any λ″>0, there is a unique optimum assuming C ij is positive-definite, and all L i ⩾0.
We will discuss bounds below. Alternatively, one can squash returns to achieve the same.
This argument also goes through for partially establishing and liquidating trades with ξ⪅1, that is, ξ≡Σ i=1 N|w* i | need not be equal 1. Uniformity of L i can also be relaxed (with some care).
Note that stocks rarely jump (sub-)industries/sectors, and thus
 can be assumed to be static.
can be assumed to be static.More precisely, the intercept is already subsumed in Λ iA :Λ iA =1 if the stock labeled by i belongs to the cluster labeled by A=1, …, K; otherwise, Λ iA =0. Each stock belongs to one and only one cluster. This implies that Σ A=1 KΛ iA =1 for each i, thus a linear combination of the columns of Λ iA is the intercept.
This is a so-called ‘delay-0’ alpha – P is O is used in the alpha, and as the establishing fill price.
That is, to ensure that our results are not a mere consequence of the universe selection.
Note that, as the alpha is purely intraday, this ‘rebalancing’ does not generate additional trades, it simply changes the universe that is traded for the next 21 days.
The number of such tickers in our data is 3811. The number of BICS sectors is 10. The numbers of BICS industries is 48. The number of BICS sub-industries varies between 164 and 169 (due to small sub-industries, which are affected by the varying top-2000-by-ADDV universe).
Plus we are assuming ‘delay-0’, meaning, we can place the trades ‘infinitely’ fast right after receiving the opening prints from the exchange(s) and get filled at the very same open prices. And, as mentioned above, we are ignoring trading costs and slippage, hence the rosy ROC, SR and CPS.
References
Adcock, J.C. and Meade, N. (1994) A simple algorithm to incorporate transactions costs in quadratic optimization. European Journal of Operational Research 79 (1): 85–94.
Allaj, E. (2013) The Black-Litterman model: A consistent estimation of the parameter tau. Financial Markets and Portfolio Management 27 (2): 217–251.
Atkinson, C., Pliska, S.R. and Wilmott, P. (1997) Portfolio management with transaction costs. Proceedings of the Royal Society of London A 453 (1958): 551–562.
Avellaneda, M. and Lee, J.H. (2010) Statistical arbitrage in the U.S. equity market. Quantitative Finance 10 (7): 761–782.
Best, M.J. and Hlouskova, J. (2003) Portfolio selection and transactions costs. Computational Optimization and Applications 24 (1): 95–116.
Black, F. and Litterman, R. (1991) Asset allocation: Combining investors’ views with market equilibrium. Journal of Fixed Income 1 (2): 7–18.
Black, F. and Litterman, R. (1992) Global portfolio optimization. Financial Analysts Journal 48 (5): 28–43.
Cadenillas, A. and Pliska, S.R. (1999) Optimal trading of a security when there are taxes and transaction costs. Finance and Stochastics 3 (2): 137–165.
Cheung, W. (2010) The Black-Litterman model explained. Journal of Asset Management 11 (4): 229–243.
Chu, B., Knight, J. and Satchell, S.E. (2011) Large deviations theorems for optimal investment problems with large portfolios. European Journal of Operations Research 211 (3): 533–555.
Cvitanić, J. and Karatzas, I. (1996) Hedging and portfolio optimization under transaction costs: A martingale approach. Mathematical Finance 6 (2): 133–165.
Daniel, K. (2001) The power and size of mean reversion tests. Journal of Empirical Finance 8 (5): 493–535.
Da Silva, A.S., Lee, W. and Pornrojnangkool, B. (2009) The Black-Litterman model for active portfolio management. Journal of Portfolio Management 35 (2): 61–70.
Davis, M. and Norman, A. (1990) Portfolio selection with transaction costs. Mathematics of Operations Research 15 (4): 676–713.
Drobetz, W. (2001) How to avoid the pitfalls in portfolio optimization? Putting the Black-Litterman approach at work. Financial Markets and Portfolio Management 15 (1): 59–75.
Dumas, B. and Luciano, E. (1991) An exact solution to a dynamic portfolio choice problem under transaction costs. The Journal of Finance 46 (2): 577–595.
Fama, E.F. and French, K.R. (1993) Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33 (1): 3–56.
Fama, E.F. and MacBeth, J.D. (1973) Risk, return and equilibrium: Empirical tests. Journal of Political Economy 81 (3): 607–636.
Gatev, E., Goetzmann, W.N. and Rouwenhorst, K.G. (2006) Pairs trading: Performance of a relative-value arbitrage rule. Review of Financial Studies 19 (3): 797–827.
He, G. and Litterman, R. (1999) The Intuition Behind Black-Litterman Model Portfolio. San Francisco, CA: Goldman Sachs and Co, Investment Management Division.
Hodges, S. and Carverhill, A. (1993) Quasi mean reversion in an efficient stock market: The characterization of economic equilibria which support Black-Scholes option pricing. The Economic Journal 103 (417): 395–405.
Idzorek, T. (2007) A step-by-step guide to the Black-Litterman model. In: S. Satchell (ed.) Forecasting Expected Returns in the Financial Markets, Waltham, MA: Academic Press.
Janeček, K. and Shreve, S. (2004) Asymptotic analysis for optimal investment and consumption with transaction costs. Finance and Stochastics 8 (2): 181–206.
Jegadeesh, N. and Titman, S. (1993) Returns to buying winners and selling losers: Implications for stock market efficiency. Journal of Finance 48 (1): 65–91.
Jegadeesh, N. and Titman, S. (1995) Overreaction, delayed reaction, and contrarian profits. Review of Financial Studies 8 (4): 973–993.
Kakushadze, Z. and Liew, J. (2014) Custom v. Standardized Risk Models. SSRN Working Paper, http://ssrn.com/abstract=2493379, (8 September 2014); arXiv:1409.2575.
Knight, J. and Satchell, S.E. (2010) Exact properties of measures of optimal investment for benchmarked portfolios. Quantitative Finance 10 (5): 495–502.
Liew, J. and Roberts, R. (2013) U.S. equity mean-reversion examined. Risks 1 (3): 162–175.
Lo, A.W. (2010) Hedge Funds: An Analytic Perspective, Princeton, NJ: Princeton University Press.
Lo, W.A. and MacKinlay, A.C. (1990) When are contrarian profits due to stock market overreaction? Review of Financial Studies 3 (2): 175–205.
Magill, M. and Constantinides, G. (1976) Portfolio selection with transactions costs. Journal of Economic Theory 13 (2): 245–263.
Markowitz, H. (1952) Portfolio selection. Journal of Finance 7 (1): 77–91.
Merton, R.C. (1969) Lifetime portfolio selection under uncertainty: The continuous time case. The Review of Economics and Statistics 51 (3): 247–257.
Mitchell, J.E. and Braun, S. (2013) Rebalancing an investment portfolio in the presence of convex transaction costs, including market impact costs. Optimization Methods and Software 28 (3): 523–542.
Mokkhavesa, S. and Atkinson, C. (2002) Perturbation solution of optimal portfolio theory with transaction costs for any utility function. IMA Journal of Management Mathematics 13 (2): 131–151.
O’Tool, R. (2013) The Black-Litterman model: A risk budgeting perspective. Journal of Asset Management 14 (1): 2–13.
Perold, A.F. (1984) Large-scale portfolio optimization. Management Science 30 (10): 1143–1160.
Poterba, M.J. and Summers, L.H. (1988) Mean reversion in stock prices: Evidence and implications. Journal of financial Economics 22 (1): 27–59.
Rockafellar, R.T. and Uryasev, S. (2000) Optimization of conditional value-at-risk. Journal of Risk 2 (3): 21–41.
Satchell, S. and Scowcroft, A. (2000) A demystification of the Black-Litterman model: Managing quantitative and traditional portfolio construction. Journal of Asset Management 1 (2): 138–150.
Sharpe, W.F. (1966) Mutual fund performance. Journal of Business 39 (1): 119–138.
Shreve, S. and Soner, H.M. (1994) Optimal investment and consumption with transaction costs. Ann. Appl. Probab 4 (3): 609–692.
Author information
Authors and Affiliations
Corresponding author
Additional information
DISCLAIMER: The correspondence address is used by the corresponding author for no purpose other than to indicate his professional affiliation as is customary in publications. In particular, the contents of this article are not intended as an investment, legal, tax or any other such advice, and in no way represent views of Quantigic® Solutions LLC, the website www.quantigic.com or any of their other affiliates.
1received his PhD in Theoretical Physics from Cornell University, was a Postdoctoral Fellow at Harvard University, and an assistant professor at the C.N. Yang Institute for Theoretical Physics at Stony Brook. Dr Kakushadze received the Alfred P. Sloan Fellowship in 2001. After expanding into quantitative finance, he was a Director at RBC Capital Markets, Managing Director at WorldQuant, Executive Vice President at Revere Data, and currently is the President and co-owner of Quantigic® Solutions, an Adjunct Professor at UConn, and a Full Professor at Free University of Tbilisi. He has 90+ publications in Theoretical Physics and Quantitative Finance.
Rights and permissions
About this article
Cite this article
Kakushadze, Z. Mean-reversion and optimization. J Asset Manag 16, 14–40 (2015). https://doi.org/10.1057/jam.2014.37
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1057/jam.2014.37


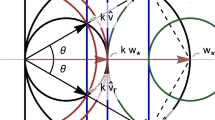

 refers to the cross-sectional mean return (not the time series mean return). Also,
refers to the cross-sectional mean return (not the time series mean return). Also,  ,
, 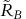 and
and  (see below) refer to the deviation from the mean return
(see below) refer to the deviation from the mean return 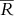 .
.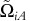 – recall that
– recall that  where
where  is the Cholesky decomposition of the factor covariance matrix Φ. However, a rotation Y→YU by an arbitrary nonsingular m × m matrix U
ab
does not change the constraints (66).
is the Cholesky decomposition of the factor covariance matrix Φ. However, a rotation Y→YU by an arbitrary nonsingular m × m matrix U
ab
does not change the constraints (66).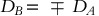 (recall that σ
A
=σ
B
). If R
A
=±R
B
, then the two instruments A and – long for plus sign and short for minus sign – B are indistinguishable for optimization purposes.
(recall that σ
A
=σ
B
). If R
A
=±R
B
, then the two instruments A and – long for plus sign and short for minus sign – B are indistinguishable for optimization purposes. can be assumed to be static.
can be assumed to be static.