A numerical and analytical study is made of the macroscopic or homogenized mechanical response of a random isotropic suspension of liquid n-spherical inclusions (n = 2, 3), each having identical initial radius A, in an elastomer subjected to small quasistatic deformations. Attention is restricted to the basic case when the elastomer is an isotropic incompressible linear elastic solid, the liquid making up the inclusions is an incompressible linear elastic fluid, and the interfaces separating the solid elastomer from the liquid inclusions feature a constant initial surface tension γ. For such a class of suspensions, it has been recently established that the homogenized mechanical response is that of a standard linear elastic solid and hence, for the specific type of isotropic incompressible suspension of interest here, one that can be characterized solely by an effective shear modulus _n in terms of the shear modulus μ of the elastomer, the initial elasto-capillary number eCa = γ/2μA, the volume fraction c of inclusions, and the space dimension n. This paper presents numerical solutions—generated by means of a recently introduced finite-element scheme—for _n over a wide range of elasto-capillary numbers eCa and volume fractions of inclusions c. Complementary to these, a formula is also introduced for _n that is in quantitative agreement with all the numerical solutions, as well as with the asymptotic results for _n in the limit of dilute volume fraction of inclusions 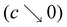and at percolation 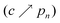. The proposed formula has the added theoretical merit of being an iterated-homogenization solution.