Introduction

Currently, graphite is the main anode materials for commercial lithium ion batteries (LIBs) due to its ability to cause reversible intercalation/deintercalation of Li+ ions in the layered structure1. However, its low Li storage capacity (372 mAhg−1) cannot satisfy the large power demanding for electric vehicles and smart grids2,3. Transition metal dichalcogenides (TMDs) with graphite-like layered structures, such as WS24, MoS25,6, MoSe27, TiS28 have received tremendous attention as alternatives to graphite for the anode materials in the rechargeable ion batteries. In the layered TMDs, anions constitute hexagonal close-packed layers, and transition metals are sandwiched between layers of anions to form two-dimensional layers with atoms covalently bonded. The two-dimensional layers are stacked together through weak van der Waals interactions between the TMD layers9, which allows the Li+ and Na+ ions to diffuse without a significant increase in volume expansion and thus prevents the pulverization problem of active materials caused by the repeated intercalation/deintercalation. The layered TMDs such as MoS2 have attractive specific capacities of Li storage, for example, MoS2/graphene nanocomposites exhibited a high specific capacity of 1225–1400 mAh/g10,11, and still had a capacity of 1351 mAh/g after 200 repeated charge-discharge cycles12.

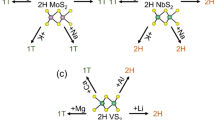
The TMDs have a variety of polytypic structures depending on the arrangement of the chalcogen atoms. The transition metal atoms have six-fold coordinates and are hexagonally packed between two trigonal atomic layers of chalcogen atoms. One polytype is based on trigonal symmetry (2H), where the chalcogen atoms are located in the lattice positions of a hexagonal close-packed structure. The metal atoms are sandwiched between two atomic layers of chalcogen in a trigonal prismatic geometry. Another polytype is based on the metal atoms octahedrically or disordered octahedrically located in the environment of the chalcogen atoms. As shown in Fig. 1, the layers are composed by prismatic D3h-, octahedral Oh-, and octahedral Oh-disordered MoS2 units, which are termed as 2H-, 1T- and 1T’-MoS2, respectively13. The electronic properties of the TMDs show a significant dependence on the polytypic structures13, for example, the 2H-MoS2 phase shows a semiconductor nature, whereas the 1T-MoS2 phases show a metallic character6,14,15. The electronic properties of the TMDs can be tuned by applying strain16 or formation of heterostructures17,18.

Figure 1: Atomistic configuration of MoS2.
figure 1

Top and side views of the (a) 2H-, (b) 1T- and (c) 1T’-MoS2. The Mo atoms have octahedral and trigonal prismatic coordination in the 1T/1T’- and 2H-MoS2, respectively.

Full size image

MoS2 and its associated composites have been investigated as anode materials for rechargeable LIBs and sodium ion batteries19,20,21,22,23 through intercalation mechanisms. As mentioned above, 2H-MoS2 has a stable crystal structure with a semiconductor character24, whereas the metastable 1T/1T’-MoS2 phase was introduced inside the 2H-MoS2 by intercalating alkali metals25. Using in-situ transmission electron microscopy (TEM) technique, a real time imaging characterization of the electrochemical process at the atomic level was performed to investigate the atomistic mechanisms of the 2H-1T/1T’ transition in the MoS2 upon lithium or sodium intercalation26,27,28. A shear mechanism of the 2H-1T/1T’ phase transition has been identified by probing the dynamic phase boundary movement27. The stability of the 2H- and 1T-LiMoS2 has also been investigated as functions of the Li content and intercalation sites29,30, and results showed that the critical content of lithium, required for the initialization of the 2H→1T phase transition, was estimated to be x ≈ 0.4 in LixMoS229.

Apart from the alkali metals, whose intercalation could induce 2H→1T/1T’ phase transition, the phase transition in the MoS2 was also reported to be caused by the substitutional doping of Mo by Re atom31, in which Re has one more valence electron than Mo. The 2H-1T’ phase transition was also reported to be induced by using a high dose electron beam irradiation during heating the MoS2 monolayer32 or by using hot electrons generated by plasmonic nanoparticles deposited onto a MoS2 monolayer33.

However, currently the mechanisms of the structural transformation from 2H→1T/1T’ induced by various methods, such as alkali metals intercalation, Re-doping, electron irradiation and hot electron doping, are not fully understood. As the metastable 1T-MoS2 shows enhanced magnetism34 and can be used as electrode materials for supercapacitors35, understanding the mechanisms of these structural transformations is crucial to improve the battery performance, material design and practical applications.

The MoS2 shows layer-dependence electronic properties36,37,38. The valence bands of the monolayer MoS2 are distinctly different from those of few-layer and bulk MoS2, and the valence band maximum of a MoS2 monolayer is located at K point of the first Brillouin zone (BZ), rather than at Г point in a bulk MoS236. Electrocatalysis of the MoS2 for hydrogen evolution also showed this layer dependent behaviour39. If the layered MoS2 is used in the anode materials for rechargeable ion batteries, the interstitial sites between the adjacent layers provide different adsorption sites compared with those of a monolayer MoS2. The MoS2 materials studied in the literature have various properties of size, morphology and number of layers19,20,21,22,23. The dependence of structural transformation on the layer number has not been investigated. Therefore, it is imperative to obtain a comprehensive understanding of the structural transformation in different layered MoS2.

In this paper, for the first time, the origin or mechanism of the structural transformation of mono-and bi-layers MoS2 was investigated using a density functional theory (DFT). Based on the results from the first principle calculation, we concluded that the electron transfer is the key reason for the structural transformation of the 2H→1T’ in the MoS2.

Results

The lattice parameters of the 2H-MoS2 mono-and bi-layers after a full structural optimization using the DFT are a = b = 3.19 Å, which are consistent with the previously calculated values of 3.18–3.19 Å40,41 and experimental value of 3.20 Å42. Those of the 1T’-MoS2 are a = b = 3.18 Å. It was reported that there are several types of stacking sequences for the bilayer MoS2 synthesized using chemical vapour deposition method43,44,45. Changing the stacking sequence can tune the electronic properties of the bilayer MoS2. The DFT simulations showed that the bilayer MoS2 with AA’ stacking sequence is energy favorable than the other types of stacking sequences46. In AA’ stacking sequence, the top layer Mo (S) atoms align vertically with the bottom layer S (Mo) atoms. In this work, we modeled the structural transformation of the bilayer MoS2 with AA’ stacking sequence.

2H→1T’ phase transition in MoS2 upon electron doping

A 2 × 2 hexagonal supercell of the MoS2 layers was used to study the stability of both the 2H- and 1T’-MoS2. The 1T-MoS2 monolayer can maintain its structure with a 1 × 1 supercell, however, it will change into the 1T’ structure when a 2 × 2 supercells was used. This phenomenon was also reported by Kan et al.47. First principles analysis shows that the instability of the 1T-MoS2 is caused by the instability of phonon dispersion at M-point48. A distorted structure of 1T-MoS2 phase, i.e. the 1T’-MoS2, can be stabilized by dimerization of Mo atoms48,49,50, as shown in Fig. 1(c). The calculated three nearest Mo-Mo distances are 2.775, 3.193, and 3.825 Å, which agree with the previous simulation values of 2.769, 3.175 and 3.808 Å51. Based on the analysis, we did not find any layer dependent dimerization of the Mo atoms. The 1T’-MoS2 is 0.26 eV per formula unit (eV/f.u.) energy lower than that of the 1T-MoS2 for both mono- and bi-layers. To investigate the stability of both the 2H- and 1T’-LiMoS2, extra numbers of electrons were injected into the MoS2 lattices instead of the traditional method of increasing the Li adsorption to characterize the modified electron density29,30. Figure 2 shows the energy difference per MoS2 molecule between the 2H- and 1T’-phases, ΔE = E1T’ − E2H, as a function of extra electron concentration. The 2H-phase is more stable than 1T’-phase at lower electron concentrations, and it is also energetically stable (with an energy difference value of 0.54 eV/f.u.) than the 1T’-phase without addition of electrons, which agrees well with the value of 0.55 eV/f.u. reported by Esfahani et al.30 and 0.51 eV/f.u. reported by Kan et al.47. The 1T’-phase becomes more stable with increasing the electron concentration, i.e. a 2H→1T’ phase transition will occur by increasing the electron concentration. The critical values of adding extra electron concentrations to trigger the 2H→1T’ phase transition were calculated to be 0.78 and 0.55 e/f.u. for the mono- and bi-layers, respectively. For the bulk LixMoS2, the critical value of x was predicted to be 0.4 for the 2H→1T structural transformation29. Therefore, our results showed that the critical electron concentration for the 2H→1T’ phase transition decreases with the increase of thickness of MoS2 layers.

Figure 2: Energy stability of 2H- and 1T’-MoS2.
figure 2

Energy difference per MoS2 molecular between the 2H- and 1T’-phase as a function of extra electron concentration. The critical extra electron concentrations for the 2H→1T’ phase transition are 0.55 and 0.78 e/f.u. in mono- and bi-layers, respectively.

Full size image

Adsorption of Li/Na on 2H-MoS2

Li/Na adsorptions on the mono- and bi-layers 2H-MoS2 were investigated using a 6 × 6 MoS2 hexagonal supercell to avoid periodical image interactions. All the previous investigations41,42 showed that both the Li and Na prefer to occupy the top of the molybdenum site (T) compared with center of the hexagon site (H) on the mono-layer of the 2H-MoS2. There are two preferred positions for the Li/Na intercalation into the interlayer spaces for MoS2 bi-layers: (1) an octahedral site enclosed by six S atoms; and (2) a tetrahedral site enclosed by four S atoms. These interstitial sites are corresponding to the T and H sites in the monolayer MoS2. Figure 3 shows the side-view and cross-section view of the adsorption sites. We calculated the adsorption energy values of Li/Na on the MoS2 using Eads = EMoS2+Li/Na − EMoS2 − ELi/Na, where EMoS2+Li/Na and EMoS2 are the total energies of MoS2 with and without Li/Na adatom adsorption, respectively. The adsorption energy can be calculated reference to adatom either in vacuum (modeled as an isolated atom in a supercell of size 30 × 30 × 30 Å3) or in bulk metal. ELi/Na is the energy of an isolated Li/Na atom or half of the energy body center cubic Li/Na bulk metal. A negative value of the adsorption energy indicates a thermodynamic favorable intercalation process.

Figure 3: Atomistic configuration of Li/Na adsorbed MoS2.
figure 3

(a) Side-view and (b) cross-section views of the possible adsorption sites for Li/Na in bi-layers 2H-MoS2.

Full size image

The calculated adsorption energies of the Li/Na in the monolayer and bilayer 2H-MoS2 are listed in Table 1. The calculated adsorption energies are −1.8 and −1.6 eV for the Li to be adsorbed at T and H sites on mono-layer 2H-MoS2, respectively, which agree well with the previous report of Li prefer to occupy the T site52,53. The adsorption energy of the Na adsorbed at the T site on the 2H-MoS2 is −1.3 eV, which is 0.1 eV energy lower than that adsorbed at the H site. It was reported that the Na cannot penetrate through the surface monolayer of MoS2, and it prefers to stay on the surface of (0001) of MoS254. whereas K can be intercalated into the interlayer spaces of MoS2 crystal55.

Table 1 Calculated adsorption energies (in eV) versus vacuum (V) and bulk metal (B) reference states for Li and Na in mono- and bi-layers MoS2.
Full size table

It was found that the adsorption energy value of the octahedral site is 0.12 eV lower than that of the tetrahedral site for Na adsorbed in the bi-layers of the 2H-MoS2. However, the Li prefers to occupy the tetrahedral site. It was also obtained that the Li and Na all prefer to occupy the interlayer position than the surface of the 2H-MoS2. Previous simulation results also showed that the Li prefers to be in the interlayer space than on the surface in bi-layers graphene56.

Charge distribution in MoS2 upon electron doping and Li/Na adsorption

The effects of extra numbers of electrons by the electron injection were studied using the equation (1) based on the differences in charge densities in the MoS2 with and without electron doping,

where and are the charge densities of the MoS2 with and without electron injection at position r , respectively. The electron injection was performed by adding electrons into the cell, and a compensating background was used to achieve the charge neutrality57. This was done by immerging the original charged system into a jellium background which fills the cell, and then neutralizing the charge to keep the net charge to be zero58. The redistribution of charge densities of Li/Na adsorbed MoS2 systems was calculated using the equation (2),

where and are the space charge densities of the MoS2 with and without Li/Na adsorption, respectively. is the electron charge density of an isolated Li/Na at the same position in the supercell as in the Li/Na- MoS2 systems.

The obtained charge distributions of monolayer 2H-MoS2 injected with 0.25, 0.75, and 1.00 e/f.u. for the mono-layer MoS2 are shown in Fig. 4(a–c). The red and green surfaces correspond to gains and loss of charges, respectively. There is no apparent redistribution of charge for the MoS2 doped with electron injection concentrations of 0.25 e/f.u. or below. With increasing the electron injection concentrations, there is an apparent loss of electronic charges from the Mo-S bonds, whereas there is a net gain of electronic charge surrounding the Mo atoms. The distribution of electronic charge on the Mo atom shows an orbital characters of dz2 59, indicating that the doped electrons and the lost electrons from the Mo-S bonds all fill the Mo dz2 orbital. The phenomenon of electron doping leading to occupation of the conduction band minimum (CBM) was also reported by Chakraborty et al.60. The transfer characteristic of the top-gated single-layer MoS2 transistor device showed an on-off ratio of ~105 and a field-effect mobility of 50 cm2/Vs with electron doping of ~2 × 1013/cm2 60. The differences of charge densities for the Li and Na adsorbed MoS2 systems are shown in Fig. 4(d,e), respectively. The electronic charge surrounding Li/Na decreases, resulting in a net loss of electronic charge of the Li/Na. There was a charge loss on the Mo-S bonds at the Li/Na adsorption site on MoS2. A net gain of electronic charge in the Li/Na-S bonds and Mo dz2 orbital can be observed. The Li/Na donate their electrons to the CBM of the 2H-MoS261, which results in an n-type doping character of Li/Na adsorbed 2H-MoS2 systems. The same phenomenon has been reported Li-doped graphene systems62,63,64,65. The bonding of Li/Na adatoms appears to be primarily ionic bonding66, which is same with that in Li intercalated graphene system67,68.

Figure 4: Charge distributions of monolayer 2H-MoS2.
figure 4

Isosurface (0.003 e/Å3) of the charge distributions of 2H-MoS2 doped with (a) 0.25, (b) 0.75, (c) 1.00 e/f.u., (d) Li and (e) Na on monolayer 2H-MoS2. The red and green surfaces correspond to charge gains and loss of charge, respectively.

Full size image

The charge distributions of the bi-layers 2H-MoS2 injected with 0.25, 0.75, and 1.00 e/f.u. electron and Li/Na adsorption are shown in Fig. 5, which shows the same characteristics as those of the mono-layer 2H-MoS2.

Figure 5: Charge distributions of bi-layer 2H-MoS2.
figure 5

Isosurface (0.003 e/Å3) of the charge distributions of 2H-MoS2 doped with (a) 0.25, (b) 0.75, (c) 1.00 e/f.u., (d) Li and (e) Na on bi-layers 2H-MoS2. The red and green surfaces correspond to charge gains and loss of charge, respectively.

Full size image

Discussion

Within the framework of crystal field theory, the energy of the 4d orbitals of Mo ions will be affected by the arrangement of surrounding negative ions. The five 4d orbitals are initially degenerate (have the same energy). Placing six negatively charged ions at the vertices of an octahedron does not change the average energy of the 4d orbitals, but will remove their degeneracy. As the Mo atom is in trigonal prism coordination sites in the 2H-MoS2, the five degenerate 4d orbitals are split into (1) one singly degenerate state dz2 (filled), (2) two doubly-degenerate states dx2 − y2, dxy (empty), and (3) two doubly-degenerate states dxz, dyz (empty), as shown in Fig. 6(d). Whereas the Mo 4d orbitals of an Oh-MoS6 unit in the 1T-MoS2 can be separated into two groups: (1) three degenerated dxz, dyz and dxy orbitals occupied by two electrons; and (2) non-occupied dz2 and dx2 − y2 as shown in Fig. 6(f). Incomplete occupation of the degenerated orbitals leads to the metallic ground state of the 1T-MoS2, and also decreases lattice stability compared with that of the 2H-MoS269. As the 1T-MoS2 is doped with electrons, the extra electrons will occupy the dxz, dyz and dxy orbitals, thus increasing the stability of the 1T-MoS2. When such kind of doping occurs in the semiconducting 2H-MoS2, the extra electrons occupy the dx2 − y2 and dxy states, thus resulting in a metallic-like character of the electronic structure and destabilization of the lattice31.

Figure 6: Orbital states.
figure 6

Partial density of states of (a) 2H- and (b) 1T’- monolayer MoS2. Isosurface (0.003 e/Å3) of the charge distributions of (c) 2H- and (e) 1T’- MoS2 doped with 1.00 e/f.u. Within crystal field theory, the Mo 4d orbitals (d) D3h- and (f) Oh-MoS6 unit will split into three and two groups, respectively.

Full size image

The partial density of states (PDOS) of 2H- and 1T’- monolayer MoS2 are shown in Fig. 6(a,b), respectively. The 2H-monolayer MoS2 shows a semiconductor character with a band gap of 1.70 eV. The electronic states near the valence band maximum (VBM) and CBM are mainly composed of Mo 4dz2, 4dx2 − y2 and 4dxy, whereas the Mo 4dxz and 4dyz orbitals do not contribute to the energy states near the VBM and CBM, which agrees with the literature17,18,70. The 1T’- monolayer MoS2 shows a metallic-like character. The extra electrons either from injection or from ion intercalation doping occupy the Mo 4dz2, and induce loss of charges from the Mo-S bonds, which will destabilize the lattice of the 2H-MoS2 as shown in Fig. 6(c). On the contrary, there is no loss of charge from the Mo-S bonds in the 1T’-MoS2.

From the charge distribution shown in Fig. 6(e), the extra electrons occupy the S 3p and Mo orbitals of dxz, dyz and dxy59. This explains the stabilization of the 1T’ structure upon Li/Na adsorption or electron doping. The electron doping destabilizes the crystal structure of the 2H-MoS2, and causes the structural transformation into the 1T’ phase through the re-distribution of the Mo 4d orbitals.

Conclusion

The stability of 2H- and 1T’-MoS2 for both the mono- and bi-layers upon electron doping was investigated using the density functional theory, and then linked with that for Li/Na intercalation process. After doping with electrons, the 2H- and 1T’-MoS2 show semiconductor and metallic characters, respectively. The extra electrons either from charge injection or from ion intercalation doping occupy the Mo 4dz2 in 2H-MoS2, and induce loss of electronic charge from the Mo-S bonds. Whereas, the extra electrons occupy the S 3p and Mo orbitals of dxz, dyz and dxy in the 1T’-MoS2 without apparent loss of electronic charge from the Mo-S bonds. Whereas electron doping destabilizes the crystal structure of the 2H-MoS2, and causes its structural transformation into the 1T’ phase through the redistribution of the Mo 4d orbitals. The critical values of electron concentrations for the 2H→1T’ phase transition decrease with increasing the layer thickness.

Simulation details

The stability of 2H- and 1T’-MoS2 and Li/Na adsorption behavior in the two polytypic structures were investigated using first principles plane-wave simulations based on DFT as implemented in the Vienna ab initio simulation package (VASP)71. Electron-ion interaction and electron exchange-correlation were described using the projector augmented wave (PAW) method72 and the generalized gradient approximation was described using the Perdew-Burke-Ernzerhof (PBE) function, respectively. An energy cutoff of 520 eV was used for the plane wave basis sets. Spin-polarization was considered applied for all the simulations.

A 2 × 2 supercell of MoS2 monolayer was used to investigate the stability of 2H- and 1T’ phases with mono- and bi-layers of MoS2. A 6 × 6 supercell of MoS2 monolayer was used to investigate the adsorption of Li/Na. A 25 Å vacuum space were constructed to avoid the periodical image interactions between two adjacent MoS2 layers. The Brillouin zone was integrated using the Monkhorst-Pack scheme73 with 5 × 5 × 1 k-grid. All the atomic positions and cell parameters were relaxed until the force on each atom is less than 0.02 eV/Å. Electron concentrations of 0.125–1.00 e/f.u., i.e. 0.14–1.13 × 1015/cm2 and 0.28–2.26 × 1015/cm2 were injected into the mono- and bi-layer MoS2, respectively, to investigate the stability of 2H- and 1T’-MoS2.

Additional Information

How to cite this article: Sun, X. et al. Origin of Structural Transformation in Mono- and Bi-Layered Molybdenum Disulfide. Sci. Rep. 6, 26666; doi: 10.1038/srep26666 (2016).