Introduction

In 2006, Pendry, Schurig and Smith1 showed that upon a transformation applied to a certain region of space, one could obtain a phenomenon of optical invisibility via highly heterogeneous and anisotropic meta-materials whose permittivity and permeability directly result from the space transformation. Leonhardt proposed a similar route to cloaking based upon a conformal map preserving right angles, which makes the required meta-materials isotropic2, but this only works for a certain frequency range. Following these works, similar techniques have been used to generalize these concepts to acoustics and mechanics. In 2012, some of us proposed to extend concepts of cloaking to diffusion processes, such as heat fluxes3, which led to first experimental demonstrations4,5,6,7 in the transient regime. Interestingly, cloaking can be also applied to mass diffusion in a very similar manner8 (this may open a new range of biomedical and chemical engineering9 applications as well as light diffusion10).

This paper is focused on the analysis of the cloaking effectiveness in the case of heat diffusion. Indeed numerous studies point out the solution of ideal cloaking but fewer evaluate in a quantitative way the resulting effectiveness after the homogenization procedure. To reach this goal the effectiveness is here characterized by a root-mean square calculated on the line fluxes, a value which would be zero in the case of a homogeneous medium. Such characteristics allow us to compare different homogenized cloaks and emphasize their advantages and weaknesses. Moreover, rather than analyzing the effectiveness at each time step, we prefer to perform a spectral analysis, on the basis of the classical time-frequency analogy. Hence we work in the frequency or time harmonic regime and investigate the spectral effectiveness of various homogenized cloaks. Such harmonic study can be implemented if one consider a heat source generated by a modulated laser beam for instance. We first investigate both ideal (singular and non singular) cloaks and approximate cloaks. Then, we improve earlier attempts to design multi-layered thermal cloaks3,11 using the two-scale convergence method introduced in ref. 12 and further developed by ref. 13. We show that our improved design reduces by at least one order of magnitude the standard deviation of thermal isovalues compared to earlier designs. Potential applications are in thermal metamaterials and the management of heat flux.

Results

Quantitative analysis of different ideal heat cloak effectiveness Space transformation and singularities

Changes from polar coordinates (r, θ) to radially stretched polar coordinates (r′, θ′) = (f(r), θ) applied to the heat equation (19) gives us the transformed conductivity and transformed product of heat capacity and density3

where we have

and g is the reciprocal function of the monotonic function f, is the derivative function of g, R is the rotation matrix through an angle θ and RT its transpose. Note that these parameters hold for the transformed heat equation written in time or frequency domains (see Sec. Methods). Also, in the static limit, the product ρ′c′ does not appear in (1) and one need only consider the anisotropic heterogeneous conductivity in (1) to obtain the desired management of heat flux. Notice that a particularly appealing application of the transformed heat equation is thermal cloaking14. It can be more convenient to write relations (1–2) versus the variable r = g(r′), with . The result is:

These last equations directly recall that singularities occur at r′ = f(r)|r = 0, a radius where is zero and infinite, while ρ′c′ depends on the behaviour of f around the origin. This is true whatever the transformation f though r = 0 does not necessarily concern the transformed region. Note in passing that a spherical (3D) diffusion cloak would have a different kind of singularity, with the radial component of the conductivity vanishing at the inner boundary of the cloak, while the other two are constant8.

Specific transformations

Now different f functions can be used to obtain a simple design of ideal cloak by mapping a ring εR1 ≤ r ≤ R2 (with ) into another ring R1 ≤ r′ ≤ R2. The following conditions must be fulfilled

Depending on whether ε < 1 or ε > 1, the f transformation characterizes a contraction or dilatation, respectively. A basic transformation may consist in a polynomial function .

Pendry's and Milton's cloaks1,15 were based on linear (N = 1) and quadratic (N = 2) maps, respectively. Both also used ε = 0, which means that the whole disk 0 ≤ r ≤ R2 is transformed into the ring R1 ≤ r′ ≤ R2. With N = 1 (Pendry), we obtain

which leads to

with varying in the range , in the range and ρ′c′ in the range when r′ ∈ [R1, R2]. We note the discontinuity of , and ρ′c′ with the parameters of the surrounding medium at the interface r′ = R2.

With N = 2, one of the an coefficients (namely a1 or a2) can be arbitrarily chosen. To remove such an indetermination Milton proposed to ensure the continuity of the transformed conductivity and ρ′c′ product at r′ = R2. We can see from (3) that this continuity at r′ = R2 amounts to ensure that giving the following expressions on the an coefficients

This gives us

and . and both vary in the range [0, 1] and we have ρ′c′ ∈ [0, ρc] when r′ ∈ [R1, R2]. Then, we clearly see that the continuity of , and ρ′c′ is ensured at the interface r′ = R2 with the surrounding media.

The case ε ≠ 0 avoids the singularity at r′ = R1. With N = 1, Kohn16 obtained and leading to

with varying in the range , in and ρ′c′ in when r′ ∈ [R1, R2]. If ε → 0, we retrieve the expressions from (6).

A summary of the thermal parameters' behaviour is given on Fig. 1 for different cloaks. Notice that with a general polynomial transformation the coefficients would be written as an = an(ε, N). Other transformations could be used. With an exponential function we obtain .

Figure 1
figure 1

Normalized conductivity and product ρc parameters used for Pendry (green), Kohn (black) and Milton (magenta) cloaks as a function of r′ inside the cloak.

The inner boundary of the cloak is R1 = 0.15 mm and the outer boundary is R2 = 2R1 = 0.3 mm. We used here ε = 0.1 for Kohn's cloaks.

Full size image

Implementation and effectiveness of ideal cloaks

We study the three cloaks introduced above using the commercial finite element package COMSOL Multiphysics ®. Our two-dimensional simulation consists of the resolution of the time-harmonic heat equation (see Sec. Methods) in a 5 mm by 0.8 mm computational domain containing the studied cloak. The medium surrounding the cloak corresponding to the region r′ ≥ R2 is made of Titanium of thermal conductivity κTi = 22 W.m−1.K−1 and product of density by heat capacity ρcTi = 2.35 × 106 J.kg−1.K−1 giving a thermal diffusivity aTi ≈ 1.10−5 m2.s−1. Then, the initial ring of thickness R2 − εR1 is mapped onto the ring of thickness R2 − R1. This latter ring corresponds to the invisibility cloak whose parameters are shown on Fig. 1 depending on which transformation we choose (Pendry, Milton or Kohn). The effect of the cloak within [R1, R2] is to straighten the isotherms for for r′ > R2 as if we were in an homogeneous medium. The inner and outer radii of the cloak are chosen to be respectively R1 = 0.15 mm and R2 = 0.3 mm. Finally, the region 0 ≤ r′ ≤ R1 (mapped from the initial region 0 ≤ r ≤ εR1) contains the cloaked object. It is made of polyvinyl chloride (PVC) of thermal conductivity κPVC = 0.15 W.m−1.K−1 and product of density by heat capacity ρcPVC = 1.33 × 106 J.kg−1.K−1 of thermal diffusivity aPVC ≈ 1.10−7 m2.s−1.

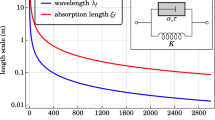
Notice that the 5 mm length of our computational domain has been chosen in such a way that it is in accordance with the thermal diffusion length D in Titanium at angular frequency ω = 1 rad.s−1, . Regarding the boundary conditions, we chose to set the temperature to T0 = 1 K on the left boundary of the computational domain and Tf = 0 K on the right boundary of the computational domain so that heat diffuses from left to right (namely from x = −2.5 mm to x = 2.5 mm). As for the upper and lower boundaries of the computational domain, we chose Neumann (perfect insulating) conditions .

Now the main idea to determine quantitatively the effectiveness of a cloak is to evaluate the standard deviation of the isotherms in the vicinity of the cloak. A theoretical perfect cloak would give a zero standard deviation for all the isotherms outside the cloak as if the medium was completely homogeneous, which is clearly not the case in Fig. 2.

Figure 2
figure 2

Map of a thermal cloak in the static limit (left) with a close-up on the isotherms in its vicinity (right).

The cloak's inner boundary is R1 = 0.15 mm and its outer boundary is R2 = 0.3 mm and it consists of 10 layers of identical thickness with thermal parameters given in Table 1.

Full size image

Thus, by evaluating the standard deviation of the isotherms (see Sec. Methods) for different cloaks, we can quantitatively determine the effectiveness of a cloak. All isotherms are calculated before and after the outer radius of the cloak in the incident diffusion direction and we define the standard deviation ratio

where std(bare object) denotes the standard deviation of the isotherms when heat diffuses through the bare object to be cloaked and std(studied cloak) is the standard deviation of the isotherms when the ideal cloak under study is around the object. An efficient cloak means that std(studied cloak) is close to 0. Therefore the standard deviation ratio increases with increasing effectiveness.

In Fig. 3, we compare the standard deviation ratio of the isotherms resulting from a single insulating homogeneous layer made of clay of thermal conductivity κclay = 1.28 W.m−1.K−1, product of density by heat capacity ρcclay = 1.28 × 106 J.kg−1.K−1 (thermal diffusivity aclay ≈ 1.10−6 m2.s−1) in red, a perfect cloak (Pendry) calculated with ε = 0 and N = 1 (green), a perfect cloak (Kohn) calculated with ε ≠ 0 and N = 1 (black) and a perfect cloak based on the Milton transformation (magenta) calculated with ε = 0 and N = 2. Moreover calculation is performed at different frequencies, in a range appropriate with the thermal diffusion length and the deviation is plotted versus the average diffusion direction.

Figure 3
figure 3

Standard deviation ratio of a clay homogeneous monolayer cloak (red), Pendry's cloak (green), Kohn's cloak (black) and Milton's cloak (magenta) at angular frequencies ω = 0, 0.1, 1 and 3 rad.s−1.

The source is on the left so that heat diffuses from left to right. The vertical lines are related to the position of the insulating layer and cloaks. The (z) vertical axis gives the ratio of the deviation on a logarithmic scale, while the (x) horizontal axis is for the temperature of the isotherms. Note that this temperature scale is directly connected to the x length coordinate. For the static regime for instance the temperature is at half of the total x length. This is no longer the case at increasing frequencies, which explains the shift of the curves with frequency ω. The horizontal dashed blue line indicates the height of minimum of the standard deviation ratio among all the studied cloaks at frequency ω.

Full size image

In Fig. 3, the horizontal blue line at altitude 1 is for the bare object, which is a hallmark of neutral effectiveness. We first notice that the clay monolayer cloak is below this curve, which means that the deviation has been increased. On the other hand, as expected we observe in the vicinity of the cloak that the ideal Pendry and Kohn cloaks reduce the deviation by a factor of nearly 105 for ω = 0; rad.s−1, which emphasizes a great effectiveness. The Milton cloak appears to be less efficient, but this is due to the fact that Milton's transformation is defined for a whole range of radii R2 ≥ 2R1 while we considered R2 = 2R1 in our case. The Milton cloak is therefore used in a critical regime explaining its lower performances at this given mesh. A design of Milton's cloak with R2 > 2R1 reaches identical effectiveness to that of Pendry's and Kohn's cloaks as we can see in Fig. 4.

Figure 4
figure 4

Standard deviation ratio of Milton's cloaks at angular frequencies ω = 0 rad.s−1 with R2 = 2R1 (red), R2 = 2.5R1 (green) and R2 = 3R1 (black).

Note that the black curve is similar to green (Pendry's cloak) and black (Kohn's cloak) curves in the upper left panel of Fig. 3. The horizontal dashed blue line indicates the height of minimum of the standard deviation ratio among the studied Milton's cloaks.

Full size image

For non-zero angular frequency, the curves of effectiveness are shifted towards the zero temperature as increasing frequencies corresponds to earlier time-step in the transient regime. Thus, at greater frequencies, the temperature did not diffuse all along the computing domain and the isotherms around the cloak are close to zero. We observe a decrease of the effectiveness for all cloaks for ω = 0.1, 1 and 3 rad.s−1 going down from 105 to 103 for the Pendry cloak for instance. This is expected as the mesh used for for the simulations were not optimized for every angular frequency, only for the static regime. Notice that optimal mesh for every angular frequency would give infinite effectiveness for all isotherms in the whole spectral range. Hence the finite effectiveness value is the result of the reference mesh we used to ensure proper finite elements calculation and its effectiveness variation (from 105 to 103) is due to the fact that the mesh is only optimized for the static regime. Notice however that such constant mesh still allows the comparison of the different cloaks at a given mesh.

Towards homogenized multi-layered heat cloaks

We now want to build thermal cloaks that have similar properties and effectiveness as those of perfect cloaks. Thus we need a tool to design thermal meta-materials that will give the desired properties. For this purpose, we make use of the homogenization process (see Sec. Methods). We start from an alternation of concentric homogeneous thin layers with respective conductivities and product of density by heat capacity (κ1, ρ1c1) and (κ2, ρ2c2) which might depend on r′. If the number of concentric layers gets large enough (and their thicknesses vanish), this alternation will behave as the required anisotropic inhomogeneous conductivity κ′ and inhomogeneous product ρ′c′ under certain conditions on κ1(r′), κ2(r′), ρ1c1(r′) and ρ2c2(r′):

We now consider the linear transformation r′ = a1r + a0 with ε = 0. Therefore, we want our homogenized cloak to behave like Pendry's cloak. Solving for κ1 and κ2 provides us with the parameters to use in the concentric multi-layered cloak:

Then, we approximate κ1(r′) and κ2(r′) by dividing radially the cloak into N elements and by taking the mean of κ1(r′) and κ2(r′) on each element. Also, we will assume ρ1c1(r′) = ρ2c2(r′) = ρ′c′. The Figure 5 shows the evolution of the conductivity and product ρc parameters as one goes from the inner boundary of the cloak (R1 = 1.5 mm) to the outer boundary of the cloak (R2 = 3 mm) for Pendry's 10-layer, 20-layer and 50-layer homogenized cloaks.

Figure 5
figure 5

Normalized conductivity and product parameters used for the Pendry's 10-layer (green), 20-layer (black) and 50-layer (magenta) homogenized cloaks as a function of r′ inside the cloak (see Table 1 for explicit values used for the 10-layer homogenized cloak).

κhom denotes either the radial average < κ1 > or < κ2 > depending on the considered radial element. ρchom denotes the radial average < ρ′c′ > on the considered radial element.

Full size image

In Fig. 6 we compare the standard deviation ratio of Pendry's cloak (red), the 10-layer homogenized cloak (green), the 20-layer homogenized cloak (black) and the 50-layer homogenized cloak (magenta) introduced above. We can see that the homogenization process gives good results as the standard deviation ratio of the homogenized cloaks increases with the number of layers used, rising from 101 for the 10-layer cloak in the vicinity of the cloak to 102 for the 50-layer cloak. As seen previously, we observe for non-zero angular frequency a decrease in the effectiveness which mainly comes from the reference mesh we used. We still see increasing effectiveness for multilayered cloak as the number of layers goes up.

Figure 6
figure 6

Standard deviation ratio of Pendry's perfect cloak (red), a 10-layer homogenized cloak (green), a 20-layer homogenized cloak (black) and a 50-layer homogenized cloak (magenta) at angular frequencies ω = 0, 0.1, 1 and 3 rad.s−1.

The source is on the left so that heat diffuses from left to right. The vertical lines indicate the position of the cloaks. The (z) vertical axis gives the ratio of the deviation on a logarithmic scale, while the (x) horizontal axis is for the temperature of the isotherms. The horizontal dashed blue line indicates the height of minimum of the standard deviation ratio among all the studied cloaks at angular frequency ω.

Full size image

However, the goal is still far off since we would like to reach a standard deviation ratio of 104 to ascertain our homogenized cloaks mimic Pendry's cloak. But we expect this gap between perfect and homogenized cloaks to depend merely on the number of layers used and the asymptotic behaviour of κ1 around r′ = R1. This point is discussed in the next section.

Discussion

To emphasize the effectiveness of the homogenized cloak, we studied a discretized version of the perfect anisotropic Pendry's cloak in (5) with ε = 0. We divide the cloak into N × M elements (N elements in the radial direction and M elements in the azimuthal directions). In each element, we take the average of the conductivity so that the resulting conductivity in this element can be written

where ri and ri+1 are the radial boundaries of the element and θi and θi+1 are the azimuthal boundaries of the element. Thus, we obtain a piecewise homogeneous anisotropic cloak. If N and M go to infinity we expect to retrieve the original anisotropic heterogeneous cloak. In Fig. 7, we compare the standard deviation ratio of a 50-layer homogenized isotropic cloak and the standard deviation ratio of a 50×5 discretized anisotropic cloak (50 layers in the radial direction and 5 layers in the azimuthal direction), a 50×10 discretized anisotropic cloak and a 50×20 discretized anisotropic cloak. As we can see, we achieve a better effectiveness with the homogenized isotropic cloak than with the discretized anisotropic cloaks, which results from the asymptotic behaviour of . Thus even compared to the effectiveness of the continuous Pendry's cloak in Fig. 6 (red), it seems that the homogenization process has fairly optimal performances as the discretized anisotropic Pendry's cloak has a much lower effectiveness for the same number of layers. We conclude that achieving effectiveness comparable to that of Pendry's perfect cloak appears to depend merely on the number N of layers used in the homogenized cloak. A finer mesh in the neighbourhood of the cloaks' inner boundary should also improve their effectiveness since this would better fit the rapid change of material parameters.

Figure 7
figure 7

Standard deviation ratio of a 50-layer homogenized isotropic cloak (red), a 50×5 discretized anisotropic cloak (green), 50×10 discretized anisotropic cloak (black) and a 50×20 discretized anisotropic cloak (magenta) at angular frequencies ω = 0, 0.1, 1 and 3 rad.s−1.

The source is on the left so that heat diffuses from left to right. The vertical lines indicate the position of the cloaks. The (z) vertical axis gives the ratio of the deviation on a logarithmic scale, while the (x) horizontal axis is for the temperature of the isotherms. The horizontal dashed blue line indicates the height of minimum of the standard deviation ratio among all the studied cloaks at frequency ω.

Full size image

Finally, we performed numerical simulations to verify the homogenization convergence behaviour as the number of layers N increases. We have the result17

where uε denotes the temperature in the computing domain Ω for a N-layer cloak and u is the limit of uε when ε → 0 (see Sec. Methods). We can also write ε as . Plotting as a function of log(N) should let us verify accordance with equation 14. Also plotting log (std(N − layer cloak)) for a given isotherm (the one tangential to the cloak for instance) as a function of log(N) would give the behaviour of the standard deviation for a given isotherm. The results are plotted on Fig. 8 and are as follows:

Figure 8
figure 8

Logarithm of the L2-norm (blue) and logarithm of the standard deviation (red), for the isotherm stated before, as a function of log(N) (the values of log(N) have been replaced by the N values for visibility).

Simulations are performed at ω = 0 rad.s−1. Linear fit and equations have been added for each curve.

Full size image

Through linear fitting, we find the linear equations

where C and C′ are constants. Thus, we can calculate the number of layers N that would be required to achieve the standard deviation of Pendry'cloak for the same isotherm. Notice that the calculated number of layers N would depend on the mesh that is used (optimized mesh will give an infinite number of layers). We choose the isotherms that are directly tangential to the cloak in the diffusion direction because they are the most difficult to straighten. Direct calculation gives the number of layers required:

We understand with this high number that building a nearly perfect cloak can be rather difficult as you will need to divide the region R2 − R1 about ten thousand times. However this study is the first one to shed light on the number of layers in thermal invisibility cloaks and enlightens us on the number of layers that should be used for a certain mesh i.e. for a certain effectiveness tolerance.

We stress that a similar analysis of the effectiveness of electromagnetic invisibility cloaks has not been performed thus far. Hence, we hope that our study will foster theoretical and numerical efforts towards a better understanding of cloak's effectiveness not only in diffusion, but also in wave phenomena.

Methods

Time-harmonic heat equation

We are here interested in a heat source resulting from the absorption of a modulated laser beam, so that the Fourier transform of temperature is introduced as:

where T is the temperature defined in our computational domain, t the time variable, ω the angular frequency and x the space variable. We then take the Fourier transform of the heat equation

leading to the time-harmonic heat equation

where u is the Fourier transform of the temperature, κ is the conductivity, ρ the density, c the heat capacity and ω the angular frequency of a periodic heat source. Note here that this equation is valid in two and three dimensions.1

Table 1 Conductivity and product ρc parameters used for the 10-layer homogenized cloak after averaging on each radial element
Full size table

Standard deviation of isotherms

The Fourier transform of the temperature u can be written like the following

with Φ depending on the position and the angular frequency ω. Thus, we retrieve the (x, y)-coordinate of the |u| curves using COMSOL Multiphysics® and perform the standard deviation of |u| for every isotherms.

Homogenization process

Following the proposal of Greenleaf and coworkers18 to apply the two-scale convergence method of G. Allaire13 and G. Nguetseng12 in the design of approximate multi-layered cloaks, we derive a set of new effective parameters for a multi-layered heat cloak. We consider an alternation of concentric layers of respective conductivities κ1 and κ2 and of respective heat capacities ρ1c1 and ρ2c2 so that the overall conductivity and heat capacities can be written

where x is the position vector, r = ||x|| is the Euclidean norm of x and is the indicator function of the set I. The function κε is periodic on the set Y = [0, 1] and ε represents its periodicity (clearly, the thinner the layers in the cloak, the smaller the positive parameter ε). In this set of concentric layers, the time-harmonic heat equation is written

where uε is the Fourier transform of the temperature and ω is the angular frequency of a periodic heat source. It is possible to show that when ε → 0, this alternation of materials behaves like an anisotropic inhomogeneous medium of conductivity

and heat capacity

where κ0 and ρ0c0 are the respective two-scale limits of κε and ρεcε when ε → 0 and are written

The homogenized time-harmonic heat equation is then written

where u is the limit of uε when ε → 0. Then, we need to solve the system

for our set of materials to work as our cloak.