Introduction

Consensus is ubiquitous in both animal and human societies1,2. For example, flocks of birds move collectively towards the same direction3,4, individuals vote to achieve an agreement whenever different opinions emerge in democratic societies5,6. Furthermore, advancements in understanding consensus have been seen in many fields, such as computer science, automatic control and distributed computing7,8,9,10,11,12. All such underlying systems that are able to reach consensus share some similarities: interactions between evolutionary individuals in structured populations. For instance, each fish only has the ability to access the local information though they move collectively as a whole. In this case, taking a fish as a node and connecting those nodes where information exchange occurs, a network is thus formed.

So far, the main attention on consensus has remained in isolated and single structures13,14,15,16, although real-world networks are composed of many interactive structures17,18,19,20,21,22,23,24,25,26,27, such as networks of networks, or interdependent populations. A key property of interdependent populations is the interaction dynamics between populations which cannot be described in the single structure framework. In particular, it is unclear how such dynamics between interdependent populations affect the consensus28,29,30,31. Here, we are interested in the consensus at the population level, where the fraction of population adopting a specified strategy (such as an opinion, a behavior, etc.) is the same across different interactive groups32,33. One example for such population-level consensus is the 2012 US presidential election in Nevada, New Hampshire and Pennsylvania: the supporters of Barack Obama are all of 52% in each state. In addition to the population structure, evolution is the driving force of the system where consensus is observed, such as the voting in human societies is evolutionary in the sense that successful opinions are likely to be adopted34,35,36,37,38,39. Evolution is so important in such systems that it is even believed that nothing makes sense except in the light of the evolution40, which inspires us to ask how selection, one of the main forces of evolution, affects the consensus?

To address this issue, we make use of a 2 × 2 game to depict the interaction of individuals between two interactive groups and investigate under what condition the asymptotically stable consensus can be reached, where the original consensus cannot be deviated given small population perturbations. Based on a fast partnership rewiring process, we arrive at a differential equation governing the frequency of the strategy in each group. Besides, we analytically show that for such 2 × 2 games (including the dominant/coexisting/bistable-type games), selection paves the avenue for the population evolving to an asymptotic stable consensus, whereas it is impossible without selection. In particular, for the coexisting type game where it is best to play the strategy opposite to one's opponent, not only the formation of an asymptotic consensus but also the speed to reach consensus is promoted by selection. These findings are in good agreement with the numerical simulations.

Model

Micro-update rules in interdependent populations

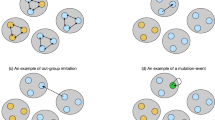
Individuals are located at nodes in interdependent populations, consisting of two interactive groups referred as Group-1 and Group-2 (See Figure 1). Note that this set-up is akin to the structure of interdependent networks, in the sense that the success of one node in a given group not only depends on the nodes in the same group, but also replies on the state of other nodes in other groups. Group-i is of size Ni (i = 1, 2), leading to the size of entire population N = N1 + N2. Initially, the average degree of Group-i is denoted as Li = 2Hi/Ni, where Hi is the total number of links in Group-i. Denote the number of links connecting two nodes in Group-i as Hii(i = 1, 2), while the number of links connecting two nodes between two groups as H12 (or H21). Then, the total number of links is H = H12 + H11 + H22.

Figure 1
figure 1

The co-evolution of strategy updating and structure switching.

Each node denotes one of two types of players, A and B, arranged in two interactive groups referred as Group-1 and Group-2, respectively. At each time step, the strategy updating happens with probability ω; the evolution of structures happens with probability 1 − ω. For rewiring partnerships during the structure evolution process, we choose neighbours in its own group with probability α and choose neighbours in the other group with probability 1 − α.

Full size image

Each player is either of strategy A or B, denoted by (1, 0)T and (0, 1)T, respectively. Here, a strategy represents an opinion/a behavior adopted by players. When two A (player with strategy A) meet, each player gets payoff a; when two B (player with strategy B) meet, each player gets payoff d. When A meets B, A gets payoff b while B gets payoff c, which leads to a payoff matrix M describing the local pairwise interaction as follows:

Without loss of generality, we assume that all payoff entries are positive. The payoff of each player is obtained by playing with all its immediate neighbors.

We consider the co-evolution of strategy and interdependent populations41,42,43,44,45. In fact, not only strategy but also social interactions between individuals are under the pressure of evolution, which leads to the entangled dynamics of strategy and structures and such co-evolution is an important source of dynamical complexity46.

At each time step, with certain probability ω, strategy evolution happens; otherwise, the evolution of structures occurs. Here, probability ω governs the dynamical time-scale of these two updating rules. When ω = 1, the strategy evolves while population structure never changes, which has been extensively addressed20,21,22,23,24. When ω = 0, no strategy evolution occurs while the topology evolves all the time. In this case, the frequency of a specified strategy in any group will never change, thus the population-level consensus in two interactive-groups cannot takes place, unless it is in the consensus state initially. The rules of strategy updating and structure switching are listed as follows:

Strategy evolution

We adopt the Fermi update dynamics47,48 to describe the strategy evolution, where individuals update their strategies by imitating the strategy of more successful individuals. At each time step (during the strategy evolution), a player is selected randomly from the whole population, namely h with payoff Ph, then a neighbor of h is selected randomly, namely g with payoff Pg. Here, is the payoff of player h (Pi,h is the payoff of player h obtained from Group-i). Then, the strategy of player h replaces that of player g with probability , where β ≥ 0 is the intensity of imitation, measuring how strong the payoff difference influences individuals' decision making.

Structure evolution

Each link is assigned a number, , as its name. To characterize the dynamics of population structure with various kinds of relationships, where players leave or break interactions when they dissatisfy with the current situation, we introduce kXY as the probability with which a XY-type link breaks. We describe the structure evolution in detail as below:

Step 1

At each time t (during the structure evolution), a link lt of type XiYj is selected from the interdependent populations at random (X, Y ∈ {A, B}, i, j ∈ {1, 2}).

Step 2

With probability 1 − kXY, the selected link lt remains unchanged, denoted as lt+ 1 = lt. With probability kXY, the selected link breaks.

Step 3

If the link is broken, one node is selected randomly from the two ends, then the selected player tries to find another player to newly connect with. With probability α, the neighbor is only selected within the same group as its friend-making candidate; otherwise, the potential neighbor is chosen from the other group. Denote this new link as lt+ 1.

Here, α is the intra-group attaching bias between two interactive groups, reflecting the propensity to rewire neighbors within the same group; and kXY is time-invariant, reflecting the structure effect of linking dynamics. Note that the inverse of kXY can be regarded as the average duration time between strategies X and Y, namely kXY is a measurement of the duration of XY link. Furthermore, the total number of links H is fixed in the co-evolution process41,43,49,50, which implies a limited resource environment. The implementation of the co-evolution of strategy and structure scheme is depicted as shown in Figure 1.

Macro-dynamics in interdependent populations

Consider the fast partnership rewiring process, i.e., , which corresponds to the case that players are much more reluctant to change strategies than to adjust their interactions49,50,51,52. In this case, the structure evolution of the interdependent populations obeys a stationary distribution when the strategy evolution occurs (See Section 2 in SI). Moreover, the average fitness of players is determined by the stationary distribution of the structure evolution. Therefore, the average fitness of strategies A and B in Group-i are

where , e1 = (1, 0), e2 = (0, 1), xi = (xi,A, xi,B)T (xi,A represents the fraction of strategy A in Group-i) and

It is worth noting that matrix M′ is a time-scaling modification of Eq. (1): every payoff entry is rescaled by the corresponding interaction time, i.e., the inverse of the breaking probability, based on what strategies the focal two players possess50. This transformation shows the complex dynamics incorporating both strategy and independent populations can be treated as a new game in a well-mixed population53. Besides, the first term in the bracket of Eq. (2) represents the payoff obtained via intra-group interactions, while the second term represents the payoff obtained via inter-group interactions. They are balanced by propensity α. This simple equation analytically captures the basic idea of the model: each player's payoff is determined on not only the structure configuration it belongs to but also that of the other group.

For large populations, the stochastic process can be well depicted by a set of stochastic differential equations referred as Langevin dynamics54. According to Eq. (2), we obtain a differential equation governing the frequency of strategy A in each group (See Section 3 in SI):

Here i, j ∈ {1, 2} and i ≠ j.

Results

Selection plays an important role in evolutionary process, which determines the direction of evolution. The absence of selective difference is called neutral selection (β = 0). When selection acts, the transition probability becomes payoff dependent, which can be further classified into constant and frequency dependent selections. Generally, the probability of one strategy replaces another is fairly complicated under frequency dependent selection55. Fortunately, many results have been obtained with the assumption of weak selection, where perturbation analysis analytically facilitates the derivation56,57. For non-weak selection, the approach of perturbation analysis does not work and the result under weak selection can be violated58.

Neutral selection: β = 0

When β = 0, the selection dynamics are neutral, in which the evolutionary direction is random and independent of the players' payoffs. In this case, Eq. (4) is simplified as

Note that the points in line x2,A = x1,A are the equilibria of Eq. (5). The corresponding eigenvalues of the Jacobian matrix at x2,A = x1,A are λ1 = 0 and λ2 = −2. Thus, the line x2,A = x1,A is always a stable manifold and system (5) always reaches consensus. Furthermore, all the consensus states are stable, but none are evolutionarily stable, i.e., final consensus can go back and forth from one state to another (See Fig. 2).

Figure 2
figure 2

System (5) reaches consensus under neutral selection (β = 0), with N1 = 150, N2 = 100, L1 = 6, L2 = 9.

(a) Phase portrait of Eq. (5) where the direction of the velocity field is indicated by the arrows. The ultimate values of the frequency of strategy A in Group-1 and Group-2 converge to the line x2,A = x1,A. (b) Simultaneous time-evolution of frequency of strategy A in Group-1 and Group-2. One of the consensus states is shown, where the initial frequency of strategy A in Group-1 and Group-2 is selected randomly.

Full size image

Weak selection: β ≪ 1

When β ≪ 1, the effects of payoff differences are small, such that the evolutionary dynamics mainly results from random fluctuations. This case of weak selection means one phenotype is slightly advantageous over another59. In evolutionary biology and population genetics, it is widely accepted that most mutations confer small selective difference60,61.

For simplicity, we assume N1 = N2. We verify the general case of N1 ≠ N2 in numerical simulations (See Figs. 3,4,5,6,7). When N1 = N2, Eq. (4) becomes

where is constant, , , , and . Note that κ only influences the time-scale with none effect on the long run evolutionary outcome.

Figure 3
figure 3

Phase portrait of Eq. (6) under weak selection (β = 0.01).

The direction of the velocity field is indicated by arrows. We set N1 = 150, N2 = 100, L1 = 6, L2 = 9, ω = 0.01. (a) When and (a = 2, b = 1, c = 1.5, d = 0, kAA = 0.4, kAB = 0.6 and kBB = 0.8), system (6) reaches an asymptotically stable consensus state of all-A. (b) When and (a = 1.5, b = 0, c = 2, d = 1, kAA = 0.6, kAB = 0.4 and kBB = 0.8), system (6) reaches an asymptotically stable consensus state of all-B.

Full size image
Figure 4
figure 4

Phase portraits of Eq. (6) under weak selection (β = 0.01).

The direction of the velocity field is indicated by arrows. We set N1 = 150, N2 = 100, L1 = 6, L2 = 9, ω = 0.01. When and (a = 1.5, b = 1, c = 3, d = 0, kAA = 0.6, kAB = 0.4 and kBB = 0.8), we show two cases of phase portraits when the intra-group bias α changes. (a) For α < α* = 0.65 (α = 0.3), the velocity field diverges to the corners near (0,1) and (1,0), which indicates that system (6) cannot reach an asymptotically stable consensus state. (b) For α > α* = 0.65 (α = 0.7), the velocity field converges to the interior equilibrium, which means that system (6) reaches an asymptotically stable consensus at the interior equilibrium.

Full size image
Figure 5
figure 5

Simultaneous time-evolution of the frequency of strategy A in Group-1 and Group-2 under weak selection (β = 0.01).

Initially, strategy A is randomly distributed in Group-1 and Group-2. We set N1 = 150, N2 = 100, L1 = 6, L2 = 9, ω = 0.01, a = 1.5, b = 1, c = 3, d = 0, kAA = 0.6, kAB = 0.4 and kBB = 0.8.

Full size image
Figure 6
figure 6

Phase portrait of Eq. (6) under weak selection (β = 0.01).

The direction of the velocity field is indicated by arrows. We set N1 = 150, N2 = 100, L1 = 6, L2 = 9, ω = 0.01. When , and α > α* = 0.65 (a = 2, b = 0, c = 1.5, d = 1, kAA = 0.4, kAB = 0.6, kBB = 0.8 and α = 0.7), the velocity field converges to the corner equilibrium E1 or E2, which means system (6) reaches an asymptotically stable consensus relying on the initialization.

Full size image
Figure 7
figure 7

Simultaneous time-evolution of the frequency of strategy A in Group-1 and Group-2 under weak selection (β = 0.01).

We set N1 = 150, N2 = 100, L1 = 6, L2 = 9, ω = 0.01, a = 2, b = 0, c = 1.5, d = 1, kAA = 0.4, kAB = 0.6, kBB = 0.8. (a) When and , system (6) reaches an asymptotically stable consensus state of all-A. (b) When but , system (6) reaches an asymptotically stable consensus state of all-B.

Full size image

From Eq. (6), we get three possible equilibria, i.e., E1 = (0, 0), E2 = (1, 1), . E1 and E2 are at the corners, which denote that system (6) is composed of all-B and all-A, respectively. E3 is an interior equilibrium, which means that system (6) consists of A and B players (See Section 4 in SI for details about the stability of each equilibrium). With different parameters ci (1 ≤ i ≤ 5), we further discuss the consensus for system (6) under weak selection.

Case 1: Consensus of the dominant-type game.

When and , strategy A dominates strategy B in the interdependent populations, if kAA < kAB < kBB. This result indicates that all players are more likely to interact with strategy A. In this case, E1 is an unstable equilibrium and E2 is a stable equilibrium, which implies that the set of all-A (E2) is the unique evolutionary stable state of this game. Let us take the prisoner's dilemma (PD) game as an example, in which strategies A and B denote defection and cooperation, respectively. The frequency of strategy A in each group converges to the state of all-A and system (6) reaches an asymptotically stable consensus state (See Fig. 3(a)).

When and , strategy B dominates strategy A in the interdependent populations, if kAA > kAB > kBB. Therefore, all players are more likely to interact with strategy B. In this case, E1 is a stable equilibrium and E2 is an unstable equilibrium. This situation is similar to that of the above discussion, which leads to the dynamics ending in the state of all-B (E1) and system (6) reaches an asymptotically stable consensus state, as shown in Fig. 3(b).

Therefore, when the interactions between players under the payoff matrix M′ are of the dominant-type game, two interactive groups reach a homogeneous consensus, i.e., the stable consensus state consists of all-A, or all-B.

Case 2: Consensus of the coexisting-type game.

When , and , both E1 and E2 are unstable and E3 is a saddle point, if kAA > kAB and kBB > kAB. This implies that all players are inclined to interact with the opponents of opposed strategies as themselves'. In this case, the velocity field is out of order and system (6) cannot reach a consensus state (See Fig. 4(a)). However, when the intra-group attaching bias α exceeds the critical value α*, E3 becomes stable and strategies A and B coexist in this interior stable equilibrium. The final state of the system converges to the asymptotically stable consensus state E3 (See Fig. 4(b)). The corresponding representative model is the snowdrift game. Therefore, when interactions between players with the payoff matrix M′ are of the coexisting-type game and the intra-group attaching bias exceeds the critical value α*, two interactive groups converge to a non-homogeneous consensus, i.e., the stable consensus state coexists with A and B.

For populations with two static topology structures, the final state converges to the interior equilibrium (, )33. For dynamic interdependent populations, the final dynamics ends at an interior equilibrium E3 which results from the co-evolution of strategy and structure. In addition, although the intra-group attaching bias α does not affect the interior equilibrium E3, it determines the stability of interior equilibrium. Only when α > α*, the interior equilibrium is stable, i.e., a too strong rewiring propensity between two interactive groups (small α) does not benefit the formation of an asymptotically stable consensus. To illustrate the effects of the intra-group attaching bias between two groups on consensus, we present the frequency of strategy A in both groups as shown in Fig. 5. We observe that for α < α*, system (6) cannot reach a consensus state (See Fig. 5(a) and Fig. 5(b)). When increasing the value of α until α > α*, system (6) reaches an asymptotically stable consensus at interior equilibrium E3. Interestingly, the increasing of α not only facilitates the formation of a consensus state in an interior equilibrium, but also enhances the speed of reaching consensus (See Fig. 5(c) and (d)). Note that the eigenvalues of the Jacobian matrix at E3 are and , respectively. Thus, increasing α means decreasing the eigenvalues of λ2, which indicates that system (6) reaches the asymptotically stable consensus state at a higher speed.

Case 3: Consensus of the bistable-type game.

When , and α > α*, both E1 and E2 are stable and E3 is unstable. Since the final state converges to E1 or E2, system (6) in the whole population is all-A or all-B, if kAA < kAB and kBB < kAB. This result indicates that all players are inclined to interact with the opponents of same strategies as themselves'.

Besides, when α < α*, E3 becomes a saddle-point, so the intra-group attaching bias α does not affect global stability of system (6). A representative model is the coordination game. In this case, strategies A and B are bistable in the interdependent populations and system (6) reaches an asymptotically stable consensus state at E1 or E2 (See Fig. 6). Note that the equilibrium, to which the system converges, depends on the initial fraction of A and the interior unstable equilibrium (, ), where . If the initial condition , system (6) converges to all-A; otherwise, to all-B. The effects of initialization on the frequency of strategy A in both groups are shown in Fig. 7. Therefore, when the interactions between players under the payoff matrix M′ are of the bistable-type game, two interactive groups converge to a homogeneous consensus state of all-A, or all-B, which relies on the initialization.

Non-weak selection

For non-weak selection intensity, the perturbation analysis does not work. Besides, the results derived under weak selection fail to extend to strong selection intensity58,62,63. Therefore, we numerically simulate to illustrate the consensus state in interdependent populations. It is shown that: when the consensus state refers to the homogeneous population with only one strategy, the intensity of selection does not change the final convergence state (See Fig. 8(a), (b) and (d)); when the consensus state refers to the non-homogeneous population with coexistent strategy, it will loses its stability under non-weak selection, which drives the two populations to non-consensus states (See Fig. 8(c)). Intuitively, the homogeneous consensus is robust for perturbations, so that very strong selection can not force the consensus being extinct. While the non-homogeneous consensus states is relatively unstable and sufficiently strong selection can force the consensus deviating from the previous consensus state. Therefore, the homogeneous consensus states in interdependent populations are robust in arbitrary selection intensity.

Figure 8
figure 8

The frequency of strategy in each groups under arbitrary selection intensity.

Each data point is averaged over 50 independent runs and in each run we set the time window as 1.5 × 104 generations to guarantee the final state converged. We set N1 = 150, N2 = 100, L1 = 6, L2 = 9, ω = 0.01. (a) a = 2, b = 1, c = 1.5, d = 0, kAA = 0.4, kAB = 0.6 and kBB = 0.8, system (4) reaches an asymptotically stable consensus state of all-A. (b) a = 1.5, b = 0, c = 2, d = 1, kAA = 0.6, kAB = 0.4 and kBB = 0.8, system (4) reaches an asymptotically stable consensus state of all-B. (c) a = 1.5, b = 1, c = 3, d = 0, kAA = 0.6, kAB = 0.4, kBB = 0.8, α = 0.7 and system (4) reaches an asymptotically stable consensus state when selection intensity is weak, which, however reaches a non-consensus state when selection is non-weak. (d) a = 2, b = 0, c = 1.5, d = 1, kAA = 0.4, kAB = 0.6, kBB = 0.8 and α = 0.7, system (4) reaches an asymptotically stable consensus of all-A.

Full size image

Discussion

To sum up, we have found that natural selection leads to stablized consensus, where the population structure is not only interdependent but also dynamical. For neutral selection, we find that consensus can always be reached, yet none of these consensus states are stable. In fact, neutral selection will drive the population from one consensus state to another from time to time. When selection is present yet weak, the two interactive groups cannot always reach a consensus state. Interestingly, once the consensus is reached, it must be asymptotically stable. Therefore, natural selection here acts as a double-edged sword: it may drive the two populations to non-consensus states, which never occurs when selection is absent; however, once consensus is established by selection, it is evolutionarily stable.

Importantly, the interdependent structure allows us to address how the intra-group attaching bias affects the stabilization of consensus. This intra-group bias is similar to the in-group bias where the structure is taken as a community. In particular, if all the individuals are only enabled to attach to individuals in the same group when adjusting their neighbourhood, i.e., under strong ingroup bias, the two interactive groups become isolated sooner or later. And each group degenerates to a non-interdependent population, which has been intensively discussed before15,16,34,35,36,37. On the other hand, allowing individuals to attach the other group yields two initially isolated groups connected. In this case, we find the intra-group attaching bias plays a major role in the convergent speed that the whole population reaches consensus.

It turns out that the consensus state strongly depends on i) what kind of conflicts they are engaging in and ii) how players adjust their partnership. In fact, the neighbourhood adjusting rules transform the local competition to other types49,50. Interestingly, this transformation can be captured by the modified matrix Eq. (3). Specially, for the modified payoff matrix with all the entries equal to each other, the evolutionary process is independent of players' payoff. This scenario can emerge even when the local competition is frequency dependent, provided the neighberhood adjusting rule is appropriate. In this case, the interaction is similar to neutral selection, there is neither good nor bad strategies and the conflicts among players degenerate to the voter model64,65. For the entry of the modified matrix Eq. (3) satisfy and , i.e., all players are apt to interact with strategy A regardless of their own strategies and the conflict in the interdependent populations become a dominant-type game. It is best to stick to dominant strategy no matter what other co-players perform and the system always reaches a consensus of homogeneous state with the dominant strategy. Similarly, for the bistable-type game, the system reaches a consensus of a homogeneous state. And it is up to the initial fraction of strategy A in each interactive-group that which homogenous state it ends up with. In the case of the coexisting-type game, the system can reach a consensus of coexistent state at an interior equilibrium and strong intra-group attaching bias not only benefits the formation of an asymptotically stable consensus, but also enhances the speed of reaching consensus. Intuitively, consensus seems to be more likely to come into being, if two groups are more likely to interact with each other. In biology, this refers to frequent gene-flow between two niches. And it is believed that convergent evolution is more likely to occur, since the environments of the two niches are similar66,67. Yet, our results highlight the importance of both the interaction between two groups and the conflict therein.

As the first stage, we simply restrict our model to two interactive groups, which is the minimum interdependent populations. For general interdependent populations with more interactive groups, the microscopic rule and analyses still work, though it can be technically tedious. What's more, based on the microscopic rule, the proposed macro-dynamics governing the frequency of the strategy in each group stands within the fast partnership rewiring process49,50,51,52, which opens an avenue via the down-to-up way to address how such co-evolutionary dynamics affects the collective behaviors in interdependent populations.