Introduction

The electronic structure of hexagonal NiS has remained a classic problem in the field of metal-insulator transition (MIT), attracting sustained interest spanning a period of several decades1,2,3,4,5,6,7,8,9,10,11,12,13. Its first order phase transition between a highly conducting (~10−5 Ω-cm) Pauli paramagnetic state at temperatures (T) greater than the transition temperature Tt ~ 265 K and an antiferromagnetic, low conductivity (~10−3 Ω-cm) state for T < 265 K is a matter of discussion in textbooks on MIT14,15,16 for many years. While every conceivable relevant experiment has been carried out with care for this system, the nature and the origin of the low temperature (LT) phase has remained inconclusive. While all investigations agree that the LT phase is a simple A type antiferromagnet, the essential difficulty in describing the LT phase arises from its unusual electronic/transport properties. The basic issue in this context is whether the LT phase of NiS, a metal or an insulator. In spite of this being an apparently simple issue to settle, a host of experimental techniques employed to address the issue of metallicity in the LT phase, have failed to resolve the controversy. For example, the low temperature resistivity6, which in itself is often a good indicator of the ground state being a metal or an insulator, is in the range of ~10−3 Ω-cm which can be described as that of a very bad/dirty metal or a poor insulator (either because of a very small gap or because of shallow impurity levels), this value of the resistivity being in the range of Mott's minimum metallic conductivity. Early measurements of the Hall resistivity of NiS established a carrier concentration of ~1020–1021/cm3, which is smaller than in good metals, but too large to be reconciled with an insulator. This would suggest NiS to be a low carrier density metal. However, it is known that NiS invariably forms with Ni deficiency, leading to a chemical formula of Ni1−xS. Hall measurements for a series of Ni1−xS with different values of x indicated that the carrier concentration is a nearly linear function of x and, more importantly, the extrapolated carrier concentration at x = 0 is very close to zero, suggesting that the stoichiometric compound is, in fact, an insulator6. Similar confusion also exists in the interpretation of the photoconductivity data which shows17 a gap-like structure with a pronounced minimum at ~180 meV followed by a small rise with further decrease in the frequency (ω). While the small but finite photoconductivity for ω → 0 can be interpreted as the signature of the Drude-peak in a bad metal, the pronounced gap like structure has been used to suggest17 NiS to be an insulator with a band gap of about 180 meV. In this latter interpretation, the Drude-like feature is thought to arise from doped carriers due to a finite concentration of Ni vacancy. Photoemission studies with its direct measurement of states at and around the Fermi energy ought to be able to resolve the controversy conclusively. However, very similar photoemission data have been used in two different publications to imply an insulating10 and a metallic ground state11, therefore, not helping to resolve the controversy. Photoemission experiments, however do establish that an energy gap, if at all existent in NiS, is not larger than a couple of meV11. This is in direct contrast to the suggestion of a gap of about 180 meV based on optical conductivity data17.

In view of such extensive and high quality experimental information available on the LT phase of NiS, the ground state of this system appears to be over-determined, making it an ideal case for theoretical investigations. There have been several theoretical attempts4,8,12,18,19,20,21 to calculate the electronic structure of the LT phase of NiS. Some of these works8,12,20,21 claim NiS to be non-metallic, while almost equal number of studies4,18,19 claim that NiS is metallic. Curiously, none of these earlier studies made use of the availability of the vast experimental information on NiS. In this report, we present the electronic structure of NiS as a function of U within the local spin density functional theory (LSDA) + U, comparing theoretical results with experimental ones and finally resolving the several decade long controversies concerning the ground state of NiS, establishing it as a novel example of a dilute, self-doped and, consequently nearly compensated p-d metal. In addition, we establish the origin of the specific magnetic structure found in the LT phase of NiS, underscoring the importance of the less discussed super-exchange interaction through ≤90° bond angle. These mechanisms being dependent solely on the geometric structure, present considerations are of relevance not only to all compounds forming in the NiAs structure, but also more generally, to any compound that contains face-sharing octahedral arrangement of the transition metal ions.

Results

In agreement with an earlier study9, our self-consistent FPLAPW spin-polarized calculations for both LT and high temperature (HT) crystal structures in the framework of LSDA do not yield an antiferromagnetic ground state and converged to non-magnetic metallic solutions. Results of our LSDA + U calculations as a function of U are shown in Fig. 1 in terms of the magnetic moment and the band gap. Thus, Fig. 1 clearly establishes a phase diagram for the ground state of NiS, showing that the ground state is a non-magnetic metal for U < 0.8 eV, an antiferromagnetic metal 0.8 eV ≤ U < 3.0 eV and an antiferromagnetic insulator for U ≥ 3.0 eV. Expectedly, the magnetic moment increases monotonously and the band gap nearly linearly with U, beyond two critical values of U, eV and eV for the magnetic transition and the metal-insulator transition, respectively. We do not stress the exact numerical values of the two Uc's, since it is known that the value of U required to reproduce experimental results within LSDA + U is in general smaller than the U estimated from constrained density functional calculations22. However we believe that the qualitative features of the phase diagram is robust.

Figure 1
figure 1

The phase diagram for the ground state of NiS as a function of U. Change of the magnetic moment per Ni site and the band gap in the antiferromagnetic phase as a function of U are also shown.

Full size image

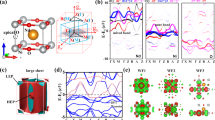
Ground state antiferromagnetic structures for both the metallic and the insulating states are found to be the same A type antiferromagnet. This is the reason why the magnetic moment does not show any anomaly across the metal-insulator boundary at Uc2 = 3.0 eV. This particular magnetic structure can be understood on the basis of the filling of Ni-d bands and the geometric structure. In the presence of octahedral crystal field splitting in the NiAs structure, the t2g states are completely occupied, while the eg states are half filled for Ni in the d8 configuration in NiS. Ni atoms along the (a,b) plane are coupled to each other with an 88° Ni-S-Ni bond angle arising from the edge-sharing octahedra. This nearly 90° superexchange interaction via the S 2p states gives rise to a weak ferromagnetic coupling, leading to the ferromagnetic arrangement of Ni atoms in the (a,b) plane. The Ni atoms in the successive planes along the c-axis are, however, connected by the face-shared NiS6 octahedra, making Ni-S-Ni bond angle to be 68°. This allows for a substantial Ni eg-S 2p-Ni eg hopping, thereby making the Ni atoms in successive planes along the c-axis coupled antiferromagnetically due to the superexchange interaction. We calculated the antiferromagnetic superexchange interaction to be quite strong (126.5 meV), based on an effective Ni-d model. This is consistent with the reported very high value of the NiS Neel temperature5.

As for the electronic structure, present calculations indicate extensive mixing of Ni d and S p states for the range of values of U (0.8 eV ≤ U < 3.0 eV) where we find the antiferromagnetic metallic phase, as shown in the Supplemental Material (SM) in terms site and orbital projected partial densities of states and fat-band representation of the energy dispersions. This establishes NiS within this range of U-values to be a p-d metal. The presence of the nearby insulating phase with increasing U confirms the correlated nature of this p-d metallic phase close to the phase boundary. It is interesting to note that an antiferromagnetic metallic phase has indeed been shown23,24 to exist within the extended Zaanen-Sawatzky-Allen type phase diagram for such inorganic solids within the p-d metallic phase adjacent to the covalent insulator phase. However, the range of interesting properties of the LT phase of NiS, established experimentally, cannot be understood within such a simplistic generic description.

We show the band dispersions along various high symmetry directions of the Brillouin zone in Fig. 2(a) and (b) for two values of U, namely 3.3 eV and 2.3 eV, corresponding to the antiferromagnetic insulating and metallic states, respectively. The essential points to note in these band dispersions are that (i) the insulating state has an indirect gap with the top of the valence band at the A (0, 0, ) point and the bottom of the conduction band at an intermediate k-point along the A-L direction; and (ii) the transition to the metallic state retains the band dispersions almost identical to that of the insulating state, with the conduction bands moving down in energy relative to the valence bands. These essential aspects can be represented by the schematic band dispersions shown in Fig. 2(c) and (d). From this schematic, it becomes obvious that the bandgap goes continuously to zero as U approaches Uc2 from above, as also seen in our calculated results (Fig. 1). As soon as U begins to be lowered below Uc2, electrons from the top of the valence band are transferred to the bottom of the conduction band (and some other k-points depending on the U-value) of the Brillouin zone, thereby a part of the d-band doping another part in the same d-manifold. This self-doping ensures that the electron and the hole volumes contained by the Fermi surface are exactly equal. This is not only true for the schematic dispersions shown in Fig. 2(d), but also for the full, all orbital calculation in Fig. 2(b), independent of all details of the full calculation such as the A point having two hole pockets and the bottom of the conduction band having only one electron pocket as can be seen in the corresponding Fermi surface plots in the SM. In this rather unexpected case of self-doping, the material may be in a nearly-compensated state, if the electron and hole mobilities are similar, as would be suggested by similar curvatures of band dispersions defining the electron and hole pockets. In the remaining part of this article, we explore the consequences of this unusual ground state electronic structure vis-a-vis the main issue of insulating/metallic ground state of NiS.

Figure 2
figure 2

Band dispersion along various high symmetry directions for (a) U = 3.3 eV and (b) 2.3 eV. Corresponding schematic diagrams are shown in (c) and (d).

Full size image

While the high resolution photoemission experiment11 clearly suggested a metallic ground state with substantial density of states at and around the Fermi energy, the strongest suggestion in favor of the insulating state has been thought to come from the gap-like structure in the optical conductivity data17, reproduced in Fig. 3(a), showing both the intraband contribution, believed to arise from Ni vacancies and the interband part, suggestive of an underlying insulating gap of stoichiometric NiS of the order of ≈ 0.2 eV. In order to make the comparison between calculated and experimental results on polycrystalline samples17, we obtain the average of the two theoretically computed inter-band components of the optical conductivity as [2 × σxx(ω) + σzz(ω)]/3. The intra-band Drude component of the optical conductivity is calculated from the bare plasma frequencies (see SM). We first choose the value of U to be 3.5 eV, such that the calculated band gap of NiS is 0.2 eV, as claimed in ref. 17. The calculated optical conductivity (Fig. 3(a)) is obviously inconsistent with the experimental result. The reason for this disagreement is quite simple to understand, though this was not appreciated before in spite of the extensive work of several decades on NiS. Associating the sharp drop in the optical conductivity with a gap in the underlying electronic structure, as interpreted in Ref. 17, is only possible for direct band gap materials, while antiferromagnetic NiS has an indirect band gap in the insulating state; we stress here that this is a robust claim and is not dependent on the specific details of any given calculation. We also show the calculated results with U = 3.0 eV, such that the band gap in the electronic structure is ≈ 0; clearly the calculated optical conductivity is still significantly shifted towards the higher energy compared to the experimental data, thereby eliminating any hope to interpret the experimentally observed optical conductivity within an insulating state. A better description of the experimental results is obtained for U = 2.3 eV (Fig. 3(a)), clearly establishing that experimental optical conductivity is consistent only with the metallic state, in sharp contrast to the exactly opposite conclusion drawn so far in the literature.

Figure 3
figure 3

Comparison of the experimental and theoretical optical conductivity of Ni0.998S as discussed in the text.

Experimental data are taken from ref. 17.

Full size image

The calculated optical conductivity for U = 2.3 eV in a larger energy window shows a feature-for-feature similarity when compared with the experimental results except that the calculated features appear systematically at increasingly higher energy. However a contraction of the energy scale by ~30% brings the calculated result in excellent agreement with the experimental data as displayed in Fig. 3(b). The necessity for the energy contraction is well-known in the literature whenever calculated spectral features are compared with experimental data involving unoccupied states, such as Bremsstrahlung Isochromat and X-ray absorption spectroscopies as illustrated in Ref. 25. The need for this contraction may arise from limitations of density functional theories in describing the unoccupied states. Another reason can be the neglect of the electron-hole Coulomb interaction in obtaining the calculated results, while the experimental result is invariably influenced by such interactions.

We have also carried out additional electronic structure calculations for NiS using range of new techniques (e.g. G0W0, scGW0 and scGW) (see SM) and find that the essential features of the antiferromagnetic state, discussed above are independent of the calculation scheme adopted, establishing the validity and the robustness of our conclusion. While this reinterpretation of the optical conductivity data in conjunction with the high resolution photoemission results11 suffice to establish the ground state of the antiferromagnetic NiS to be metallic, we further require that the present calculation be consistent with other known experimental results from the LT phase of NiS, thereby providing further credence to the unusual metallic ground state of NiS described here. In doing so, we fix the value of U at 2.3 eV, as suggested by the comparison in Fig. 3(a).

Based on our results on stoichiometric NiS, we compute the Hall coefficient (RH) and resistivity(ρ) in the frame work of Boltzmann transport theory (details in the SM) as a function of the Ni vacancy x, where the introduction of holes via Ni vacancy is modeled by the rigid band approximation. In addition to the carrier concentration, we have evaluated effective carrier masses , and , associated with the electron, light hole and heavy hole carriers. Fig. 4 shows a comparison of the theoretically calculated Hall resistivity (RH) of Ni1−xS as a function of x compared with the experimentally obtained results. If we scale the computed values by a single constant ( = 3.4) to match the experimental value at one point, say x = 0.01, we find a near perfect match between the calculated and experimental RH(x) for all other compositions. Thus, present results are able to describe the dependence of RH on x exceedingly well with a quantitative agreement well within an order of magnitude of experimental values, thereby establishing a remarkable success of the description of NiS as a self-doped, nearly compensated antiferromagnetic metal.

Figure 4
figure 4

Comparison of experimental (filled circles), calculated (solid line) and scaled calculated values (dashed line) for Hall coefficient as a function of Ni vacancy (x).

Experimental data are from ref. 6. The inset shows the same for the resistivity.

Full size image

We note that the mobility is experimentally obtained as a ratio between the RH and the resistivity, ρ, as in ref. 6. Thus, the scaled, calculated RH in conjunction with the experimentally obtained mobility from ref. 6 is bound to provide a very good description of the resistivity as a function of x as well. Going beyond this obvious point, we estimate the mobilities of different charge-carriers at different x-values based on our calculations, as detailed in SM, instead of taking them from experimental results. We note that the mobility is inversely proportional to the effective mass of a band. We adjust this proportionality constant to equate the computed resistivity with experimentally observed value for x = 0.01 and then use the same constant to compute the mobility and, therefore, the resistivity of all other compositions without any adjustable parameter. The resulting calculated resistivity as a function of x is shown in the inset to Fig. 4 compared to the experimental data, exhibiting a good match at all compositions except for the lowest x value. We note that a slightly incorrect estimation of the experimental x value at this composition can easily account for the discrepancy, since the resistivity rises sharply in this x regime with decreasing x.

We now address the experimentally observed nonmagnetic-antiferromagnetic metal-to-metal transition in NiS across Tc = 265 K. Within our approach, this requires a substantial change in the value of the intra-atomic Coulomb interaction strength (U) in the order of at least 1.5 eV between the two phases, as evident in Fig. 1. In order to understand such a substantial change in the strength of the intra-atomic Coulomb interaction between the two states, we have computed the value of U self-consistently within the constrained random-phase approximation26,27. For the HT crystal structure we obtain U = 1.8 eV and for the LT antiferromagnetic state U = 3.7 eV. While these values by themselves would suggest incorrect electronic structures for both phases according to Fig. 1, for example a magnetic state for the HT structure, we note the known underestimation of U values obtained by requiring the right ground state properties within LSDA + U compared to the one obtained from such constrained approaches22. Instead it is important to note here that significantly, we find an appreciable increase of about 1.9 eV in the calculated strength of U in going from the nonmagnetic to the antiferromagnetic state, as also suggested by our analysis of the experimental data in terms of LSDA + U approach presented in this work. This increase in U in going from the nonmagnetic state to the antiferromagnetic state can be easily understood in terms of its dependence on the magnetic moment. In antiferromagnets, a shift of the spectral-weight around the Fermi level reduces the DOS, which leads to smaller polarization and thus, to larger U values. Larger the magnetic moment stronger becomes the Coulomb interaction strength, U.

Finally we show the density of states obtained for the self-doped, antiferromagnetic metallic phase with U = 2.3 eV and that for the nonmagnetic metallic phase in Fig. 5. While the two DOS are roughly similar, we can clearly see two distinctive changes that should be visible in photoemission experiments. First is the small movement of the most intense part of the DOS near 2 eV towards a higher binding energy in the self-doped, antiferromagnetic metallic state. This is in agreement with a similar shift of the main photoemission peak reported for the LT phase of NiS in ref. 10. The other visible change is a depletion of the DOS at EF for the self-doped antiferromagnetic state compared to the nonmagnetic one. This is exactly what has been reported in ref. 11, with experimental photoemission data showing a decrease in the spectral weight at EF, though it remains finite, at the lowest temperature. The decrease in the DOS is related to a decrease in the Fermi volume in the LT phase, associated with opening of gaps at the Fermi energy along several momentum directions.

Figure 5
figure 5

Total DOS corresponding to the AFM and NM phase for U = 2.3 eV.

The energy scale is referenced to the Fermi energy.

Full size image

Discussion

We have shown that the LT phase of NiS in the NiAs structure has to be described as a novel self-doped, nearly compensated antiferromagnetic metal close to the p-d metal/covalent insulator phase line. A host of physical properties calculated on the basis of this description of the ground state of NiS is in remarkable agreement with all experimentally determined properties of NiS, establishing the much discussed temperature driven phase transition of NiS at about 265 K to be one between a Pauli paramagnetic metal and this unusual self doped antiferromagnetic metal. We have also shown that the transition from the HT nonmagnetic metallic state to the LT antiferromagnetic unusual metal state is driven by a substantial increase in the intra-atomic Coulomb interaction strength, that remains sub-critical to drive the system in to an insulating state.

Methods

All calculations reported in this work are carried out using full potential linearized augmented plane wave (FPLAPW) plus local orbitals method as embodied in WIEN2k code28. The muffin-tin radii (RMT) of Ni and S are chosen to be 1.23 Å. and 1.09 Å, respectively. To achieve energy convergence of the eigenvalues, the wave functions in the interstitial region were expanded in plane waves with a cutoff RMTkmax = 7, where RMT denotes the smallest atomic sphere radius and kmax represents the magnitude of the largest k vector in the plane wave expansion. The valence wave functions inside the spheres are expanded up to lmax = 10, while the charge density was Fourier expanded up to Gmax = 12. The Brillouin-zone integration was performed with a modified tetrahedron method using 394 and 2839 special k points in the irreducible part of the Brillouin-zone to achieve self-consistency and for optical calculations, respectively. Exchange and correlation effects are treated within the DFT using LSDA29 and a Hubbard U was included in the framework30 of LSDA + U for the description of electron correlations. Hexagonal NiS crystallizes in the NiAs structure31. Since we are interested in the ground state of NiS, all results reported here are for the LT structure, unless otherwise stated.