Introduction

The need to control is ubiquitous in many complex systems. For example, a cellular system controls a series of chemical reactions during its division to guarantee sufficient genetic materials in each daughter cell1,2,3. A company controls the dynamics of information flow for efficient task execution or innovation4. In a supply chain, cost is reduced by controlling the commodity flow5. Therefore there is an increasing need to understand the control principles of complex systems.

Recent advances in applying control theory6,7,8 to complex networks9,10 shed new light on this problem11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28. According to control theory, a dynamical system is controllable if it can be driven from any initial state to any desired final state within finite time6,7. Obviously, when we influence every element in the system, we obtain full control. However, control in general can be achieved through the control of only a subset of nodes that we call driver nodes. In a linear time-invariant system, the minimum driver node set (MDS) can be efficiently identified, representing the minimum set of nodes through which we can yield control over the whole system12. It has been shown that the number of driver nodes necessary for control (ND) is fixed in a given network and primarily determined by the underlying degree distribution. Yet, there are often multiple control configurations with the same ND24. For example, in the six-node network shown in Fig. 1a ND = 4, but control can be achieved via five different MDS's: {1, 2, 4, 6}, {1, 2, 4, 5}, {1, 2, 3, 6}, {1, 2, 3, 5} and {1, 2, 3, 4}.

Figure 1
figure 1

(a) An example of a directed network with six nodes. (b) The bipartite representation of the directed network in (a) where nodes are represented as two disjoint sets of nodes out and in. A directed link from node 1 to node 3 in (a) corresponds to a connection between node 1 in the out set and node 3 in the in set. (c) One maximum matching configuration of the bipartite graph (b) where one node can maximumly match another node through one link. Colored nodes and links are matched nodes and links respectively. (d) One choice of minimum driver node set (MDS) to control the network based on the maximum matching in (c), i.e. controlling nodes 1, 2, 4 and 6 to control the whole system.

Full size image

The existence of multiple MDS's indicates that not all nodes participate in control equiprobability, prompting us to quantify the role of each node in control. Here we introduce the concept of control capacity φ(i), defined as the fraction of MDS's in which node i is included. This quantity measures the participation of node i in MDS's, hence gives the likelihood that node i is a driver node when the network is under control via a random control configuration. For example, in Fig. 1a, the control capacity of each node is φ(1) = φ(2) = 1, φ(3) = φ(4) = 0.6 and φ(5) = φ(6) = 0.4. In connection with previous work that classifies nodes into three categories24, a node with φ = 1 is critical as it always acts as a driver node, φ = 0 is redundant as it never participates in MDS's whereas 0 < φ < 1 is intermittent as it plays as a driver node in some control configurations but not all.

In spite of its direct relevance control capacity is difficult to measure, as only nodes with φ = 0 and φ = 1 can be identified in polynomial time24. Intuitively control capacity is readily obtained once all MDS's are known. However, enumeration of all MDS's in an arbitrary network is in the class of #P problem and computationally prohibitive for large networks. Indeed, the number of MDS's can grow exponentially with networks size, hence a network with only hundreds of nodes often leads to millions of MDS's29. To cope with this difficulty we propose a random sampling algorithm, allowing us to measure the control capacity within a limited number of MDS's, drawn randomly from all MDS's. In the following we show that our algorithm yields a random pick of MDS and provides reliable statistical estimation of control capacity of nodes in arbitrary networks.

Results

Random sampling algorithm

We start by briefly reviewing the process in identifying ND and MDS for an arbitrary directed network. First, a directed network is converted to a bipartite graph with two disjoint sets of nodes out and in. The out nodes can be considered as “superiors” that influence others internally. The in nodes are “subordinates” that need to be controlled. A directed link from node i to j corresponds to a connection between node i in the out set and node j in the in set in the bipartite graph (Fig. 1a, b). By performing the maximum matching in the bipartite graph12,30, the minimum driver nodes are unmatched nodes in the in set (Fig. 1c, d).

The method provides a direct connection between a maximumly-matched set (MMS) and a MDS, as the complementary set of a MMS yields a MDS. One can use different algorithms to find the maximum matching in a bipartite graph, such as Hopcroft-Karp algorithm30, FordFulkerson algorithm31 and Hungarian algorithm32. All these algorithms aim to increase the matching size in each iteration via the augmenting path that starts at a matched node, end on a unmatched node and alternates between unmatched and matched links on the path17. Because there is no randomness in identifying an augmenting path, these algorithms will locate only one MMS for a given initial condition hence they are not appropriate for sampling purposes. Two simple modifications can be applied to bring randomness: one is to randomize the initial matching and the other is to randomly choose possible augmenting paths. However, sampling based on these methods are not guaranteed to be uniform among all MMS's and can be typically biased.

Here we propose a novel algorithm that performs unbiased random sampling among all MMS's, which equivalently samples all MDS's and estimates the control capacity. The steps are as follows: 0. For simplicity, remove the always matched nodes in the in set and their links (the algorithm to identify always matched nodes is introduced in reference24). Denote by G the bipartite graph obtained after node removal.

  1. 1

    Obtain one MMS (denoted by M).

  2. 2

    Randomly pick an element in M (denoted by node i).

  3. 3

    Enumerate all alternative MMS's that include all other elements of M except node i. (see Methods)

  4. 4

    Randomly pick one of these alternative MMS as the current MMS M.

  5. 5

    Repeat step 2.

Now we prove that the above steps randomly samples MMS's. Considering each MMS as one state, our algorithm maps to a Markov chain characterized by a transition matrix P with the element pi,j that equals the probability of transition from state i to j. Without loosing generality, assume two MMS as sets of m nodes {n1, n2, …, na, …, nm} and {n1, n2, …, nb, …, nm}, denoted by M1 and M2 respectively. Suppose that there are totally z other MMS's that include n1, n2, …, nm except na or nb and consider the MMS M1 and M2 as two state i and j in the Markov chain that our algorithm maps to. The transition from state i to j requires the pick of element na out of m elements with probability 1/m and the pick of set M2 out of z + 1 alternative sets with probability 1/(z + 1). Therefore . Similarly, from state j to i, the probability to pick element nb is 1/m. As the number of alternative MMS's including n1, n2, …, nN except nb is also z + 1, . Hence pi,j = pj,i and the transition matrix P is symmetric. For Markov chain with symmetric transition matrix, the steady state distribution is with equal probabilities for all states33. This means that in the long run, each MMS is picked with the same probability as all others.

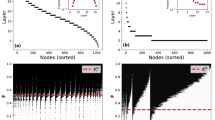
To verify the result, we construct a small network with 244 MDS's, perform our sampling algorithm 48,800 iterations and count the time that each MDS is picked. We find that each MDS is sampled approximately 200 times (Fig. 2a), which is the expected count a random sampling yields. The distribution of the counts follows a Gaussian distribution (Fig. 2b) centered at 200, implying the difference between actual and expected counts are due to random fluctuation.

Figure 2
figure 2

(a) The count on each of 244 MDS's is around the expected value 200 when taking 48800 samples. (b) The distribution of the counts that is centered at 200 and can be well fitted by a Gaussian distribution. (c) The time evolution of φt(i)/φ(i) of 33 nodes with 0 < φ < 1. φt(i) is the control capacity of node i at time-step t based on the samples collected up to t and φ(i) is the expected control capacity of node i that is explicitly measured through the enumeration of all 153,123 MDS's. Control capacity starts to converge at the characteristic time-step T. (d) The time evolution of the mean absolute percentage error MAPE = Σi|φt(i) − φ(i)|/n, where n is the number of nodes with 0 < φ < 1. MAPE drops quickly after T time-steps.

Full size image

One important attribute of a sampling method is the rate of convergence, capturing how fast the estimate converges to the actual value. Typically the rate of convergence is not known exactly unless an analytical solution can be found for the sampling process34. Via numerical tests, we find that the sampling results converges to the actual value after T = N ln N iterations in a network with N nodes. The interpretation of T is intuitive: as our algorithm randomly draws the original elements in the MMS and replaces it with the new ones, the measure will not converge until we have the original MMS completely shuffled. Assuming that the size of the MMS is m, the expected number of iterations to obtain the first element replaced is 1, second element replaced is m/(m − 1) and the nth element replaced is m/(m − n). Therefore for m elements the expected iteration is . As m varies but is proportional to network size N, we replace m by N and hence have the characteristic time-step T.

The characteristic time-step provides the minimum number of iterations necessary for sampling, therefore capturing the complexity in quantifying control capacity. The time needed to find one maximum matching can be as small as with the Hopcroft-Karp algorithm in a network with N nodes and L links30. To find one alternative MMS with one node replaced, a breadth first search is needed with time. As the number of alternative MMS is capped by N, the complexity of one sampling is . As the sampling time needed is proportional to T, the control capacity can be estimated in polynomial time as .

To test our proposition, we construct a network with 100 nodes. We explicitly enumerate all 153,123 MDS's (see Methods) and exactly measure the control capacity of all 33 nodes with 0 < φ < 1. Then we apply the random sampling and estimate the capacity φt(i) of each node i at time-step t based on the samples collected up to t. It is observed that φt(i) quickly converges to the expected value in T = N ln N steps (Fig. 2c,d). It is also noteworthy that in 3000 iterations, which cover fewer than 2% of all MDS's, the mean absolute percentage error (MAPE) of the estimated control capacity is less than 3% (Fig. 2d), indicating the efficiency of utilizing random sampling in estimating the control capacity that significantly reduces the computational complexity.

Control capacity in model and real networks

We check the relationship between a node's topological property and its role in control. On the one hand, we find that a node's out-degree does not affect its control capacity (Fig. 3b). This is because the outgoing links serve as means to control other nodes, which does not affect how this node itself would be controlled. On the other hand, control capacity does depend on in-degree. Particularly φ = 1 when kin = 0, indicating that nodes without incoming links need to be always controlled, in line with our previous finding24. As in-degree increases, φ decays rapidly (Fig. 3a), indicating that a node with more incoming links are less likely to be a driver node as they are more likely to be influenced internally.

Figure 3
figure 3

Dependency between control capacity φ and nodes' in- and out-degree.

(a) φ decays rapidly with in-degree kin, suggesting that nodes with more incoming links are less likely to be a driver node. φ = 0 when kin = 0, indicating that nodes without incoming links are always driver nodes. (b) For the same networks in (a), φ does not vary with out-degree kout, indicating control capacity is independent of out-degree. Networks analyzed are generated by static model (see Methods) with size N = 10,000 where , , γin = γout = γ and .

Full size image

We extend the analysis to real systems and check the relationship between 〈kD〉 and 〈k〉, which are the average degree of the driver nodes and all nodes, respectively (Table 1). With control capacity, 〈kD〉 can be explicitly expressed as 〈kD〉 = Σiφ(i)k(i)/ND where k(i) is the degree of an arbitrary node i. One would expect 〈kD〉 < 〈k〉 in real networks since φ decreases with kin. However, while the fact that the average in-degree of driver nodes is less than that of the network (〈kD,in〉 < 〈kin〉) reflects the relationship between φ and kin, average out-degree of driver nodes (〈kD,out〉) can be affected by the in- and out-degree correlation21,35,36,37,38 featuring in real systems and the finite size effect39,40. Indeed several networks are found with 〈kD,out〉 > 〈kout〉 (e.g. Seagrass in food web and TRN-Yeast-2 in regulatory networks of Table 1) and in one network we even observe that 〈kD〉 is slightly higher than 〈k〉 (TRN-EC-2 in regulatory networks of Table 1). But for majority of real networks the average degree of driver nodes are less than that of the whole network, leading to the conclusion that hubs are less likely to be driver nodes12.

Table 1 Real networks Analyzed. For each network, we show its type, name; number of nodes (N) and links (L); average degree 〈k〉; average degree of driver nodes 〈kD〉 and average in- and out-degree of driver nodes (〈kD,in〉 and 〈kD,out〉), respectively
Full size table

Finally, we check how control capacity is distributed among nodes with 0 < φ < 1 in Erdös-Rényi networks41, scale-free networks42 (see Methods) and some real networks (Fig. 4). The distributions are found to depend on specific network configurations and there seems no simple universal function for the distribution. But as a common feature, φ typically displays multi-modal distribution, implying that several clusters of nodes share about the same chance of being driver nodes. Recent work24 discovered that dense networks with identical degree distribution can stay in one of the two control modes, centralized or distributed, depending on the fraction of nodes that can participate in MDS's. The distributions of control capacity corresponding to networks in the two control modes also show distinct features. For networks in distributed mode, a significant fraction of nodes are with control capacity close to zero (Fig. 4(b), (e)). This indicates that while many nodes can participate in MDS's, their participation is not frequent compared with the huge number of MDS's in distributed mode. For networks in centralized mode, the number of nodes with 0 < φ < 1 is small, but the distribution of capacity among these nodes is similar to that when 〈k〉 is small (Fig. 4(c), (f)).

Figure 4
figure 4

Distribution of control capacity φ among nodes with 0 < φ < 1 in Erdős-Rényi networks ((a)–(c)), scale-free networks ((d)–(f)) and real networks ((g)–(i)).

Dense networks with identical degree distribution in centralized ((c) and (f)) and distributed ((b) and (e)) control modes are labeled. For Erdős-Rényi and scale-free networks, network size N = 10,000. For scale-free networks, γin = γout = 3. The information for the three real networks is listed in Table 1.

Full size image

Discussion

In summary, uncovering the role of individual nodes in controlling a network requires us to understand control capacity, a centrality measure quantifying a node's likelihood of being a driver node. While a network's control can be achieved via different MDS's and each may give rise to different outcomes, we lack a tool to average the effect of different MDS's or statistically analyze the consequences driven by different MDS's over the network. In this paper we propose a random sampling algorithm, allowing us to efficiently measure control capacity in arbitrary networks. The proposed algorithm bridges the gap between multiple microscopic control configurations and macroscopic properties of the network under control. One important example of its application is the study of 〈kD〉, which can not be properly addressed without the random sampling method12.

The results presented have many potential applications in future works. For example, recent work on the controllability of bank systems investigated the time correlation of nodes' roles in control25,27. The measure of control capacity could be crucial in such tasks, especially in temporal networks where a node's role in control varies with time43,44,45. The relationship between control capacity and the efficiency or energy cost in control15,28 are also important issues for further investigations. The random sampling method is useful in problems when an overall measure of a network is needed. As an example, when estimating the control robustness of a network, the random sampling algorithm has to be considered as different MDS's may facing different failure risks. Finally, links do not participate in control in an equal manner, allowing multiple link combinations to spread the control signal. Our approach can offer insights for future work exploring the participation of links in control. Given the inherent multiplicity feature in control, our findings offer fundamental tools to explore control in various complex systems.

Methods

Enumerating all alternative MMS's with one node replaced

Suppose the maximum matching is obtained in a bipartite graph and denote M by the current maximumly-matched set (MMS) of nodes in the in set. Assume node i is an element of the set M. The following procedures can provide all MMS's that contain all other elements of M except node i. (0) Set node i as the removal node. (1) Identify the node in the out set that matches the removal node (denoted by node j). (2) Keep the current matched nodes and links unchanged, remove the removal node with all its links. (3) Check if there is an augmenting path that starts from node j, ends at an unmatched node and alternates between unmatched and matched links on the path. (4) If so, we obtain a new MMS with node i replaced. Update the matched links and nodes correspondingly. Set the new matched node in the in set as the removal node and repeat step (1). (5) If not, there is no new MMS with node i replaced and all of them are enumerated already.

Enumerating all MDS's

For a given bipartite graph, we first remove all the always matched nodes in the in set and their links (algorithm discussed in reference24). Define Si as a set of nodes that a out node i can reach. For example, in Fig. 1b there are S1 = {3, 4, 5, 6} and S2 = {5, 6}. Effectively Si is the set of nodes that node i can match. In the bipartite graph with no always matched nodes in the in set, a MMS of in nodes is a set of nodes without duplication, each drawn from one set S. Therefore, we can repeatedly test all possible combinations to enumerate all MMS's that equivalently provides all MDS's. Note that nodes chosen from different S's can sometimes give rise to the same MMS. For example, in Fig. 1b picking node 5 from S1 and node 6 from S2 yields the same MMS as picking node 6 from S1 and node 5 from S2. All MMS's need to be recored. Once a valid node combination is found, it needs to be checked with previously found MMS to avoid double count.

Generating a scale free network

The scale-free networks42 analyzed are generated via the static model46. We start from N disconnected nodes indexed by integer number i (i = 1, … N). The weight is assigned to each node in the out and the in set, with αout,in a real number in the range [0, 1). Randomly selected two nodes i and j respectively from the out set and the in set, with probability proportional to and . Connect node i and j if there is no connection between them, corresponding to a directed link from node i to node j in the digraph. Otherwise randomly choose another pair. Repeated the procedure until 〈kin〉 = 〈kout〉 = 〈k〉/2 links are created. The degree distribution under this construction is in the large k limit.