Introduction

Slow-light chips are believed to be promising for enhanced optical buffering, signal processing and enhanced nonlinear optics. Unfortunately, the observation of slow light in conventional schemes based on Bose-Einstein condensates1 or atomic vapors2 imposes severe constraints in experimental conditions, including narrow bandwidth, limited working wavelengths and strong temperature dependence. The slowed modes are difficult to be implemented into other materials or devices to develop practical applications. Consequently, solid-state nanophotonic structures that can achieve the slow light effect under room temperature are of particular interest3,4,5. Recent theoretical and experimental investigations on the “trapped rainbow” storage of light waves in metamaterials6 and plasmonic structures7,8,9,10 have generated considerable interest since various solid-state materials can be introduced in the design of nanostructures to trap electromagnetic (EM) modes. With the ability to produce highly confined and localized optical fields, it is believed that the conventional rules for light-matter interactions need to be re-examined and new regimes of optical physics are expected. To develop applications based on this intriguing broadband slow light effect, various architectures have been proposed, including surface graded metallic gratings9,10, insulator-negative-index-insulator (INI)6,11, insulator-metal-insulator (IMI)12 and metal-insulator-metal (MIM) waveguide tapers13,14,15. However, each proposal has its inherent difficulties resulting in the limited experimental realization of the rainbow trapping structures. For example, in our previous experimental reports, white light surface plasmon polariton (SPP) modes were launched into the on-chip gratings through nanoslits9,10, leading to a very weak total coupling efficiency. For INI waveguide tapers, there is currently no clear pathway for realizing materials with negative refractive indices over a broad spectral range6. In a recent theoretical investigation, the rainbow trapping performance of INI, IMI and MIM waveguide tapers were analyzed and compared15. It was concluded that the MIM structure can trap the first order (and higher order) transverse magnetic (TM) modes which makes them the best practical candidate for rainbow trapping among the three tapered waveguide structures (i.e. INI, IMI and MIM). However, even for the MIM structure, there are theoretical constraints to achieve the rainbow trapping conditions15. Consequently, trapped “rainbow” schemes based on INI, IMI or MIM waveguide tapers remain largely in the theoretical domain due to intrinsic constraints and difficulties in fabrication. In this Letter, we propose a hyperbolic metamaterial (HMM) structure to realize a highly efficient rainbow trapping effect in the vertical direction, which, importantly, is not limited by those severe theoretical constraints required by INI, IMI and MIM waveguide tapers and therefore representing a significant promise to realize the rainbow trapping structure practically. This vertical HMM design is amenable to large area nanofabrication technologies and will enable applications based on efficient rainbow trapping including photon harvesting and enhanced on-chip light-matter interactions.

HMM is referred to an artificial medium with subwavelength features whose iso-frequency surface is a hyperboloiod16,17,18,19,20. For such a metamaterial with a diagonal form of the permittivity tensor, ε = diag(εx, εy, εz), its diagonal elements have different signs (i.e. εx < 0, εz > 0), leading to the hyperbolic iso-frequency surface, i.e. 16,17. Intriguingly, the photonic density of states in this kind of HMM is infinite due to the open (hyperboloid) iso-frequency surface18. Therefore, it is also called indefinite medium16, which is promising for a variety of new applications including three-dimensional indefinite cavities21, spontaneous emission enhancement19 and active nanoplasmonic devices22, etc. In this work, we will employ an HMM constructed by alternating metal-dielectric multi-layers to design a tapered waveguide structure for efficient and practical rainbow trapping.

Results

Effective medium theory model

To explain the fundamental mechanism, we analyze the waveguide modes supported in an air/HMM/air planar waveguide by solving the eigenequation analytically based on the effective medium theory. Considering an HMM waveguide in the inset of Figure 1a with a dielectric cladding layer (ε1 = 1) and an anisotropic core layer (e.g. ε2x = −25 + 0.25i, ε2z = 5 + 0.05i), the propagation constant β of the transverse-magnetic (TM) modes can be obtained by solving Eq. (1),

Figure 1
figure 1

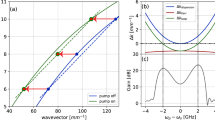
Light trapping in a lossless HMM waveguide taper.

(a) Propagation constants of TM0, TM1 and TM2 modes, β, as a function of the HMM waveguide width. The two branches for each mode are separated by a degeneracy point, represented by empty circles. (b) Normalized power flows of TM0, TM1 and TM2 modes, Pnorm, as a function of the HMM waveguide width. (c) shows |E|-field distribution of TM0, TM1 and TM2 modes in HMM waveguide tapers. In the length of 3λ along the z-direction, the tapered width increases from 0.1λ to 0.22λ in the upper panel, from 0.3λ to 0.42λ in the middle panel and from 0.55λ to 0.62λ in the lower panel, respectively.

Full size image

where , . kω = ω/c is the vacuum wave vector, w is the width of the core layer and μ is the permeability (for nonmagnetic materials, μ = 1). Here we first analyze the lossless case by neglecting the imaginary part of the permittivity of the HMM core layer, i.e. ε2x = −25, ε2z = 5. Using Eq. (1), the geometric dispersion curves of TM0, TM1 and TM2 modes are plotted in Figure 1a. One can see that an HMM core layer with a given width can support two different propagation constants for each TM mode. As the core layer width increases, a degeneracy point can be obtained as indicated by empty circles. To distinguish the optical properties of these two modes with different propagation constants, we calculate the normalized power flow in Figure 1b, i.e. where Sz is the z-component of the Poynting vector. For modes with smaller propagation constants below degeneracy points in Figure 1a (see solid lines), the power flow is parallel to the propagation direction, i.e. P > 0 as plotted by solid lines in Figure 1b (defined as the |f > mode); while for modes with larger propagation constants above degeneracy points shown in Figure 1a (see dotted lines), the power flow is anti-parallel to the propagating direction, i.e. P < 0 as plotted by dotted lines in Figure 1b (defined as the |b > mode). One can see that these two modes are getting close to each other and finally degenerate as the width of the core layer increases, which is similar to the TM0 mode behavior in IMI waveguide (when |εcore| < εcladding)14. Interestingly, at the degeneracy point (see empty circles), Pnorm is 0 indicating that these TM modes are trapped in the proposed HMM waveguide structure. To validate this prediction, we then model the electric-field (|E|-field) distribution guided in a tapered HMM waveguide using finite element method (FEM). In the numerical simulation shown in Figure 1c, the guided TM0, TM1 and TM2 modes are directly launched into the waveguide taper from the narrow end. For instance, the core layer width of the narrow end is 0.1λ in the upper panel of Figure 1c, corresponding to two propagation constants of 1.077 kω and 9.180 kω for the TM0 mode in Figure 1a. Since the smaller β (i.e. 1.077 kω) is very close to the vacuum wave vector, kω, it should be easy to launch the |f > mode practically using a free-space beam. As the |f > mode is guided along the waveguide taper with an increasing width, it will be finally trapped at the degeneracy point (i.e. w = 0.173λ, indicated by white arrows in Figure 1c), agreeing very well with the FEM modeling. Similarly, |f > modes for TM1 and TM2 modes cannot propagate beyond their corresponding degeneracy points at w = 0.380λ and 0.591λ, as show in the middle and lower panels of Figure 1c, respectively. Due to the power flow of the modes decreases to 0, the incident energy is trapped at these degeneracy points. In addition, the tangent line at the degeneracy point is parallel to the vertical direction, indicating that the group velocity is zero (see Section 1 in the supplementary information) and therefore reveals an encouraging promise to realize rainbow trapping in these HMM waveguide tapers.

In previously reported simulation results exploring the feasibility of realizing rainbow trapping in INI, IMI and MIM waveguide tapers12,13,14,15, a rainbow trapping condition parameter for having the degeneracy point, σε = |εcore/εcladding|, has been analyzed and compared. According to ref. 15, this condition for the relatively practical MIM waveguide taper structure is still challenging (e.g. for TM1: 1 < σε < 1.3510), which requires a very large permittivity of the dielectric core layer (e.g. GaP) so that the rainbow trapping can be realized in a very limited spectral range for TM1 modes. It will be demonstrated that the proposed HMM waveguide structure is not limited by these severe theoretical constraints required by INI, IMI and MIM waveguide tapers. Here we first define three parameters, , U = wγ2/2 and , to simplify the characteristic Eq. (1) as follows:

In this equation, V and σ are constants for a given waveguide structure. U is related to the propagation constant of the waveguide mode. The solution to this equation can be obtained by graphically determining the intersection points between curves of W = tanU or W = −cotU (i.e. the term on the right-hand side of Eq. (2)) and (i.e. the term on the left-hand side of Eq. (2)) in the (U, W) space (see Section 2 in the supplementary information). Based on this graphical analysis, conditions for supporting |f> and |b> branches of TM0, TM1 and TM2 modes are listed in Table 1. Particularly, the TM1 and TM2 |f> modes exist in the ranges of π/2 ≤ V ≤ V1 and π ≤ V ≤ V2, respectively, corresponding to ranges from cutoff points for TM1 and TM2 modes (indicated by arrows in Figure 1a) to their degeneracy points. In order to realize the rainbow trapping for a given wavelength, degeneracy points have to be realized, which can be met by tuning the core layer width (w) of the HMM waveguide. Consequently, as the incident TM0 mode propagates along the HMM waveguide taper from the narrow end to the broad end, the |f> and |b> modes will get close to each other and degenerate finally, as shown by the black arrow in Supplementary Fig. S1. Noticeably, during this process, only the hyperbolic condition (i.e. ε2x < 0, ε2z > 0) of the core layer is needed. Any reported metamaterials with hyperbolic iso-frequency surfaces (e.g.16,17,18,19,20) can be used to enable the degeneracy condition and therefore representing a significant promise to realize the rainbow trapping practically.

Table 1 Conditions for existence of TM0, TM1 and TM2 modes in the HMM waveguide. Consider that the corresponding thickness of the HMM core layer to support |f> and |b> modes can therefore be determined. For instance, when ε1 = 1, ε2x = −25, ε2z = 5, the thickness of the core layer is w/λ = 0.14 V. Therefore, one can control the value of V to support different TM modes by choosing the value of w/λ. At the degeneracy conditions for different order TM modes, V0 = 1.24, V1 = 2.72 and V2 = 4.23. Consequently, when w = 0.1λ, V≈0.714 indicating the existence of TM0 |f> and |b> modes, TM1 |b> and TM2 |b> modes in this HMM waveguide. When w = 0.2λ, V≈1.429 indicating the existence of TM1 |b> and TM2 |b> modes only.
Full size table

In the discussion presented above, the loss of the HMM material was neglected. This ideal but impractical assumption was usually employed to approximately predict optical behaviors of plasmonic structures and metamaterials. For example, the metal loss was neglected in previous theoretical designs of trapped rainbow of THz waves in metamaterial5 and plasmonic surface grating structures6, which resulted in a debate on the feasibility of the proposed “stop” light effect23,24. In recent years, singularities of two-crescent/kissing cylinder structures were exploited, where the singularity point is never reached in a finite time since the mode conversion will not occur under the ideal adiabaticity condition with perfect smooth interfaces and uniform incident electric-field illumination25. Many simulation results have shown that adiabatic metallic metamaterials or plasmonic structures usually do not permit the complete “stopping” of light waves in the presence of degeneracy points even under the assumption of lossless materials due to the fundamental nonadiabaticity near the degeneracy point15. More specifically, the adiabaticity condition for the graded core width variation26, dw/dz < < wkωΔn/π where Δn is the effective index difference between eigenmodes (i.e. |f > and |b > modes), cannot be met at the degeneracy point since Δn = 0. However, this criterion was still omitted occasionally in recent theoretical designs27. It should be noted that a complete stop of light is also not achievable in the lossless HMM waveguide tapers either, although the group velocity at the degeneracy point is 0 in principle. The incident |f > mode will convert to |b> mode and escape from the “trapped” position. In the next paragraph, we will consider the loss of HMM materials to explore this mode conversion process and further evaluate the rainbow trapping performance.

To reveal the difference by considering the absorption (i.e. ε2x = −25 + 0.25i, ε2z = 5 + 0.05i in our modeling), we plot the real and imaginary parts of the propagation constants, βr and βi, as shown in Figures 2a and 2b, respectively. One can see from Figure 2a that the absorption breaks the degeneracy point connecting |f> and |b> modes in the lossless case. The geometric dispersion curve for TM0 modes will extend to the right side of the lossless degeneracy point with a significantly larger loss as shown in Figure 2b. The TM0 mode behaves as an evanescent wave in this “cutoff” region, due to the large attenuation coefficient which is defined as βi/kω. On the other hand, the propagation loss for the |b> mode is much larger than that of the |f> mode, revealing a key difference before and after the mode conversion. To further evaluate the field confinement, the effective modal area is defined by , as plotted in Figure 2c. Generally, the |b> mode indicated by the dotted line has a smaller modal area than the |f> mode indicated by the solid line. The model areas of these two eigenmodes match approximately near the degeneracy point as the mode conversion occurs. To reveal the behavior of the mode propagation in the tapered lossy HMM waveguide, we perform the FEM simulation in Figure 2d. One can see that the incident |f> mode cannot propagate beyond the degeneracy point position indicated by the vertical dotted line. An obvious oscillation field distribution is observed which is mainly due to the interference between the incident |f> and reflected |b> modes (see Section 3 of the supplementary information).

Figure 2
figure 2

Light trapping in a lossy HMM waveguide taper.

The width-dependence of (a) the real part of the propagation constant, βr, (b) the attenuation coefficient, βi and (c) the effective modal area of the fundamental mode (TM0) in the lossy HMM waveguide taper. (d) The |E|-field distribution in the HMM waveguide taper for the TM0 mode. (e) The |E|-filed distribution for the |f+> mode (the upper half panel) and |b+> mode (the lower half panel), respectively. (f) The local modal amplitudes of |f+>, |f−>, |b+> and |b−> modes along the z-direction.

Full size image

To provide a quantitative understanding on this mode conversion and light trapping mechanism, the mode expansion method is employed to calculate the amplitude of the local guide modes in the tapered waveguide28. The total field can be expressed as a linear combination of all possible modes supported by the waveguide structure in Eq.(3).

Here the signs “+” and “−” denote the forward- and backward- propagation directions. The expressions of Ex and Hy components for TM0 modes in the HMM waveguide are provided in Section 3 in the supplementary information. ρ represents higher order modes and radiation modes. In a lossy waveguide, we use the unconjugated general form of orthogonality condition26,28, , to obtain the amplitudes of TM0 |f+>, |f−>, |b+> and |b−> modes in the tapered waveguide (i.e. af+, af−, ab+, ab−), as shown in Figure 2f. One can see that the incident TM0 |f+> mode converts to the TM0 |b+> mode near the degeneracy point, while the amplitudes of the other two modes (i.e. |f−> and |b−> modes) are negligible in this structure. Consider that the power flow of the |b+> mode is antiparallel to the propagation direction (the power flow directions for these two eigenmodes are indicated by arrows in Figure 2f), the incident energy therefore escapes from the trapped position through the mode conversion process. To distinguish the mode areas of these two TM0 eigenmodes, the |E|-field for af+|f+> and ab+|b+> are plotted in Figure 2e. When the TM0 |f> mode is launched from the narrow end of the structure, the mode width of the |E|-field distribution is indicated by white dots, showing that the guided modal area shrinks towards the degeneracy point (see the upper half panel). After the mode conversion from the |f> mode to the |b> mode near the degeneracy point, the |b> mode is squeezed into the HMM waveguide taper further due to the smaller modal area (see Figure 2c and the lower half panel in Figure 2e). Due to this decreasing modal area from the |f+> mode to the |b+> mode with a significantly enhanced propagation loss, the tapered HMM waveguide is therefore promising to develop applications for super absorbers29,30 based on the intriguing rainbow trapping effect. In the next section, we consider real and practical metal-dielectric materials to design the HMM waveguide taper and validate the rainbow trapping effect predicted by the effective medium theory.

Numerical validation

As explained previously, the rainbow trapping condition can be fulfilled as long as the HMM can be realized. To validate this prediction, here we investigate a structure consisting of alternating layers of Aluminum (Al) and silicon dioxide (SiO2) films. According to the effective medium theory31, when the film thickness of each layer is much smaller than the wavelength, its permittivity tensor can be approximately described as: , where f is the thickness filling ratio of the metal layer. In this modeling, 16 pairs of Al-SiO2 layer stack are employed to construct the tapered structure along the vertical direction. Considering the dispersive permittivities of real Al and dielectric materials (e.g. SiO2, Si, etc.)32, the HMM condition (i.e. εx < 0, εz > 0) can be automatically fulfilled throughout the visible, near-infrared, mid-infrared and terahertz spectral regions. For instance, in visible to IR spectral region, the effective anisotropic permittivities for a waveguide taper constructed by 15 nm-thick Al and 15 nm-thick SiO2 multi-layers are plotted in Figure 3a, revealing that the HMM condition is met. Therefore, a universal broadband and tunable rainbow trapping effect can be realized based on this practical multi-layered metal-dielectric stack system. To further address the relatively weak coupling from a large plane wave incidence to a single waveguide taper with subwavelength dimensions, we now explore the optical absorption property of a waveguide taper array, as illustrated in Figure 3b. As explained in Section 4 in the supplementary information, the dispersion curve for the HMM waveguide taper array is very close to the one for a single unit HMM waveguide taper. In this modeling, the period of the waveguide taper unit is P = 300 nm and the widths of the top and bottom ends are a = 50 nm and b = 250 nm, respectively. Under an infinitely wide TM-polarized normal plane wave incidence, the absorption spectrum of this HMM waveguide taper array is calculated by FEM simulation, as shown by the black solid curve in Figure 3c. Over 98% light is absorbed in the spectral region from 450 nm to 1.2 μm, which is better than previously reported super absorbers in visible29 and IR domains30. To compare with the effective medium theory prediction, we further model the absorption spectrum of the waveguide taper made by a homogeneous material with effective permittivity tensor elements plotted in Figure 3a, as shown by the red dot curve in Figure 3c, agreeing well with the FEM modeling result shown by the solid curve. Moreover, the |E|-field distribution at different wavelengths of 600 nm, 900 nm and 1200 nm are plotted in the insets of Figure 3c, revealing that different wavelengths are trapped at different positions along the vertical direction of the waveguide taper array. Their trapped positions generally correspond to the degeneracy points predicted in the lossless case and therefore validating the rainbow trapping effect predicted in previous sections. The difference in the short and long wavelength regions are introduced by the discontinuity of the periodic layers at the top and bottom ends of the multi-layered waveguide taper where the effective medium approximation for the TM-polarized light is not applicable33.

Figure 3
figure 3

Light trapping and broadband absorption in a practical HMM waveguide taper array constructed by multi-layered metal-dielectric film stacks.

(a) Calculated spectral dependent anisotropic permittivity of the effective medium constructed by Al and SiO2. The filling ratio of the Al layer is f = 0.5 (e.g. 15 nm-thick Al and 15 nm-thick SiO2 multi-layers). (b) Conceptual illustration of HMM waveguide taper arrays constructed by alternating metal-dielectric films. (c) Modeling of the absorption spectra of an HMM waveguide taper array constructed by 16 pairs of 15 nm-Al/15 nm-SiO2 layers simulated by FEM (the black solid curve) and effective medium theory (the red dotted curve). The period of the waveguide taper unit is P = 300 nm and the widths of the top and bottom ends are a = 50 nm and b = 250 nm, respectively. Inset: The |E|-field distribution in an HMM waveguide taper unit at different incident wavelengths of 600 nm, 900 nm and 1200 nm, respectively.

Full size image

To further demonstrate the slow light nature of the EM modes guided in the HMM waveguide taper, we calculate the dispersion curves of HMM waveguide arrays by solving the eigenequation of the Bloch mode (see Eq.S2 in the supplementary information). The group velocity, vg, of the waveguide mode is given by the slope of the tangent line at a point on the dispersion curve. For w = 109 nm, 163 nm and 226 nm, dispersion curves for lossless structures are plotted by solid lines in Figure 4a–c, respectively. One can see that the vg at the wavelengths of 600 nm, 900 nm and 1200 nm are zero in principle at the degeneracy points indicated by empty circles. However, lossless assumption cannot explain the physics of broadband absorber accurately. When the large absorption of Al is taken into account in the calculation, the dispersion curves split into two branches as shown by the dashed lines in Figure 4. One can see that the vg for both |f> and |b> modes are decreased significantly near the ideal degeneracy point position. Considering the large attenuation coefficient, the Bloch modes become evanescent waves and the power cannot propagate beyond the ideal degeneracy point. As shown in the right panels of Figure 4a–c, the attenuation coefficient of |f> mode is almost zero up to the degeneracy point. As the |f> mode converts to the |b> mode, the mode propagation loss increases significantly, indicating that the enhanced absorption accompanies the intrinsically slow light process in this HMM waveguide taper array constructed by metal and dielectric multilayers.

Figure 4
figure 4

Dispersion curves of Bloch modes in HMM waveguide arrays.

The widths of the core layers are (a) 109 nm, (b) 163 nm and (c) 226 nm, respectively. The red lines represent |f> mode and the blue lines represent |b> mode. The dash lines are the dispersion curves for HMM waveguide array with loss. The frequency dependent attenuation coefficients are shown in the right panel of (a–c).

Full size image

Discussion

In summary, we have explored the feasibility of rainbow trapping based on a multi-layered metal-dielectric film stack supporting broadband slow light resonances. Due to the eigenmode conversion between |f> and |b> modes with significantly different optical properties, the HMM waveguide taper constructed by metal and dielectric films can be used to develop practical on-chip optical super absorbers with a tunable absorption band. Compared with previously reported rainbow trapping platforms6,9,10,11,12,13,14,15, the proposed universal HMM waveguide taper design constitute solid state on-chip photonic architectures capable of simultaneous operation over a wide range of wavelengths throughout visible, near-infrared, mid-infrared27, terahertz (see Section 5 in the supplementary information) and microwave34 spectral regions, which is not limited by severe theoretical constraints required by previously reported INI, IMI and MIM waveguide tapers15. Combined with advanced micro/nanofabrication technologies, this new and robust scheme will make experimental realization of large area on-chip rainbow trapping platforms more achievable, which will pave the way towards on-chip light localization, spectrum splitting15 and super absorbers35 and will impact a broad range of photon-harvesting and energy technologies ranging from photovoltaics36, thin-film thermal absorbers/emitters37, to plasmon-mediated photocatalysis38.