Introduction

The theory of quantum mechanics has proven to be very successful. The theory not only provides precise explanations of many physical phenomena, but also has resulted in the development of many modern technologies1. However, questions regarding the applicability of quantum mechanics to macroscopic systems still exist and the boundary between quantum and classical mechanics remains unclear. The association between classical mechanics and macroscopic systems was tentatively accepted during the early development of quantum mechanics theory2. This viewpoint is embodied in a famous paradox proposed by Schrödinger in 19353, in which he described a “quite absurd” example that a cat state may be alive and dead at the same time. Nowadays, the difficulty of observing the Schrödinger cat state is explained by decoherence, where the superposition of distinct states is destroyed by coupling with unwanted degrees of freedom4.

Leggett-Garg inequalities (LG inequalities) have been derived to clarify the validity of generalizing quantum mechanics to macroscopic systems, based on the macrorealistic theory with macrorealism and noninvasive measurability assumptions5. These inequalities involve a single system with a set of measurements at different times and play a role similar to that of the Bell inequalities in testing local hidden-variable theories6. Introduced as the Bell inequalities in time, the violation of LG inequalities excludes the hidden-variable description based on the above two assumptions.

The two assumptions of the LG inequalities can be extended to any physical system under the classical realistic description if the philosophy of macrorealism is divorced from macroscopic objects. In such descriptions, the state of a system with two or more distinct states will at all times be in one or the other of these states (macrorealism). A corollary of this is that it is possible to determine the state of a system without any disturbance of its subsequent dynamics (noninvasive measurability). The original proposal to realise noninvasive measurement, by coupling the interested system to a probe5, is similar to the Controlled-Not (CNOT) gate where an ancilla is used as the target qubit and the interested system as the control qubit7.

In this study, we experimentally investigate the single photon LG inequalities in a dephasing environment simulated by birefringent media. By implementing an optical CNOT gate on a single photon, the LG inequalities are shown to be maximally violated in a coherent evolution process. This disproves its classical realistic description with the two assumptions of the LG inequalities. With the increase of birefringent media, the violation of LG inequalities becomes weaker and is shown to be not violated anymore at some time. The ability to violate the LG inequalities can be used to set the boundary of the classical realistic description.

Results

Theoretical Schemes

Consider an observable Q(t) of a two-level physical system, where and are the two eigenstates of Q(t) with the eigenvalues of +1 and −1, respectively. The two-times correlation function is defined as . For three different times t1, t2 and t3, (using the same deduction of Huelga et al.8), we can obtain the following:

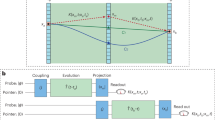
These two inequalities are Wigner type LG inequalities9,10 under the classical realistic description with the two assumptions. To experimentally verify them, the values of K(t1,t2), K(t2,t3) and K(t1,t3) should be measured. If we choose t1 as the initial time, i.e. t1 = 0, we can conveniently use projective measurement at t2 or t3 to get K(t1,t2) or K(t1,t3), because the dynamics after t2 or t3 are not of interest in these two cases. While measuring K(t2,t3), we implemented a CNOT operation that has the ability to realize noninvasive measurement under the classical realistic description at t2 and projective measurement at t3. Figure 1 shows the logic circuit. The two-level ancillary state was initially prepared into the ground state 0 a . The system of interest with initial state ψ (either 0 or 1) evolves in the environment E with an operation of U between t1 and t2 and U' between t2 and t3. At time t2, the physical control system was coupled to the ancilla, which was used as the target system. If the state of ψ is 0, the ancilla remains in 0 a without any change. Otherwise, the state of the ancilla system will be flipped and changed to the excited state 1 a . As a result, by detecting the state of the ancilla, we can know the state of ψ at time t2.

Figure 1
figure 1

Logic circuit to measure the value of K(t2,t3) with a CNOT gate.

0 a is the initial state of the ancilla. ψ is the state of the system (can only be in 0 or 1 during the evolution under the classical realistic description). E represents the environment with the influence U between t1 and t2 and U' between t2 and t3, respectively.

Full size image

Experimental violation of the generalized Leggett-Garg inequalities under decoherence

Photon qubits, which can be easily manipulated at the single qubit level and isolated from the environment, play important roles in quantum communication and quantum computation11,12. The optical CNOT gate has been used to make a strong coupling to an ancilla, for the purpose of measurement of a signal13,14,15,16. By encoding a single photon with several qubits the CNOT gate can be readily realized with simple optical components17. Moreover, by introducing birefringent quartz plates where the coupling between the photon's polarization and frequency modes occurs, we can simulate a fully controllable “environment” to investigate the evolution of the photon state18. Here, we encoded the observable Q(t) as the polarization of a single photon, where the 45° linear polarization state (|H〉 and |V〉 represented the horizontal and vertical polarization states, respectively) is used as |0〉 with the eigenvalue of +1 and the −45° linear polarization state as |1〉 with the eigenvalue of −1. As a result, the observable of Q(t) is the Pauli σx operator. In our experiment, we use a heralded single photon source produced from the pulsed parametric down-conversion process in a nonlinear crystal19. In this process, one photon is used as the trigger, while the other is prepared to be and is used as the initial input state (see Methods for details).

Figure 2 shows the experimental setup for investigating the evolution of the interested photon. Figure 2a shows the setup to measure the value of K(t1,t2). The quartz plate q and a tiltable combination of quartz plates M represent the evolution environment (the total thickness of quartz plates is L). The solid pane M contains two parallel quartz plates (optic axes are set to be horizontal) with the thickness of 8λ 0 (λ 0 = 0.78 μm) and a mutual perpendicular quartz plate with the thickness of 16λ 0, where black bars represent the direction of their optic axes. By tilting these two 8λ 0 quartz plates, we can introduce the required relative phase between H and V. The measurement basis is chosen by a polarizer (P). The photon is then coupled by a multimode fibre to the single photon detector D1 equipped with a Long pass lenses (LP) in front of it, which is used to minimise the background caused by the pump beam light. Figure 2b represents the setup to measure K(t1,t3) with two equal sets of quartz plates of q and M, in which the evolution time is twice of that in Fig. 2a. In our setting, the evolution from t1 to t2 is the same as that from t2 to t3 (the time duration is denoted as t), which means U = U'. In order to measure K(t2,t3), the dashed pane, containing a polarization beam splitter (PBS) and three half wave plates (HWP), with optic axes set at 22.5°, is implemented at time t2 as shown in Fig. 2c. The dashed pane transmits the 45° polarization state (path 1) and reflects the −45° polarization state (path 2). As a result, if the ancilla qubit is encoded as the path information of the photon, the dashed pane acts as the CNOT gate with the path of the photon used as the target qubit and the polarization as the control qubit. Another single photon detector (D2) is applied to detect the photon in the path 2.

Figure 2
figure 2

Experimental setup.

(a) The setup to measure K(t1,t2). The quartz plate (q) with the tiltable combination of quartz plates in the solid pane M represents the evolution environment (black bars represent the optic axes of the quartz). The final measurement basis was chosen by the polarizer (P). The photon was coupled by a multimode fibre to the single photon detector D1 equipped with a long pass lens (LP) in front of it. (b) The setup to measure K(t1,t3). Two equal settings of quartz plates of q and M are used to simulate the environment operators U and U’ in fig. 1. (c) The setup to measure K(t2,t3). The dashed pane containing a polarization beam splitter (PBS) and three half wave plates (HWP) with optic axes set at 22.5° was inserted at time t2. The single photon detector D2 is used to detect the photon in path 2.

Full size image

We first analysed the single photon LG inequalities under the classical realistic description with the two assumptions, where the system can only be in one of the two states H¯ and V¯. If the input photon state is initially in , after evolution time t, the state becomes , where α represents the influence of the environment (i.e., the probability of the photon flips between H¯ and V¯ and it is a function of t with 0 ≤ α ≤ 1). With further identical interaction time t in the same environment, the final state evolves to . Therefore, and , where PGi,Oj (, ) represent the probability of detecting O polarization at time tj when the polarization is G at time ti . For K(t2,t3), with the CNOT operation at t2, we have the probability of 1−α to get H¯ and the final state is the same as ρt after another evolution time t. We also have a probability of α to get V¯ and the subsequent state becomes . As a result, we can get , where PGi represents the probability of detecting G at time ti . It is then easy to verify that and for any α. Therefore, inequalities (1) and (2) are trivial results under the classical realistic description.

Next, we analysed the experiment from the viewpoint of quantum mechanics. For the case of coherent evolution, the evolution effect was imposed by tilting the quartz in M. Because U = U', the induced relative phase between the ordinary and extraordinary light is δ from evolution time t1 to t2 as well as from t2 to t3 and the induced phase from t1 to t3 is 2δ, without the CNOT operation. If the input state is , after passing the first solid pane M the state becomes . As a result, K(t1,t2) = cosδ. With the same analysis, K(t1,t3 ) = cos2δ. When measuring K(t2,t3), if the state is at time t2, its subsequent evolution state is the same as ; if the state is , the subsequent state becomes . Therefore, K(t2,t3 ) = cos2δ which is the same as K(t1,t2). The two generalized LG inequalities can then be calculated as K− = cos2δ−2cosδ and K+ = cos2δ+2cosδ. It can be seen that K− reaches its minimum −1.5 with and K+ reaches its minimum −1.5 with , which both maximally violate inequalities (1) and (2), respectively.

We further considered the decoherent evolution case, which was achieved by increasing the thickness of quartz plate q. In this case, the frequency spectrum of the photon was considered a Gaussian amplitude function, f(ω), with a central frequency, ω 0 corresponding to the central wavelength of 0.78 μm and the frequency spread, σ. For a special frequency ω, after a photon passes through the quartz plates with thickness L the induced relative phase is γω, where γ = LΔn/c. c represents the velocity of the photon in a vacuum and Δn is the difference between the indices of refraction of the ordinary and extraordinary light. With a trace over all the frequency modes, the final forms of the generalized LG inequalities can be written as

Obviously, when thickness L is small, equations (3) and (4) tend toward coherent evolution.

Fig. 3a shows the corresponding values for individual correlations K(t1,t2), K(t2,t3) and K(t1,t3), which are used to get the values of K− in the inset of Fig. 3b. The solid line, dashed line and dotted line correspond to theoretical predictions (the solid line and the dashed line completely overlap and only the solid line can be seen). We find that K(t1,t2) = K(t2,t3) and the oscillation period of K(t1,t3) is twice as that of K(t1,t2) (K(t2,t3)). These findings are consistent with theoretical predictions. Fig. 3b shows the envelope evolution of K−. When the thickness of quartz plates is small, the generalized LG inequality is violated according to the previous analysis. From the inset in Fig. 3b, which represents the oscillation between the maximum and minimum in the blue dashed pane, we find that the minimum of K− reaches −1.544±0.056, which violates the classical limit of −1 by about 9.7 standard deviations. With the increase in thickness of quartz plates (L), the violation of the LG inequalities becomes gradually weaker. K− does not violate the classical limit −1 when L is increased to about 33λ 0. This implies that when L is larger than 33λ 0, the evolution trajectory can be described by the classical realistic description and when L is smaller than 33λ 0, the trajectory must adopt the quantum description. Therefore, we have set a boundary for the classical realistic description by using the LG inequalities. Errors are mainly due to the random fluctuation of each measured coincidence count and the tilt uncertainties of quartz plates (we tilt quartz plates to introduce the required relative phase between horizontal and vertical polarizations). Solid lines are the theoretical predictions of K−, employing equation (3) with σ fitting to 3.56×1013 Hz.

Figure 3
figure 3

Violating the LG inequality with K−.

(a) The corresponding values for individual correlations K(t1,t2), K(t2,t3) and K(t1,t3) to get K− in the inset of (b). The solid line, dashed line and dotted line are the corresponding theoretical predictions (the solid line and the dashed line completely overlap and only the solid line can be seen). The x axis represents the total thickness of quartz plates between t1 and t2. (b) The envelope evolution of K−. Red dots represent the experimental results. Solid lines are the theoretical fittings employing equation (3). The dashed line represents the classical limit, −1. The x axis represents the total thickness of quartz plates between t1 and t2. The inset displays the oscillation between the maximum and minimum in the blue dashed pane (the x axis represents the total thickness of quartz plates between t1 and t2 and the y axis represents K−). Error bars correspond to the random fluctuations of each measured coincidence count and the tilt uncertainties of quartz plates. λ 0 = 0.78 μm.

Full size image

We further show the envelope evolution of K+ in Fig. 4. At the beginning of the evolution, the minimal value of K+ reaches −1.495±0.052, which violates the classical limit of −1 by about 10 standard deviations. When L increases to about 33λ 0, it does not violate the classical limit anymore. The inset shows the oscillation between the maximum and minimum in the blue dashed pane, which displays the critical boundary. Solid lines are the theoretical predictions employing equation (4).

Figure 4
figure 4

Violating the LG inequality with K+.

Red dots represent the experimental results. Solid lines are the theoretical fittings employing equation (4). The dashed line represents the classical limit, −1. The x axis represents the total thickness of quartz plates between t1 and t2. The inset represents the oscillation between the maximum and minimum in the blue dashed pane (the x axis represents the total thickness of quartz plates between t1 and t2 and the y axis represents K+). Error bars correspond to the random fluctuation of each measured coincidence count and the tilt uncertainties of quartz plates.

Full size image

Discussion

In our experiment, the polarization of a photon was used as the observable Q(t). This measured quantity could also be considered as the evolution path of the photon. A photon with different polarizations passes through different paths, separated by the polarization beam splitter. This phenomenon is similar to that of the position of a single electron in a double quantum dot20. The violation of generalized LG inequalities implies that at least one of the two assumptions in the classical realistic description is untenable and disproves the definite classical evolution trajectory20. In our experiment, the information carrier (polarization) and the environment freedom (frequency) are encoded on the same photon. The experimental results can be repeated by a corresponding diagonally polarized input laser pulse, in which each of the photons in the laser pulse undergoes the same evolution. The polarization of a “classical” light (laser pulse) can also be viewed as a consequence of the transverse vector of electromagnetic field that is allowed to be superposed, in which Q(t) ranges continuously from −1 to 1. This condition is different from the initial assumption that Q(t) can only be of 1 or −1 at each measurement in our case. As a result, the violation of LG inequalities with “classical” light does not contradict that case of single photon.

Recently, the violation of generalized LG inequalities has been demonstrated by employing weak measurements on a single photon21 and a superconducting quantum circuit22. The generalized LG inequalities used in these studies are similar to the Wigner version used here, which are derived from the classical realistic description with the two assumptions. The weak measurement provides the ability to control the back action on the system in the sense of quantum mechanics. In our experiment, we directly test the LG inequalities by using a CNOT gate which implements non-invasive measurement under the classical realistic description. This kind of classical non-invasive measurement is also implemented by Knee et. al.23. Our method is directly related to the problem of decoherence. By changing the thickness of quartz plates, we can control the evolution time of a single photon between sets of measurements. The ability to violate generalized LG inequality sets the boundary of the classical realistic description.

In our experiment, the coherence length of the initial photon state (l0) is about 53 μm (calculated by 2πc/σ). As a result, at the crossover point where the LG inequalities are not violated, the thickness of quartz plate of 33λ 0 corresponds to about 0.486 l0 (calculated by (33λ 0/53)l0 and λ 0 = 0.78 μm). The theoretical form of the output photon state at t2 becomes with a visibility of 0.56 (the corresponding experimental value is 0.558±0.004). The visibility is calculated by , where pi represents the corresponding detecting probability (). The visibility characterizes the purity of the final state for the measure base is . When the visibility of the photon state at t2 is reduced to less than 0.56, the LG inequalities would not be violated anymore. The state at the transition point where the LG inequalities are not violated still has coherence between the two orthogonal states. It is similar to the case that not all entangled states violate a Bell inequality24. Therefore, the ability to violate LG inequalities, which sets the boundary of the classical realistic description, may connect to the ability to perform some quantum information task with quantum advantages as that of Bell inequalities.

In summary, we experimentally violated two generalized LG inequalities in an all-optical system using a CNOT gate. The violation of generalized LG inequalities disproves the definite classical evolution trajectory of the single qubit20 and implies that at least one of the two assumptions in the classical realistic description is untenable. The ability to violate LG inequalities can be used to set the boundary of the classical realistic description.

Methods

In our experiment, the photon of interest was prepared from a heralded single photon source, which was produced from a pulsed parametric down-conversion process. A mode-locked Ti:sapphire laser with a centre wavelength mode locked to 0.78 μm (130 fs pulse width and 76 MHz repetition rate) was used to pump a 2 mm type-I β-barium borate (BBO) crystal which generated the second harmonic ultraviolet pulses (0.39 μm). These ultraviolet pulses were then focused into a 2 mm type-II BBO crystal which was cut for beamlike phase matching25,26 to produced bright down-conversion photon pairs. The evolution of one of the photons was investigated by preparation into and passing it through the experimental setup in Fig. 2. The other photon was used as the trigger. We obtained about 18000 coincidence events per second and the integration time was 10 s for each measurement.