Introduction

If clonal affiliation cannot be determined directly by proving the common descent of a collection of individuals via vegetative propagation (including observations of physiological connectedness), one mostly depends on analyses of genetic identity. Since genetic identity for a limited number of genetic traits is by itself not a reliable indicator of joint clonal origin, common approaches try to reject the hypothesis that an observed collection of individuals which are identical for a specified number of genetic traits results from sexual (generative) propagation. This is usually done by specifying the characteristics ideally associated with sexual reproduction, namely stochastic independence between gene loci and random mating. This provides a hypothesis based on the population frequency p of the target genotype, which is obtained by forming the product of the pertinent single-locus gene frequencies observed in the sample.

The number of individuals in a sample that show the target genotype is then assumed to be distributed binomially based on the hypothetical target genotype frequency p. The hypothesis that the n individuals showing the target genotype in a sample of size N result from sexual propagation is rejected in favor of clonal propagation if the probability

is small (see eg Frascaria et al, 1993; Parks and Werth, 1993). CnN is the probability of obtaining n or more copies of a genotype in a sample of size N, given the genotype has frequency p in the base population. The intuitively appealing rationale behind this approach is that sexual propagation should be very unlikely to be responsible for the observed n or more copies. This approach seems to prevail in all investigations applying genetic markers for clone identification (for a more recent application see eg Ivey and Richards, 2001).

There are two basic weaknesses in this approach. One concerns the tacit assumption that sexual reproduction can be sufficiently characterized by independent association among genes in genotypes (both at single loci and between loci). This assumption is unlikely to apply to a broad spectrum of organisms such as partially self-fertilizing plants, as is well known (see eg Bennet and Binet, 1956; Ziehe and Roberds, 1989). The other weakness concerns understanding of the probability CnN as a statistical means of testing the hypothesis of sexual against asexual reproduction (see eg Stenberg et al, 2003).

Therefore, in the present paper the conceptual underpinnings of the approach are discussed, its limitations outlined, and its statistical treatment explained. Special emphasis is put on a critical evaluation of ways to characterize sexual reproduction in terms of forms of association among genes in genotypes. Since problems of estimating numbers of clones or clonal diversity in populations cannot be meaningfully treated unless reliable methods of detecting asexual propagation of individual genotypes are available, the following considerations focus on the development of such methods.

Conceptual considerations

To prevent misunderstanding due to differential use of terminology, recall that vegetative or asexual reproduction involves mitoses only, and that a clone is defined as a set of individuals all of which derive from a common ancestor by mitoses. Therefore, disregarding mutation or mitotic irregularities, all members of a clone are genetically completely identical. An asexual origin of an individual implies that there exists at least one other individual to which it is completely identical genetically. This other individual is either the clonal parent (ortet), a clonal sibling, or a clonal offspring of the first individual. A clone comprises clonal parents, siblings, or offspring, and it consists of at least two individuals (ramets). Hence, from an independent observation of a single individual, nothing can be concluded as to its vegetative (asexual) or generative (sexual) origin. If at least one member of a group of individuals differs in at least one genetic trait from the other members, the group either consists of different clones or contains at least one sexually produced member.

Since differences in genotype can be due either to mutation or to recombination events (in the general sense, including mating) during sexual reproduction, clonal differences must be traceable to these events. If mutation does not play an important role, different clones must be considered to have originally arisen through sexual reproduction. When emphasizing the fact that a clone is traceable to a sexually produced ancestor, the term “genet” is used to describe the totality of individuals derived by asexual reproduction from this ancestor. In this context, a genet is sometimes considered as a single individual, particularly if the parts are physiologically connected.

There are thus basically two ways to characterize a clone. The one refers to a collection of individuals, all of which are identical for all of their genetic traits. The other refers to the fact that all members of the collection are reproduced asexually from a common ancestor. The first characterization emphasizes the genetic state (genetic identity) and the second emphasizes the mode of propagation (ie vegetative or asexual propagation). Accordingly, methods of clonal identification can be based on the genetic state or on the mode of propagation, where vegetative or asexual propagation processes are understood to regularly produce individuals of identical genetic state. Since in many cases direct proof that two individuals are related by asexual propagation is difficult to obtain, methods relying on analyses of genetic states have priority.

An assessment of genetic state is of course feasible only for a quite limited number of genetic traits. Any conjecture of affiliation of the members of a group to one clone is therefore based on the observation of their identity for a specified set of genetic traits. The question thus is how identity for all genetic traits in a group of individuals can be predicted from the observation of identity for a comparatively small sample of genetic traits. Since the hypothesis of identity for all genetic traits is falsified only if at least one member of the group differs for at least one trait from the others, it appears that there is no answer to this question. If, on the other hand, modes of propagation are considered for the explanation of the observed genetic identity, the focus is set on methods to falsify the hypothesis of asexual or of sexual propagation. As in the case of complete genetic identity, asexual propagation cannot be falsified on the basis of observations of identity for a limited number of genetic traits.

This leaves us looking for methods to falsify sexual propagation as the mode of propagation that brings about genetic identity among individuals. Such falsification would again not be possible if it could be demonstrated that for each genotype there exists a system of sexual reproduction that produces the genotype at arbitrary frequencies. There indeed always exists such a system, as can be seen when viewing any target genotype as the combination of two gametes. Each of these gametes could be produced by individuals that are completely homozygous for the genes located at the gamete. A population that consists of only these two genotypes could produce offspring showing the target genotype at arbitrary frequencies, depending on the mating preferences between the two homozygotes. Such situations are conceivable in autogamous plants with occasional cross-fertilization. Consequently, the hypothesis of sexual production of a genotype cannot be falsified unless definite constraints can be specified to which a particular system of sexual reproduction is subjected. If these constraints axe violated by an observation, sexual propagation is rejected in favor of asexual propagation.

Specification of characteristic constraints for sexual reproduction

Sexual reproduction operates on genes as the units of information that are identically transmitted over generations. The mechanisms of sexual reproduction realize associations among genes according to their basic specifications. Thus, if panmixia is such a specification that applies to a given number of incompletely linked gene loci over a sufficient number of generations in a large population, the genotype frequencies at these loci would result from the product of the corresponding gene frequencies. As was mentioned above, this seems to be the prevailing characterization of sexual reproduction used in clonal analyses. Deviations from this basic model include gene associations that may be generated by non-random mating and may appear as deviations from Hardy–Weinberg proportions at individual loci or as stochastic associations between loci. Indices that characterize such homologous and nonhomologous gene associations under the restrictions set by the underlying gene frequencies could then help to outline typical constraints set by the respective mechanisms of sexual reproduction. To distinguish these indices from those that do not consider the restrictions by gene frequencies, they will be referred to as relative associations in the following.

Characteristics of genetic structures that result from sexual reproduction can ideally be studied at the zygotic stage. Genetic structures at later stages can be modified by viability selection or asexual propagation. Hence, in order to avoid circular reasoning in the usage of relative gene associations for testing clonal propagation, as a reference these associations ought to be determined at stages close to the zygotic stage. This is different for the frequencies of the genes, since these contain no information that specifically refers to sexual reproduction. Therefore, two basic prerequisites for clonal analyses are (i) knowledge of relative gene associations that typically show at the zygotic stage as the result of a species’ or population's mechanisms of sexual reproduction and (ii) observations on genetic structures at later stages.

Once relative gene associations are found that are characteristic of zygotic stages, these associations can be used together with gene frequencies observed in later vegetative stages to derive more realistic hypotheses on genotype frequencies that retain the characteristics of sexual reproduction. These frequencies would then form the basis for tests aiming at the rejection of sexual reproduction in favor of asexual propagation.

Clonal propagation is expected to increase the frequency of some multi-locus genotypes in relation to sexual propagation. In terms of relative frequencies, this implies that there ought to be other genotypes which decrease in frequency and may therefore be present at lower frequency than expected if sexual propagation had realized all of the combinations of genes present in the population. For large amounts of clonal propagation of some genotypes, this could even lead to complete absence of other genotypes that could have been produced sexually from the genes present in the cloned genotypes. At the other extreme, it is conceivable that all genotypes are present in proportions that are typical of sexual reproduction, but each genotype is cloned by the same amount. In this case, sexual reproduction cannot be distinguished from asexual reproduction on the basis of genotypic frequency distributions.

Genetically differential asexual reproduction therefore is a prerequisite for detecting clonal propagation. The fact that genotype frequencies in excess of sexual reproduction must be compensated by genotype frequencies below the expectation of sexual reproduction can be used for a test of the presence of asexual propagation in a population. The test simply consists in finding genotypes that are less frequent than expected from sexual reproduction and checking for statistical significance of this observation. On the other hand, identification of individual clones requires testing for excess in frequency of a particular genotype over the frequency expected from sexual reproduction.

Relative measures of gene association

As was argued above, associations among genes in genotypes that result from sexual reproduction should be characterized within the limits set by the gene frequencies. Such relative measures of association must therefore consider genotype frequencies within the greatest lower (α(g)) and least upper (ω(g)) bounds set by the population frequencies of those genes that are represented in the genotype g. It is shown in the Appendix that

where the subscripts i;l and j;l indicate the two alleles present in genotype g at the lth gene locus (i=j indicates homozygosity) among L gene loci, pi;l denotes the population frequency of allele i at the lth locus, and δij;l=0 for i≠j (heterozygous locus) and=1 otherwise (homozygous locus). The frequency P(g) of genotype g thus lies in the interval α(g)≤P(g)≤ω(g).

Any measurement of degrees of association must be based on a concept of the absence of association. This concept is generally agreed to be specified by stochastic independence in association of the involved units. In the present case, where genes are considered as units, the absence of association of the genes of a genotype g is defined by

The simplest measure of association is one that places the situation of stochastic independence in the center of an interval, the extremes of which reflect the lower and upper bounds set by the reference gene frequencies, and that varies linearly within the extremes. Such a measure, with extremes −1 and +1, is provided by

Positive and negative values of Ar(g) indicate genotype frequencies that exceed and fall short of, respectively, the situation of the absence of association as specified by P̃(g) The relation of this measure to the common measure of standardized gametic disequilibrium is demonstrated in the Appendix.

It is easily verified that the lower bound α(g) equals 0 if the genotype g is heterozygous for at least one locus. Even if g were homozygous at all loci, α(g)=0 if for at least one locus the frequency of the pertaining allele were less than or equal to ½. Hence, in the vast majority of cases it is very likely that α(g)=0.

Characterization of sexual reproduction by gene associations

Suppose that an estimate Âr(g) of Ar(g) has been obtained for a genotype g at the zygotic stage, such that this estimate can be considered to reflect typical effects of sexual reproduction. Applying the estimate to gene frequencies observed in a later target stage that possibly involves asexual reproduction, a hypothesis can be generated on the frequency H(g) of the genotype g that would result from these gene frequencies if the genotype were produced sexually. The hypothesis can be obtained from setting Âr(g)=Ar(g) and H(g)=P(g) in equation (4) and solving this for H(g):

Recall that the allele frequencies entering ω(g), α(g) and P̃(g) are those observed at the target stage. In this context, Âr(g)=0 represents the common hypothesis H(g)=P̃(g) on sexual reproduction.

Problems in obtaining the estimate Âr(g) of Ar(g) at the zygotic stage may be due to the fact that the genotype g did not appear in the sample taken at that stage. In this case, the sample size sets limits to the maximum frequency with which the genotype may escape notice even though it is present among zygotes (see Gregorius, 1980). An estimate of Ar(g) can then be based on this maximum frequency.

Another problem may be due to the lack of genetic markers that can be observed at both the zygotic and the target stages. A remedy could then be provided from observations of Ar which show sufficient degrees of regularity with respect to more general genetic characteristics. An example could be degrees of heterozygosity, for which Ar varies only moderately with number of loci. If such regularity in associations is not observable, a last means consists in determining typical ranges of variation of Ar and utilizing these ranges in setting limits to H(g).

Statistical basis of testing asexual propagation

It was argued above that candidates for clonal propagation are genotypes that are observed at higher frequency in a sample than can be expected from sexual reproduction. Given a hypothesis on the frequency H(g) of a genotype g resulting from sexual reproduction, this hypothesis would thus be rejected in favor of clonal propagation if a number n of copies of g is obtained in a sample of size N such that n/N ‘significantly’ exceeds H(g). The above-introduced cumulative binomial probability CnN is commonly used as the pertaining significance probability, where p=H(g).

To understand the system analytical basis of this significance probability, recall that the absence of clonal propagation of a genotype g comprises not only the situation where the frequency P(g) of that genotype is equal to the frequency H(g) expected for sexual reproduction but additionally comprises all situations where P(g)<H(g). This was shown to follow from the fact that clonal propagation of one particular genotype must be compensated by a frequency reduction of other, sexually produced genotypes. Hence, any model of the absence of clonal propagation of a particular genotype g is characterized by a parameter q=P(g) which lies in the closed interval with p=H(g). Consequently, rejection of the absence of clonal propagation requires rejection of all parameters from 𝐻.

Since only observations that lie outside of 𝐻 may lead to rejection of 𝐻, a discrepancy measure between observations and parameter values is required that makes no distinction between values from 𝐻. Proceeding from a primary discrepancy measure d between observations (n/N) and model parameters from 𝐻, this can be achieved by defining a new discrepancy measure d̂ by for any q ∈ 𝐻 (note that n/N ∈ 𝐻 implies d̂(n/N, q)=0).

For q ∈ 𝐻, the significance probability P(n; q) of an observation n is given by , where . Since the model is to be rejected or accepted as a whole and thus for all parameters from 𝐻, the significance probability P(n; q) must be determined for the worst possible case. This yields a significance probability P(n; 𝐻 specified by . Choosing d(i/N, q)=∣i/N–q∣ as initial discrepancy measure, one obtains d̂(i/N, q)=i/N−p for i/N ∈ 𝐻 and thus i/N>p. From the fact that CnN decreases with decreasing p as long as p≤n/N, one indeed obtains P(n; 𝐻) = CnN for n/N>p and P(n; 𝐻) = 1 for n/N≤p.

The system analytic approach thus confirms the appropriateness of the one-sided testing procedure implicit in CnN. This seems to contradict the statement of Stenberg et al (2003) that CnN ‘should be viewed as a test statistic’ rather than ‘as a true probability’ from which it can be ‘concluded that values below 0.05 are significant at the 5% level’. From the context of this statement, however, it becomes clear that the authors did not intend to apply CnN to the situation of testing clonal propagation of individual genotypes. Moreover, it should be kept in mind that rejection of the hypothesis of sexual reproduction of a genotype g for small values of CnN in essence is based on rejecting a genotype frequency that is smaller than or equal to some hypothetical threshold frequency H(g). Whether this implies that all or only some of the n individuals are asexually propagated will be discussed in the following section.

Number of clones among genetically identical individuals

If sexual propagation of a genotype g is rejected, this does not imply that all representatives of g belong to one clone. There is still the possibility that different clones exist in the genetic background of g. This raises the question of how many clones can be maximally expected among the n representatives of g observed in a sample of size N. To answer this question, recall that the hypothesis that all of the n representatives of a genotype observed in a sample of size N are produced sexually is rejected if CnN<ɛ for some significance level ɛ. This is tantamount to rejecting the hypothesis that more than n−1 clones exist among the n representatives of g.

Since CkN is a decreasing function of k, there exists a unique number m=m(ɛ, N), which is obtained as the smallest number k for which CkN<ɛ, that is,

Clearly, m≤n, and m−1 is the maximum number of clones which can be assumed to be represented among the n representatives of genotype g. The case m=2 is of particular interest, since it concerns rejection of the hypothesis that the representatives of the genotype consist of more than one clone. In this case, C2N=1−(1−p)N−1(1+(N−1)p)<ɛ, where p=H(g). Hence, if at least two individuals show the same genotype g and C2N<ɛ, all representatives of this genotype can with high probability be expected to belong to a single clone. The same of course holds true if m=1 or 0.

It follows that, once the hypothetical frequency H(g) of a (multi-locus) genotype g, the sample size N and the significance level ɛ are specified, the maximum number of clones of the genotype g that the sample is likely to contain is determined by m(ɛ, N)−1. More precisely, given these specifications, the hypothesis that the genotype consists of more than m(ɛ, N)−1 clones is rejected with probability 1−ɛ if at least m(ɛ, N) copies of the genotype are observed in the sample. If at least one copy of the genotype is observed, the cases m(ɛ, N)=0 and m(ɛ, N)=1 have the same interpretation as m(ɛ, N)=2.

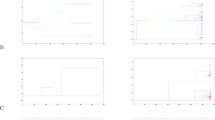
The probably most important result of these considerations is that rejection of the hypothesis of sexual reproduction in favor of membership of all copies of a genotype to a single clone is based on C2N, irrespective of the actual number n≥2 of observed copies. It is thus not sufficient to base the decision on clonal propagation on the probability of randomly drawing exactly two identical genotypes (see Chung et al, 2000). Even if only one copy of the genotype is observed, this can be attributed to the result of clonal propagation if C1N=1−(1−p)N is below the level of significance. A characterization of C2N is provided by Figure 1. It is seen that C2N increases for each given hypothesis H(g)=p with the sample size N. The probability of detecting clonal propagation thus decreases with increasing sample size. This apparently counterintuitive observation follows from the above demonstrations, which imply that increasing the sample size increases the chances to include more of the clones hidden in the background of the observed genotype g.

Figure 1
figure 1

Significance probability C2N as a function of the frequency p of a specified multilocus genotype expected under sexual reproduction. The functional relationship is demonstrated for several sample sizes N. The two dotted horizontal lines mark the two most frequently applied significance levels 0.05 and 0.01.

Full size image

Concluding remarks

The detection of clonal propagation with the help of specified gene markers involves two steps. In the first step, genotype frequencies are characterized that are typical of sexual reproduction. The second step concerns tests for accordance of the observed genotype frequencies with those typically expected under sexual reproduction. Rejection of the hypothesis in favor of membership to a single clone requires a significant C2N probability.

If, for an observed number n>2 of genetically identical individuals, CnN is significant but C2N is not, further information may be available to decide upon the possibility that all individuals nevertheless belong to a single clone. Such information may be provided by the spatial distribution of genetically identical individuals, for example, if clonal propagation is known to take place by root suckers.

When, within the same sample, more than one multilocus genotype is suspected to result from clonal propagation, the principle of the testing procedure remains the same as for a single genotype. The significance probability then equals the probability of having each of the genotypes in question be represented by at least two individuals in the sample, given all of these genotypes are produced sexually. Estimates of numbers of clones can be based on such a test.

The more crucial step, however, is the first one, which is concerned with the characterization of genotype frequencies resulting from sexual reproduction. It was emphasized above that this characterization relies on associations between genes but not on the frequency distributions of genes. Any pattern of gene frequencies can be equally generated by sexual or asexual reproduction. The difference between the two modes of reproduction shows up solely in the relative associations among genes. This is why gene frequencies can be determined at any developmental stage, while relative gene associations should be preferentially determined at developmental stages, such as seed, in which the effects of sexual reproduction are not likely to have been altered by clonal propagation.

Experimental estimates of relative gene associations seem to be based solely on the ‘standardized gametic disequilibrium’. This index was suggested by Lewontin (1964), and its properties are further detailed in Hedrick (1987) and Lewontin (1988), for example. Applicability of the index is restricted to pairwise considerations of loci in haplotypes and two alleles per locus, and it is usually estimated from frequencies of diploid genotypes under strong model assumptions. As is shown in the Appendix, this index is a special case of the present measure Ar, when applied to haplotypes at two loci (see Appendix). Thus, probably little is known about relative gene associations at multiple loci in real populations.

In order to demonstrate effects of sexual reproduction on relative gene associations, one therefore depends on model populations such as those described by the mixed mating model, in which partial selfing is known to produce associations among loci. An algorithm is given by Ziehe (2003, p 87f), that allows computation of equilibrium frequencies of the degrees of heterozygosity for two equally frequent alleles at arbitrary numbers of diploid loci. For each degree k of heterozygosity, there are different genotypes that are heterozygous for k among n loci and that are equally frequent as a consequence of equal allele frequencies. This allows computation of Ar(g) values for individual genotypes g. Numerical exploration indicated that Ar(g) always stays above −σ (where σ is the proportion of selfed individuals) and reaches positive values only for low degrees of heterozygosity. With increasing number n of loci, the positive values of Ar(g) quickly approach zero (for example, for five gene loci and σ=0.3, the largest value of Ar is 0.006, and it is reached for homozygosity at all loci).

This suggests a tendency for self-fertilization to produce predominantly negative relative gene associations, so that H(g)≤P̃(g) by equation (5). Thus, for mating systems involving random mating or partial self-fertilization, the common tests of clonal propagation are conservative (provided CnN and C2N are used appropriately), since P̃(g) (as specified in equation (3)) constitutes the hypothesis of sexual reproduction in these tests. Yet, the suggestion of predominantly negative relative gene associations in partially selfing or autogamous populations awaits experimental verification. The effects of negative assortative mating (as in self-incompatibility systems) on relative gene associations at multiple loci are altogether unknown both theoretically and experimentally. The measure Ar may help to direct studies towards this end.

Thus, the essential steps of the proposed method of testing for clonal propagation can be summarized as follows: Given a genotype that is specified for a number of marker gene loci and for which at least two copies are observed in a sample from the target population, then (i) obtain an independent estimate of the relative gene association Ar for the genotype (as described in equation (4)) that is characteristic of the mating system of the target population or species (this may be based on simulations of realistic models or on empirical studies of mating systems), (ii) estimate from the sample the genotype frequency and the frequencies of those genes appearing in the genotype, (iii) determine from these frequency estimates the lower and upper bounds α and ω for the genotype according to equation (2) and compute the reference frequency P̃ for the genotype according to equation (3), (iv) insert these quantities into equation (5) to obtain the frequency H(g) of the genotype expected under the hypothesis of sexual reproduction, (v) compute the probability C2N for this expected frequency, and (vi) accept the hypothesis that all copies of the genotype observed in the sample belong to a single clone if C2N is below the chosen significance level.