Three-dimensional non-Abelian quantum holonomy

Abstract

When a quantum system undergoes slow changes, the evolution of its state depends only on the corresponding trajectory in Hilbert space. This phenomenon, known as quantum holonomy, brings to light the geometric aspects of quantum theory. Depending on the number of degrees of freedom involved, these purely geometric entities can be scalar or belong to a matrix-valued symmetry group. In their various forms, holonomies are vital elements in the description of the fundamental forces in particle physics as well as theories beyond the standard model such as loop quantum gravity or topological quantum field theory. Yet, implementing matrix-valued holonomies thus far has proven challenging, being further complicated by the difficulties involved in identifying suitable dark states for their construction in bosonic systems. Here we develop a representation of holonomic theory founded on the Heisenberg picture and leverage these insights for the experimental realization of a three-dimensional quantum holonomy. Its non-Abelian geometric phase is implemented via the judicious manipulation of bosonic modes constructed from indistinguishable photons and obeys the U(3) symmetry relevant to the strong interaction. Our findings could enable the experimental study of higher-dimensional non-Abelian gauge symmetries and the exploration of exotic physics on a photonic chip.

Main

Gauge symmetries play a crucial role in any field theory, both classical and quantum¹. Perhaps the best-known incarnation of this concept is the vector potential that governs the interaction of electrons with the electromagnetic field² that, being represented by an Abelian gauge field, is associated with the U(1) gauge symmetry of the electron wave function. In general, gauge fields can be non-commuting or matrix valued (that is, non-Abelian) and, thus, correspond to unitary groups of higher dimensions. For example, despite their different origins in three distinct fundamental forces, the spin of electromagnetism, the weak isospin of the weak interaction and the isospin of the strong interaction all transform under the two-dimensional special unitary group^3,4 SU(2). Notably, the full description of the strong interaction in quantum chromodynamics is based on the special unitary group SU(3), where the three colour charges⁵ play a role similar to the one-dimensional electrical charge in electromagnetism^1,6. Another aspect of gauge fields is the emergence of geometric phases—topological structures that depend solely on the geometry of the underlying space and the specific trajectory of a system through it. While gauge fields, by their very nature, are not observable quantities, geometric phases can indeed be measured and therefore act as indicators of the underlying symmetry group. A famous example of a geometric phase is the Abelian Berry phase⁷ associated with the group U(1). As the dimension of the gauge field increases, the dimension of the corresponding geometric phase, or holonomy, increases accordingly⁸. In contrast to dynamical phases, which constitute the internal clock of a quantum state, geometric phases cannot be made to disappear by gauge transformations. They are a characteristic feature of the system⁷.

Holonomies are a common feature in non-perturbative approaches to quantum chromodynamics, such as lattice gauge theory^9,10. Additionally, they are prominent in topological quantum field theory^11,12, as well as loop quantum gravity¹³, where they serve as the fundamental objects from which correlation functions are obtained. Consequently, the realization of gauge fields^14,15 and holonomies is relevant to the quantum simulation of fundamental physics, lattice gauge theory^16,17 and topology^18,19,20. A particularly promising application of holonomies is so-called holonomic quantum computing^21,22. This recently proposed paradigm has been shown to be universal²³ and, given that holonomies only depend on the area enclosed by their path through parameter space, holds the promise for a new class of robust quantum architectures composed of gates whose functionality is inherently protected by topology²⁴. So far, holonomies have been implemented in neutral atoms²⁵, superconductors²⁶, optical fibres²⁷ and integrated photonic waveguides²⁸. Yet, despite the diversity of these platforms, only two-dimensional holonomies have been realized thus far, effectively limiting potential holonomic quantum simulations to only the (weak) isospin without the possibility to account for colour charges. Here, we present an experimental realization of a three-dimensional holonomy. To this end, we exploit a degree of freedom that is unique to bosonic systems by using two indistinguishable photons, corresponding to a simultaneous excitation of two bosonic modes. The ability to carry out holonomic operations in the context of U(3) constitutes an important first step towards the experimental study of analogies of quantum chromodynamics as well as aspects of non-Abelian lattice gauge theories.

Synthesizing the non-Abelian geometric phases associated with quantum holonomies demands a highly symmetric system, as its Hamiltonian ${\hat{H}(t)}$ has to support a degenerate eigenspace ${{{\mathcal{H}}}}_{{{\mathrm{D}}}}$ spanned by a set of zero-energy eigenstates $\left| {D_k(t)} \right\rangle$, $k = 1, \ldots ,N$ that henceforth will be referred to as ‘dark’ space/states. Expressed in terms of accessible physical parameters $\left( {\kappa _\mu (t)} \right)_{\mu = 1:\delta }$, the explicit time dependence of the system corresponds to a path $\gamma (t)$ in the δ-dimensional parameter space ${{{\mathcal{M}}}}$. As illustrated schematically in Fig. 1, an initially prepared state $\left| {\varPsi (t_{{{\mathrm{i}}}})} \right\rangle$ is transformed into a final state $\left| {\varPsi (t_{{{\mathrm{f}}}})} \right\rangle = \hat U\left( \gamma \right)\left| {\varPsi (t_{{{\mathrm{i}}}})} \right\rangle$, where the unitary ${\hat U}\left( \gamma \right)$ is the desired holonomy. It follows that the path has to be closed $\left( {\gamma \left( {t_{{{\mathrm{i}}}}} \right) = \gamma (t_{{{\mathrm{f}}}})} \right)$ as well as adiabatic²⁹, that is, sufficiently slow to ensure that the state remains strictly in the dark space at all times $t_{{{\mathrm{i}}}} < t < t_{{{\mathrm{f}}}}$. Notably, the N-fold degeneracy of ${{{\mathcal{H}}}}_{{{\mathrm{D}}}}$ generalizes Berry’s original construction⁷ to the case where the associated symmetry group is the N-dimensional unitary group⁸ U(N). The parallel transport of $\left| {\varPsi (t)} \right\rangle$ along $\gamma (t)$ is mediated by a gauge field $\hat A_\mu$, also known as the adiabatic connection, and any change of gauge in ${{{\mathcal{H}}}}_{{{\mathrm{D}}}}$ accordingly leaves all measurable consequences of the theory unchanged. In particular, the trace of the unitary $\hat U\left( \gamma \right)$, the Wilson loop⁹ ${{{\mathcal{W}}}}_\gamma = {{{\mathrm{Tr}}}}\left[ {\hat U\left( \gamma \right)} \right]$, can therefore serve as a gauge-invariant characteristic of the holonomy.

Fig. 1: Schematic illustration of a holonomy.

In a curved parameter space ${{{\mathcal{M}}}}$ (that is, with non-trivial topology) spanned by the coefficients $\kappa _{{{{\mathrm{W}}}}/{{{\mathrm{E}}}}/{{{\mathrm{A}}}}}$ (magenta surface), a system propagates along a closed loop γ such that the initial and final coupling configurations coincide at a point κ₀. Meanwhile, the evolution of quantum states occurs in Hilbert space, within which the dark states of the system span a distinct dark subspace ${{{\mathcal{H}}}}_{{{\mathrm{D}}}}$. While the configurations of these dark states at the beginning and end of the propagation are identical, an initial quantum state $|\varPsi{_i}\rangle$ accumulates a geometric phase that depends solely on the area enclosed by γ, the signature of a quantum holonomy.

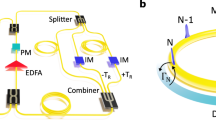
To harness this concept, we employ a star graph of bosonic modes (Fig. 2a), where each of three outer modes (identified as ‘west wing’ W, ‘east wing’ E and ‘auxiliary’ A) couples solely to the central mode C along the propagation direction z via the parameters $\kappa _\mu (z)$, $\mu \in \left\{ {{{{\mathrm{W}}}},{{{\mathrm{E}}}},{{{\mathrm{A}}}}} \right\}$ (Fig. 2b). With a coupled mode ansatz, the system’s Hamiltonian is given by $\hat H = \Sigma _\mu \kappa _\mu \hat a_\mu \hat a_{{{\mathrm{C}}}}^{\dagger} + \kappa _\mu \hat a_\mu ^{\dagger} \hat a_{{{\mathrm{C}}}}$, with the bosonic creation and annihilation operators $\hat a_\mu ,\hat a_\mu ^{\dagger}$ for the spatial modes W, E and A. Replacing the general time parameter t with a spatial propagation coordinate z, the resulting Heisenberg equation of motion reads ${{{\mathrm{i}}}}\partial /\partial z\hat a_\mu = \left[ {\hat H,\hat a_\mu } \right]$. The symmetry of the graph gives rise to a pair of degenerate dark modes²⁸. Their respective bosonic creation operators $\hat D_1^{\dagger} (z)$ and $\hat D_2^{\dagger} (z)$ represent the excitation of either mode and, applied to the vacuum $\left| {{{\mathbf{0}}}} \right\rangle$, generate two dark states, $\left| {d_1\left( z \right)} \right\rangle = \hat D_1^{\dagger} \left| {{{\mathbf{0}}}} \right\rangle$ and $\left| {d_2\left( z \right)} \right\rangle = \hat D_2^{\dagger} \left| {{{\mathbf{0}}}} \right\rangle$. Here, the term ‘dark’ indicates the absence of light in the central mode. Under adiabatic propagation, these states mix in a purely geometric fashion in line with a U(2) quantum holonomy. Note that identifying the actual number of suitable dark states in a bosonic system is a potentially ambiguous task when using the established, purely state-based mathematical description in the Schrödinger picture⁸, as the apparent dimensionality of the zero-energy subspace was consistently found to exceed the actual number of states that can be addressed by a single holonomy³⁰. Whereas the conventional approach directly uses zero-energy states to span the subspace, we fully embrace the second quantization and develop a description based on the bosonic creation operators in the Heisenberg picture. Launching two indistinguishable bosons into the system yields a triplet of possible dark states, $\left| {D_1\left( z \right) } \right\rangle = \frac{1}{{\sqrt 2 }}\hat D_1^{\dagger} \hat D_1^{\dagger} \left| {{{\mathbf{0}}}} \right\rangle$, $\left| {D_2\left( z \right)} \right\rangle = \hat D_1^{\dagger} \hat D_2^{\dagger} \left| {{{\mathbf{0}}}} \right\rangle$, and $\left| {D_3\left( z \right)} \right\rangle = \frac{1}{{\sqrt 2 }}\hat D_2^{\dagger} \hat D_2^{\dagger} \left| {{{\mathbf{0}}}} \right\rangle$, that implement the desired U(3) quantum holonomy. In this vein, our model simplifies the calculation of the dark states of larger Hilbert spaces that can be created by multiple excitations of a given bosonic mode and readily allows one to distinguish them from hybridized zero-energy states that are not suitable for the purpose of increasing the holonomies’ dimensionality (Methods). Note that such scaling of the symmetry group via multiple simultaneous excitations is a feature unique to bosonic systems.

Fig. 2: Synthesizing photonic quantum holonomies.

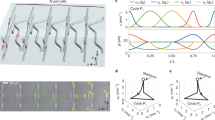
a, A star graph of four modes (west wing W, east wing E, central site C and auxiliary A) is represented by a tripod configuration of photonic waveguides arranged such that interactions mediated by evanescent coupling occur exclusively in the radial direction. b, The strength of these interactions is described by the respective coupling coefficients $\kappa _{{{{\mathrm{W}}}}/{{{\mathrm{E}}}}/{{{\mathrm{A}}}}}$, which span the parameter space ${{{\mathcal{M}}}}$. The desired loop γ (blue) is implemented by parameterizing the couplings along the spatial coordinate $z \in [0,12.0\;{{{\mathrm{cm}}}}]$ which indicates the longitudinal position within the sample. In our setting, $\kappa _{{{\mathrm{W}}}}$ (green) and $\kappa _{{{\mathrm{E}}}}$ (yellow) follow Gaussian profiles with the respective maxima at $z = 4.5\;{{{\mathrm{cm}}}}$ and $z = 7.5\;{{{\mathrm{cm}}}}$, while $\kappa _{{{\mathrm{A}}}}$ is kept constant. c, With $\kappa _{{{\mathrm{W}}}}$ and $\kappa _{{{\mathrm{E}}}}$ vanishing at both ends of the evolution, the dark states at the front and end facet correspond to simple Fock states. Injecting a single photon in either E or W of this arrangement therefore gives rise to a doublet of dark states, $\left| {d_1} \right\rangle$ and $\left| {d_1} \right\rangle$, that instantiate a U(2) holonomy. d, In turn, the triplet of dark states required to construct a U(3) holonomy is obtained by both photons of an indistinguishable pair into either E or W ($\left| {D_1} \right\rangle$ and $\left| {D_3} \right\rangle$, respectively), or one of them in each ($\left| {D_2} \right\rangle$).

In our photonic implementation, the nodes W, E, C and A of the star graph are represented by single-mode waveguides arranged in a tripod geometry (Fig. 2a). In turn, the parameters $(\kappa _\mu )_\mu$ take the form of coupling coefficients, describing the rates at which photons couple evanescently between the central site C and the channels surrounding it. For convenience, $\gamma (z)$ has been chosen such that the system’s dark states are identical to Fock states (Fig. 2c,d) at the initial and final positions $z_{{{{\mathrm{i}}}},{{{\mathrm{f}}}}}$. In other words, at the front and end facets of our chip, the photons of $\left| {d_1} \right\rangle$ and $\left| {d_2} \right\rangle$ are located in waveguide W and E, respectively, allowing for straightforward excitation and detection. The loop $\gamma (z)$ itself is encoded in the spatial trajectories of the outer waveguides that were chosen to realize the appropriate z-dependent separations (Fig. 3a). In a first set of experiments, we characterized the tripod by launching single-photon dark states and subsequently analysed the resulting superposition via heralded single-photon measurements using avalanche photodiodes (APDs) (Fig. 3b). From the output click statistics, the absolute square of the matrix elements of the U(2) holonomy were obtained (Fig. 3c). With an average fidelity of $\bar F$ and similarity of S of 99.7% to the ideal theoretical configuration, these measurements clearly confirm the presence of the underlying U(2) holonomy in the single-photon case.

Fig. 3: Experimental realization of the photonic tripod.

a, In line with an exponential dependence of the coupling on the separation, the driven tripod structure illustrated in Fig. 2a can be translated into a spatial arrangement of laser-written waveguides. In particular, both the C and A channels are chosen to be straight with a constant separation of 18.91 μm, while W and E approach C along parabolic trajectories to a minimum distance of 19.43 μm. To facilitate an efficient coupling to standard fibre arrays with a horizontal pitch of 82.0 μm, transmission-optimized fanning sections (semi-transparent) were appended on both sides of the structure. b, The indistinguishable photons for our experiments are generated by type I spontaneous parametric down-conversion (SPDC) in a bismuth borate crystal pumped by a 407.5 nm continuous-wave diode laser. Collected in two separate fibres, these photons are fed via a single-mode fibre array into the fused silica chip containing the laser-written photonic circuit. On the output side, light is collected by a multimode fibre array, and fibre-integrated 50:50 beam splitters are used to enable the identification of the three two-photon dark states via post-selection coincidence measurement by APDs. c, The performance of the tripod structure as a U(2) holonomy was first characterized by injecting single photons into the single-photon dark states $\left| {d_1} \right\rangle$ and $\left| {d_2} \right\rangle$ and subsequently analysing the resulting output distributions of photons across those states. The observed (top) and calculated (bottom) absolute squares of each matrix element of the U(2) holonomy represent the probabilities of detecting the single-photon dark states, exhibiting an average fidelity and similarity of ${\bar F} = S = 99.7\%$ between theory and measurement. The symmetric experimental error ranges (black cylinders) indicate the Poisson s.d.

Source data

Similar to the dark states $\left| {d_1} \right\rangle$ and $\left| {d_2} \right\rangle$ of the single-photon tripod system, the photon pairs associated with the two-photon dark states $\left| {D_1} \right\rangle$ and $\left| {D_3} \right\rangle$ reside exclusively in waveguides W and E at the input and output facets, respectively. In contrast, however, W and E each contain exactly one of the photons of the extended state $\left| {D_2} \right\rangle$, as illustrated schematically in Fig. 2d. While this latter state can be directly populated by injecting the two indistinguishable photons from our SPDC source into channels W and E, $\left| {D_1} \right\rangle$ and $\left| {D_3} \right\rangle$ require both photons to simultaneously inhabit the same waveguide. We synthesized this excitation condition by leveraging the Hong–Ou–Mandel effect³¹ in a fibre-integrated 50:50 beam splitter placed in front of the photonic chip. The reverse strategy was employed to analyse the output distribution. Here, 50:50 beam splitters were inserted behind the outputs of the W and E channels, allowing for all three dark states to be identified in a post-selection measurement. Taking into account a correction factor of 2 between the detected counts and the dark state probability, a set of five APDs allowed us to determine the probability of detecting dark state $\left| {D_j} \right\rangle$ upon injecting $\left| {D_k} \right\rangle$, that is, the absolute square of each matrix element of the U(3) holonomy (Fig. 4a). The observed performance of the circuit matches the theoretical action of the U(3) holonomic design under ideal, fully adiabatic conditions with $\bar F = S = 99.7\%$.

Fig. 4: Observation of the non-Abelian U(3) quantum holonomy.

a, The localized two-photon dark states $\left| {D_1} \right\rangle$ and $\left| {D_3} \right\rangle$ for the U(3) measurement are synthesized from the indistinguishable photon pairs by leveraging the Hong–Ou–Mandel effect in a 50:50 beam splitter, whereas the extended state was populated by injecting the two photons in waveguides W and E in a synchronized fashion. The observed (left) and calculated (right) absolute squares of the U(3) holonomy’s matrix elements represent the detection probabilities for each dark state at the output facet of the chip. We find an average fidelity and similarity of $\bar F = S = 99.7\%$ between our measurements and the ideal theoretical behaviour. The experimental error ranges (black cylinders) once more indicate the Poisson s.d. as well as the tolerances of the fibre-integrated beam splitters. b, The non-Abelian nature of the observed holonomies is verified through the absolute value of the Wilson loop, which equals the (integer) dimensionality of the setting under Abelian conditions. Both the U(2) holonomy characterized in Fig. 3c and the U(3) holonomy shown in a are genuinely non-Abelian, with $|{{{\mathcal{W}}}}_\gamma ^{{{{\mathrm{U}}}}\left( 2 \right)}| = 1.854 \pm 0.001 < 2$ and $|{{{\mathcal{W}}}}_\gamma ^{{{{\mathrm{U}}}}\left( 3 \right)}| = 2.49 \pm 0.02 < 3$, respectively. The vertical axes have been proportionally scaled to allow for a direct comparison of the relative deviations from the Abelian limit in both cases. For reference, we show the theoretical values of $\left| {{{\mathcal{W}}}}_\gamma \right|$ calculated analytically for ideal adiabatic conditions. Numerical propagation simulations show adiabaticity violations incurred during the propagation through the finite structure to be negligible, with approximately 4% of photons being lost to the C and A channels for the U(2) configuration, and the case of U(3), respectively. The experimental error bars comprise the Poisson s.d. of the observed probabilities and the tolerances of the fibre-integrated beam splitters.

Source data

Finally, we turn to the task of verifying whether the realized holonomies are indeed non-Abelian. The Wilson loop, defined as the trace of a holonomy, ${{{\mathcal{W}}}}_\gamma = {{{\mathrm{Tr}}}}\left[ {\hat U\left( \gamma \right)} \right]$, provides a particularly elegant indicator to this end, as its absolute value coincides with the dimensionality N of the underlying unitary group U(N) for Abelian settings. Any significant deviation from integer values of $|{{{\mathcal{W}}}}_\gamma |$ therefore reliably indicates the genuinely matrix-valued nature of a given holonomy³². As shown in Fig. 4b, our system fulfils this condition both for the U(2) configuration ($|{{{\mathcal{W}}}}_\gamma ^{{{{\mathrm{U}}}}\left( 2 \right)}| = 1.854 \pm 0.001 < 2$) and when being operated in the U(3) regime ($|{{{\mathcal{W}}}}_\gamma ^{{{{\mathrm{U}}}}\left( 3 \right)}| = 2.49 \pm 0.02 < 3$). Notably, our click-type measurements only yield information about the photons’ probability distributions and, as such, remain ambiguous with regard to the sign of the wave function. When evaluating the trace, we therefore employed the respective signs from the theoretical calculation. Crucially, none of the possible sign configurations would yield an integer-valued Wilson loop, unequivocally proving the non-Abelian nature of the system. To quantify the diabatic error incurred during the propagation through the finite structure, we performed a numerical simulation of the photon dynamics. With only approximately 4% of photons ending up in the C and A channels for U(2), and 8% for U(3), the resulting marginal deviation from the ideal adiabatic scenario confirms that the observed non-Abelian characteristics can indeed be retained in realistic waveguide circuits.

In conclusion, we have implemented a three-dimensional non-Abelian quantum holonomy—an element of the symmetry group U(3), prominently known from the theory of the strong interaction. Based on a quantum photonic platform, which allows for a scaling of the holonomy’s dimensionality via the number of bosonic excitations, our experiments provide an avenue towards designing quantum optical analogies to illuminate aspects of quantum chromodynamics and, similarly, may serve as convenient tools for the experimental study of gauge symmetries. The exciting possibilities include the extraction of correlation functions from simulated Wilson loops. In this picture, physical couplings could be leveraged to emulate space–time itself. Furthermore, the realization of exotic loop states¹³, whose existence is predicted by loop quantum gravity, are brought within the reach of laboratory-scale experiments. Beyond these cosmological implications, geometric phases are deeply connected to problems of topology and computer science²². Among many potential applications, the approach presented here may be suitable for tying quantum knots in terms of a holonomic braiding of bosonic world lines¹⁹ in on-chip photonic settings.

Methods

Quantum holonomies

To generalize Berry’s geometric phase⁷ to a holonomy that belongs to the symmetry group⁸ U(N), we consider an iso-degenerate family of Hamiltonians $\left\{ {\hat H\left( \kappa \right)} \right\}_\kappa$ parameterized over a control manifold ${{{\mathcal{M}}}}$. This leads to an N-fold degenerate dark subspace ${{{\mathcal{H}}}}_{{{\mathrm{D}}}} = {{{\mathrm{Span}}}}\left( {\left| {D_a} \right\rangle } \right)$ (that is, the zero-eigenvalue eigenspace). As illustrated schematically in Fig. 1, if a piecewise smooth loop $\gamma :\left[ {t_{{{\mathrm{i}}}},t_{{{\mathrm{f}}}}} \right] \to {{{\mathcal{M}}}}$ is traversed adiabatically, any initially prepared state $\left| {\varPsi (t_{{{\mathrm{i}}}})} \right\rangle$ lying in ${{{\mathcal{H}}}}_{{{\mathrm{D}}}}$ will evolve into a final state $\left| {\varPsi (t_{{{\mathrm{f}}}})} \right\rangle = \hat U\left( \gamma \right)\left| {\varPsi (t_{{{\mathrm{i}}}})} \right\rangle \in {{{\mathcal{H}}}}_{{{\mathrm{D}}}}$. The unitary $\hat U\left( \gamma \right)$ is the sought-after quantum holonomy that emerges from the non-trivial topology (that is, it has non-vanishing curvature) of the parameter space ${{{\mathcal{M}}}}$. Specifically, it can be obtained via the path-ordered integral⁸

$$\begin{array}{*{20}{c}} {\hat U\left( \gamma \right) = {{{\mathcal{P}}}}\exp \left({\mathop {\oint}\limits_\gamma {\hat A}}\right) ,} \end{array}$$

(1)

where $\hat A = \Sigma _\mu \hat A_\mu {{{\mathrm{d}}}}\kappa _\mu$ is the adiabatic connection that mediates the parallel transport of a state vector along the loop $\gamma (t)$. Its components read $\left( {\hat A_\mu } \right)_{jk} = \left\langle {D_k} \right|\partial _\mu \left| {D_j} \right\rangle$ with $\partial _\mu = \partial /\partial \kappa _\mu$. Under a unitary change of basis $\left| {D_k} \right\rangle \to \hat G^{ - 1}\left| {D_k} \right\rangle$, the connection transforms as a proper gauge potential $A_\mu \to \hat G\hat A_\mu \hat G^{ - 1} + \hat G\partial _\mu \hat G^{ - 1}$. It follows from equation (1) that the holonomy transforms in a gauge-covariant manner, that is, $\hat U\left( \gamma \right) \to \hat G\hat U\left( \gamma \right)\hat G^{ - 1}$, thus giving rise to the gauge-invariant Wilson loop⁹ ${{{\mathcal{W}}}}_\gamma = Tr\left[ {\hat U\left( \gamma \right)} \right]$. In particular, the connection $A_\mu$ depends on the chosen gauge as well as the parameterization of the couplings $\kappa _\mu$; the Wilson loop nonetheless deviates from the trivial case ${{{\mathcal{W}}}}_\gamma = {{{\mathrm{dim}}}}({{{\mathcal{H}}}}_{{{\mathrm{D}}}})$ only if the underlying parameter space ${{{\mathcal{M}}}}$ possesses non-vanishing curvature.

To implement this concept, a star graph of modes (Fig. 2a) is realized in a tripod arrangement with evanescently coupled waveguides. In this system, three outer waveguides (west wing W, east wing E and auxiliary A) interact exclusively with a central waveguide C. The respective coupling coefficients $(\kappa _\mu )_\mu$ act as local coordinates for the space ${{{\mathcal{M}}}}$. Employing a tight-binding approach for the paraxial propagation of light, the quantized coupled-mode equations read ${{{\mathrm{i}}}}\partial /\partial z\hat a_\mu = \left[ {\hat H,\hat a_\mu } \right]$, where the system’s Hamiltonian is given by $\hat H = \Sigma _\mu \kappa _\mu \hat a_\mu \hat a_{{{\mathrm{C}}}}^{\dagger} + \kappa _\mu \hat a_\mu ^{\dagger} \hat a_{{{\mathrm{C}}}}.$ Here, $\{ \hat a_\mu ,\hat a_\mu ^{\dagger} \}$ are the bosonic creation and annihilation operators for the spatial mode of the μth waveguide, respectively. The creation operators for the system’s two-fold degenerate dark modes read as $\hat D_1^{\dagger} = \sin \theta \hat a_{{{\mathrm{E}}}}^{\dagger} - \cos \theta \hat a_{{{\mathrm{A}}}}^{\dagger}$ and $\hat D_2^{\dagger} = \cos \varphi \hat a_{{{\mathrm{W}}}}^{\dagger} - \cos \theta \sin \varphi \hat a_{{{\mathrm{E}}}}^{\dagger} - \sin \theta \sin \varphi \hat a_{{{\mathrm{A}}}}^{\dagger}$, whereas its pair of non-degenerate bright modes have the creation operators $\hat B_ \pm ^{\dagger} = \frac{1}{{\sqrt 2 }}\left( {\cos \theta \cos \varphi \hat a_{{{\mathrm{E}}}}^{\dagger} + \sin \theta \cos \varphi \hat a_{{{\mathrm{A}}}}^{\dagger} + \sin \varphi \hat a_{{{\mathrm{W}}}}^{\dagger} \pm \hat a_{{{\mathrm{C}}}}^{\dagger} } \right).$ Here we utilized the parameterization $\theta = \arctan \left( {\kappa _{{{\mathrm{A}}}}/\kappa _{{{\mathrm{E}}}}} \right)$, and $\varphi = \arctan \left( {\kappa _{{{\mathrm{W}}}}/\sqrt {\kappa _{{{\mathrm{E}}}}^2 + \kappa _{{{\mathrm{A}}}}^2} } \right)$ for convenience. These four operators form an orthonormal set, that is, $\left[ {\hat H,\hat D_1^{\dagger} } \right] = \left[ {\hat H,\hat D_2^{\dagger} } \right] = 0$ and $\left[ {\hat H,\hat B_ \pm ^{\dagger} } \right] = \pm \sqrt {\kappa _{{{\mathrm{W}}}}^2 + \kappa _{{{\mathrm{E}}}}^2 + \kappa _{{{\mathrm{A}}}}^2} \hat B_ \pm ^{\dagger}$.

When only a single photon is injected into the four-mode vacuum $\left| {{{\mathbf{0}}}} \right\rangle$, the dark states $\left| {d_1\left( {\theta ,\varphi } \right)} \right\rangle = \hat D_1^{\dagger} \left| {{{\mathbf{0}}}} \right\rangle$ and $\left| {d_2\left( {\theta ,\varphi } \right)} \right\rangle = \hat D_2^{\dagger} \left| {{{\mathbf{0}}}} \right\rangle$ span a two-fold degenerate subspace. The gauge potential for this case is readily found to be $\hat A_\theta = \left( {\begin{array}{*{20}{c}} 0 & { - {{{\mathrm{sin}}}}\varphi } \\ {{{{\mathrm{sin}}}}\varphi } & 0 \end{array}} \right)$ and $\hat A_\varphi = 0$. Under adiabatic propagation, any initial input is transformed²⁸ according to the holonomy $\hat u\left( \gamma \right) = \left( {\begin{array}{*{20}{c}} {\cos \phi } & { - \sin \phi } \\ {\sin \phi } & {\cos \phi } \end{array}} \right)$ with $\phi \left( \gamma \right)$ being a phase factor determined solely by the given loop γ in ${{{\mathcal{M}}}}$.

When a second photon is introduced simultaneously, we find three combinations, $\left| {D_1\left( {\theta ,\varphi } \right)} \right\rangle = \frac{1}{{\sqrt 2 }}\hat D_1^{\dagger} \hat D_1^{\dagger} \left| {{{\mathbf{0}}}} \right\rangle$, $\left| {D_2\left( {\theta ,\varphi } \right)} \right\rangle = \hat D_1^{\dagger} \hat D_2^{\dagger} \left| {{{\mathbf{0}}}} \right\rangle$ and $\left| {D_3\left( {\theta ,\varphi } \right)} \right\rangle = \frac{1}{{\sqrt 2 }}\hat D_2^{\dagger} \hat D_2^{\dagger} \left| {{{\mathbf{0}}}} \right\rangle$, that represent valid two-photon dark states. A straightforward calculation of the gauge potential² for this case reveals $\hat A_\theta = \left( {\begin{array}{*{20}{c}} 0 & { - \sqrt 2 {{{\mathrm{sin}}}}\varphi } & 0 \\ {\sqrt 2 {{{\mathrm{sin}}}}\varphi } & 0 & { - \sqrt 2 {{{\mathrm{sin}}}}\varphi } \\ 0 & {\sqrt 2 {{{\mathrm{sin}}}}\varphi } & 0 \end{array}} \right)$ and $\hat A_\varphi = 0$, from which the holonomy can be obtained by direct evaluation of the matrix exponential^30,33

$$\begin{array}{*{20}{c}} {\hat U\left( \gamma \right) = \left( {\begin{array}{*{20}{c}} {\cos \left( \phi \right)^2} & { - \sqrt 2 \sin \phi \cos \phi } & {\sin \left( \phi \right)^2} \\ {\sqrt 2 \sin \phi \cos \phi } & {\cos \left( {2\phi } \right)} & { - \sqrt 2 \sin \phi \cos \phi } \\ {\sin \left( \phi \right)^2} & {\sqrt 2 \sin \phi \cos \phi } & {\cos \left( \phi \right)^2} \end{array}} \right).} \end{array}$$

(2)

In contrast to the case where only a single photon is injected, this holonomy belongs to the symmetry group U(3). This means, under a unitary mixing of all three dark states $\left| {D_j} \right\rangle \to \hat G\left| {D_j} \right\rangle$, the unitary $\hat U\left( \gamma \right)$ transforms covariantly as $\hat G\hat U\left( \gamma \right)\hat G^{ - 1}$. Here, $\hat G$ denotes an arbitrary unitary 3 × 3 matrix, that is, $\hat G \in {{{\mathrm{U}}}}(3)$. For instance, we choose a particular starting configuration $\kappa _{{{\mathrm{A}}}}(z_{{{\mathrm{i}}}}) = {{{\mathrm{const}}}}$, $\kappa _{{{\mathrm{W}}}}(z_{{{\mathrm{i}}}}) = \kappa _{{{\mathrm{E}}}}(z_{{{\mathrm{i}}}}) = 0$, such that the dark states $\left| {D_j(z_{{{\mathrm{i}}}})} \right\rangle$ reduce to simple Fock states. However, if the initial coupling was chosen differently, the initial dark states would be superpositions of the form $\hat G\left| {D_j(z_{{{\mathrm{i}}}})} \right\rangle$. Even though the holonomy appears to be quite different in this gauge, measurement results remain unchanged:

$$\left\langle {D_j\left( {z_{{{\mathrm{i}}}}} \right)} \right|\hat G^{ - 1}\hat G\hat U\left( \gamma \right)\hat G^{ - 1}\hat G\left| {D_j\left( {z_{{{\mathrm{i}}}}} \right)} \right\rangle = \left\langle {D_j\left( {z_{{{\mathrm{i}}}}} \right)} \right|\hat U\left( \gamma \right)\left| {D_j\left( {z_{{{\mathrm{i}}}}} \right)} \right\rangle .$$

(3)

In contrast, in the Abelian case, $\hat G$ reduces to merely a global phase, thus the corresponding holonomy would be a manifestly gauge-invariant quantity. Identifying the actual number of states that are suitable to construct holonomies in a bosonic system has proven to be an ambiguous task when using the established, purely state-based mathematical description in the Schrödinger picture, as the apparent dimensionality of the dark subspace was consistently found to exceed the actual number of states that could be addressed by a single holonomy³⁰. Our mathematical description relying on bosonic creation operators allows us to clearly identify the ‘genuine’ dark states of a system and to distinguish them from hybridized zero-energy states that also fall within the scope of the original definition⁸ of the term. For the case in point, the structure of the star graph on which our tripod is based gives rise to one such ‘phantom’ dark state, $\hat B_ + ^{\dagger} \hat B_ - ^{\dagger} \left| {{{\mathbf{0}}}} \right\rangle$, whose eigenenergy is pinned to zero due to $\left[ {\hat H,\hat B_ + ^{\dagger} \hat B_ - ^{\dagger} } \right] = 0$. Yet, by virtue of the non-degenerate nature of its constituent bright modes, this state remains unaffected by the holonomy and therefore cannot be employed to further increase its dimensionality. Our description of holonomies in the Heisenberg model removes any previous ambiguities and thus serves to streamline the process of determining the dimensionality of the holonomy, even when the number of indistinguishable photons is increased well beyond two. Along these lines, we propose a more restrictive definition of the term ‘dark state’ to refer only to states that are created exclusively by exciting dark modes.

Experimental platform and sample design

For the experimental realization, the path γ in ${{{\mathcal{M}}}}$ was chosen such that $\kappa _{{{\mathrm{W}}}}(z)$ and $\kappa _{{{\mathrm{E}}}}(z)$ change in Gaussian fashion during the propagation, $\kappa _{{{{\mathrm{E}}}},{{{\mathrm{W}}}}}\left( z \right) = {{\Omega }}\exp \left[ { - \frac{{\left( {z - \bar z \pm \tau } \right)^2}}{{T^2}}} \right]$, while $\kappa _{{{\mathrm{A}}}}(z)$ remains constant. In addition, this type of path ensures vanishing couplings $\kappa _{{{\mathrm{W}}}}$ and $\kappa _{{{\mathrm{E}}}}$ at both $z_{{{\mathrm{i}}}}$ and $z_{{{\mathrm{f}}}}$, which leads to the dark states at the front and end facet being simple Fock states. To ensure an adiabatic propagation while accounting for the experimentally accessible parameter ranges and steering clear of a trivial holonomy (that is, $\hat U\left( \gamma \right) \ne \hat 1$), an optimization process based on the quantum metric was employed²⁸, yielding the parameters: $\kappa _{{{\mathrm{A}}}} = 1.1\,{{{\mathrm{cm}}}}^{ - 1}$, ${{\Omega }} = 0.9\,{{{\mathrm{cm}}}}^{ - 1}$, $\tau = 1.5\,{{{\mathrm{cm}}}}$, $T = 2.5\,{{{\mathrm{cm}}}}$, $\bar z = 6\,{{{\mathrm{cm}}}}$ and $z \in \left[ {0,2\bar z} \right]$. Consequently, the phase factor $\phi \left( \gamma \right)$ that determines the holonomy (equation (2)) takes the value $\phi \left( \gamma \right) \approx 0.33$. Translating the couplings $\kappa _\mu$ into real-space distances yields the three-dimensional waveguide arrangement depicted in Fig. 3a. Using the femtosecond-laser direct writing technique³⁴, the design was inscribed into the volume of a fused silica chip (Corning 7980) and subsequently studied using indistinguishable photons from a type I SPDC source.

To quantitatively assess the performance of the circuit, we compared the experimental data against the theoretical predictions of the ideal closed loop in terms of the average fidelity as well as a generalization of this measure, the similarity. The fidelity is defined as $F = \left| {\left\langle {\psi _{{{{\mathrm{out}}}}}^{{{{\mathrm{theo}}}}}{{{\mathrm{|}}}}\psi _{{{{\mathrm{out}}}}}^{{{{\mathrm{exp}}}}}} \right\rangle } \right|^2$, where $\left| {\psi _{{{{\mathrm{out}}}}}^{{{{\mathrm{theo}}}}/{{{\mathrm{exp}}}}}} \right\rangle$ denote the theoretical and experimental output states, respectively. Expanding the output states as $\left| {\psi _{{{{\mathrm{out}}}},k}^{{{{\mathrm{theo}}}}/{{{\mathrm{exp}}}}}} \right\rangle = \mathop {\sum }\limits_{j = 1:N} \sqrt {p_{kj}^{{{{\mathrm{theo}}}}/{{{\mathrm{exp}}}}}} \left| {D_j(z_{{{\mathrm{f}}}})} \right\rangle$ and averaging over all prepared input states yields the average fidelity $\bar F = \frac{1}{N}\mathop {\sum }\nolimits_{j = 1:N} \left( {\mathop {\sum }\nolimits_{k = 1:N} \sqrt {p_{kj}^{{{{\mathrm{theo}}}}}p_{kj}^{{{{\mathrm{exp}}}}}} } \right)^2$ (also known as the Bhattacharyya distance)³⁵, where the orthogonality of dark states ($\left\langle {D_k(z_{{{\mathrm{f}}}}){{{\mathrm{|}}}}D_j(z_{{{\mathrm{f}}}})} \right\rangle = \delta _{jk}$) was used and $p_{kj}^{{{{\mathrm{exp}}}}/{{{\mathrm{theo}}}}}$ stand for the probability of detecting dark state $\left| {D_j} \right\rangle$ after preparing $\left| {D_k} \right\rangle$ in the experiment or theoretical calculation, respectively. The similarity, as a generalization of the average fidelity, is defined as $S = \left( {\mathop {\sum }\nolimits_{\,j,k = 1:N} \sqrt {p_{kj}^{{{{\mathrm{theo}}}}}p_{kj}^{{{{\mathrm{exp}}}}}} } \right)^2/\mathop {\sum }\nolimits_{j,k = 1:N} p_{kj}^{{{{\mathrm{theo}}}}}\mathop {\sum }\nolimits_{k,\,j = 1:N} p_{kj}^{{{{\mathrm{exp}}}}}$ (ref. ³⁶). All quantities provided were rounded to one significant digit according to National Institute of Standards and Technology rounding method GLP 9-A³⁷.