Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Active phase separation by turning towards regions of higher density

Nature Physics volume 17, pages 961–967 (2021)Cite this article

Subjects

Abstract

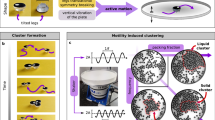
Studies of active matter, from molecular assemblies to animal groups, have revealed two broad classes of behaviour: a tendency to align yields orientational order and collective motion, whereas particle repulsion leads to self-trapping and motility-induced phase separation. Here we report a third class of behaviour: orientational interactions that produce active phase separation. Combining theory and experiments on self-propelled Janus colloids, we show that stronger repulsion on the rear than on the front of these particles produces non-reciprocal torques that reorient particle motion towards high-density regions. Particles thus self-propel towards crowded areas, which leads to phase separation. Clusters remain fluid and exhibit fast particle turnover, in contrast to the jammed clusters that typically arise from self-trapping, and interfaces are sufficiently wide that they span entire clusters. Overall, our work identifies a torque-based mechanism for phase separation in active fluids, and our theory predicts that these orientational interactions yield coexisting phases that lack internal orientational order.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Active phase separation in metal–dielectric Janus colloids.
Fig. 2: Particle turnover dynamics of non-jammed clusters whose population remains nearly constant.
Fig. 3: Particle orientation, velocity and correlations in non-jammed clusters.
Fig. 4: State diagram of torque-based active phase separation.

Similar content being viewed by others

Data availability

Source data are provided with this paper. All other data that support the plots and findings of this study are available from the authors upon request.

Code availability

All codes are available from the authors upon request.

References

  1. Cates, M. E. & Tailleur, J. Motility-induced phase separation. Annu. Rev. Condens. Matter Phys. 6, 219–244 (2015).

    Article  ADS  Google Scholar 

  2. Gonnella, G., Marenduzzo, D., Suma, A. & Tiribocchi, A. Motility-induced phase separation and coarsening in active matter. C. R. Phys. 16, 316–331 (2015).

    Article  Google Scholar 

  3. Marchetti, M. C., Fily, Y., Henkes, S., Patch, A. & Yllanes, D. Minimal model of active colloids highlights the role of mechanical interactions in controlling the emergent behavior of active matter. Curr. Opin. Colloid Interface Sci. 21, 34–43 (2016).

    Article  Google Scholar 

  4. Zöttl, A. & Stark, H. Emergent behavior in active colloids. J. Phys. Condens. Matter 28, 253001 (2016).

    Article  ADS  Google Scholar 

  5. Speck, T. Collective forces in scalar active matter. Soft Matter 16, 2652–2663 (2020).

    Article  ADS  Google Scholar 

  6. Ma, Z., Yang, M. & Ni, R. Dynamic assembly of active colloids: theory and simulation. Adv. Theory Simul. 3, 2000021 (2020).

    Article  Google Scholar 

  7. Tailleur, J. & Cates, M. E. Statistical mechanics of interacting run-and-tumble bacteria. Phys. Rev. Lett. 100, 218103 (2008).

    Article  ADS  Google Scholar 

  8. Rein, M., Heinß, N., Schmid, F. & Speck, T. Collective behavior of quorum-sensing run-and-tumble particles under confinement. Phys. Rev. Lett. 116, 058102 (2016).

    Article  ADS  Google Scholar 

  9. Fily, Y. & Marchetti, M. C. Athermal phase separation of self-propelled particles with no alignment. Phys. Rev. Lett. 108, 235702 (2012).

    Article  ADS  Google Scholar 

  10. Redner, G. S., Hagan, M. F. & Baskaran, A. Structure and dynamics of a phase-separating active colloidal fluid. Phys. Rev. Lett. 110, 055701 (2013).

    Article  ADS  Google Scholar 

  11. Bialké, J., Löwen, H. & Speck, T. Microscopic theory for the phase separation of self-propelled repulsive disks. Europhys. Lett. 103, 30008 (2013).

    Article  ADS  Google Scholar 

  12. Aranson, I. S. Active colloids. Phys. Usp. 56, 79–92 (2013).

    Article  ADS  Google Scholar 

  13. Bechinger, C. et al. Active particles in complex and crowded environments. Rev. Mod. Phys. 88, 045006 (2016).

    Article  ADS  MathSciNet  Google Scholar 

  14. Zhang, J., Luijten, E., Grzybowski, B. A. & Granick, S. Active colloids with collective mobility status and research opportunities. Chem. Soc. Rev. 46, 5551–5569 (2017).

    Article  Google Scholar 

  15. Theurkauff, I., Cottin-Bizonne, C., Palacci, J., Ybert, C. & Bocquet, L. Dynamic clustering in active colloidal suspensions with chemical signaling. Phys. Rev. Lett. 108, 268303 (2012).

    Article  ADS  Google Scholar 

  16. Palacci, J., Sacanna, S., Steinberg, A. P., Pine, D. J. & Chaikin, P. M. Living crystals of light-activated colloidal surfers. Science 339, 936–940 (2013).

    Article  ADS  Google Scholar 

  17. Buttinoni, I. et al. Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles. Phys. Rev. Lett. 110, 238301 (2013).

    Article  ADS  Google Scholar 

  18. Ginot, F., Theurkauff, I., Detcheverry, F., Ybert, C. & Cottin-Bizonne, C. Aggregation–fragmentation and individual dynamics of active clusters. Nat. Commun. 9, 696 (2018).

    Article  ADS  Google Scholar 

  19. Geyer, D., Martin, D., Tailleur, J. & Bartolo, D. Freezing a flock: motility-induced phase separation in polar active liquids. Phys. Rev. X 9, 031043 (2019).

    Google Scholar 

  20. van der Linden, M. N., Alexander, L. C., Aarts, D. G. A. L. & Dauchot, O. Interrupted motility induced phase separation in aligning active colloids. Phys. Rev. Lett. 123, 098001 (2019).

    Article  ADS  Google Scholar 

  21. Shi, X.-q. & Chaté, H. Self-propelled rods: linking alignment-dominated and repulsion-dominated active matter. Preprint at https://arxiv.org/abs/1807.00294 (2018).

  22. van Damme, R., Rodenburg, J., van Roij, R. & Dijkstra, M. Interparticle torques suppress motility-induced phase separation for rodlike particles. J. Chem. Phys. 150, 164501 (2019).

    Article  ADS  Google Scholar 

  23. Jayaram, A., Fischer, A. & Speck, T. From scalar to polar active matter: connecting simulations with mean-field theory. Phys. Rev. E 101, 022602 (2020).

    Article  ADS  Google Scholar 

  24. Großmann, R., Aranson, I. S. & Peruani, F. A particle–field approach bridges phase separation and collective motion in active matter. Nat. Commun. 11, 5365 (2020).

    Article  ADS  Google Scholar 

  25. Bär, M., Großmann, R., Heidenreich, S. & Peruani, F. Self-propelled rods: insights and perspectives for active matter. Annu. Rev. Condens. Matter Phys. 11, 441–466 (2020).

    Article  Google Scholar 

  26. Pu, M., Jiang, H. & Hou, Z. Reentrant phase separation behavior of active particles with anisotropic Janus interaction. Soft Matter 13, 4112–4121 (2017).

    Article  ADS  Google Scholar 

  27. Liao, G.-J., Hall, C. K. & Klapp, S. H. L. Dynamical self-assembly of dipolar active Brownian particles in two dimensions. Soft Matter 16, 2208–2223 (2020).

    Article  ADS  Google Scholar 

  28. Farrell, F. D. C., Marchetti, M. C., Marenduzzo, D. & Tailleur, J. Pattern formation in self-propelled particles with density-dependent motility. Phys. Rev. Lett. 108, 248101 (2012).

    Article  ADS  Google Scholar 

  29. Barré, J., Chétrite, R., Muratori, M. & Peruani, F. Motility-induced phase separation of active particles in the presence of velocity alignment. J. Stat. Phys. 158, 589–600 (2014).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  30. Sesé-Sansa, E., Pagonabarraga, I. & Levis, D. Velocity alignment promotes motility-induced phase separation. Europhys. Lett. 124, 30004 (2018).

    Article  ADS  Google Scholar 

  31. Bhattacherjee, B. & Chaudhuri, D. Re-entrant phase separation in nematically aligning active polar particles. Soft Matter 15, 8483–8495 (2019).

    Article  ADS  Google Scholar 

  32. Gangwal, S., Cayre, O. J., Bazant, M. Z. & Velev, O. D. Induced-charge electrophoresis of metallodielectric particles. Phys. Rev. Lett. 100, 058302 (2008).

    Article  ADS  Google Scholar 

  33. Moran, J. L. & Posner, J. D. Phoretic self-propulsion. Annu. Rev. Fluid Mech. 49, 511–540 (2017).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  34. Yan, J. et al. Reconfiguring active particles by electrostatic imbalance. Nat. Mater. 15, 1095–1099 (2016).

    Article  ADS  Google Scholar 

  35. Poncet, A., Bénichou, O., Démery, V. & Nishiguchi, D. Pair correlation of dilute active Brownian particles: from low-activity dipolar correction to high-activity algebraic depletion wings. Phys. Rev. E 103, 012605 (2021).

    Article  ADS  Google Scholar 

  36. Kirkwood, J. G., Buff, F. P. & Green, M. S. The statistical mechanical theory of transport processes. III. The coefficients of shear and bulk viscosity of liquids. J. Chem. Phys. 17, 988–994 (1949).

    Article  ADS  Google Scholar 

  37. Irving, J. H. & Kirkwood, J. G. The statistical mechanical theory of transport processes. IV. The equations of hydrodynamics. J. Chem. Phys. 18, 817–829 (1950).

    Article  ADS  MathSciNet  Google Scholar 

  38. Fruchart, M., Hanai, R., Littlewood, P. B. & Vitelli, V. Non-reciprocal phase transitions. Nature 592, 363–369 (2021).

    Article  ADS  Google Scholar 

  39. Barberis, L. & Peruani, F. Large-scale patterns in a minimal cognitive flocking model: incidental leaders, nematic patterns, and aggregates. Phys. Rev. Lett. 117, 248001 (2016).

    Article  ADS  Google Scholar 

  40. Durve, M., Saha, A. & Sayeed, A. Active particle condensation by non-reciprocal and time-delayed interactions. Eur. Phys. J. E 41, 49 (2018).

    Article  Google Scholar 

  41. Lavergne, F. A., Wendehenne, H., Bäuerle, T. & Bechinger, C. Group formation and cohesion of active particles with visual perception-dependent motility. Science 364, 70–74 (2019).

    Article  ADS  Google Scholar 

  42. Stenhammar, J., Tiribocchi, A., Allen, R. J., Marenduzzo, D. & Cates, M. E. Continuum theory of phase separation kinetics for active Brownian particles. Phys. Rev. Lett. 111, 145702 (2013).

    Article  ADS  Google Scholar 

  43. Wittkowski, R. et al. Scalar ϕ4 field theory for active-particle phase separation. Nat. Commun. 5, 4351 (2014).

    Article  ADS  Google Scholar 

  44. Speck, T., Bialké, J., Menzel, A. M. & Löwen, H. Effective Cahn–Hilliard equation for the phase separation of active Brownian particles. Phys. Rev. Lett. 112, 218304 (2014).

    Article  ADS  Google Scholar 

  45. Speck, T., Menzel, A. M., Bialké, J. & Löwen, H. Dynamical mean-field theory and weakly non-linear analysis for the phase separation of active Brownian particles. J. Chem. Phys. 142, 224109 (2015).

    Article  ADS  Google Scholar 

  46. Paliwal, S., Rodenburg, J., van Roij, R. & Dijkstra, M. Chemical potential in active systems: predicting phase equilibrium from bulk equations of state? New J. Phys. 20, 015003 (2018).

    Article  ADS  Google Scholar 

  47. Solon, A. P., Stenhammar, J., Cates, M. E., Kafri, Y. & Tailleur, J. Generalized thermodynamics of phase equilibria in scalar active matter. Phys. Rev. E 97, 020602 (2018).

    Article  ADS  Google Scholar 

  48. Solon, A. P., Stenhammar, J., Cates, M. E., Kafri, Y. & Tailleur, J. Generalized thermodynamics of motility-induced phase separation: phase equilibria, Laplace pressure, and change of ensembles. New J. Phys. 20, 075001 (2018).

    Article  ADS  Google Scholar 

  49. Marchetti, M. C. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013).

    Article  ADS  Google Scholar 

  50. Hagan, M. F. & Baskaran, A. Emergent self-organization in active materials. Curr. Opin. Cell Biol. 38, 74–80 (2016).

    Article  Google Scholar 

  51. Fodor, É. & Marchetti, M. C. The statistical physics of active matter: from self-catalytic colloids to living cells. Physica A 504, 106–120 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  52. Shaebani, M. R., Wysocki, A., Winkler, R. G., Gompper, G. & Rieger, H. Computational models for active matter. Nat. Rev. Phys. 2, 181–199 (2020).

    Article  Google Scholar 

Download references

Acknowledgements

J.Z. and S.G. were supported by the taxpayers of South Korea through the Institute of Basic Science, project code IBS-R020-D1. R.A. thanks J. Tailleur for insightful discussions, and acknowledges discussions with the participants of the virtual ‘Active 20’ KITP programme, supported in part by the National Science Foundation under grant no. NSF PHY-1748958. R.A. acknowledges support from the Human Frontier Science Program (LT000475/2018-C). J.Y. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund. N.S.W. acknowledges support from the National Science Foundation, through the Center for the Physics of Biological Function (PHY-1734030).

Author information

Author notes

  1. These authors contributed equally: Jie Zhang, Ricard Alert.

Authors and Affiliations

  1. Department of Physics, University of California at Santa Barbara, Santa Barbara, CA, USA

    Jie Zhang

  2. Lewis-Sigler Institute for Integrative Genomics, Princeton University, Princeton, NJ, USA

    Ricard Alert & Ned S. Wingreen

  3. Princeton Center for Theoretical Science, Princeton University, Princeton, NJ, USA

    Ricard Alert

  4. Department of Molecular, Cellular and Developmental Biology, Yale University, New Haven, CT, USA

    Jing Yan

  5. Department of Molecular Biology, Princeton University, Princeton, NJ, USA

    Ned S. Wingreen

  6. Center for Soft and Living Matter, Institute for Basic Science (IBS), Ulsan, South Korea

    Steve Granick

  7. Departments of Chemistry and Physics, Ulsan National Institute of Science and Technology (UNIST), Ulsan, South Korea

    Steve Granick

Authors
  1. Jie Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ricard Alert
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jing Yan
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Ned S. Wingreen
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Steve Granick
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

J.Z., J.Y. and S.G. conceived the experiment. J.Z. performed the experiments and analysed data with help from J.Y. R.A. conceived and developed the theory and analysed data. N.S.W. supervised the theory. All authors discussed and interpreted the results. J.Z., R.A., N.S.W. and S.G. wrote the manuscript.

Corresponding author

Correspondence to Steve Granick.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Peer review information Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Ostwald ripening of active colloids.

Series of snapshots showing a small cluster shrinking and disappearing as part of the coarsening process.

Extended Data Fig. 2 Clusters with and without stuck particles.

a, A bright field microscopy image of active phase separation in a late stage with yellow stars labelling particles that, stuck to the coverslip, remain in the same location throughout the experiment. b, The number (magenta) and fraction (blue) of clusters with and without (solid and dotted curves, respectively) at least one stuck particle. In the beginning of the experiment, more clusters are formed without than with stuck particles. With elapsed time, the number of clusters forming both with and without stuck particles decreases (magenta), but clusters with stuck particles become the most abundant.

Source data

Extended Data Fig. 3 Dynamics of cluster growth.

a, Snapshots of cluster growth upon a.c. electric field application (Supplementary Movie 2). Scale bar, 100 μm. The yellow circumference indicates the outline of the cluster in the final snapshot. b, Density profile evolution in the growing cluster shown in a. Averages are over 20 frames (1.2 s) centered at each designated time point. Error bars are s.d.

Source data

Extended Data Fig. 4 Particle-number fluctuations in a quasi-steady state cluster.

The number of particles in this cluster, the same cluster also shown in Figs. 1 and 2, remains roughly constant during the time when averages are taken.

Source data

Extended Data Fig. 5 Particle turnover time depends on cluster size and particle speed.

The turnover time τ, defined in Fig. 2b, depends on the number of particles N in the cluster, and on particle speed and interactions. The number of particles is averaged over the time used to calculate the turnover time τ as in Fig. 2b. This averaging time varies from 30 to 180 s in different clusters. Error bars are s.d. Blue points correspond to an applied electric field with amplitude 66 V/mm and frequency 30 kHz, producing an average single-particle speed of 12 μm/s within clusters. Red points correspond to a field with the same frequency but amplitude 83 V/mm, giving an average single-particle speed of 22 μm/s within clusters. Particles with higher speeds and stronger interactions turn over more quickly.

Source data

Extended Data Fig. 6 Mean square displacements.

Mean square displacements of particle position (a) and angle (b) for particles at different local area fractions ϕ. The particle speed and effective rotational diffusivity shown in Fig. 2c are obtained from the first 0.5 s of these data by fitting MSD = (vt)2 and MSAD = D\({}_{{\rm{r}}}^{{\rm{eff}}}t\), respectively.

Source data

Extended Data Fig. 7 Orientation-velocity coincidence prior to clustering.

Joint probability distribution function (PDF) of the particle orientation and velocity angles, as defined in Fig. 3d, prior to cluster formation. In contrast to the mismatch found in clusters (Figs. 3e and 3f), the orientation and velocity directions coincide before clusters form.

Extended Data Fig. 8 Dynamics and statistics of two-particle interaction events.

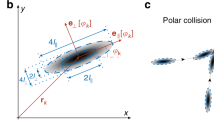
a,b, Two examples of interaction events between two particles, which we define by the condition r12 < 3R, with R the particle radius. We also require the minimal interparticle distance to be min r12 < 2.2R. We analyzed 2061 of such interaction events. In a, both particles turn clockwise. Therefore, the interaction torque has the same sign on both particles, showing that torques are non-reciprocal (Γ12 ≠ -Γ21). This type of interaction with particles initially pointing in opposite directions, defined by the condition ∣θ1(t = 0) + θ2(t = 0)∣ < 0.2 rad, occurred in ~33% of the analyzed events. In b, particle 1 changes its orientation very little compared to particle 2, showing another example of non-reciprocal torques. The particles end up aligned in a chain. This type of interaction, defined by the condition \(\min ({\theta }_{1}({\rm{t}})-{\theta }_{2}({\rm{t}}))<0.5\) rad during the interaction event, occurred in ~2.8% of the analyzed events. c,d, Evolution of the interparticle distance, r12, and the change in angle of each particle, Δθ1,2, for the interaction events in a and b, respectively. e,f, Joint probability distribution functions of the angle changes of each particle in an interacting pair. The pre-collision (e) and post-collision (f) phases respectively correspond to the times before and after the particles reach their minimal distance. These histograms show that, statistically, both particles in the interacting pair tend to turn in the same direction, showing that interaction torques are non-reciprocal. Reciprocal torques would lead to particles rotating in opposite directions and by the same magnitude, as indicated by the dashed lines.

Source data

Extended Data Fig. 9 Pair distribution function measured in experiments.

a, Full g(x, y) used in the calculation of the collective force and torque coefficients ζ0, ζ1, and τ1 (see text and Supplementary Eq. (37)). b, Zoomed-in region, which allows to more clearly appreciate that the pair distribution function is anisotropic, indicating that it is more likely to find another particle in front than behind a reference self-propelled particle. In each panel, the arrow indicates the direction of self-propulsion of the reference particle, dashed lines indicate the coordinate axes, and the white circle indicates the region r < 2R of volume exclusion between two particles.

Extended Data Fig. 10 Effective thermodynamics of torque-based MIPS.

Effective free energy density (a, Supplementary Eq. (56)), chemical potential (b, Supplementary Eq. (55)), and thermodynamic pressure (c–d, Supplementary Eq. (57)) of the active Janus suspension as a function of the area fraction of particles, for v0 = 10 μm/s. The remaining parameter values are evaluated using the estimates in Table I in the Supplementary Note. To better visualize the double-well shape of the free energy βf(ϕ), we added a linear term − 16.5ϕ, which does not affect phase coexistence. Thin dashed lines indicate the densities of the coexisting phases. These densities are obtained from the common-tangent construction on the free energy density (a), which corresponds to equality of both chemical potential (b) and pressure (c), as indicated by thick dashed lines. Alternatively, the common-tangent construction also corresponds to the Maxwell construction on the curve p(1/ϕ), as indicated by the thick dashed line in panel d.

Supplementary information

Supplementary Information

Supplementary Notes, Discussion, Fig. 1 and Table 1.

Supplementary Video 1

Coarsening dynamics during active phase separation. This video, taken with a ×5 objective, shows the phase-separation process of a quasi-two-dimensional Janus particle system (ϕ ≈ 0.12) when a.c. electric field (30 kHz, 83 V mm−1) perpendicular to the imaging plane is applied. The video is played at 10× real speed.

Supplementary Video 2

Growth of a representative active cluster. This video, from which the snapshots in Extended Data Fig. 3 are taken, is obtained using a perpendicular a.c. electric field (30 kHz, 83 V mm−1), and is played at 20× real speed.

Supplementary Video 3

Particle turnover dynamics for an active cluster whose population remains nearly constant. The video is taken after the perpendicular a.c. electric field (30 kHz, 67 V mm−1) has been applied for a few minutes and the clusters are coarsening. Particles are colour-coded according to their distance from the cluster centroid in the first frame, which is an arbitrary time point. Particles joining the cluster after the first frame are not labelled. This video is played at 2× real speed and associated with Fig. 2.

Supplementary Video 4

Particle turnover dynamics for two clusters of different sizes. The plots on the right refer to the videos on the left. Native particles are defined as those particles within the frame at the beginning of the video. N0(t) is the number of native particles remaining in the frame after time t. Both videos are taken after the perpendicular a.c. electric field (30 kHz, 67 V mm−1) has been applied for a few minutes. Particles are colour-coded according to their distance from the cluster centroid in the first frame, which is an arbitrary time point. Particles joining the cluster after the first frame are not labelled. This video is played at 2× real speed.

Supplementary Video 5

Flickering chains in an active cluster. Lines are drawn to connect pairs of particles whose centres are separated by less than 3R (R = 1.5 μm), colour-coded by the degree of pair alignment, with red indicating alignment and blue anti-alignment. This video is played at 0.2× real speed. A snapshot of this video is presented in Fig. 3a.

Supplementary Video 6

High-density uniform phase with transient particle chains. This video, taken with a ×20 objective, shows the high-density uniform phase (ϕ ≈ 0.35) with transient particle chains when an a.c. electric field (30 kHz, 83 V mm−1) perpendicular to the imaging plane is applied.

Source data

Source Data Fig. 1

Statistical source data.

Source Data Fig. 2

Statistical source data.

Source Data Fig. 3

Statistical source data.

Source Data Fig. 4

Statistical source data.

Source Data Extended Data Fig. 2

Statistical source data.

Source Data Extended Data Fig. 3

Statistical source data.

Source Data Extended Data Fig. 4

Statistical source data.

Source Data Extended Data Fig. 5

Statistical source data.

Source Data Extended Data Fig. 6

Statistical source data.

Source Data Extended Data Fig. 8

Statistical source data.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, J., Alert, R., Yan, J. et al. Active phase separation by turning towards regions of higher density. Nat. Phys. 17, 961–967 (2021). https://doi.org/10.1038/s41567-021-01238-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-021-01238-8

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing