Introduction

The concept of optimal experimental design, within the overall framework of Bayesian optimization (BO), has been put forward as a design strategy to circumvent the limitations of traditional (costly) exploration of (arbitrary) design spaces. BO utilizes a flexible surrogate model to stochastically approximate the (generally) expensive objective function. This surrogate, in turn, undergoes Bayesian updates as new information about the design space is acquired, according to a predefined acquisition policy. The use of a Bayesian surrogate model does not impose any a priori restrictions (such as concavity or convexity) on the objective function. It was mainly introduced by Mockus1 and Kushner2 and pioneered by Jones et al.3, who developed a framework that balanced the need to exploit available knowledge of the design space with the objective to explore it by using a metric or policy that selects the best next experiment to carry out with the end-goal of accelerating the iterative design process. Multiple extensions have been developed to make the algorithm more efficient4,5,6,7. This popular tool has been successfully used in a wide range of applications8,9. Extensive surveys of this method and its applications can also be found10,11,12.

Materials discovery (MD) can be mapped to an optimization problem in which the goal is to maximize or minimize some desired properties of a material by varying certain features/structural motifs that are ultimately controlled by changing the overall chemistry and processing conditions. A typical task in MD is to predict the material properties based on a collection of features and then use such predictions in an inverse manner to identify the specific set of features leading to a desired, optimal performance. The major goal is then to identify how to search the complex material space spanning the elements in the periodic table, arranged in a virtually infinite number of possible configurations and microstructures, as generated by arbitrary synthesis/processing methods, to meet the target properties. Recently, a design paradigm has been proposed—optimal experimental design—built upon the foundation of BO13,14,15,16,17,18, which seeks to circumvent the limits of traditional (costly) exploration of the materials design space. Early examples were demonstrated by Frazier and Wang19, who took into account both the need to harness the knowledge that exists about the design space and the goal of exploring and identifying the best experiment to speed up the iterative design process. The other important task, other than discovering the target position in the space, is the identification of the key factors responsible for most of the variance in the properties of interest during MD20,21,22. This helps us better understand the underlying physical/chemical mechanisms controlling the properties or phenomena of interest, which in turn results in better strategies for MD and design17,23. There have been several follow-up papers, mainly extending the algorithm in different applied directions13,14,15.

The BO algorithm consists of two major components10,12: (i) modeling a (potentially) high-dimensional black-box function, f, as a surrogate of the (expensive-to-query) objective function, and (ii) optimizing the selected criterion considering uncertainty based on the posterior distribution of f to obtain the design points in the feature space Ω. In the procedure, we repeat the two steps until we satisfy the stopping criteria or, as it is often the case in experimental settings, we exhaust the resources available. A critical aspect of BO is the choice of the probabilistic surrogate model used to fit f. A Gaussian process (GP) is the typical choice, as it is a powerful stochastic interpolation method that is distinguished from others by its mathematical explicitness and computational flexibility, and with straightforward uncertainty quantification, which makes it broadly applicable to many problems12,13,24.

Oftentimes, stationary or isotropic GP-based BO may be challenging when faced with (even moderately) high-dimensional design spaces, particularly when very little initial information about the design space is available—in some fields of science and engineering where BO is being used14,25,26, data sparsity is, in fact, the norm, rather than the exception. In MD problems, data sparsity is exacerbated by the (apparent) high dimensionality of the design space, as a priori, it is possible that many controllable features could be responsible for the materials’ behavior/property of interest. In practice, however, the potentially high-dimensional MD space may actually be reduced, as in materials science it is often the case that a small subset of all available degrees of freedom is actually controlling the materials’ behavior of interest. Searching over a large dimensional space when only a small subspace is of interest may be highly computationally inefficient. A challenge is then how to discover the dominant degrees of freedom when very little data is available and no proper feature selection can be carried out at the outset of the discovery process. The problem may become more complex due to the existence of interaction effects among the covariates since such interactions are extremely challenging to discover when the available data is very sparse.

We note that there are some more flexible GP-based models, like automatic relevance detection (ARD),27 which introduces a different scale parameter for each input variable inside the covariance function to facilitate removal of unimportant variables and may alleviate the problem. Recently, Talapatra et al.14 proposed a robust model for f, based on Gaussian mixtures and Bayesian model averaging, as a strategy to deal with the data dimension and sparsity problem. Their framework was capable of detecting subspaces most correlated with optimization objectives by evaluating the Bayesian evidence of competing feature subsets. However, their covariance functions, and in general, most commonly used covariance functions for GP usually induce smoothness property and assume continuity for f, which may not necessarily be warranted and limit its performance when f is non-smooth or has sudden transitions—this may be a common occurrence in many MD challenges. Also, GP-based methods may still not perform well when the dimension of predictors is relatively high or the choice of the kernel is not suitable for the unknown function10,12. Apart from these solutions, there is a broad literature on flexible nonstationary covariance kernels28. Deep network kernel is a prominent recent example29 while its strength may be limited when faced with sparse datasets.

The focus of this paper is to replace GP-based machine learning models with other, potentially more adaptive and flexible, Bayesian models. More specifically, we explore Bayesian spline-based models and Bayesian ensemble-learning methods as surrogate models in a BO setting. Bayesian multivariate adaptive regression splines (BMARS)30,31 and Bayesian additive regression trees (BART)32 are used in this paper as they can potentially be superior alternatives to GP-based surrogates, particularly when the objective function, f, requires more flexible models. BMARS is a flexible nonparametric approach based on product spline basis functions. BART belongs to Bayesian ensemble-learning-based methods and fits unknown patterns through a sum of small trees. Both of them are well equipped with automatic feature selection techniques.

In this article, we present a fully automated experimental design framework that adopts BART and BMARS as the surrogate models used to predict the outcome(s) of yet-to-be-made observations/queries of/to the expensive “black-box” function. The surrogates are used to evaluate the acquisition policy within the context of BO. Automated algorithm-based experimental design is a growing technology used in many fields such as materials informatics, and biosystems design22,33,34. It combines the principles of specific domains with the use of machine learning to accelerate scientific discovery. We compare the performance of this BO approach using non-GP surrogate models against other GP-based BO methods using standard analytic functions, and then present results in which the framework has been applied to realistic materials science discovery problems. We then discuss the possible underlying reasons for the remarkable improvements in performance associated with using more flexible surrogate models, particularly when the (unknown) objective function is very complex and does not follow the underlying assumptions motivating the use of GPs as surrogates.

Results

Simulation studies

In this section, we present two simulation studies where we set the Rosenbrock35 and the Rastrigin36,37 functions as the black-box function(s) to optimize, respectively. Figure 1 shows a two-dimensional example for each of them. They are two commonly used test functions in optimization benchmark studies. In both optimization tasks, the goal is to find the global minimum point of the unknown function. Therefore, we record the minimum value of observed response y in each iteration for each model for comparison. As shown in Fig. 2, a faster decline of the curve indicates a more efficient search for the target point and better performance.

Fig. 1: Plots of black-box functions.
figure 1

a The valley of a two-dimensional Rosenbrock function which has the formula \({{{\bf{y}}}}=100{({{{{\bf{x}}}}}_{2}-{x}_{1}^{2})}^{2}+{({{{{\bf{x}}}}}_{1}-1)}^{2}\). b The frequent and regularly distributed local minima of a two-dimensional Rastrigin function which has the formula \({{{\bf{y}}}}=20+\mathop{\sum }\nolimits_{i = 1}^{2}[{{{{\bf{x}}}}}_{i}^{2}-10\cos (2\pi {{{{\bf{x}}}}}_{i})]\).

Full size image
Fig. 2: The average minimum y observed based on each model in each iteration.
figure 2

a Rosenbrock function with the initial set of sample size N = 10. b Rosenbrock function with the initial set of sample size N = 20. c Rastrigin function with the initial set of sample size N = 10. d Rastrigin function with the initial set of sample size N = 20.

Full size image

As for the probabilistic models, we compare our proposal, which uses BART32 and BMARS30, with the popularly used baseline GP regression with Radial-basis function (GP RBF) kernel38. At the same time, RBK kernel with ARD (GP RBK ARD)27 is considered, as well as nonstationary kernels like the dot-product kernel (GP Dot)39 and more flexible deep network kernel (GP DKNet)29. We also compare them with the Bayesian model average using GP (BMA1 and BMA2)14, which showed an edge over the benchmark method. BMA1 and BMA2 refer to the use of first- or second-order Laplace approximation to calculate the relevant marginal probabilities of the mixture model. We use a constant mean function for all the GP-based modes above. For the acquisition function, we choose the expected improvement (EI) metric3 for all the models. To ensure a fair comparison, we also use a random search within the inner optimization problem of the acquisition function.

In order to have a comprehensive performance evaluation, we begin the optimization of the above models with five different sizes of initial datasets (N = 2, 5, 10, 15, 20) that are uniformly sampled from the search space14. As for each N and each algorithm, the results are based on 100 replicates. To reduce the number of iterations, we choose two samples each time in the workflow. For the stopping criteria, it is regarded as running out of the budget which is set as 80 function evaluations. Relevant results for N = 10, 20 are depicted in Fig. 2 and those for other N values can be referred to in Supplementary Note 1.

The Rosenbrock function, also called the Valley or Banana function, is often used as a test case for optimization algorithms36,40. The formula of a d-dimensional Rosenbrock function is as follows:

$$f({{{\bf{x}}}})=\mathop{\sum }\limits_{i=1}^{d-1}[100{({{{{\bf{x}}}}}_{i+1}-{{{{\bf{x}}}}}_{i}^{2})}^{2}+{({{{{\bf{x}}}}}_{i}-1)}^{2}].$$
(1)

This function is unimodal, with the global minimum being at x* = (1, …, 1) with f(x*) = 0, which lays inside a long, narrow, parabolic-shaped flat valley as shown in Fig. 1a. In this function, we have a continuous search space and for each xi the range is [−2, 2]. During the workflow, locating the valley is trivial. However, further convergence to the global optimum is difficult, making this a good test problem.

Here, we set d = 4 and simulate the data. Apart from these four important predictors, we also add four uninformative predictors that follow the standard normal distribution. These four new-added features do not affect the response but are designed to augment the dimensionality of the problem, potentially obfuscating the solution and “frustrating” the optimizers. This enables us to check whether these frameworks can reveal true factors properly and lead to an efficient exploration. Otherwise, a lot of unnecessary searches occurring among the insignificant directions can slow down the process of locating the optimum point. Moreover, the quality of the predictions may suffer as a result.

As seen in Fig. 2a, b, the solid blue curves for BMARS show the sharpest decrease, suggesting that it is the most efficient optimizer. BART-based BO (solid red curve) also exhibits competitive performance, relative to popular GP-based techniques like GP (RBK ARD) (solid gray curve), BMA1 (solid dark green curve), and BMA2 (dotted orange curve). Meanwhile, GP (DKNet) (dotted purple curve) cannot show its strength and drops slowly as it requires considerably more data to be trained properly. As seen from (1), the Rosenbrock function overall is a polynomial function with a good smoothness property, which may explain why GP-based surrogates perform competitively despite not being the best. Turning to the final stable stage, it is the blue curve (BMARS) that firstly shows a flat pattern and is closest to the optimum value f(x*) = 0.

Turning to the Rastrigin function36,40, it is a nonconvex function used to measure the performance of optimization workflows. The formula for a d-dimensional Rastrigin function reads as follows:

$$f({{{\bf{x}}}})=10d+\mathop{\sum }\limits_{i=1}^{d}[{{{{\bf{x}}}}}_{i}^{2}-10\cos (2\pi {{{{\bf{x}}}}}_{i})].$$
(2)

It is based on a quadratic function with an addition of cosine modulation which brings about frequent and regularly distributed local minima as depicted in Fig. 1b. Similar to Rosenbrock’s case, the search space is continuous and we focus on [−2, 2] for each direction. Thus, the test function is highly multimodal, making it a challenging task where algorithms easily get stuck in local minima. The global minimum point is x* = (0, …, 0) and f(x*) = 0.

For the simulated data, we set d = 10 and again we add five uninformative features following a standard normal distribution. With these five additional variables (or design degrees of freedom), we can assess whether these frameworks are capable of detecting the factors that are truly correlated with the objective function, enabling an efficient exploration of the design space.

As seen in Fig. 2c, d, the solid blue curves for BMARS again exhibit the fastest decline, indicating the best performance. The BART-based BO (solid red curves) follows and presents similar decreased speed with most of the GP-based methods. However, the dotted brown curve seems to be the slowest, which is for the baseline GP (RBK). Considering the convergent stage, the blue curve reaches it between 50 and 60 iterations and the minimum observed y is very close to the global optimum value f(x*) = 0. The other methods remain in a decreasing pattern with larger values of the minimum observed y. It is no surprise that GP-based methods suffer under this scenario, for which Rastrigin function’s quick switch between different local minima may be the reason, especially for GP (RBK). In contrast, with the flexible bases constructed and multiple tree models, BMARS and BART are able to capture this complex trend of f. We note that BART might need a few more training samples to gain more competitive advantages over more flexible GPs like BMA1 and BMA2 due to block patterns of Rastrigin function.

Having established the better overall performance of our proposed non-GP base functions applied to complex BO problems, we will now turn our attention to two materials science-motivated problems.

MD in the MAX phase space

MAX phases (ternary layered carbides/nitrides)14,41 create an adequate system to investigate the behavior of autonomous materials design frameworks, as a result of both their chemical richness and the wide range of their properties. The pure ternary MAX phase composition palette has so far been explored to a limited degree, so there is also significant potential to reveal promising chemistries with optimal property sets14,42,43. For these reasons, we compared different algorithms for searching among the Mn + 1AXn phases, where M refers to a transition metal, A refers to group IV and VA elements, and X corresponds to carbon or nitrogen.

Specifically, the materials design space for this work consists of the conventional MAX phases M2AX and M3AX2, where M ∈ {Sc, Ti, V, Cr, Zr, Nb, Mo, Hf, Ti}, A ∈ {Al, Si, P, S, Ga, Ge, As, Cd, In, Sn, Tl, Pd}, and X ∈ {C, N}. The space is discrete which includes 403 stable MAX phases in total, aligned with Talapatra et al.14. More discussion about the discrete space in BO can be found in Supplementary Note 4. The goal of the automated algorithm is to provide a fast exploration of the material space, namely to find the most appropriate material design, which is either (i) the maximum bulk modulus K or (ii) the minimum shear modulus G. The results in the following sections are obtained with the aim (i), while those for (ii) can be found in Supplementary Note 2. We point out that while the material design space is small, knowledge of the ground truth can assist significantly in the verification of the solutions arrived at by different optimization algorithms.

For the predictors, we follow the setting in Talapatra et al.14 and consider 13 possible features in the model: empirical constants C, m, which link the elements of the material to its bulk modulus; valence electron concentration Cv; electron to atom ratio \(\frac{e}{a}\); lattice parameters a and c; atomic number Z; interatomic distance Idist; the groups corresponding to the periodic table of the M, A, and X elements ColM, ColA, ColX, respectively; the order O of MAX phase (whether of order 1 according to M2AX or order 2 according to M3AX2); and the atomic packing factor (APF). We note that the features above can potentially be correlated with the intrinsic mechanical properties of MAX phases, although a priori we assume that we have no knowledge as to how such features are correlated. In practice, as was found in ref. 14, only a small subset of the feature space is correlated with the target properties. We note that in ref. 14 the motivation for using Bayesian model averaging was precisely to be able to detect subsets within the larger feature set most effectively correlated with the target properties to optimize.

For the probabilistic model, we align with the simulation study above and compare our suggested framework that uses BART32 and BMARS30 to the widely used baselines, including GP (RBK)38, GP (RBK ARD)27, GP (Dot)39, Bayesian model average using GP (BMA1 and BMA2)14, and GP (DKNet)29. For the acquisition function, we choose EI for each of them to ensure a fair comparison. To get a comprehensive picture, we follow the structure in the previous section (where we studied the benchmark Rosenbrock and Rastrigin functions) and start the above models with five different sizes of initial samples (N = 2, 5, 10, 15, 20), which are randomly chosen from the design space. For each N, the results are based on 100 replicates. To avoid an excessive number of iterations, we add two materials at a time in the platform. For the stopping criteria, it is set as successfully locating the material with ideal properties or running out of the budget which is set as 80, roughly 20% of the available space. For these replicates not converging within the budget, we follow Talapatra et al.14 and regard their number of calculations as 100 to avoid an excessive number of evaluations.

Due to the high cost per experiment, the framework has better performance if it needs a fewer number of experiments before finding the candidate with desired properties. Therefore, we use it as a vital criterion for evaluating model capabilities. Table 1 shows the mean value and interquartile range (IQR) of the total number of evaluations searching for the maximum bulk modulus K within the MAX phase design space. The smaller values of the mean and IQR indicate a more efficient and stable platform.

Table 1 The mean value and interquartile range (IQR) of the number of experiments based on each model to find the maximum bulk modulus K in MAX phases with the initial set of sample size N ∈ {2, 5, 10, 15, 20}.
Full size table

As depicted in Table 1, while GP (Dot), BMA1, and BMA2 are more efficient than GP (RBK) and GP (DKNet) when looking for the maximum bulk modulus K, BART and BMARS can further greatly reduce the number of experiments and maintain a more stable performance compared to GP-based models. For GP (RBK ARD), it achieves good speed when N is larger than 10, but shows poor and unstable performance under small N. Also, considering the interquartile range of each model, BART and BMARS tend to be more robust under each setting and can achieve the goal before 80 iterations, while the other five are more likely to run out of the budget without achieving the objective.

Two possible reasons could explain why BMARS and BART can improve the searching speed much more efficiently than competing strategies. On the one hand, BMARS and BART are known to be more flexible surrogates compared to GP-based methods and are more powerful when faced with unknown and complex mechanisms in real-world data. On the other hand, BMARS and BART usually scale better with the dimension and can be more robust when handling high or even moderately dimensional design spaces.

In MD problems, beyond the identification of optimal regions in the materials design space, it is also desirable to understand the factors/features most correlated with the properties of interest. By taking these predictor and interaction rankings into account, researchers can gain a deeper understanding of the connection between features and material properties. We present the relevant results for the maximum bulk modulus K, and those for the minimum shear modulus G are in Supplementary Note 2. BART and BMARS are endowed with automatic feature selection based on their appearances in the corresponding surrogate models, while baselines GP (RBK) and GP (Dot) cannot identify feature importance relative to the BO objective. Although BMA1 and BMA2 can utilize the coefficient of each component to provide some information about feature importance, they cannot directly tell the exact order of individual variables and interactions.

Under five different scenarios N ∈ {2, 5, 10, 15, 20}, Tables 2 and 3 list the top 5 important factors aimed at the maximum value of K using BART and BMARS, respectively. The rankings are based on the median inclusion times of the 100 replicates from the last model when the workflow stops. When using BART, ColA, \(\frac{e}{a}\), ColM, APF, and Idist are the most useful. While turning to BMARS, ColA, \(\frac{e}{a}\), c, a, APF, and Idist always play a key role. We can see a similar pattern for the top-ranked features between the two models for different N, although some differences exist in their order. Regarding the interactions among features, we measure their importance by counting the coexistence of two of them within each basis function. The more frequently they are used in the same basic function, the greater their influences on material improvement are. The detailed results for the interaction selection can be referred in Supplementary Note 2.

Table 2 The top 5 important factors selected by BART for the maximum bulk modulus K in MAX phases with the initial set of sample size N ∈ {2, 5, 10, 15, 20}.
Full size table
Table 3 The top 5 important factors selected by BMARS for the maximum bulk modulus K in MAX phases with the initial set of sample size N ∈ {2, 5, 10, 15, 20}.
Full size table

During the material development process, we may not know which features we should add to the model in advance. In light of this, it is usually the case that one considers all possible features during the training and optimization to avoid missing important features. This brings an important challenge because it is often not possible to carry out any sort of feature selection ahead of the experimental campaign. Moreover, GP-based BO frameworks tend to become less efficient as the dimension of the design space increases as the required coverage to ensure adequate learning of the response surface is exponential with the number of features11. Moreover, the sparse nature of the sampling scheme—BO, after all, is used when there are stringent resource constraints to query the problem space—makes the (learned) response surface very flat over wide regions of the design space, with some interspersed, local highly nonconvex landscapes44. These issues make high-dimensional BO very hard. In materials science problems, a key challenge is that many of the potential dimensions of the problem space are uninformative, i.e., they are not correlated with the objective of interest.

It is thus desirable to develop frameworks that are robust against the existence of possibly many uninformative or redundant features. To further check the platform’s utility to distill useful information and maintain the speed, we simulate 16 random predictors following the standard normal distribution and mix them with the 13 predictors described above. With these new non-informative features, we use the same automated framework and explore the space for the materials with ideal properties.

As shown from Table 4, BART’s performance is not degraded by the newly added unhelpful information and is still the most efficient choice, indicating its robust property. At the same time, although BMARS is slower than the best, it is still competitive compared to other GP-based approaches like BMA1 and BMA2. BART-based BO is clearly capable of detecting non-informative features in a very effective manner.

Table 4 The mean value and interquartile range of the number of experiments based on each model to find the maximum bulk modulus K in MAX phases with additional non-informative features with the initial set of sample size N ∈ {2, 5, 10, 15, 20}.
Full size table

We also find the top 5 features as well as interaction effects for both BART and BMARS. For the 16 newly added unimportant features, we denote them by n1, …, n16. Tables 5 and 6 summarize the most significant features. We can see that the results do not include n1, …, n16, indicating a good ability to filter out useless information. Compared with Table 2, we can also notice that the outputs of BART are very similar to those without additional non-informative data and ColA, \(\frac{e}{a}\), ColM, APF, and Idist are again frequently chosen in different N showing a robust performance. While compared with Table 3, the selections from BMARS experience more changes and are more influenced by this uncorrelated knowledge.

Table 5 The top 5 important factors selected by BART for the maximum bulk modulus K in MAX phases with additional non-informative features with the initial set of sample size N ∈ {2, 5, 10, 15, 20}.
Full size table
Table 6 The top 5 important factors selected by BART for the maximum bulk modulus K in MAX phases with additional non-informative features with the initial set of sample size N ∈ {2, 5, 10, 15, 20} using BMARS.
Full size table

Moving to the interaction effects, BART successfully neglects unimportant features and maintains its performance. At the same time, BMARS is capable of (almost) filtering out all non-informative features and only leaves a small portion of the interactions between new predictors and the original data. Exact selection results can be found in Supplementary Note 2.

Optimal design for stacking fault energy in high entropy alloy spaces

To further demonstrate our model’s advantage, we search among a much larger discrete material design space whose size is 36,273 instead of 403 in the previous section. This dataset represents face-centred cubic (FCC) compositions in the 7-element CoCrFeMnNiV-Al high entropy alloy (HEA) space. Specifically, we focus on the task of exploring the stacking fault energy (SFE) chemical landscape in this system. SFE is an intrinsic property of crystals that measures their inherent resistance for adjacent crystal plans to shear against each other. Its value can be a good indicator of the (dominant) plastic deformation mechanism of the alloy and is thus a valuable alloy design parameter45,46. The SFE in this alloy system has been predicted for each composition using a support vector regressor trained on 498 high-fidelity SFE calculations from density functional theory (DFT) using the axial-next-nearest-neighbor-Ising model47,48 relating SFE to the lattice energies of (disordered) FCC, hexagonal close-packed (HCP) and double HCP (DHCP) crystals of the same chemical composition. In addition to SFE, stoichiometrically weighted averages and variances were calculated for each composition for 17 pure element properties to generate a total of 34 property-based features.

In this new analysis, we have two goals: namely, to find the global minimum and global maximum in the SFE landscape. Thus, we record the minimum value and the maximum value of the observed response in each iteration for each model for comparison. As we can see, a faster curve increase in Fig. 3a, b and a sharper curve decline in Fig. 3c, d indicate a more efficient search for the target point and better performance.

Fig. 3: The average maximum or minimum stacking fault energy (SFE) [mJ⋅m−2] observed on each model in each iteration.
figure 3

a The maximum SFE with the initial set of sample size N = 10. b The maximum SFE with the initial set of sample size N = 20. c The minimum SFE with the initial set of sample size N = 10. d The minimum SFE with the initial set of sample size N = 20.

Full size image

For the predictors, we choose 41 potential predictors (34 property-based features in addition to the compositions of the seven constituent elements), which provides a larger set of candidate features. This set is a mixture of informative and (potentially) uninformative features and some of the informative features are correlated to each other, which may bring about a more challenging feature selection task. We follow the analysis above and compare our suggested framework that uses BART32 and BMARS30 to the GP regression (RBK, RBK ARD, Dot, and DKNet)27,29,38,39 and Bayesian model average using GP (BMA1 and BMA2)14. For the acquisition function, we continue using EI for each of them to maintain a fair comparison. Also, we start the above models with five different sizes of initial samples (N = 2, 5, 10, 15, 20), which are randomly chosen from the design space. For each N, the results are based on 100 replicates. Curves for N = 10 and 20 are presented here and outputs under other initial sample sizes are summarized in Supplementary Note 3.

As seen in Fig. 3a, b, when looking for the maximum SFE, the solid blue curves for BMARS, solid red curves for BART, and dotted light blue curves for GP (Dot) have the sharpest increase, indicating the best performance. While the other curves representing other GP-based surrogates tend to move slowly. The figure shows that BART- and BMARS-based BO is capable of finding the materials with SFE values close to the ground-truth maximum in the dataset in ~80 iterations, corresponding to just 0.25% of the total materials design space that could be explored. This is an impressive performance that is eclipsed when considering the performance of BART/BMARS-BO in the minimization problem, as shown in Fig. 3c, d. In Fig. 3c, d, the blue curves for BMARS and red curves for BART drop much faster than other curves, which confirms a more efficient search ability of our methods. In this case, by about ~40 iterations, the optimizer has converged to the points extremely close to the ground-truth minimum in the dataset. This corresponds to about 0.125% of the total materials design space. In this case, the performance of the proposed frameworks is much better than most of the alternatives. Here we note that, although GP (Dot) performs better than BMARS or BART in a few settings, an additional advantage of the latter methods is the automatic detection of important features detailed below.

In this case study, not only the design space has become much larger but also the number of candidate design features has increased. Using other approaches, it would be more difficult to evaluate the significance of the different features (or degrees of freedom) as well as their interactions. Here, we present the corresponding results for finding the maximum SFE, and those for the minimum SFE are in Supplementary Note 3.

Under five different scenarios N ∈ {2, 5, 10, 15, 20}, Tables 7 and 8 list the top five factors most correlated with the maximum in the SFE using BART and BMARS, respectively. The rankings are based on the median inclusion times of the 100 replicates from the last model when the workflow stops. For BART, Specific.Heat_Avg, Pauling.EN_Var, Mn, and Ni are the most important features. Meanwhile, turning to BMARS, Specific.Heat_Avg, Pauling.EN_Va, C_11_Avg, and Mn always play vital roles. Comparing top-ranked features for sets of different N, we observe similar patterns, but with a few differences in order. Immediately, one can see that only a few chemical elements are detected to be strongly correlated to the SFE in this HEA system and that, instead, other (atomically averaged) intrinsic properties may be more informative when attempting to predict this important quantity. This implies that focusing exclusively on chemistry as opposed to derived features may not have been an optimal strategy towards BO-based exploration of this space. Notably, Ni figures as the feature highly correlated to SFE in almost all scenarios considered. This is not surprising as Ni is also highly correlated with the stability of FCC over competing phases (such as HCP), and thus, higher Ni content in an alloy should be correlated to higher stability of FCC and higher SFE49. Co and Mn also appear as important covariates. In the case of Co, limited experimental studies have shown that increased Co tends to result in lower SFEs in FCC-based HEAs50. While trying to understand the underlying reasons for why other covariates (Specific hear, Pauling Electronegativity, etc.) seem to be highly correlated to SFE is beyond the scope of this work, what is notable is that in this framework, such insights can be gleaned at the same time that the materials problem space is being explored. Thus, in an admittedly limited manner, the BART/BMARS-BO framework not only assists in the (very) efficient exploration of materials design spaces but also enhances our understanding of the underpinnings of material behavior. More results about the interactions among features are presented in Supplementary Note 3.

Table 7 The top five important factors selected by BART for the maximum stacking fault energy (SFE) with the initial set of sample size N ∈ {2, 5, 10, 15, 20}.
Full size table
Table 8 The top five important factors selected by BMARS for the maximum stacking fault energy (SFE) with the initial set of sample size N ∈ {2, 5, 10, 15, 20}.
Full size table

Discussion

In general, there are two major categories of BO: (i) acquisition-based BO (ABO), and (ii) partitioning-based BO (PBO). ABO10,12,36 is the most traditional and broadly used BO. The key idea is to pick an acquisition function, which is derived from the posterior and then optimized at each iteration to specify the next experiment. On the other hand, PBO36,51 successfully avoids the optimization of acquisition functions by intelligently partitioning the space based on observed experiments and exploring promising areas, greatly reducing computations. Compared to PBO, ABO usually makes better use of the available knowledge and makes higher quality decisions, leading to a fewer number of needed experiments. In this study, we focused on ABO to construct the autonomous workflow for material discovery.

GP-based BO has been widely used in a number of areas and gradually become a benchmark method12,13,24 for optimization of expensive “black-box” functions. However, its power can be limited by the intrinsic weaknesses of GP10,12. Isotropic covariance functions such as the Matérn and Gaussian kernels commonly employed in the literature have continuous sample paths, which is undesirable in many problems including material discovery as it is well known that the behavior of materials often changes abruptly with minute changes in chemical make-up or (multiscale) microstructural arrangements. Moreover, such isotropic kernels are provably suboptimal52 in function estimation when there are spurious covariates or anisotropic smoothness. While remedies have been proposed in the literature involving more flexible kernel functions with additional hyperparameters53 and sparse additive GPs54,55, tuning and computation of such models can be significantly challenging, especially given a modest amount of data. Thus, in complex material science problems such as ours, Bayesian approaches based on additive regression trees or multivariate splines constitute an attractive alternative to GPs. Attractive theoretical properties of BART, including adaptivity to the underlying anisotropy and roughness, have recently appeared56.

In this paper, we proposed a fully automated experimental design pipeline where we took advantage of more adaptive and flexible Bayesian models including BMARS30,31 and BART32 within an otherwise conventional BO procedure. A wide range of problems in scientific studies can be handled with this algorithm-based workflow, including MD. Both the simulation studies and real data analysis applied to scientifically relevant materials problems demonstrate that using BO with BMARS and BART outperforms GP-based methods in terms of searching speed for the optimal design and automatic feature importance determination. To be more specific, due to its well-designed spline basis, BMARS is able to catch challenging patterns like sudden transitions in the response surface. At the same time, BART also ensembles multiple individual trees and leads to a strong regression algorithm. Resulting from the recursive partitioning structures, they are equipped with a model-free variable selection that is based on feature inclusion frequencies in their basic functions and trees. This enables them to more accurately recognize the trends and correctly reveal the true factors.

We would like to close by briefly discussing potential applications of the framework in the context of autonomous materials research (AMR). Recently, the concept of autonomous experimentation for MD57 has quickly emerged as an active area of research58,59,60. Going beyond traditional high-throughput approaches to MD61,62,63, AMR aims to deploy robotic-assisted platforms capable of the automated exploration of complex materials spaces. Autonomy, in the context of AMR, can be achieved by developing systems capable of automatically selecting the experimental points to explore in a principled manner, with as little human intervention as possible. Our proposed non-GP BO methods seem to have robust performance against a wide range of problems. It is thus conceivable that the experimental design engines of AMR platforms could benefit from algorithms such as those proposed here.

Methods

Bayesian optimization

BO10 is a procedure intended to determine the global minimum (or maximum, with the similar procedure) x* of an unknown objective function f sequentially and optimally, where \({{{\mathcal{X}}}}\) denotes the search space:

$${{{{\bf{x}}}}}^{* }=\mathop{{\mathrm{argmin}}}\limits_{\{{{{\bf{x}}}}\in {{{\mathcal{X}}}}\}}f({{{\bf{x}}}}).$$
(3)

In the common setting of BO, the target function f can be either “black box” or expensive to evaluate, as such a function may represent a resource-intensive experiment or a very complex set of numerical simulations. Thus, we would like to reduce the number of function evaluations as we explore the design space and search for the optimal point. It mainly includes two steps: (i) fitting the hidden pattern of the target function, f, given observed data D so far based on some surrogate models, and (ii) optimizing selected utility or acquisition functions u(x∣D) based on the posterior distribution of the surrogate estimates of f in order to decide the next sample point to evaluate in the design space \({{{\mathcal{X}}}}\). To be more specific, it generally follows Algorithm 1:

Algorithm 1

Bayesian optimization (BO)

Input: initial observed dataset D = {(yi, xi), i = 1, …, N}

Output: candidate with desired properties

1: Begin with s = 1

2: while stopping criteria are not satisfied do (3 to 7)

3: Train the chosen probabilistic model based on data D

4: Calculate the selected acquisition function u(x∣D)

5: Choose the next experiment point by \({{{{\bf{x}}}}}^{s+1}={{{\mathrm{argmax}}}\,}_{\{{{{{\bf{x}}}}}^{s+1}\in {{{\mathcal{X}}}}\}}u({{{\bf{x}}}}| {{{\bf{D}}}})\)

6: Get the new point (ys + 1, xs + 1) and add it into the observed dataset D

7: s = s + 1

8: return the candidate with desired properties

A schematic illustration of BO is shown in Fig. 4—we note that such an algorithm can be implemented in autonomous experimental design platforms. Each of the subplots presents the state after one BO iteration, where they include the true unknown function (blue curve), utility function—in this case EI—(red curve), fitted values using GP (orange curve), 95% confidence interval (orange shaded area), observed samples (black points), and the next experiment recommended by the utility/acquisition function (gray triangle).

Fig. 4: Schematic illustration of Bayesian optimization (BO).
figure 4

Four subplots (a–d) give an example of the sequential automated experimental design using BO. They describe the true unknown function (blue curve), expected improvement (red curve), fitted values using GP (orange curve), 95% confidence interval (orange area), observed samples (black points), and the next experiment design (gray triangle) in each iteration.

Full size image

In this sequential optimization strategy, one of the key components is the Bayesian surrogate model for f, which is used to fit the available data34 and to predict the outcome—with a measure of uncertainty—of experiments yet to be carried out. Another important determinant of BO efficiency is the choice of the acquisition function34. It can assist in setting our expectations regarding how much we can learn and gain from a new candidate design. The next design structure to be tested is usually the one that maximizes the acquisition function, balancing the trade-off between exploration and exploitation of the design space. There are many commonly used acquisition functions, such as EI, probability of improvement, upper confidence bound, and Thompson sampling10,11. Here, we choose to use EI as the acquisition function, which can find the point that, in expectation, improves on \({f}_{n}^{* }\) the most:

$$u({{{\bf{x}}}})={{\mathbb{E}}{\mathbb{I}}}_{n}({{{\bf{x}}}}):={{\mathbb{E}}}_{n}[{(f({{{\bf{x}}}})-{f}_{n}^{* })}^{+}],$$
(4)

where \({f}_{n}^{* }\) is the maximum value observed so far, \({{\mathbb{E}}}_{n}[\cdot ]={\mathbb{E}}[\cdot | {{{{\bf{x}}}}}_{1:n},{{{{\bf{y}}}}}_{1:n}]\) is the expectation taken under the posterior distribution given the observed data, and \({b}^{+}=\max (b,0)\). We note that we have explored other acquisition functions and the relative performance of the corresponding methods with the same surrogates were not significantly different.

The choice of the surrogate model in BO will have a considerable impact on its performance, including the cost and time involved. As mentioned above, GPs64 have been widely applied in BO in many applications, including MD19. In this work, we utilize BMARS and Bayesian ensemble-learning models, in particular, BART, to help guide the search through the design space more efficiently. We will briefly introduce the potential surrogate models in BO. More detailed technical descriptions of them are included in Supplementary Methods.

GP and model mixing

One of the popular ways in BO is using GP regression as the surrogate model to approximate the unknown f. Given \({{{{\bf{x}}}}}_{i}\in {{\mathbb{R}}}^{p}\) (design feature vectors) and yi(i = 1, …, n) (evaluated f values at the corresponding xi’s, which can be noisy), we aim to fit the pattern of f and predict a new y* associated with x*. Usually, we assume that yi is a function of xi with additional noise: \({y}_{i}=f({{{{\bf{x}}}}}_{i})+{\epsilon }_{i},\ {\epsilon }_{i}\mathop{ \sim }\limits^{\,{{\mbox{i.i.d.}}}\,}{{{\mathcal{N}}}}(0,{\sigma }^{2})\). In GP regression, a GP prior is put on the unknown function f and \({{{\bf{f}}}}={(f({{{{\bf{x}}}}}_{1}),\ldots ,f({{{{\bf{x}}}}}_{n}))}^{\top }\) follows a joint Gaussian distribution:

$$p({{{\bf{f}}}}) \sim {{{\mathcal{N}}}}({{{\bf{f}}}}| m({{{\bf{x}}}}),{{{\bf{K}}}}),\quad [{K}_{ij}]=k({{{{\bf{x}}}}}_{i},{{{{\bf{x}}}}}_{j}),$$
(5)

where m(⋅) is the mean function and k(⋅, ⋅) is the kernel function.

A common choice for m(⋅) is a constant mean function. For k(⋅, ⋅), there are various candidates and we can decide it based on the corresponding task. The radial-basis function (RBF) kernel is popular to capture stationary and isotropic patterns. RBF kernels with ARD27 assign different scale parameters for each feature instead of using a common value27, which can help to identify key covariates determining f. There are also nonstationary kernels, such as dot-product kernels39 and more flexible deep network kernels29. For simplicity, we use D = {x1:n, y1:n} to denote the data we have collected. For a new input x*, the predictive distribution of response y* is:

$$p({y}_{* }| {{{{\bf{x}}}}}_{* },{{{\bf{D}}}})={{{\mathcal{N}}}}({\mu }_{* },{\sigma }_{* }^{2}),$$
(6)
$${\mu }_{* }=m({{{{\bf{x}}}}}_{* })+k({{{{\bf{x}}}}}_{* },{{{{\bf{x}}}}}_{1:n}){({{{\bf{K}}}}+{\sigma }^{2}{{{\bf{I}}}})}^{-1}({{{{\bf{y}}}}}_{1:n}-m({{{{\bf{x}}}}}_{1:n})),$$
(7)
$${\sigma }_{* }^{2}=k({{{{\bf{x}}}}}_{* },{{{{\bf{x}}}}}_{* })+{\sigma }^{2}-k({{{{\bf{x}}}}}_{* },{{{{\bf{x}}}}}_{1:n}){({{{\bf{K}}}}+{\sigma }^{2}{{{\bf{I}}}})}^{-1}k({{{{\bf{x}}}}}_{1:n},{{{{\bf{x}}}}}_{* }).$$
(8)

GP-based nonparametric regression approaches have gained a lot of popularity and have been widely used in various applications12,13,24. However, when turning to the sequential experiments in MD, the model may be imprecise and the search may be inefficient if we do not have enough information about the predictive performance of each experimental degree of freedom. Talapatra et al.14 address this issue by using model mixing to develop multiple GP regression models based on different combinations of the covariates and weigh all the potential models according to their likelihood of being the true model. In this way, they incorporated model uncertainty, leading to a more robust framework capable of adaptively discovering the subset of covariates most predictive of the objective function to optimize.

Bayesian multivariate adaptive regression splines

BMARS30,65 is a Bayesian version of the classical MARS model31, which is a flexible nonparametric regression technique. It uses product spline basis functions to model f and it automatically identifies the nonlinear interactions among covariates. The regression develops a relationship between the covariates \({{{{\bf{x}}}}}_{i}\in {{\mathbb{R}}}^{p}\) and the response yi(i = 1, …, n) as

$${y}_{i}=f({{{{\bf{x}}}}}_{i})+{\epsilon }_{i},\quad \hat{f}({{{{\bf{x}}}}}_{i})=\mathop{\sum }\limits_{j=1}^{l}{\alpha }_{j}{B}_{j}({{{{\bf{x}}}}}_{i}),\quad {\epsilon }_{i}\mathop{ \sim }\limits^{\,{{\mbox{i.i.d.}}}\,}{{{\mathcal{N}}}}(0,{\sigma }^{2}),$$
(9)

where αj denotes the relevant coefficient for the basic function Bj taking the form of

$${B}_{j}({{{{\bf{x}}}}}_{i})=\left\{\begin{array}{ll}1,&j=1,\\ \mathop{\prod }\limits_{q = 1}^{{Q}_{j}}{[{s}_{qj}\cdot ({{{{\bf{x}}}}}_{i,v(q,j)}-{t}_{qj})]}_{+},&j\in \{2,\,\ldots,\,l\},\end{array}\right.$$
(10)

with sqj ∈ {−1, 1}, v(q, j) denoting the index of the variables, and the set {v(q, j); q = 1, …, Qj} not repeated. Here tqj tells the partition location, \({(\cdot )}_{+}=\max (0,\cdot )\), and Qj is the polynomial degree of the basis Bj and also corresponds to the number of predictors involved in Bj. The number of parameters is O(l) and we set the maximum value of l as 500.

To obtain samples from the joint posterior distribution, the computation is mainly based on the reversible jump Metropolis–Hastings algorithms66. The sampling scheme only draws the important covariates, hence automatic feature selection is naturally done in this procedure.

Ensemble learning and BART

Apart from model mixing, ensemble learning67 provides an alternative way of combining models, which is a popular procedure that constructs multiple weak learners and aggregates them into a stronger learner68,69,70. In several circumstances, it is challenging for an individual model to capture the unknown complex mechanism connecting inputs to the output(s) by itself. Therefore, it is a better strategy to use a divide-and-conquer method in the ensemble-learning framework, which allows each of the models to fit a small part of the function. This is the key difference of our adopted Bayesian ensemble learning from the GP-based model mixing strategy in Talapatra et al.14. Ensemble learning’s robust performance to handle complex data makes it a great candidate for BO71. However, it has not been explored to its full potential in the context of optimal experimental design yet. Hence, we choose to combine BO with the Bayesian ensemble learning72, in particular, BART32. As BART is a tree-based model without inherent smoothness assumptions, it is also a more flexible surrogate model when modeling objective functions that are non-smooth, often encountered in MD. This strategy is effective and efficient due to its ability to take advantage of both the ensemble-learning procedure and the Bayesian paradigm.

BART32 is a nonparametric regression method utilizing the Bayesian ensemble-learning technique. Many simulations and real-world applications confirmed its flexible fitting capabilities73,74,75. Given \({{{{\bf{x}}}}}_{i}\in {{\mathbb{R}}}^{p}\) and yi(i = 1, …, n), where it approximates the target function f by aggregating a set of regression trees:

$${y}_{i}=f({{{{\bf{x}}}}}_{i})+{\epsilon }_{i},\quad \hat{f}({{{{\bf{x}}}}}_{i})=\mathop{\sum }\limits_{j=1}^{l}{g}_{j}({{{{\bf{x}}}}}_{i};{T}_{j},{{{{\boldsymbol{M}}}}}_{j}),\quad {\epsilon }_{i}\mathop{ \sim }\limits^{\,{{\mbox{i.i.d.}}}\,}{{{\mathcal{N}}}}(0,{\sigma }^{2}),$$
(11)

where Tj denotes a binary regression tree, \({{{{\boldsymbol{M}}}}}_{j}={({\mu }_{j1},\,\ldots,\,{\mu }_{j{b}_{j}})}^{\top }\) denotes a vector of means corresponding to the bj leaf nodes of Tj, and gj(xi; Tj, Mj) is the function that assigns μjt ∈ Mj to xi.

Using regularization priors on those trees is critical for the superior performance of this ensemble regression model. That way, each tree will be regularized to explain a small and distinct part of f. This aligns with the essence of ensemble learning, which is about combining weak learners into a stronger model. The number of parameters is correlated with the number of trees l as well as the tree depth dj and is O(l ⋅ 2d). In our analysis, l is set as 50 and dj is usually smaller than 6.

At the same time, one can use this regression model for automatic variable selection, which greatly expands its scope of use. The importance of each predictor is based on the average variable inclusion frequency in all splitting rules32. Bleich et al.76 further put forward a permutation-based inferential approach, which is a good alternative for the factor significance determination.

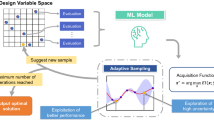
Automated experimental design framework

With BO using BMARS or BART, we propose an autonomous platform for efficient experimental design, aiming at significantly reducing the number of required trials and the total expense to find the best candidate in MD. The framework is depicted in Fig. 5 and the detailed description is as follows.

Fig. 5: Workflow of the automated experimental design framework.
figure 5

The overall workflow of the automated experimental design framework is based on Bayesian optimization with adaptive Bayesian learning.

Full size image

In this workflow, we begin with an initially observed dataset and the sample size can be as small as two. Then, we train our surrogate Bayesian learning model on the observed dataset and collect the relevant posterior samples. Using these samples, the acquisition function for each potential experiment to perform is calculated. After obtaining the values of the acquisition function, we select the candidates with top scores and do experiments at these points. With the new outcomes, the observed dataset is augmented and the stopping criteria are checked. If the criteria are fulfilled, we stop the workflow and return the candidate with the desired properties. Otherwise, we update the surrogate model by making use of the augmented dataset and use the updated belief to guide the next round of experiments.

Within this fully automated framework, what we need to provide is the initial sample and the stopping criteria. The beginning dataset can be some available data before this project. If we do not have this kind of information, we can randomly conduct a small number of experiments to populate the database and initialize the surrogate models used in the sequential experimental protocol. For the stopping criteria, it can be arriving at the desired properties or running out of the experimental budget14.