Ambipolar device simulation based on the drift-diffusion model in ion-gated transition metal dichalcogenide transistors

Abstract

Ionic gating is known as a powerful tool for investigation of electronic functionalities stemming from low voltage transistor operation to gate-induced electronic phase control including superconductivity. Two-dimensional (2D) material is one of the archetypal channel materials which exhibit a variety of gate-induced phenomena. Nevertheless, the device simulations on such ion-gated transistor devices have never been reported, despite its importance for the future design of device structures. In this paper, we developed a drift-diffusion (DD) model on a 2D material, WSe₂ monolayer, attached with an ionic liquid, and succeeded in simulating the transport properties, potential profile, carrier density distributions in the transistor configuration. In particular, the simulation explains the ambipolar behavior with the gate voltage comparable to the band gap energy, as well as the formation of p-n junctions in the channel reported in several experimental papers. Such peculiar behavior becomes possible by the dramatic change of the potential profiles at the Schottky barrier by the ionic gating. The present result indicates that the DD model coupled to the Poisson equation is a fascinating platform to explain and predict further functionalities of ion-gated transistors through including the spin, valley, and optical degrees of freedom.

Introduction

In ion-gated transistors, the electric double layer works as a gate dielectric layer of about 1 nm in thickness, and thus such transistors are called electric double layer transistors (EDLTs) or electrolyte gated transistors. Owing to its strong gate coupling, the operation voltage of EDLTs is dramatically reduced, and also, EDLT enables us to control the electronic phases including superconductivity¹. Materials for EDLTs are extremely rich including carbon nanotubes^2,3, organic semiconductors⁴, oxide materials⁵, two-dimensional (2D) materials such as graphene^6,7 and transition metal dichalcogenides (TMDs)^{8,9,10,11,12,13,14,15}.

In particular, TMDs have gained interest thanks to the intriguing phenomena coupled the valley and spin degrees of freedom. Thus, TMDs can be applied to electronic and spintronic applications^16,17. The TMD transistors are good candidates for the next-generation transistors since TMD semiconductors have enough band gap to switch ON/OFF states and high electron-hole mobilities^16,18. Moreover, the short channel effect is suppressed compared to the Si devices since the 2D structure allows easier gate control¹⁹. The characteristics of the conventional metal-oxide-semiconductor field-effect transistors (MOSFETs) are discussed mainly on MoS₂^{18,19,20,21,22,23,24}, WSe₂^{25,26,27,28,29,30}, and MoTe₂^31,32,33,34.

Ionic gating assists in realizing phenomena which are difficult to achieve in the conventional MOSFETs. The ambipolar behavior is one of those observed in ion-gated TMDs. In particular, hole transport in nominally n-type MoS₂ is observed only in EDLTs²⁴. This ambipolar nature allows us to fabricate lateral p–n junctions in the channel without chemical doping and asymmetric metal electrodes¹¹. By applying the source-drain bias voltage higher than the gate bias, the ionic distribution changes, allowing the ambipolar operation. Such ambipolar operation can be achieved also in the conventional transistors^25,35,36,37, but the operation voltage is significantly lower than that of the conventional FETs, and is in the voltage range similar to the bandgap energy. This offers an opportunity to determine the band gap directly from the transistor characteristics³⁸. It is also known that the p-n junctions formed in the channel emits circularly polarized light, and furthermore, the circular polarization can be flipped by changing the direction of the injected current¹³. This enables the generation of the circularly polarized light using the electric field. This circular dichroism is ascribed to the imbalance of K and K′ points in the band structure caused by the voltage^39,40. Moreover, the strong electric field induced by the ionic gating yields superconductivity in TMDs due to the high accumulation of carrier¹.

To achieve more benefit of the ionic gating, the device operation mechanism of EDLTs should be understood. For theoretical studies of transistor operations, the drift-diffusion (DD) method is known as a powerful tool for device simulation to calculate the transport properties, band profile, and spatial distribution of carriers inside devices. As the down-scaling is employed to realize high performance in conventional transistors, the DD simulation is used to design ideal device structures⁴¹. However, there has been no DD simulation reported on the ion-gated transistors of TMDs.

In this work, we developed a 2D layer transistor model including an ionic liquid (IL) as a gate dielectric, based on the DD method and succeeded in simulating the distribution of ions, and the dynamics of electron and holes passing through the metal contacts. We examined the characteristics of ion-gated TMD transistors whose device size is about submicron while the several micron is the common channel size reported in experiments. The simulation shows that the down-scaled ion-gated WSe₂ transistor holds ambipolar behavior and the formation of the p–n junctions reported in larger-scale devices^13,15,38. We clarified the transport mechanism and the fundamental physics underneath the transistor operation using the band profile and the spatial distribution of ions and carriers obtained by the calculation.

The mechanism of the ambipolar transistor has been discussed theoretically on organic and amorphous materials because it is easy to inject both electrons and holes due to the in-gap states^42,43. In single crystalline TMDs, such mid-gap states are absent. On the other hand, previous simulations on ion-gated organic transistors used a fixed capacitance induced by the ionic liquids^44,45, which cannot include the variation of the capacitance due to the modification of the ion distribution by the source-drain bias voltage and the back action from the carriers in semiconductors. The general perspective of the ambipolar transport in MOSFETs has been discussed in ref. ⁴⁶.

Some specific implementations are required to adopt the DD model to the ion-gated transistors. We explain the points which differ from the DD model used for the conventional transistors in the next section. After describing the model, we show the results of device simulations on the ion-gated WSe₂ transistors. The current, band profile and ion/carrier density distributions are examined for the unipolar and ambipolar operation.

Results and discussion

Drift-diffusion model for ion-gated transition metal dichalcogenide transistors

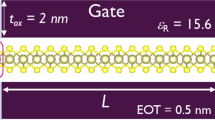
We start with the explanation of the DD model. We consider the 2D layer in (x, y) plane where the transport direction of the channel is set to x. The IL and oxide layer are piled up in the z direction as depicted in Fig. 1. We solve the continuity equation of each currents,

$$\frac{1}{q}\nabla {J}_{{\rm{n}}}(x)-R(x)=0,$$

(1)

$$-\frac{1}{q}\nabla {J}_{{\rm{p}}}(x)-R(x)=0.$$

(2)

Here, the electron and hole current densities are determined by well-known 1D Drift-Diffusion equations;

$${J}_{{\rm{n}}}(x)=-q{\mu }_{{\rm{n}}}n(x)\nabla \Phi (x,0)+q{D}_{{\rm{n}}}(x)\nabla n(x),$$

(3)

$${J}_{{\rm{p}}}(x)=-q{\mu }_{{\rm{p}}}p(x)\nabla \Phi (x,0)-q{D}_{{\rm{p}}}(x)\nabla p(x),$$

(4)

where J_n(p) denotes the electron (hole) current densities. q is elementary charge, n(x) [p(x)] is the electron [hole] density at location (x, 0) in WSe₂. n(x) and p(x) are defined in units of cm⁻². μ_n(p) is the mobility of the electron (hole) and D_n(p)(x) is the diffusion coefficient. Φ(x, 0) is the potential at position x. R(x) denotes the recombination rate, R(x) = R_dir(x) + R_SRH(x) + R_n(p)−con(x). We consider two types of the recombination rate; the direct recombination rate, R_dir(x), and the Shockley-Read-Hall (SRH) recombination rate, R_SRH(x), where

$${R}_{{\rm{dir}}}(x)=\beta [n(x)p(x)-{n}_{{\rm{in}}}^{2}],$$

(5)

and

$${R}_{{\rm{SRH}}}(x)=\frac{n(x)p(x)}{\tau [n(x)+p(x)]}.$$

(6)

Here, β is the direct recombination parameter and τ is the recombination time of the SRH recombination. n_in is the intrinsic carrier density of electrons and holes. For WSe₂, ${n}_{{\rm{in}}}=2{k}_{{\rm{B}}}T\frac{\sqrt{{{\rm{m}}}_{{\rm{e}}}{{\rm{m}}}_{{\rm{h}}}{{\rm{m}}}_{0}^{2}}}{\pi {\hslash }^{2}}\exp [-\frac{{E}_{{\rm{g}}}}{2{k}_{{\rm{B}}}T}] \sim 3\times 1{0}^{-6}$ cm⁻² at T = 220 K, where m_e(h) is the effective mass of electrons (holes), m₀ is the mass of free electrons, and k_B is the Boltzmann constant. R_n(p)−con(x) indicates the generation or annihilation rate of the carriers which enter or exit from the channel at x through the thermionic or tunnel current. Thus, the boundary conditions for n(x) and p(x) are determined by the continuity equation in Eqs. (1), (2). The detailed description of R_n(p)−con(x) is written in the Methods section.

Fig. 1: The schematic model of the ion-gated WSe₂ transistor.

The length of the structure in y direction is set to L_y = 100 nm.

We also solve the Poisson equation in the (x, z) plane in the whole system (WSe₂, ILs, SiO₂, and the metal contact)

$$\nabla {{\boldsymbol{\epsilon }}}_{\alpha }{\epsilon }_{0}\cdot \nabla \Phi (x,z)=-qC(x,z),$$

(7)

where C(x, z) = i⁺(x, z) − i⁻(x, z) for z > 0, C(x, z) = [p(x) − n(x)]/d for −d < z < 0, and C(x, z) = 0 for z < −d. Here, i⁺(x, z) and i⁻(x, z) are cation and anion concentrations, respectively (see Methods section for detail). d is the thickness of the WSe₂ layer, ϵ_α is the relative permittivity of the material α (α ∈ WSe₂, SiO₂, and IL), and ϵ₀ is the permittivity of vacuum. ${{\boldsymbol{\epsilon }}}_{{{\rm{WSe}}}_{2}}$ is direction dependent as shown in Table 1. The boundary condition is set to satisfy the continuity of the normal vector of the electric flux density at the interface between materials. The boundary condition at the metal contact is set as Φ(x, t_IL) = V_gs + Φ(x_s, 0), where t_IL is the thickness of IL. At the other edges, we adopt the Neumann’s boundary condition, $\frac{\partial \Phi (0,z)}{\partial x}=\frac{\partial \Phi ({L}_{x},z)}{\partial x}=\frac{\partial \Phi (x,-{t}_{{{\rm{SiO}}}_{2}}-d)}{\partial z}=0$, where L_x is the length of WSe₂ layer in x direction, and ${t}_{{{\rm{SiO}}}_{2}}$ is the thickness of the SiO₂. The carrier densities [n(x) and p(x)] in the DD equation and the potential [Φ(x, z)] in the Poisson equation are determined self-consistently in the numerical calculations.

Table 1 Parameters used for WSe₂ and ions.

To adopt the above DD model to the ion-gated transistors, there are three points to be noticed regarding the difference between the conventional and ion-gated transistors. Firstly, in Eqs. (3) and (4) the ordinary Einstein relation between the mobility and the diffusion coefficient is not appropriate for ion-gated transistors since the ions attract the high concentration of carriers above 10¹³ cm⁻² while the carrier concentration is usually below 10¹² cm⁻² in the conventional transistors. Instead, we introduce the generalized Einstein relation (as explained in the Methods section) for the DD model at high carrier concentrations⁴⁷.

The second point is the treatment of the contact. It is known that metal-TMD junctions usually show the Schottky behavior in the conventional TMD transistors^48,49,50 with some exceptions such as ones using graphene or Scandium contacts^20,51. The mechanism of the Schottky transport has been precisely studied theoretically⁵². The conventional TMD transistors also have the problem of the Fermi-level-pinning due to the defect at the TMD-metal junctions⁵⁰. Thus, only n-type operations have been reported in many works for conventional MoS₂ FETs. However, the Fermi-level pinning seems to be weak in the ion-gated TMDs, according to the experimental results^13,30. We assume the contact made of an alloy of Ti and Au attached to semiconductor TMDs such as MoS₂ and WSe₂ acts as the n-type Schottky contact which only injects electrons. However, under the IL, as reported in ref. ¹³, the carrier of unipolar transport changes from electrons to holes by changing the sign of the gate voltage for small source–drain voltage. Furthermore, the electron current shows the linear increase by applying the source–drain voltage, which indicates the Ohmic contact. Thus, the boundary condition for the Schottky contact is not appropriate for the DD model. Moreover, the boundary condition for the Ohmic contact which can inject either electron and hole is also not appropriate. To realize both Ohmic and ambipolar behavior, we adopt a practical Schottky contact model, which realizes not only the Schottky contact but also the Ohmic contact for both electron and hole carriers⁵³. We expand the model in ref. ⁵³ from 3D structure to the 2D structure that can be applied to thin layer devices.

Thirdly, since the ion has the finite size, there is a limitation of ions per volume in the liquid. Note that the potential becomes too sharp around the interface compared to the real ionic potential if we consider the infinitesimal size of ions. The finite size of ions results in the screening between ions that affect the potential. We adopt the model including the screening effect of IL which can be applied beyond the classical Gouy-Chapman-Stern model⁵⁴. Note that the model is not applicable to the crowding situation of ions which occurs in the high gate bias voltage⁵⁵. We explain the concrete description of the model in the Methods section.

Device simulation of WSe₂ transistors

The schematic view of ion-gated monolayer WSe₂ transistors considered is depicted in Fig. 1. The employed parameters for the calculation are written in Table 1. The length of WSe₂ in the x (channel) direction is set at 100 nm and the source and drain contacts with 10 nm length are attached to the top of WSe₂ monolayer. We assume that electrons tunnel between metal contacts and the channel at x = 10 nm and x = 90 nm so that the real channel length is 80 nm. We set the energy difference between the work function of TMD and metal contact to 0.6 eV considering the metal contact made of the alloy of Ti and Au⁵⁶. In this calculation, we set the Fermi energy of the metal source contact to be zero. The energy level of the bottom of the conduction band is 0.6 eV at the source contact surface while the top of the valence band is −1.0 eV. The thickness of the IL is 10 nm and the metallic gate contact is attached to the top of the IL. The thickness of the SiO₂ layer at the bottom of the WSe₂ is 10 nm with the Neumann condition. We assume ions such as DEME-TFSI (N,N-diethyl-N-methyl-N- (2-methoxyethyl) ammonium bis (trifluoromethylsulfonyl)-imide) whose size is approximately 1 nm so that we fix the maximum ion concentration on the ion layer at the electric double layer to ${n}_{\max }=1\times 1{0}^{21}$ cm⁻³. The average ionic concentration is set to n_i = 2 × 10²⁰ cm⁻³. Though the employed n_i is lower than the real concentration due to the restriction in the numerical calculation (abrupt change of the carrier and ion concentrations), the approximate maximum of the IL capacitance is 40 μF/cm², which is large enough to bend the potential and make the Schottky barrier sufficiently thin so that the source and drain contacts show the Ohmic behavior. We use the constant mobility extracted from the experiment in ref. ¹⁵. We neglect the V_ds dependence of mobility since the potential is relatively flat inside the channel region beside the metal-TMD surface, as described later in the next section. Furthermore, we assume that the concentration of defects inside WSe₂ is negligible so that mobility is not affected by carrier concentration tuned by the gate voltage.

We start from examining the transport characteristics of ion-gated WSe₂ transistors using the theoretical model. As shown in Fig. 2a, b, the drain-source current, I_ds, is calculated as a function of the voltage determined from the potential difference between the source contact and the center of the ionic liquid, V_ref = Φ(10, 5 nm) − Φ(10 nm, 0) [see inset of Fig. 2b]. We should mention that V_ref is adopted in Fig. 2a, b instead of the gate voltage between the source contact and the metal gate, V_gs, to subtract the potential drop occurs at the surface of the gate contact for the considered system. Note that IL can be considered as two capacitors in series; one is the electric double layer capacitor (EDLC) of the gate electrode and the ionic liquid, and the other is the EDLC of WSe₂ and the ionic liquid. The surface area of the metal gate attached to the IL is usually much more substantial in experiments. Since the number of net ions at both capacitors should be the same, the ion concentration at the substantial metal gate is much smaller than the one at the WSe₂ surface. Thus, potential drops at the metal gate is negligible. However, in our calculation we set the surface area of the metal gate 100(nm)/80(nm) larger than the one of the WSe₂ due to the constraints of the numerical calculation. Thus, approximately half of the potential drops at the metal gate. So we define V_ref to compare the results with experiments. The bias voltage between the drain and source electrodes is set at V_ds = 0.2 V. Note that the current flows from the drain contact to the source contact when V_ds is positive. The center of the off-gate voltage slides to the minus (~ −0.2 V) from the zero point since the energy difference between the metal contact and WSe₂ is Φ_SB = 0.6 V which is 0.2 V above the center of the band gap. As shown in Fig. 2b, using the linear-scale plot, we estimate the threshold voltage from the intersection point of the line I_ds = 0 and the dotted linear line of the current. Here, the dotted line is determined from the least-square method using the data from 1.2 V < V_ref <1.5 V for the electron current, and −1.5 V < V_ref < −1.3 V for the hole current. The determined threshold voltage is V_th−e = 0.94 V for the electron current, and V_th−h = −1.17 V for the hole current, respectively. The threshold voltages for electrons and holes have been used to measure the bandgap of the semiconductor as reported in ref. ³⁸. In our numerical calculation, the energy difference between the threshold voltages of electron and hole currents is e(V_th−e − V_th−h) = 2.11 eV, which is 0.51 eV larger than the real band gap, E_g.

Fig. 2: Current and carrier concentration in the ion-gated WSe2 transistor.

a The log-scale plot of the current I_ds as a function of V_ref in the ionic-gated WSe₂ transistor. See Table 1 for the other parameters. b The linear-scale plot of the electron (blue) and hole (red) current as a function of V_ref. The right vertical axis is set for the electron current and the left vertical axis is set for the hole current. The dotted linear lines are determined by the least-square method using data from 1.3 V < V_ref <1.5 V for the electron current and −1.5 V < V_ref < −1.3 V for the hole current. The interaction points of I_ds= 0 and the linear lines indicate the threshold voltages for the electron and hole currents; V_th−e = 0.94 V, and V_th−h = −1.17 V respectively. c Net carrier concentration for V_ref = −2 V (V_ref ~ −1.46 V) [dot-dashed line], V_gs = 0.2 V (V_ref ~ 0.19 V) [solid line], and V_gs = 2 V (V_ref ~ 1.38 V) [dotted line].

Figure 2c shows the distribution of the net carrier concentration inside the channel. The current carrier is only electrons when V_ref > 0, while holes become carriers for V_ref < 0. Note that minor carrier is negligibly small and can not be determined by the numerical calculation. The carrier density of electrons or holes is almost constant besides the region around the contact.

Top panels in Fig. 3 show two-dimensional plots of the net ion density i⁺(x, z) − i⁻(x, z) for V_gs = −2 V (a: V_ref ~ −1.46 V), V_gs = 0.2 V (b: V_ref ~ 0.19 V), and V_gs = 2 V (c: V_ref ~ 1.38 V). At the interface attached to WSe₂, anions are dominant for V_ref < 0 while cations are dominant for V_ref > 0. The band profile of WSe₂ coupled to the metal contact is depicted in the bottom panels of Fig. 3. At V_gs = −2 V, the band bending is extremely sharp at the contact, and both bottom of the conduction band and top of the valence band are shifted above the quasi-Fermi energy, φ_n(p), in the channel. Around the contact-channel junctions, the potential bends downward which induces the Schottky barrier. The IL makes the thickness of the Schottky barrier of the valence band at Fermi level about 0.9 nm for the holes to tunnel through. Note that the quasi-Fermi energy is plotted only for the main carrier since the minor carrier is almost zero due to the rapid reduction of the carrier inside the band gap for WSe₂. At V_gs = 0.2 V, the quasi-Fermi level is located inside the band gap. Thus, the tunnel of the carrier between the contact and channel is prohibited. Only the Schottky (thermionic) transport is possible, but the simulation shows that it is negligible at this gate voltage. At V_gs = 2 V, the potential energy of the channel area becomes downward convex. Thus the quasi-Fermi energy is located at the conduction band which results in electron current. The carrier-type switching is possible with much smaller V_gs compared to the case in the conventional transistors. The ions play a role of dopant (surface doping) and induce the n-type contact by making the Schottky barrier of the conduction band at the Fermi level about 0.4 nm so that carriers can tunnel through. The Ohmic behavior is confirmed by the I_d-V_ds characteristics discussed below. Here, we show that both n-type and p-type operation are possible depending on the direction of the Schottky barrier controlled by the metal gate attached to the IL even if the work function of the metal contact is located at the upper part of the band gap as we set in this simulation.

Fig. 3: Ion density and band profile as a function of V_gs.

(Top) Net ion density i⁺(x, z) − i⁻(x, z) on the ionic liquid for a V_gs = −2 V (V_ref ~ −1.46 V), b V_ref = 0.2 V (V_ref ~ 0.19 V), and c V_gs = 2 V (V_ref ~ 1.38 V). The drain-source voltage is fixed to V_ds = 0.2 V. (Bottom) Band profile of WSe₂ and the metal. The dotted lines indicate the bottom of the conduction band, E_c (blue), and the top of the valence band, E_v (red). The solid lines denote the quasi-Fermi energy. See Table 1 for the other parameters.

Next, we calculate the I_d-V_ds characteristics at V_gs = 1.5 V where the carrier type is n-type. We plot the electron (dotted line), hole current (dot-dashed line), and the total current (solid line) as shown in Fig. 4. The I_ds-V_ds characteristics can be classified to the three regions: the linear (0 ⪅ V_ds ⪅ 1.2 V), the saturation (1.2 V ⪅ V_ds ⪅ 2.8 V), and the ambipolar region (V_ds ⪆ 2.8V). In the linear region, the current increases with V_ds approximately linearly around V_ds = 0 V, followed by the saturation region starting at V_ds ~ 1.2 V. Above V_ds ~ 2.8 V, I_ds takes off again, indicating the onset of hole current injected from the drain electrode (ambipolar transport). This feature is similar to the experimental output curve of WSe₂ device for larger devices¹³. The increase of electron current in the ambipolar region is due to the recombination of electrons and holes inside the channel.

Fig. 4: Drain current I_ds as a function of V_ds for the WSe₂ transistor.

The gate voltage is fixed to V_gs = 1.5 V. The lines indicate electron (dotted line), hole (dot-dashed line), and total current (solid line). See Table 1 for other parameters.

Figure 5 shows the 2D plot of the net ion density of the IL (top), and band profile of the WSe₂ channel and the metal contacts (bottom) for the linear region (a: V_ds = 0.5 V), saturation region (b: V_ds = 2.5 V) and ambipolar region (c: V_ds = 4 V). The figures from d to f are the enlarged views of the potential profile around the contacts. The open arrows denote the tunnel transport while the solid arrows denote the thermionic transport where carriers go beyond the barriers.

Fig. 5: Ion density and band profile as a function of V_ds.

a–c (Top) Net ion density i⁺(x, z) − i⁻(x, z) on the ionic liquid for a V_ds = 0.5 V, b V_ds = 2.5 V, and c V_ds = 4 V. The gate voltage is fixed to V_gs = 1.5 V. (Bottom) Band profile of WSe₂ and the metal. The Fermi-energy of the source contact is set to φ_metal = 0. The dotted lines indicate the bottom of the conduction band, E_c (blue), and top of the valence band, E_v (red). The solid lines are the quasi-Fermi energy for electron φ_n(x) (blue) and hole φ_p(x) (red). d–f The extension view of the potential profile around the contacts (x = 7–13 nm and x = 87–93 nm) for d V_ds = 0.5 V, e V_ds = 2.5 V, and f V_ds = 4 V. Black lines are the Fermi-level at the metal contacts. The arrows shows the transport direction of electrons (blue) and holes (red). The open arrows indicate the tunnel transport and the solid arrows denote the thermionic transport. The thicker arrows indicate the dominant paths of the current.

In the linear region (Fig. 5a), the cations are dominant at the interface attached to WSe₂. Therefore, the current is dominated by electrons since the band gap allows only electrons to tunnel through the metal-WSe₂ junctions as depicted in Fig. 5d. By increasing the bias voltage V_ds, the electrons tunneling from the channel to the drain contact gains. The inclination of the current in the linear region is estimated to be 7.5 × 10⁻⁵ Ω⁻¹. Thus, the estimated contact resistance is R_con ~ 10 kΩ while the channel resistance is R_ch = 1∕qμ_nn ~ 4 kΩ (n ~ 4 × 10¹³ cm⁻² as discussed below) so that the contact resistance is comparable to the channel resistance, which results in the linear behavior.

In the saturation region, cations are dominant at the interface attached to WSe₂ while anions assemble at the drain contact as shown in the top panel of Fig. 5b. The potential energy at the drain contact switches from upward to downward (the bottom panel of Fig. 5b, e). The Fermi-level of the drain contact is located at the energy inside the band gap of the channel so that hole tunneling from the drain contact is limited by the Schottky junction as shown in Fig. 5e. The current is saturated even with increasing the V_ds. This pinch-off behavior is also seen in conventional transistors.

Finally, in the ambipolar region, the net ion density changes gradually from the cation dominant to the anion dominant from the source to the drain at the interface attached to WSe₂ as shown in Fig. 5c. We find that anions assembled at the drain contact pull down the potential energy around the contact. By increasing V_ds, the anions screens hole inside WSe₂ which makes the Schottky barrier thinner enough for holes to tunnel through. Furthermore, the Fermi energy of the drain contact goes below the top of the valence band in the channel at the metal-WSe₂ junction. Then, there are enough holes to tunnel through the Schottky barrier from the drain contact as depicted in Fig. 5f, which results in the p–n junction. In the p–n junction induced by IL, the drift and diffusion currents always move in the same direction. It means that the p–n junction exists only for the forward bias voltage higher than the built-in potential.

The ambipolar behavior does not occur for the conventional metal-oxide-semiconductor (MOS) transistors with the same V_ds. In the Section III of the Supplementary information, we show the current and band profile of the WSe₂ MOS transistor, whose oxide layer has the same permittivity with IL (Supplementary Fig. 2a). To fix the carrier concentration to the same order to the ion-gated transistors, we set the gate voltage to V_gs = 10 V so that n ~ 5 × 10¹³ cm⁻² at the equilibrium condition. The current increases monotonously with V_ds and the transistor is always n-type as shown in Supplementary Fig. 2b. Supplementary Fig. 3 is the band profile for the MOS transistor. The potential energy decreases linearly at the channel region by applying V_ds and the Schottky barrier at the drain area becomes perfect contact for electrons to pass through from WSe₂ to the metal. The Fermi energy of the metal contact is located inside the band gap so that the holes cannot pass through the barrier. Thus, the drain contact keeps acting as n-type contact and the current holds unipolar up to V_ds = 4 V.

Figure 6 displays the spatial distributions of the net carriers, electrons, and holes at the channel area for the linear region (a: V_ds = 0.5 V), saturation region (b: V_ds = 2.5 V), and ambipolar region (c: V_ds = 4 V). In the linear region, the electron density slightly varies around n ~ 4 × 10¹³ cm⁻². In the saturation region, on the other hand, the electron densities are not constant anymore, and a depletion point appears at the drain contact. There are a few numbers of holes as shown in the inset of Fig. 6b (p ~ 10⁸ cm⁻²) which is injected from the drain contact by the thermionic transport although the hole tunneling is prohibited in the saturation region. In the ambipolar region, electrons and holes are spread throughout the whole channel area so that small difference between the electron and hole concentrations make the p-n junction. Therefore, the electrons and holes can recombine in the whole area of the channel as shown in the Supplementary Fig. 1 of the Supplementary information (Section II). There is no depletion region when the applied voltage is higher than the built-in potential. Then, the potential drop at the p–n junction is determined by the recombination zone. The size for the recombination zone is estimated to be $1/\sqrt{\beta /{D}_{{\rm{n}}}\max [p(x)]} \sim$ 1 μm in our case. Thus, the channel size we consider is much smaller than the recombination region. It leads to no potential change at the cross-section between n and p regions.

Fig. 6: Electron concentration, n(x) (dashed line), hole concentration, p(x) (dot-dashed line), and net carrier concentration, n(x) − p(x) (solid line) inside the channel.

The three panels are for a V_ds = 0.5 V, b V_ds = 2.5 V, c V_ds = 4 V, respectively. For b, the hole concentration is plotted in the inset. For c −p(x) is plotted instead of p(x).

The application of the ion-gated TMD transistors can be very broad, stemming from light emitting devices^13,57, superconductivity⁵⁸, to thermoelectric properties⁵⁹. Here, we pick up transistors that emits circularly polarized light owing to the peculiar electronic structure of TMDs. Since there has been no simulation model constructed in this area, the essential physical factor in determining the performance of the light-emitting device is yet not known. This simulation method is advantageous to explore the crucial factors and design the ideal device structure. We can examine the characteristics of light emission by calculating the recombination rate, as demonstrated in Section II of Supplementary Information. In the simulation, the parameters presented in Table 1 can be tuned to explore the crucial factors. These factors can also be realized in experiments by changing the materials and device structures.

In conclusion, we have developed the DD model for the ion-gated TMD transistors and explained the characteristic transport behavior of the ion-gated WSe₂ transistors. We adopt the DD model coupled to the Poisson equation for calculating the band profile, carrier densities, and current. In the Poisson equation, the model including the screening effect of charge is employed to derive the potential profile of the IL. In the DD model, the generalized Einstein relation is considered for high carrier densities and the model of the practical Schottky contact is employed for considering the Schottky and Ohmic behavior of the transistors. One of the peculiar features of ion-gated transistors of 2D materials is the ambipolar behavior with the application of the gate voltage comparable to the band gap energy. The simulation explains the fundamental physics underneath for ambipolar transport and the formation of p–n junctions in the channel. The present result indicates that the DD model coupled with the Poisson equation is a fascinating tool to study ion-gated transistors. By including the spin, valley, and optical degree of freedom to the DD model, we can examine the functionality and to design the device structure of ion-gated transistors.

Methods

We introduce the concrete explanation of the models. In the DD equation, Eqs. (3) and (4), D_n(p)(x) is not described using the ordinary Einstein relation since the Boltzmann distribution is not satisfied in the considered system due to the high carrier concentration above 10¹³ cm⁻². Then, we adopt the generalized Einstein relation for the DD model⁴⁷. The generalized Einstein relation which obeys the Fermi distribution is expressed as

$${D}_{{\rm{n}}({\rm{p}})}(x)={g}_{{\rm{n}}({\rm{p}})}(x)\frac{{k}_{{\rm{B}}}T}{q}{\mu }_{{\rm{n}}({\rm{p}})},$$

(8)

where

$${g}_{{\rm{n}}}(x)=\frac{1}{{k}_{{\rm{B}}}T}n(x){\left[\frac{\partial n(x)}{\partial {\varphi_{n}}(x)}\right]}^{-1},$$

(9)

$${g}_{{\rm{p}}}(x)=\frac{1}{{k}_{{\rm{B}}}T}p(x){\left[\frac{\partial p(x)}{\partial {\varphi }_{p}(x)}\right]}^{-1}.$$

(10)

Here, φ_n(p) is the quasi Fermi potential of electrons (holes). k_B is the Boltzmann constant, and T is the temperature. Note that g_n(p) = 1 for the ordinary Einstein relation.

For realizing the practical Schottky contact, we consider the thermionic current and tunnel current passing through the metal-TMD junctions. For the thermionic current density of electrons at the source (drain) contact is written as

$${J}_{{\mathrm{thermionic}}-{\mathrm{e}}}({x}_{{\mathrm{s}}({\rm{d}})})=\pm {A}_{2{\mathrm{D}}-{\mathrm{e}}}{T}^{3/2}\left[{{\mathcal{F}}}_{1/2}\left(-\frac{{E}_{{\mathrm{c}}}(x)-{\varphi }_{{\mathrm{n}}}(x)}{{k}_{{\mathrm{B}}}T}\right)-{{\mathcal{F}}}_{1/2}\left(-\frac{{E}_{{\mathrm{c}}}(x)-{\varphi }_{{\mathrm{metal}}-{\mathrm{s}}({\mathrm{d}})}}{{k}_{{\mathrm{B}}}T}\right)\right],$$

(11)

while the thermionic current density of holes is

$${J}_{{\mathrm{thermionic}}-{\mathrm{h}}}({x}_{{\mathrm{s}}({\mathrm{d}})})=\mp {A}_{2{\mathrm{D}}-{\mathrm{h}}}{T}^{3/2}\left[{{\mathcal{F}}}_{1/2}\left(\frac{{E}_{{\mathrm{v}}}(x)-{\varphi }_{{\mathrm{p}}}(x)}{{k}_{{\mathrm{B}}}T}\right)-{{\mathcal{F}}}_{1/2}\left(\frac{{E}_{{\mathrm{v}}}(x)-{\varphi }_{{\mathrm{metal}}-{\mathrm{s}}({\mathrm{d}})}}{{k}_{{\mathrm{B}}}T}\right)\right].$$

(12)

Here, ${{\mathcal{F}}}_{1/2}$ is the Fermi integral

$${{\mathcal{F}}}_{j}(\eta )=\frac{1}{\Gamma (j+1)}{\int }_{0}^{\infty }\frac{{\xi }^{j}d\xi }{1+{e}^{\xi -\eta }},$$

(13)

where Γ(x) is the gamma function. A_2D is the Richardson constant for the 2D materials⁶⁰,

$${A}_{2{\rm{D}}-{\rm{e}}({\rm{h}})}=2\times q\frac{{(8\pi {k}_{{\rm{B}}}^{3}{{\rm{m}}}_{{\rm{e}}({\rm{h}})}{{\rm{m}}}_{0})}^{1/2}}{{h}^{2}}[{\rm{A}}/({\rm{cm}}{{\rm{K}}}^{2/3})].$$

(14)

E_c(x) and E_v(x) denote the energy at the bottom of the conduction band and the top of the valence band, respectively. φ_metal−s(d) is the Fermi energy of the source (drain) metal contact. Two is the factor stemmed from the valley degree of freedom of the monolayer TMD. We should mention that the thermionic current is considered only at the junction between the source (or drain) contact and channel, x_s(x_d). The tunnel current densities at x from source (drain) contact for electrons and holes are written as

$$\begin{array}{ll}\displaystyle{J}_{{\rm{tunnel}}-{\rm{e}}-{\rm{s}}({\rm{d}})}(x)=\pm\! \displaystyle\frac{{A}_{2{\rm{D}}-{\rm{e}}}{T}^{1/2}}{{k}_{{\rm{B}}}}\displaystyle{\int }_{{E}_{{\rm{c}}}({x}_{{\rm{s}}({\rm{d}})})}^{{E}_{{\rm{c}}}(x)}d\epsilon \left[{{\mathcal{F}}}_{-1/2}\left(\displaystyle-\frac{\epsilon -{\varphi }_{{\rm{n}}}(x)}{{k}_{{\rm{B}}}T}\right)\right.\\ \left.-\,{{\mathcal{F}}}_{-1/2}\displaystyle\left(-\frac{\epsilon -{\varphi }_{{\rm{metal}}-{\rm{s}}({\rm{d}})}}{{k}_{{\rm{B}}}T}\right)\right]{T}_{{\rm{e}}-{\rm{s}}({\rm{d}})}(\epsilon ),\end{array}$$

(15)

and

$$\begin{array}{ll}\displaystyle{J}_{{\mathrm{tunnel}}-{\mathrm{h}}-{\mathrm{s}}({\mathrm{d}})}(x)=&\mp \displaystyle\frac{{A}_{2{\mathrm{D}}-{\mathrm{h}}}{T}^{1/2}}{{k}_{{\mathrm{B}}}}\displaystyle{\int }_{{E}_{{\mathrm{v}}}({x}_{{\mathrm{s}}({\mathrm{d}})})}^{{E}_{{\mathrm{v}}}(x)}d\epsilon \left[{{\mathcal{F}}}_{-1/2}\left(\frac{\epsilon -{\varphi }_{{\mathrm{p}}}(x)}{{k}_{{\mathrm{B}}}T}\right)\right.\\ &\left.-{{\mathcal{F}}}_{-1/2}\displaystyle\left(\frac{\epsilon -{\varphi }_{{\mathrm{metal}}-{\mathrm{s}}({\mathrm{d}})}}{{k}_{{\mathrm{B}}}T}\right)\right]{T}_{{\mathrm{h}}-{\mathrm{s}}({\mathrm{d}})}(\epsilon ),\end{array}$$

(16)

respectively, where T_e−s(d)(ϵ) and T_h−s(d)(ϵ) are the transmission probability of the electrons and holes tunneling through the source (drain) contact and channel derived by the WKB approximations written as

$$\begin{array}{l}{T}_{{\rm{e}}-{\rm{s}}({\rm{d}})}(\epsilon )=\exp \displaystyle\left\{-\frac{4\sqrt{2{{\rm{m}}}_{{\rm{e}}}{{\rm{m}}}_{0}}{\left[{E}_{{\rm{c}}}({x}_{{\rm{s}}({\rm{d}})})-\epsilon \right]}^{3/2}}{3q\hslash | E(x)| }\right\},\\ {T}_{{\rm{h}}-{\rm{s}}({\rm{d}})}(\epsilon )=\exp \displaystyle\left\{\frac{4\sqrt{2{{\rm{m}}}_{{\rm{e}}}{{\rm{m}}}_{0}}{\left[{E}_{{\rm{v}}}({x}_{{\rm{s}}({\rm{d}})})-\epsilon \right]}^{3/2}}{3q\hslash | E(x)| }\right\},\end{array}$$

(17)

respectively. Here, E(x) = −dΦ(x, 0)∕dx is the electric field in the x direction. Note that T_e−s(d)(ϵ) and T_h−s(d)(ϵ) are finite only when the arguments inside the exponential functions are negative. In the numerical calculation, the Fermi integral ${{\mathcal{F}}}_{1/2}$ and ${{\mathcal{F}}}_{-1/2}$ has been obtained by using the approximation method based on the Sommerfeld expansion⁶¹. The electron (hole) current injected from contacts is included in the current continuity equation through the recombination rate as

$${R}_{{\rm{n}}({\rm{p}})-{\rm{con}}}(x)=\left\{\begin{array}{ll}\pm \frac{\rm{d{J}}_{{\rm{thermionic}}-{\rm{e}}({\rm{h}})}(x)}{\rm{dx}}&(x={x}_{{\rm{s}}})\\ \pm \frac{\rm{d{J}}_{{\rm{tunnel}}-{\rm{e}}({\rm{h}})-{\rm{s}}}(x)}{\rm{dx}}\pm \frac{\rm{d{J}}_{{\rm{tunnel}}-{\rm{e}}({\rm{h}})-{\rm{d}}}(x)}{\rm{dx}}&({x}_{{\rm{s}}}\;<\;{x}_{{\rm{d}}})\\ \pm \frac{\rm{d{J}}_{{\rm{thermionic}}-{\rm{e}}({\rm{h}})}(x)}{\rm{dx}}&(x={x}_{{\rm{d}}}).\\ \end{array}\right.$$

(18)

The total recombination term is written as R(x) = R_dir(x) + R_SRH(x) + R_n(p)−con(x).

The ion distributions in the Poisson equation, Eq. (7), are expressed as

$${i}^{+}(x,z)={n}_{s}\frac{\exp [-\frac{q{\Phi }^{\prime}(x,\,z)}{{k}_{{\rm{B}}}T}]}{1+2\gamma \;{\sinh }^{2}\frac{q{\Phi }^{\prime}(x,\,z)}{2{k}_{{\rm{B}}}T}},$$

(19)

and

$${i}^{-}(x,z)={n}_{s}\frac{\exp [\frac{q{\Phi }^{\prime}(x,\,z)}{{k}_{{\rm{B}}}T}]}{1+2\gamma \;{\sinh }^{2}\frac{q{\Phi }^{\prime}(x,\,z)}{2{k}_{{\rm{B}}}T}}.$$

(20)

γ is the screening parameter of the ions stemmed from the finite size of ions. $\gamma ={n}_{{\rm{i}}}/{n}_{\max }$ where ${n}_{\max }$ is the maximum concentration of both cation and anion which can pack in the liquid. Here we define shifted potential, ${\Phi }^{\prime}(x,z)$, since Φ(x, z) is set to be zero reference to the Fermi energy of the source contact. ${\Phi }^{\prime}(x,z)$ and the coefficient of carrier concentration, n_s, are determined to satisfy the condition

$${\int _{\rm{A}_{\rm{ion}}}}{i}^{+}(x,z){\mathrm{d}}x{\mathrm{d}}z={\int _{\rm{A}_{\rm{ion}}}}{i}^{-}(x,z){\mathrm{d}}x{\mathrm{d}}z=\int \frac{{n}_{{\rm{i}}}}{2}{\mathrm{d}}x{\mathrm{d}}z,$$

(21)

where A_ion is the area of the ion. Note that the average carrier concentration, n_i, is constant since there is no electrodes to supply ions in the system.

In the numerical calculation, the Scharfetter-Gummel discretization is used for solving the DD equation which is described in the Section I of the Supplementary information.