Introduction

In many papers [1,2,3,4,5,6,7,8,9] describing the inner structure of spherulites grown by slow cooling of the melt, many investigators proposed that stacked lamellae grow continuously along the radial direction from the center of the spherulite with twisting of the lamellae around a special crystal axis. One of the most well-known examples is observed in the spherulite of the orthorhombic polyethylene [10,11,12]. The lamellar growth occurs along the radial direction parallel to the b axis, and the lamellar normal twists periodically around this b axis. In other words, the a and c axes are rotated periodically around the b axis [3, 5]. The period of this lamellar rotation corresponds to the spacing of the ring pattern observed by a polarized optical microscope (POM) [5]. This type of lamellar twisting phenomenon has been proposed for various types of polymers [10,11,12]. In other polymers, however, no periodic ring pattern is observed on the top surface of the spherulites, suggesting that the lamellae do not twist around the radial direction; a typical case is seen for isotactic or syndiotactic polypropylene [13].

The interpretation of the repeated ring patterns is made on the basis of the concept of the lamellar twisting phenomenon [1, 4, 6, 9,10,11,12, 14] and/or the rhythmic growth mechanism [15,16,17,18,19,20]. Currently, the former concept or the lamellar twisting model seems to be a major trend because the twisting phenomenon has been observed for various types of polymers using a powerful micron-sized synchrotron X-ray beam [21,22,23,24,25,26]. However, an intellectual question to be asked is whether the lamellar twisting is essential or only the pre-requisite for the generation of such periodic patterns.

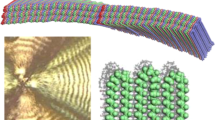
One important point to note is that the lamellar twisting has been believed for a long time to occur continuously from the center to the periphery without any discontinuity, as proposed for polyethylene (PE). For all kinds of polymers showing ring patterns, do the lamellae grow continuously from the nuclei to the periphery through the twisting mode? Poly(ethylene adipate) (PEA), the focus of the present study, was also believed to be in the same situation: it shows a beautiful ring pattern, as observed in Fig. 1, for which many investigators have proposed the continuous twisting model [14] similar to that applied to PE banded spherulites. Recently, however, by observing the fractured surface (i.e., the interior of the lamellar assembly) of the PEA spherulite using an atomic force microscope (AFM) and scanning electron microscope (SEM), Woo et al. [27,28,29] discovered that the interiors of the ring-banded PEA spherulites are composed of a discontinuous structure of aggregated blocks. As shown in Fig. 1, they proposed a model composed of a periodic and alternative array of flat-on lamellae (almost horizontally laid lamellae or radial lamellae) and edge-on lamellae (almost vertically standing lamellae or tangential lamellae) along the radial direction [27]. The periodic aggregation of these blocks corresponds to the observed ring pattern. Since the observed size of these blocks is on the micrometer scale, these observations do not necessarily clearly indicate (i) whether twisting of the lamellae occurs inside the blocks (flat-on lamellae) and (ii) whether the edge-on lamellae (tangential lamellae) in their papers are truly the aggregation of crystalline lamellae.

Fig. 1
figure 1

a POM image, b, c SEM images of a spherulite of poly(ethylene adipate), and d schematic model of the cross section of the spherulite. The graphs (b–d) are quoted from ref. 27. [copyright permission granted by ACS]

Full size image

To answer these questions and clarify the relation between the observed ring pattern and aggregated lamellar structure in the PEA spherulite, it is useful to observe the inner structure of the spherulite by performing wide-angle X-ray diffraction (WAXD) and small-angle X-ray scattering (SAXS) measurements. Of course, the X-ray beam incident on the spherulite must be small enough to detect the local structures. In the present paper, we measured the local microstructures using a micron-sized synchrotron X-ray beam. Since Fujiwara [5] reported the twisting phenomenon of the polyethylene lamellae about the b axis using a micron-sized X-ray beam, utilization of a micron-sized X-ray beam in the study of the inner structure of spherulites has been reported in many papers [21,22,23,24,25,26]. However, the present paper may be unique in the following point: as will be described in a later section, the lamellae were found to twist 180° continuously around the radical axis. However, this continuous lamellar twisting must be stopped discontinuously once at the boundary between the neighboring lamellar blocks, as determined from the spherulite image shown in Fig. 1. Our purpose is to clarify the detailed relation between the two keywords “continuous” and “discontinuous”. How is the discontinuity of the growing lamellae at the boundaries related to the lamellar twisting phenomenon?

In the present paper, we describe the quantitative analysis of WAXD/SAXS data collected simultaneously from various positions of a PEA spherulite and then propose a model to solve the above-mentioned complicated hierarchical structure.

Experimental

Material and sample preparation

PEA samples were purchased from Aldrich Inc. The average molecular weight measured by gel permeation chromatography (GPC) was ~10,000 g/mol. The sample was dissolved in chloroform and cast at room temperature on a SiN thin film supported by a Si plate frame. The average thickness of the thus-obtained thin film was ~12 μm. (Thicker films were also used in the X-ray scattering measurement, but diffraction patterns resulting from partially overlapped spherulites were detected.) The films were melted above the melting point (ca. 55 °C) and brought to constant temperature (28 °C) to induce isothermal crystallization of the spherulites.

Measurements

The simultaneous measurement of the two-dimensional WAXD and SAXS patterns was performed at beamline BL03XU in SPring-8, Harima, Japan. As shown in Appendix A, an X-ray beam with an effective diameter of 8 μm, produced using a pinhole, was used first. The sample was shifted stepwise at a 20 μm pitch. The obtained WAXD and SAXS patterns did not show any change, including in the relative intensity between the diffraction spots, although the direction of the spots was rotated depending on the azimuthal angle. The lack of change in the diffraction pattern was considered to result from the X-ray beam size being too large to separate the originally different scattering patterns of the neighboring blocks repeated at a 7 μm period. Then, an X-ray beam with a half-width of 1.1 μm was produced with a Fresnel zone plate (FZP) and used as the incident beam. The thus-obtained micron-sized X-ray beam was focused on the sample surface. A snapshot of the measurement system is shown in Fig. 2. The wavelength of the X-ray beam was 1.31 Å. The SiN sample holder was set into a metal holder. In the X-ray scattering measurements, this holder was moved stepwise along the horizontal and vertical directions at a 1 μm pitch using computer-controlled servomotors. The sample position irradiated by the incident X-ray beam was monitored using an optical microscope. The WAXD and SAXS data were collected simultaneously using an external trigger. The WAXD patterns were detected with a flat panel detector (Hamamatsu Photonics Co., Japan) set approximately 4 cm from the sample position. The SAXS patterns were measured using an image-intensifier CCD detector (Hamamatsu Photonics Co., Japan) set ~60 cm apart from the sample position. The X-ray exposure time was 1 s for one shot.

Fig. 2
figure 2

a Snapshot of the simultaneous WAXD/SAXS measurement system set up in the SPring-8 03XU beamline. b The X-ray beam and Fresnel zone plate. c Scanning route of the X-ray beam along the radial direction of the PEA spherulite

Full size image

Results and discussion

X-ray data analysis

As shown in Fig. 1, the pitch of a series of rings is ~7 μm along the radial direction. Simultaneous WAXD and SAXS measurements were performed at various positions with each 1 μm pitch for the spherulite sample, the results of which are shown in Fig. 3. The WAXD and SAXS patterns were almost the same at the various positions, but the relative intensity of the observed scattering peaks was found to change periodically depending on the measurement position. Figure 3c shows the position dependence of the WAXD intensities, which were evaluated by integration over some regions. The relative intensity changes periodically, and the maximal intensity position is different among the observed reflections. For example, the 020 and 11\(\bar 1\) reflections showed maxima around positions # 4 and 11, while the 110 reflection showed double maxima around positions # 3 and 5. The SAXS intensity showed a maximum at position #8 and a minimum at position #4, indicating that the lamellar normal was oriented parallel to the incident X-ray beam at position #4 and perpendicular at position #8.

Fig. 3
figure 3

a POM image of the PEA spherulite and magnified area. b WAXD and SAXS patterns measured at the various positions shown in a. c The position dependence of the integrated intensity estimated for the various scattering peaks. The position number and distance (μm) correspond to each other because the pitch of the WAXD and SAXS measurements was 1 μm/shot. The symbols α, β, γ, and δ indicate the order of appearance of the reflection during the twisting of lamellae from the inside to the outside direction of the spherulite, corresponding to the right-handed screw motion (refer to Fig. 6)

Full size image

The WAXD data can be interpreted reasonably by referring to the crystal structure information of PEA [30,31,32]. This polymer has two types of crystal structures, the α and β forms. From the X-ray diffraction data, the present spherulite is known to take the α form with the crystal structure shown in Fig. 4. The real and reciprocal lattices are also drawn in this figure. (To confirm the crystal structure shown in Fig. 4, we performed crystal structure analysis using the newly measured two-dimensional X-ray diffraction data.)

Fig. 4
figure 4

Crystal structure of the α form of PEA [30,31,32]. The crystal belongs to the monoclinic system with space group P21/a. The corresponding reciprocal lattice is also shown here

Full size image

The real cell a = 5.47 Å, b = 7.23 Å, c (chain axis) = 11.72 Å, and β = 113.5°

The reciprocal cell a* = 0.200 Å−1, b* = 0.138 Å−1, c* = 0.093 Å−1, and β* = 66.5°

The observed WAXD peaks can be indexed to the reciprocal lattice points 020, 110 (1\(\bar 1\)0), and 11\(\bar 1\). The different maximal intensity positions among these reflections can be interpreted using the concept of the Ewald sphere on the basis of the twisted lamellar structure model, as will be described below. There might be another type of structure model in which the thickness or density of the aggregated crystalline parts changes periodically (binarily) without any lamellar twisting. However, the latter model should give the intensity maxima at the same positions for all the observed X-ray diffraction peaks, inconsistent with the experimental data shown in Fig. 3c.

Keith studied the crystal axis in the radial direction of the PEA spherulite but, at that time, could not determine whether the b axis is perpendicular or parallel to the radial direction [2]. After many trials, we have found that rotation of the crystallite occurs around the a axis. (This can be confirmed if the h00 diffraction spots are detected and if their intensities do not change at any position of the spherulite. However, the present data could not detect these peaks.) The equations necessary for interpretation of the experimental data shown in Fig. 3 are derived under the assumption of twisting around the a axis. The Cartesian coordinate system is defined in such a way that the c* is parallel to the Z axis and the b* is parallel to the Y axis at the starting point, as shown in Fig. 5. The rotation axis is the X axis or the a axis. The initial vectors of the a*, b*, and c* axes are expressed below on the basis of the XYZ Cartesian coordinate system.

$${{\boldsymbol{a}}^ \ast {\mathrm{ = }}\left( {\begin{array}{*{20}{c}} {0.183} \\ {0.000} \\ {0.080} \end{array}} \right){\AA}^{ - 1}\quad {\boldsymbol{b}}^ \ast {\mathrm{ = }}\left( {\begin{array}{*{20}{c}} {0.000} \\ {0.138} \\ {0.000} \end{array}} \right){\AA}^{ - 1}\quad {\boldsymbol{c}}^ \ast {\mathrm{ = }}\left( {\begin{array}{*{20}{c}} {0.000} \\ {0.000} \\ {0.093} \end{array}} \right){\AA}^{ - 1}}$$
(1)

Therefore, the initial vectors of the reciprocal lattice points are given as follows.

$${\boldsymbol{p}}^ \ast \left( {020} \right){\mathrm{ = 2}}{\boldsymbol{b}}^ \ast {\mathrm{ = }}\left( {\begin{array}{*{20}{c}} {0.000} \\ {0.276} \\ {0.000} \end{array}} \right){\AA}^{ - 1}$$
(2)
$${\boldsymbol{p}}^ \ast \left( {110} \right){\mathrm{ = }}\,{\boldsymbol{a}}^ \ast + {\boldsymbol{b}}^ \ast { = }\left( {\begin{array}{*{20}{c}} {0.183} \\ {0.138} \\ {0.080} \end{array}} \right){\AA}^{ - 1}$$
(3)
$${\boldsymbol{p}}^ \ast \left( {0\bar 10} \right){\mathrm{ = }}\,{\boldsymbol{a}}^ \ast - {\boldsymbol{b}}^ \ast {\mathrm{ = }}\left( {\begin{array}{*{20}{c}} {0.183} \\ { - 0.138} \\ {0.080} \end{array}} \right){\AA}^{ - 1}$$
(4)
$${\boldsymbol{p}}^ \ast \left( {11\bar 1} \right){\mathrm{ = }}\,{\boldsymbol{a}}^ \ast + {\boldsymbol{b}}^ \ast - {\boldsymbol{c}}^ \ast {\mathrm{ = }}\left( {\begin{array}{*{20}{c}} {0.183} \\ {0.138} \\ { - 0.013} \end{array}} \right){\AA}^{ - 1}$$
(5)

In Fig. 5, an Ewald sphere is also drawn. The reflection can be detected when the corresponding reciprocal lattice point crosses the surface of the Ewald sphere. To satisfy this condition, the reciprocal lattice point must be rotated at the corresponding angle. The crystallite is rotated by angle ϕ around the a axis (or the X axis), and then, the vector of the rotated reciprocal lattice point p* is expressed below using the rotation matrix R.

$${\boldsymbol{p}}^ \ast \prime = {\boldsymbol{Rp}}^ \ast = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 0 \end{array}\quad \begin{array}{*{20}{c}} 0 \\ c \\ s \end{array}\quad \begin{array}{*{20}{c}} 0 \\ { - s} \\ c \end{array}} \right)\left( {\begin{array}{*{20}{c}} {X_{\mathrm{p}}} \\ {Y_{\mathrm{p}}} \\ {Z_{\mathrm{p}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {X_{\mathrm{p}}} \\ {cY_{\mathrm{p}} - sZ_{\mathrm{p}}} \\ {sY_{\mathrm{p}} + cZ_{\mathrm{p}}} \end{array}} \right)$$
(6)

where c = cos(ϕ) and s = sin(ϕ). The equation to express the Ewald sphere is given as follows (refer to Fig. 5). The origin of the sphere is at (0, 0, 1/λ), and the radius is 1/λ.

$$X^2{\mathrm{ + }}Y^2{\mathrm{ + }}\left( {Z - 1/\lambda } \right)^2 = \left( {1/\lambda } \right)^2$$
(7)

where λ is the wavelength of the incident X-ray beam. The rotated reciprocal lattice point needs to satisfy Eq. 7.

$$X_{\mathrm{p}}^2 + \left( {cY_{\mathrm{p}}-sZ_{\mathrm{p}}} \right)^2 + \left( {sY_{\mathrm{p}} + cZ_{\mathrm{p}}-1/\lambda } \right)^2 = \left( {1/\lambda } \right)^2$$
(8)

Using all of these vectors and matrices, we can predict the rotation angles ϕ of the observed reflection peaks. For example, in the case of the p*(020) vector, the substitution of Eq. 2 into Eq. 8 gives the rotation angle ϕ020.

$$\phi _{020} = 10.4^\circ$$

Similarly, the angles for the other reciprocal lattice points are evaluated to be as follows.

$$ \begin{array}{*{20}{c}} {\phi _{0\bar 20} = 190.4^\circ } \\ {\phi _{\bar 110} = 196.0^\circ } \end{array}\quad \begin{array}{*{20}{c}} {\phi _{110} = - 16.0^\circ } \\ {\phi _{11\bar 1} = 9.0^\circ } \end{array}\quad \begin{array}{*{20}{c}} {\phi _{\bar 1\bar 10} = 164.0^\circ } \\ {\phi _{\bar 1\bar 11} = 189.0^\circ } \end{array}\quad \begin{array}{*{20}{c}} \\ {\phi _{1\bar 10} = 16.0^\circ } \\ {} \end{array}$$

Here, we note that the lattice planes 110, \(\bar 1\)10, 1\(\bar 1\)0, and \(\bar 1\)\(\bar 1\)0 are equivalent, as is known from the space group symmetrical relation. Similarly, planes 11\(\bar 1\) and \(\bar 1\)\(\bar 1\)1 are equivalent. Figure 6 summarizes the thus-calculated angles ϕ of these various reflections. The a axis directs outward from the spherulite center, and the rotation angle ϕ increases in the order of 110 (−16.0°), 11\(\bar 1\) (9.0°), 020 (10.4°), and 1\(\bar 1\)0 (16.0°), which corresponds to the α, β, γ, and δ peak positions shown in Fig. 3 or the local positions #5, 4, and 3, respectively. This clearly indicates that the lamellar twisting occurs dextrorsely (in a right-handed screw mode). Since the maximal intensity points are repeated at positions #4 and 11, i.e., with a spacing of 7 point intervals, the rotation angle between the two neighboring measurement positions can be estimated as 180°/7 = 25.7°. This value is coincident with the difference in the maximal peak position, ~26°, between the 020 (#4) and 110 reflections (#3 and 5).

Fig. 5
figure 5

Illustration showing the Bragg reflection that occurs upon crossing of the reciprocal lattice point with the Ewald sphere

Full size image
Fig. 6
figure 6

a The rotation angles ϕ predicted for the various reciprocal lattice points and b their corresponding location on the spherulite. The rotation axis is parallel to the a axis, the vector of which directs to our side. The rotation is ordered as α, β, γ, and δ. That is, the lamellar twisting occurs similar to a right-handed screw along the outward direction from the spherulite center (refer to Fig. 3)

Full size image

As already noted, the SAXS intensity showed a maximum at position #8 and a minimum at position #4. Therefore, it can be said that the lamellar normal is oriented parallel to the incident X-ray beam at position #4 and perpendicular at position #8. Figure 7 shows the relation between the twisting of the stacked lamellae and the rotation of the unit-cell structure. At position #4, the lamellar surface is parallel to the spherulite surface. The lamellae are twisted gradually in a right-handed direction about the outward radial axis (or the positive direction of the a axis). At position #1 (and also at position #8), the lamellae stand almost vertically, i.e., the lamellar normal vector is parallel to the spherulite surface and perpendicular to the radial axis. The WAXD data analysis indicated that the c* axis (or the chain axis) is parallel to the spherulite surface at positions #7 and 8. By combining the WAXD and SAXS data analysis, we can clearly see that the chain axis (the c axis) is parallel to the lamellar normal. This is quite reasonable if the chain-folded lamellar structure is assumed for this polymer. The evaluated long period between the stacked lamellae was ~128 Å. Figure 7 includes this situation in a concrete manner. More precisely, the chain axis is tilted by ~24° from the lamellar normal, as understood from the relation between the c and c* axes (Fig. 4). The thus-clarified inner structure can be further related to the optical microscope image. In Fig. 3, the bright zone corresponds to positions #1 and 8, and the dark zone corresponds to positions #4 and 11.

Fig. 7
figure 7

The twisting of the crystal lattice around the a axis and the twisted lamellar structure. Position #4 corresponds to the horizontally oriented lamellar surface, and position #8 corresponds to the vertically standing lamellar surface (refer to Fig. 3)

Full size image

Twisting and discontinuity of stacked lamellae

Thus far, we have discussed the characteristics of the inner structure of the PEA spherulites viewed from the X-ray scattering data analysis. On the other hand, Woo et al. [27] reported discontinuous aggregations of blocks inside the PEA spherulites. These two independently obtained experimental results are combined to create a new model of lamellae aggregation in the PEA spherulite, as shown in Figs. 8 and 9. The following several points need to be taken into consideration to propose the illustration given in Figs. 8 and 9.

Fig. 8
figure 8

a Illustration of the stacking structure of the twisted lamellae viewed from the surface normal to the spherulite, b illustration of the stacked lamellar plates with the long period (LP), and c the actually observed SAXS patterns at positions #1, 4, and 8 (refer to Fig. 3), where the X-ray beam is incident from the direction normal to the paper, as shown by the blue bold arrows and red double circles

Full size image
Fig. 9
figure 9

Illustration of the twisted lamellae: a the continuously growing lamellar model and b the discontinuously connected lamellae with irregular boundaries between the neighboring lamellae. The disordered zones correspond to the uneven parts of the spherulite surface (refer to Fig. 1)

Full size image

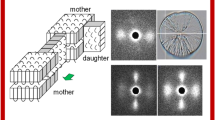
The PEA spherulite discussed earlier by Woo et al. [27] had a film thickness of ~50 μm, while that in this study had a thickness of ~12 μm. The difference in the thickness may, strictly speaking, give a different temperature gradient along the thickness direction, resulting in the formation of spherulites with different inner structures. However, this possibility can be reasonably discarded by considering the following experimental facts: (i) the spherulite was isothermally grown at the same temperature (28 °C), (ii) the observed ring pattern period was also the same, (iii) the optical birefringence of the spherulite is commonly negative, and (iv) the spherulite can be cracked relatively easily into arc-shaped fragments along the ring edge. Figure 10 shows the POM image of PEA spherulites with cracked edges. The spherulites were cracked and fell out along the ring edges.

Fig. 10
figure 10

The cracked edges of the PEA spherulites. The edges are cracked along the rings of the spherulites. This is consistent with the images shown in Figs. 8a and 9b

Full size image

Figure 8 shows the relation between the twisted lamellae and aggregation of the crystal planes. At positions #1 and 8, the crystal planes of the folded chain stems aggregate to form lamella [Fig. 8a]. Many crystal planes gather in a span of several micrometers to form the long lamellar edge [Fig. 8b]. The thus-created lamellae are stacked with a long period of 128 Å. The lamellae grow in a twisting mode. Therefore, when the X-ray beam is incident to the direction shown by blue bold arrows and by the red double circles, the SAXS long period peaks are detected at positions #1 and 8, while no SAXS peak is detected at position #4.

As shown in Fig. 9, these twisted lamellae are aggregated on a much larger scale and form blocks. One key point of Fig. 9 is the difference between the continuously twisted and growing lamellae (a) and the discontinuous arrangement of the 180°-twisted lamellar blocks (b). The disconnected boundary is assumed to correspond to the positions # 1 and 8 in Fig. 3. This disconnection zone might consist of structurally irregular assemblies of the chains, but the zone width should be quite narrow, possibly narrower than the resolution power of 1 μm or the effective size of the incident X-ray beam. Otherwise, the WAXD (and SAXS) would have given almost amorphous halo patterns. The irregular end zones may have a lower density than the crystalline zones and thus may protrude out of the stacked lamellar blocks, corresponding to the rough stripes detected on the spherulite surface, as shown in Fig. 1c.

As illustrated in Fig. 11, the lamellar formation process is described below on the basis of the above-mentioned X-ray diffraction data analysis combined with the AFM/STM observations [27]. The former (a) provided information about the lamellar twisting and the periodic orientation of the crystal axes. The latter (b) gives the morphology of the discontinuous blocks of aggregated lamellae. We speculate (c) that the nucleation and growth of the new lamellar blocks start at each disconnected and irregular zone. This speculation (c) is combined with the above-mentioned experimental data (a) and (b) to describe the lamellar growth process.

  1. (i)

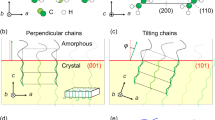
    The molecular chains are disordered in the melt. These chains attached on the substrate surface start to form folded crystalline planes (200) and grow in the direction normal to the substrate surface (the z axis in Fig. 10). The thus-created crystal plane is denoted A in this figure. This situation is speculated to occur in region #1 (Figs. 8 and 9). Precisely speaking, the normal to the (200) plane or the a* axis is tilted from the radial direction (or the a axis) by 24°. The (200) plane is used here for simplicity of the explanation without any loss of the essence.

  2. (ii)

    The surrounding chains diffuse into the surface of A and grow along the z axis and, at the same time, in the radial direction (the x axis). Then, a second plane B is formed.

  3. (iii)

    The process (ii) is repeated to grow lamella along the x axis (planes A, B, C, and so on). However, the crystal planes are rotated gradually around the x axis at a small angle of 0.007°/plane from the vertical direction of the initial plane A. (The 180° twisting of lamella occurs in a 7 μm pitch. As shown in Fig. 4, the crystal planes are assumed to grow along the a axis. The distance between the neighboring 200 planes is the a′-axial length/2 = 5.47sin(113.5°)/2 = 2.51 Å. Therefore, the rotation angle per crystalline plane is equal to (180°/7 μm) × 2.51 Å = 0.007°.) In this way, the newly formed crystal planes rotate gradually and stepwise by a quite small angle of 0.007°, but the accumulation of such a small rotation finally results in a large lamellar twisting of 180°!

  4. (iv)

    After twisting approximately 3.5 μm, the lamellar fronts reach the middle point (positions #4 and 5), and the lamellar surfaces are now flat-on the substrate; in other words, the molecular chain stems vertically along the normal to the substrate surface.

  5. (v)

    Passing through this point, the lamellae continue to grow by adsorbing the molten chains and twist further until finally reaching position #8, where the lamellae have rotated 180° when viewed from the starting point, position #1. The molecular chain stems are now attached in parallel on the substrate surface, the same as at the starting point, position #1. These chain segments are stabilized for a while due to the interaction with the substrate. Then, the molten chains surrounding them start to crystallize slowly on the substrate surface.

  6. (vi)

    These processes (i)–(v) repeat in the radial direction to form a larger spherulite. The ring pattern is observed at the 7 μm period, corresponding to periodical repetition of the 180°-twisted lamella and the narrow and irregular zone.

Fig. 11
figure 11

A model showing the growth and twisting of the crystal planes (A, B, C and so on) along the radial axis of the spherulite. The crystal planes are assumed to be the 200 planes, the normal of which is tilted by ~24o from the radial (or the a axial) direction (refer to Fig. 5.) The rotation angle of one crystal plane is 0.007° with a pitch of a′/2 = 2.51 Å. The growth rate is assumed to be slow around planes A and B and becomes faster at plane D. This figure is compared with the model shown in Figs. 8 and 9 in the range from position #1 to position #4

Full size image

This model suggests the presence of different growth rates in the spherulite. The nucleation rate at positions #1 and 8 might be slow because the molecular chain stems are adsorbed and interact with the substrate surface. On the other hand, the growth rate at positions # 4 and 5 might be relatively fast to cause the continuous growth of lamellae because of such a relatively unstable situation that the chain stems stand vertically on the surface. By assuming the rhythmical alternating change of fast and slow growth along the radial axis, Kyu et al. [15] applied the Gizburg–Landau equation (model C) derived from phase-field theory to simulate the ring pattern of the spherulite. Our above-mentioned model might be similar to their rhythmic growth idea. However, their phenomenological and mean field model did not take such a microscopically occurring lamellar twisting mode into account concretely. A concerted theory with both ideas of lamellar block discontinuity and lamellar twisting phenomenon taken into account must be developed in the future.

Before closing this paper, we note the birefringence of the PEA spherulite used in the present experiment. This spherulite shows negative birefringence in the POM image. However, Woo et al. [27, 28] reported a more complicated phenomenon. They said that the birefringence of the spherulite can be changed artificially by changing the isothermal crystallization condition. The spherulite prepared by repeated isothermal crystallizations at two alternating temperatures, i.e., from Thigh to Tlow and from Tlow to Thigh. The grown spherulite shows a ring pattern with alternating positive and negative birefringence. Originally, this polymer (PEA) does not contain asymmetric carbon atoms, but it can make the two oppositely screwed helical chains (right-handed and left-handed helices). As a result, we may have two opposite ways of lamellar twisting, right-handed and left-handed twisting, depending on the isothermal crystallization conditions. If the inverse rotation of lamellae occurs in the growth direction, the birefringence may change. Since the lamellae start to grow in the disconnected and irregular zone according to our proposed model, the possibility of the right-handed and left-handed twisting mode is 50%. The detailed mechanism to determine such a change in the twisting direction is not clear at present, but it might be determined by various factors, such as the thermal fluctuation of the molecular chains in the lamellae, the interaction with the substrate, etc. In this way, the artificial variation of the birefringence of the spherulite [27, 28] can be realized by controlling the lamellar twisting mode starting at the irregular end zone of the growing lamella. This speculation needs to be checked experimentally by combining optical microscope observations and microbeam X-ray scattering measurements.

Conclusions

The ring patterns in many banded polymers have often been interpreted using the concept of periodic twisting of continuously grown long lamellar plates. However, as Woo et al. [27] recently showed, the continuous twisting is not necessarily realized and/or not essential for banding behavior because discontinuity between the neighboring blocks exists. As described in the present paper, we investigated the finer details of the lamellar assembly phenomenon in PEA ring-banded spherulites using the powerful synchrotron microbeam X-ray scattering technique. Both the WAXD and SAXS data, which were collected simultaneously using a micron-sized X-ray beam precisely directed to closely spaced positions on the PEA lamellae, were analyzed quantitatively to show the lamellar twisting between the bright and dark zones of the spherulite.

The PEA spherulite consists of periodic aggregations of disconnected blocks with the same period as the period of the ring pattern. These blocks consist of twisted lamellar aggregations. These two observations are combined to clarify the geometrical interrelation between the lamellar twisting phenomenon and the disconnected lamellar aggregates from the various hierarchical structure levels. The thus-revealed hierarchical structure may represent a new concept for the spherulite creation mechanism, different from conventional ideas. At present, however, we have not found concrete reasons why these disconnected zones are created in the growth process of a large spherulite.

In the case of the PEA spherulite, at least, continuous and periodic twisting occurs only in the zone between the neighboring two rings, and the end parts of the neighboring lamellar blocks are not continuously connected [27]. Such views of interrupted discontinuity in the lamellae in banded spherulites were recently echoed by Schultz [33] in his re-analysis of old AFM data for ring-banded poly(3-hydroxybutyrate-co-3-hydroxyhexanoate). Future studies of the inner structure and outer morphology of many other polymer spherulites may allow us to clarify the mechanism of this peculiar phenomenon with more universal interpretations.