Abstract
It is generally believed that a generic system can be reversibly transformed from one state to another by a sufficiently slow change of parameters. Microscopically, this belief is often justified using connections to the quantum adiabatic theorem stating that there are no transitions between different energy levels if the hamiltonian changes slowly in time. Here, we show that in fact the response to such a slow change can be non-trivial in low-dimensional gapless systems. We identify three generic regimes of the response: analytic, non-analytic and non-adiabatic, which are characterized by a different behaviour of the heating induced in the system with the ramp rate. In the last regime, the limits of the ramp rate going to zero and the system size going to infinity do not commute and the adiabatic process does not exist in the thermodynamic limit. We support our results with numerical and analytical calculations.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout

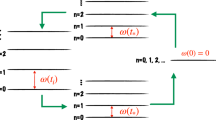
 on δ for different sizes at fixed temperature T=0.02.
on δ for different sizes at fixed temperature T=0.02.
 on δ in a two-dimensional system for two different sizes.
on δ in a two-dimensional system for two different sizes.

Similar content being viewed by others
References
Landau, L. D. & Lifshitz, E. M. Statistical Physics 1 (Butterworth-Heinemann, Oxford, 1999).
Balian, R. From Microphysics to Macrophysics (Springer, Berlin, 1991).
Sachdev, S. Quantum Phase Transitions (Cambridge Univ. Press, Cambridge, 1999).
Chaikin, P. M. & Lubensky, T. C. Principles of Condensed Matter Physics (Cambridge Univ. Press, Cambridge, 1995).
Dobrescu, B. E. & Pokrovsky, V. L. Production efficiency of Feshbach molecules in fermion systems. Phys. Lett. A 350, 154–158 (2006).
Altland, A. & Gurarie, V. Many body generalization of the Landau Zener problem. Phys. Rev. Lett. 100, 063602 (2008).
Strecker, K. E., Partridge, G. B. & Hulet, R. G. Conversion of an atomic Fermi gas to a long-lived molecular Bose gas. Phys. Rev. Lett. 91, 080406 (2003).
Polkovnikov, A. Universal adiabatic dynamics in the vicinity of a quantum critical point. Phys. Rev. B 72, 161201(R) (2005).
Zurek, W. H., Dorner, U. & Zoller, P. Dynamics of a quantum phase transition. Phys. Rev. Lett. 95, 105701 (2005).
Dziarmaga, J. Dynamics of a quantum phase transition: Exact solution of the quantum Ising model. Phys. Rev. Lett. 95, 245701 (2005).
Fubini, A., Falci, G. & Osterloh, A. Robustness of adiabatic passage through a quantum phase transition. New J. Phys. 9, 134 (2007).
Dziarmaga, J. Dynamics of a quantum phase transition in the random Ising model: Logarithmic dependence of the defect density on the transition rate. Phys. Rev. B 74, 064416 (2006).
Caneva, T., Fazio, R. & Santoro, G. E. Adiabatic quantum dynamics of a random Ising chain across its quantum critical point. Phys. Rev. B 76, 174303 (2007).
Mukherjee, V., Divakaran, U., Dutta, A. & Sen, D. Quenching dynamics of a quantum XY spin-1/2 chain in a transverse field. Phys. Rev. B 76, 174303 (2007).
Zurek, W. H. Cosmological experiments in condensed matter systems. Phys. Rep. 276, 177–221 (1996).
Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292, 472–476 (2001).
Vilenkin, A. Many Worlds in One: The Search for Other Universes (Hill and Wang, New York, 2006).
Parker, L. Quantized fields and particle creation in expanding universes. I. Phys. Rev. 183, 1057–1068 (1969); II. Phys. Rev. D 3, 346–356 (1971).
Danielsson, U. H. Lectures on string theory and cosmology. Class. Quant. Grav. 22, S1–S39 (2005).
Polkovnikov, A. Quantum corrections to the dynamics of interacting bosons: Beyond the truncated Wigner approximation. Phys. Rev. A 68, 053604 (2003).
Polkovnikov, A., Sachdev, S. & Girvin, S. M. Nonequilibrium Gross–Pitaevskii dynamics of boson lattice models. Phys. Rev. A 66, 053607 (2002).
Bloch, I., Dalibard, J. & Zwerger, W. Rev. Mod. Phys.; Preprint at <http://arXiv:0704.3011> (2008) Many-body physics with ultracold gases.
Acknowledgements
We would like to acknowledge E. Altman, E. Demler, A. Garkun, S. Girvin, V. Gurarie, M. Lukin, V. Pokrovsky and N. Prokof’ev for useful discussions. A.P. was supported by AFOSR YIP and partially by NSF under grant PHY05-51164. V.G. is partially supported by the Swiss National Science Foundation and AFOSR. A.P. also acknowledges the Kavli Institute for Theoretical Physics for hospitality.
Author information
Authors and Affiliations
Contributions
The authors have made equal contributions in preparing and writing this work.
Corresponding author
Supplementary information
Supplementary Information
Supplementary Information and Supplementary Figure 1–6 (PDF 427 kb)
Rights and permissions
About this article
Cite this article
Polkovnikov, A., Gritsev, V. Breakdown of the adiabatic limit in low-dimensional gapless systems. Nature Phys 4, 477–481 (2008). https://doi.org/10.1038/nphys963
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys963
This article is cited by
-
Quantum adiabatic cycles and their breakdown
Communications Physics (2021)
-
Quantum Speed Limits For Adiabatic Evolution, Loschmidt Echo and Beyond
International Journal of Theoretical Physics (2021)
-
Quantum many-body systems out of equilibrium
Nature Physics (2015)
-
Nonlinear quantum interferometry with Bose condensed atoms
Frontiers of Physics (2012)
-
Many-body Landau–Zener dynamics in coupled one-dimensional Bose liquids
Nature Physics (2011)