Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Goldstone mode and pair-breaking excitations in atomic Fermi superfluids

Nature Physics volume 13, pages 943–946 (2017)Cite this article

Subjects

Abstract

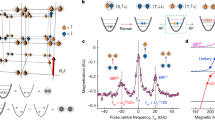
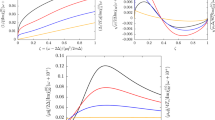
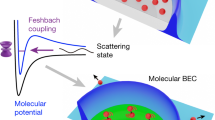
Spontaneous symmetry breaking is a central paradigm of elementary particle physics1, magnetism2, superfluidity3 and superconductivity4. According to Goldstone’s theorem, phase transitions that break continuous symmetries lead to the existence of gapless excitations in the long-wavelength limit5. These Goldstone modes can become the dominant low-energy excitation, showing that symmetry breaking has a profound impact on the physical properties of matter. Here, we present a comprehensive study of the elementary excitations in a homogeneous strongly interacting Fermi gas through the crossover from a Bardeen–Cooper–Schrieffer (BCS) superfluid to a Bose–Einstein condensate (BEC) of molecules using two-photon Bragg spectroscopy. The spectra exhibit a discrete Goldstone mode, associated with the broken-symmetry superfluid phase, as well as pair-breaking single-particle excitations. Our techniques yield a direct determination of the superfluid pairing gap and speed of sound in close agreement with strong-coupling theories.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Probing homogeneous excitation spectra with focused beam Bragg scattering.
Figure 2: Bragg spectra throughout the BCS–BEC crossover.
Figure 3: Bragg spectra and pairing gap near unitarity.
Figure 4: Speed of sound across the BCS–BEC crossover.

Similar content being viewed by others

References

  1. Nambu, Y. & Jona-Lasino, G. Dynamical model of elementary particles based on an analogy with superconductivity. Phys. Rev. 122, 345–358 (1961).

    Article  ADS  Google Scholar 

  2. Ashcroft, N. W. & Mermin, N. D. Solid State Physics (Holt, Rinehart & Winston, 1976).

    MATH  Google Scholar 

  3. Griffin, A. Excitations in a Bose Condensed Liquid (Cambridge Univ. Press, 1993).

    Book  Google Scholar 

  4. Anderson, P. W. Random-phase approximation in the theory of superconductivity. Phys. Rev. 112, 1900–1916 (1958).

    Article  ADS  MathSciNet  Google Scholar 

  5. Goldstone, J. Field theories with superconductor solutions. Nuovo Cimento. 19, 154–164 (1961).

    Article  MathSciNet  Google Scholar 

  6. Pekker, D. & Varma, C. M. Amplitude/Higgs modes in condensed matter physics. Annu. Rev. Condens. Matter Phys. 6, 269–297 (2015).

    Article  ADS  Google Scholar 

  7. Bogoliubov, N. N. On the theory of superfluidity. J. Phys. USSR 11, 23–32 (1947).

    MathSciNet  Google Scholar 

  8. Zwerger, W. (ed.) BCS–BEC Crossover and the Unitary Fermi Gas (Lecture Notes in Physics, Springer, 2012).

  9. Joseph, J. et al. Measurement of sound velocity in a Fermi gas near a Feshbach resonance. Phys. Rev. Lett. 98, 170401 (2007).

    Article  ADS  Google Scholar 

  10. Sidorenkov, L. A. et al. Second sound and the superfluid fraction in a Fermi gas with resonant interactions. Nature 498, 78–81 (2013).

    Article  ADS  Google Scholar 

  11. Weimer, W. et al. Critical velocity in the BEC-BCS crossover. Phys. Rev. Lett. 114, 095301 (2015).

    Article  ADS  Google Scholar 

  12. Haussmann, R., Rantner, W., Cerrito, S. & Zwerger, W. Thermodynamics of the BCS–BEC crossover. Phys. Rev. A 75, 023610 (2007).

    Article  ADS  Google Scholar 

  13. Stenger, J. et al. Bragg spectroscopy of a Bose–Einstein condensate. Phys. Rev. Lett. 82, 4569–4573 (1999).

    Article  ADS  Google Scholar 

  14. Steinhauer, J., Ozeri, R., Katz, N. & Davidson, N. Excitation spectrum of a Bose–Einstein condensate. Phys. Rev. Lett. 88, 120407 (2002).

    Article  ADS  Google Scholar 

  15. Veeravalli, G., Kuhnle, E., Dyke, P. & Vale, C. J. Bragg spectroscopy of a strongly interacting Fermi gas. Phys. Rev. Lett. 101, 250403 (2008).

    Article  ADS  Google Scholar 

  16. Rueff, J.-P. & Shukla, A. Inelastic X-ray scattering by electronic excitations under high pressure. Rev. Mod. Phys. 82, 847–896 (2010).

    Article  ADS  Google Scholar 

  17. Brunello, A., Dalfovo, F., Pitaevskii, L., Stringari, S. & Zambelli, F. Momentum transferred to a trapped Bose–Einstein condensate by stimulated light scattering. Phys. Rev. A 64, 063614 (2001).

    Article  ADS  Google Scholar 

  18. Beliaev, S. T. Energy spectrum of a non-ideal Bose gas. Sov. Phys. JETP 2, 299–307 (1958).

    Google Scholar 

  19. Schunck, C. H., Shin, Y., Schirotzek, A. & Ketterle, W. Determination of the fermion pair size in a resonantly interacting superfluid. Nature 454, 739–743 (2008).

    Article  ADS  Google Scholar 

  20. Marini, M., Pistolesi, F. & Strinati, G. C. Evolution from BCS superconductivity to Bose condensation: analytic results for the crossover in three dimensions. Eur. Phys. J. B 1, 151–159 (1998).

    Article  ADS  Google Scholar 

  21. Combescot, R., Kagan, M. Yu. & Stringari, S. Collective mode of homogeneous superfluid Fermi gases in the BEC–BCS crossover. Phys. Rev. A 74, 042717 (2006).

    Article  ADS  Google Scholar 

  22. Hoinka, S., Lingham, M., Delehaye, M. & Vale, C. J. Dynamic spin response of a strongly interacting Fermi gas. Phys. Rev. Lett. 109, 050403 (2012).

    Article  ADS  Google Scholar 

  23. Ku, M. J. H., Sommer, A. T., Cheuk, L. W. & Zwierlein, M. W. Revealing the superfluid lambda transition in the universal thermodynamics of a unitary Fermi gas. Science 335, 563–567 (2012).

    Article  ADS  Google Scholar 

  24. Stewart, J. T., Gaebler, J. P. & Jin, D. S. Using photoemission spectroscopy to probe a strongly interacting Fermi gas. Nature 454, 744–747 (2008).

    Article  ADS  Google Scholar 

  25. Schirotzek, A., Shin, Y., Schunck, C. H. & Ketterle, W. Determination of the superfluid gap in atomic Fermi gases by quasiparticle spectroscopy. Phys. Rev. Lett. 101, 140403 (2008).

    Article  ADS  Google Scholar 

  26. Pieri, P., Pisani, L. & Strinati, G. C. BCS–BEC crossover at finite temperature in the broken-symmetry phase. Phys. Rev. B 70, 094508 (2004).

    Article  ADS  Google Scholar 

  27. Carlson, J. & Reddy, S. Superfluid pairing gap in strong coupling. Phys. Rev. Lett. 100, 150403 (2008).

    Article  ADS  Google Scholar 

  28. Diener, R. B., Sensarma, R. & Randeria, M. Quantum fluctuations in the superfluid state of the BCS–BEC crossover. Phys. Rev. A 77, 023626 (2008).

    Article  ADS  Google Scholar 

  29. Gubler, P., Yamamoto, N., Hatsuda, T. & Nishida, Y. Single-particle spectral density of the unitary Fermi gas: novel approach based on the operator product expansion, sum rules and the maximum entropy method. Ann. Phys. 356, 467–497 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  30. Tajima, H. et al. Strong-coupling corrections to ground-state properties of a superfluid Fermi gas. Phys. Rev. A 95, 043625 (2017).

    Article  ADS  Google Scholar 

  31. Kurkjian, H., Castin, Y. & Sinatra, A. Concavity of the collective excitation branch of a Fermi gas in the BEC–BCS crossover. Phys. Rev. A 93, 013623 (2016).

    Article  ADS  Google Scholar 

  32. Manini, N. & Salasnich, L. Bulk and collective properties of a dilute Fermi gas in the BCS–BEC crossover. Phys. Rev. A 71, 033625 (2005).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank W. Zwerger, G. Strinati, L. Salasnich and Y. Ohashi for sharing their data and comments on the manuscript and P. Hannaford for fruitful discussions. This work was supported by ARC Discovery Project DP130101807. G.M.B. wishes to acknowledge the support of the Villum Foundation via Grant No. VKR023163 and ARC Discovery Project DP160102739.

Author information

Authors and Affiliations

  1. Centre for Quantum and Optical Sciences, Swinburne University of Technology, Melbourne, 3122, Australia

    Sascha Hoinka, Paul Dyke, Marcus G. Lingham & Chris J. Vale

  2. Department of Applied Physics, COMP Centre of Excellence, Aalto University School of Science, FI 00076 Aalto, Finland

    Jami J. Kinnunen

  3. Institut for Fysik og Astronomi, Aarhus Universitet, 8000 Aarhus C, Denmark

    Georg M. Bruun

Authors
  1. Sascha Hoinka
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Paul Dyke
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Marcus G. Lingham
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jami J. Kinnunen
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Georg M. Bruun
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Chris J. Vale
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

S.H., P.D., M.G.L. and C.J.V. conducted the experimental work and data analysis. J.J.K. and G.M.B. performed the theoretical calculations. All authors contributed to the manuscript preparation.

Corresponding author

Correspondence to Chris J. Vale.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 372 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hoinka, S., Dyke, P., Lingham, M. et al. Goldstone mode and pair-breaking excitations in atomic Fermi superfluids. Nature Phys 13, 943–946 (2017). https://doi.org/10.1038/nphys4187

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphys4187

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing