Abstract
Resonant energy transfers, the non-radiative redistribution of an electronic excitation between two particles coupled by the dipole–dipole interaction, lie at the heart of a variety of phenomena1, notably photosynthesis. In 1948, Förster established the theory of fluorescence resonant energy transfer (FRET) between broadband, nearly-resonant donors and acceptors2. The 1/R6 scaling of the energy transfer rate, where R is the distance between particles, enabled widespread use of FRET as a ‘spectroscopic ruler’ for determining nanometric distances in biomolecules3. The underlying mechanism is a coherent dipolar coupling between particles, as recognized in the early days of quantum mechanics4, but this coherence has not been directly observed so far. Here we study, spectroscopically and in the time domain, the coherent, dipolar-induced exchange of excitations between two Rydberg atoms separated by up to 15 μm, and brought into resonance by applying an electric field. Coherent oscillation of the system between two degenerate pair states then occurs at a frequency scaling as 1/R3, the hallmark of resonant dipole–dipole interactions5. Our results not only demonstrate, at the fundamental level of two atoms, the basic mechanism underlying FRET, but also open exciting prospects for active tuning of strong, coherent interactions in quantum many-body systems.
Similar content being viewed by others
Main
The possibility to tune at will coherent interactions in many-body systems by changing external parameters is one of the key tools enabling quantum simulation. For instance, in ultracold quantum gases, such tuning can be achieved by magnetically-induced Feshbach resonances6,7. Rydberg atoms are another promising platform for the quantum simulation of complex many-body problems, owing to the strong interactions associated with their large principal quantum numbers8. They have proved to be an efficient tool for characterizing non-radiative exchange of energy in resonant collisional processes9, studying collective effects10 and engineering quantum states of matter11. The observation of Rydberg blockade between individual atoms12,13, where the strong interaction between Rydberg states inhibits multiple excitations within a blockade sphere, opens the way towards the development of Rydberg quantum simulators14. An appealing tool for those applications is the possibility to tune the strength of the interactions by external electric fields using Förster resonances15,16,17,18,19,20,21,22,23. So far, owing to inhomogeneities in the atomic ensembles used in experiments, only indirect evidence for the coherent character of the interaction has been obtained24,25.
Here, we study a system of two single atoms at a Förster resonance. We first perform a spectroscopic measurement of the energies of the two-atom states as a function of the applied electric field, and observe directly the avoided crossing between pair states induced by the dipole–dipole interaction. The splitting at resonance is observed to scale as 1/R3 as a function of the distance R between the atoms. In a second experiment, we prepare the system in a given pair state away from resonance, and switch to resonance for a controlled time, revealing the coherent oscillation between the two degenerate pair states induced by the dipolar interaction. These results open the way to real-time tuning of interactions for quantum simulation with Rydberg atoms11,14.
Two atoms located at positions R1 and R2 interact through the dipole–dipole interaction

where  is the electric dipole moment of atom i (i = 1,2), R = R2 − R1 and n = R/R. When the two atoms are prepared in the same state,
is the electric dipole moment of atom i (i = 1,2), R = R2 − R1 and n = R/R. When the two atoms are prepared in the same state,  usually has no effect to first order, as the average value of the dipole moment vanishes in an atomic eigenstate. Second-order perturbation theory gives rise to an energy shift of the atom pair, which results in the van der Waals interaction26UvdW ∝ R−6. However, resonance effects between two Rydberg atoms can occur when two pair states are degenerate5, and in this case the dipolar interaction manifests itself at first order. Such a resonance, called a ‘Förster resonance’ in analogy with the FRET mechanism at work in photochemistry, can be achieved using small electric fields to Stark-tune the energy of the pair states.
usually has no effect to first order, as the average value of the dipole moment vanishes in an atomic eigenstate. Second-order perturbation theory gives rise to an energy shift of the atom pair, which results in the van der Waals interaction26UvdW ∝ R−6. However, resonance effects between two Rydberg atoms can occur when two pair states are degenerate5, and in this case the dipolar interaction manifests itself at first order. Such a resonance, called a ‘Förster resonance’ in analogy with the FRET mechanism at work in photochemistry, can be achieved using small electric fields to Stark-tune the energy of the pair states.
In this work, we use the states |p〉 = |61P1/2, mJ = 1/2〉, |d〉 = |59D3/2, mJ = 3/2〉 and |f〉 = |57F5/2, mJ = 5/2〉 of 87Rb. The pair states |dd〉, |pf〉 and |fp〉 are almost degenerate (Fig. 1a): their Förster defect Δ0 = (Epf − Edd)/h, in the absence of an electric field, is only 8.5 MHz (h is Planck’s constant). Using the differential Stark effect between |dd〉 and |pf〉, they can be brought to exact resonance by applying an electric field Fres ≃ 32 mV cm−1 (Fig. 1b). The small electric fields at play ensure that we work in a regime of induced dipoles (even for the highly polarizable f state), as opposed to the rigid dipoles obtained for larger electric fields. At resonance, the eigenstates of the interacting system are  , where
, where  . If the system is initially prepared in |dd〉, it thus oscillates between the two degenerate electronic configurations with a frequency given by the dipolar coupling
. If the system is initially prepared in |dd〉, it thus oscillates between the two degenerate electronic configurations with a frequency given by the dipolar coupling  (where
(where  ). In particular, after half a period of interaction, the system has evolved to the entangled state
). In particular, after half a period of interaction, the system has evolved to the entangled state  .
.
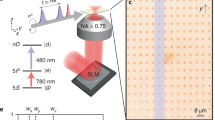
a, The pair states |dd〉 and  are coupled by the dipolar interaction at a Förster resonance. b, Stark effect of the pair states. In the absence of coupling, the two pair-state energy levels (dotted lines) vary when an external electric field F is applied, and cross each other for F = Fres. The coupled system (solid lines) undergoes an avoided crossing at resonance (vertical dashed line). c, Experimental set-up. Two individual 87Rb atoms are trapped in microscopic optical tweezers separated by a distance R. Eight independent electrodes allow the application of a tunable electric field F along the internuclear axis z. d, Structure of the coupled levels at resonance. We scan the excitation laser (blue arrow) to perform a two-atom excitation from |gg〉 to |dd〉 via the intermediate, one-excitation state
are coupled by the dipolar interaction at a Förster resonance. b, Stark effect of the pair states. In the absence of coupling, the two pair-state energy levels (dotted lines) vary when an external electric field F is applied, and cross each other for F = Fres. The coupled system (solid lines) undergoes an avoided crossing at resonance (vertical dashed line). c, Experimental set-up. Two individual 87Rb atoms are trapped in microscopic optical tweezers separated by a distance R. Eight independent electrodes allow the application of a tunable electric field F along the internuclear axis z. d, Structure of the coupled levels at resonance. We scan the excitation laser (blue arrow) to perform a two-atom excitation from |gg〉 to |dd〉 via the intermediate, one-excitation state  . The detuning between the laser frequency and the position of |dd〉 in the absence of interactions (grey horizontal line) is denoted by δ.
. The detuning between the laser frequency and the position of |dd〉 in the absence of interactions (grey horizontal line) is denoted by δ.
Our experimental set-up has been described previously26,27. We trap two single laser-cooled atoms in optical tweezers separated by a controlled distance R of a few micrometres (Fig. 1c). A set of eight independent electrodes allows us to apply a controlled electric field F aligned with the internuclear axis28. A 3 G magnetic field, also aligned along z, is used to split the Zeeman sublevels. We optically pump the atoms in the ground state |g〉 = |5S1/2, F = 2, mF = 2〉 (with an efficiency >90%), which we couple, with an effective Rabi frequency Ω, to the Rydberg state |d〉 using a two-photon transition (using two lasers of wavelengths 795 nm and 474 nm, with π and σ+ polarizations, respectively). The readout of the states of the atoms is performed by shining resonant light at 780 nm on the atoms, giving a fluorescence signal only if the atom is in |g〉 (an atom in a Rydberg state, be it |p〉, |d〉, or |f〉, is lost from the trap during the sequence). Repeating the same sequence ∼100 times allows us to reconstruct the four populations Pgg, Pgr, Prg and Prr (where r stands for any of the Rydberg states p, d and f, which we cannot discriminate directly with our loss-based detection scheme), with a typical uncertainty in the measurement of Pij on the order of ±0.05 (see representative error bars in Figs 2b and 3b).
a, Two-atom excitation spectrum where the population of doubly-Rydberg-excited states, Prr, is plotted as a function of δ and F, showing the avoided crossing between the resonant pair states. The white dashed line indicates the position of the Förster resonance. b, Spectrum Prr(δ) at resonance for R = 8.1 μm. A representative error bar (one standard error in the measurement of Prr) is shown. A double Gaussian (solid line) is fit to the data. c, Double-logarithmic plot of the splitting ΔE between the peaks, at resonance, as a function of R. Error bars are one standard deviation in the determination of ΔE in the fit by a double Gaussian. The solid line shows a fit by a power law, giving an exponent −3.2 ± 0.2.
a, Experimental sequence. After exciting the atoms to |dd〉 (first π-pulse, of duration 200 ns), we switch on the resonant interaction for a variable amount of time T by tuning the electric field to Fres. The system oscillates back and forth between the two pair states |dd〉 and  for the duration T. A deexcitation pulse (second π-pulse) couples back the |dd〉 part of the resulting state to |gg〉. b, Evolution of Pgg as a function of the interaction time for several values of R. Pgg oscillates at a frequency fosc which depends on R. A representative error bar (one standard error in the measurement of Pgg) is shown. The solid lines are fits by a damped sine wave with frequency fosc. c, Double-logarithmic plot of the oscillation frequency fosc as a function of R. Error bars correspond to one standard deviation in the determination of fosc. The solid line shows a fit by a power law, giving an exponent −3.0 ± 0.1.
for the duration T. A deexcitation pulse (second π-pulse) couples back the |dd〉 part of the resulting state to |gg〉. b, Evolution of Pgg as a function of the interaction time for several values of R. Pgg oscillates at a frequency fosc which depends on R. A representative error bar (one standard error in the measurement of Pgg) is shown. The solid lines are fits by a damped sine wave with frequency fosc. c, Double-logarithmic plot of the oscillation frequency fosc as a function of R. Error bars correspond to one standard deviation in the determination of fosc. The solid line shows a fit by a power law, giving an exponent −3.0 ± 0.1.
We first fix R = 8.1 μm and perform a spectroscopic measurement to find the electric field Fres corresponding to the Förster resonance. Our laser system couples |gg〉 to |dd〉 (but not to |pf〉 or |fp〉), via the states |dg〉 and |gd〉. Thus |gg〉 is partially coupled to the states |+〉 and |−〉 at resonance. For increasing values of F, we scan the laser detuning δ (defined with respect to the transition |gg〉 to |dd〉, see Fig. 1d) and measure the probability Prr for both atoms to be in a Rydberg state (Fig. 2a). For F = 0, we observe a single line centred at δ/(2π) ≈ −5 MHz, corresponding to the attractive van der Waals interaction between the two atoms out of resonance. For F ≈ 20 mV cm−1, a repulsive branch appears in the spectrum, a signature of the interaction between |dd〉 and  . Increasing the field even further allows scanning across the avoided crossing until only one peak is visible again. We reach the Förster resonance (smallest splitting between the two peaks) at Fres = 32 ± 4 mV cm−1, where we observe two symmetric peaks corresponding to |±〉. The spectra also show further small structures in addition to the two main peaks. However, to extract the interaction energy in a simple way, we fit the spectra by two Gaussians with a splitting ΔE between the two peaks (Fig. 2b).
. Increasing the field even further allows scanning across the avoided crossing until only one peak is visible again. We reach the Förster resonance (smallest splitting between the two peaks) at Fres = 32 ± 4 mV cm−1, where we observe two symmetric peaks corresponding to |±〉. The spectra also show further small structures in addition to the two main peaks. However, to extract the interaction energy in a simple way, we fit the spectra by two Gaussians with a splitting ΔE between the two peaks (Fig. 2b).
We then measure the evolution of the spectra at resonance when varying the distance R. When R increases, the splitting between the peaks decreases. Figure 2c is a double-logarithmic plot of ΔE versus R. The data show a power-law behaviour of exponent −3.2 ± 0.2, consistent with the expected C3/R3 law. We measure C3 = 2.1 ± 0.1 GHz μm3, where the error is statistical. Systematic effects are an overall ∼5% uncertainty in our calibration of R, a small bias in the determination of ΔE due to the choice of double Gaussian functions to fit the data and possible residual light-shifts in the two-photon spectroscopy. (To estimate the bias introduced by our choice of fit function, we fitted simulated spectra, obtained by solving the optical Bloch equations, by double Gaussians. The extracted splitting underestimates by ≃10% the actual splitting ΔE.) Theoretical calculations29 give C3, th ≃ 2.54 GHz μm3.
We now study the coherence properties of the system at resonance using a sequence (Fig. 3a) reminiscent of pump–probe spectroscopy. We prepare the system in the state |dd〉 using a π-pulse of 200 ns, which transfers each atom from |g〉 to |d〉. To start in a pure |dd〉 state, we perform the excitation in the van der Waals regime above resonance (F ≈ 64 mV cm−1), where the Förster defect is Δ(F) ≥ h × 100 MHz and where interactions are weak. We then turn on the resonant interaction for a variable duration T, by rapidly switching (risetime below 10 ns) the field to Fres. During this time, the two-atom system oscillates between |dd〉 and the entangled state  , with a frequency
, with a frequency  given by the dipolar coupling. We then apply a deexcitation π-pulse identical to the first one to read out the state of the system. The deexcitation pulse couples the |dd〉 component of the system back to |gg〉. At the end of the sequence we measure the probability Pgg to be back in |gg〉, thus indirectly measuring the population left in |dd〉 after the pulse of electric field. We observe highly contrasted oscillations between |dd〉 and
given by the dipolar coupling. We then apply a deexcitation π-pulse identical to the first one to read out the state of the system. The deexcitation pulse couples the |dd〉 component of the system back to |gg〉. At the end of the sequence we measure the probability Pgg to be back in |gg〉, thus indirectly measuring the population left in |dd〉 after the pulse of electric field. We observe highly contrasted oscillations between |dd〉 and  , with a frequency depending on R (Fig. 3b).
, with a frequency depending on R (Fig. 3b).
The oscillations between two states are a direct proof of the coherent nature of the coupling underlying Förster energy transfer, and also allow a more accurate determination of the interaction energy than the spectroscopic method described above. We fit the oscillation by a damped sine wave to extract the oscillation frequency fosc. Figure 3c shows a double-logarithmic plot of the values of fosc as a function of R. The data shows a power-law behaviour of exponent −3.0 ± 0.1, again in excellent agreement with the expected R−3 behaviour. The measured C3 = 2.39 ± 0.03 GHz μm3 is also close to the theoretical value.
The observed damping of the oscillations comes mainly from dephasing, arising from two effects. First, shot-to-shot fluctuations in the distance R (on the order of δR ≃ 170 nm), due to the finite temperature of the atoms in the tweezers, give rise to dephasing, as the oscillation frequency fosc ∝ 1/R3 is slightly different for each realization. This effect dominates at short distances: for instance, for R ≃ 9 μm, the corresponding spread δfosc/fosc = 3δR/R in relative frequencies reaches ∼6%, which is enough to reduce the contrast of the oscillations by more than a factor of two after only four oscillation periods. Second, the voltages applied to the electrodes also fluctuate from shot to shot by a few mV, inducing fluctuations in F and thus in the detuning Δ(F) from resonance (by a fraction of a MHz for our parameters). This has negligible impact for small R, but appreciably contributes to the damping for large R, where the dipolar interaction is weaker. In principle, both sources of damping can be strongly decreased by technical improvements in the set-up, using colder atoms as demonstrated recently 30,31 and more stable voltage sources.
Our results open exciting prospects for real-time tuning of interactions in systems of Rydberg atoms, in particular to switch on and off Ryberg blockade on nanosecond timescales. As an illustration, in the above experiment, when switching F from 64 mV cm−1 (away from resonance) to 32 mV cm−1 (right on resonance), the blockade shift between two atoms separated by R = 10 μm varies from U = UvdW ∼ h × 0.2 MHz (van der Waals regime) up to U = ΔE/2 ∼ h × 4 MHz (C3/R3 regime). If the pair of atoms initially in |gg〉 were driven with a Rabi frequency Ω/(2π) ∼ 1 MHz, one would observe a strong blockade in the second case, whereas blockade would be almost totally suppressed in the first situation. This means that, simply by changing the value of the electric field by a few mV cm−1, we obtain a twenty-fold enhancement of the interaction, and the blockade radius is increased by a factor ∼2 in real time, a feature hard to achieve by other means.
A natural extension of this work will consist in measuring the angular dependence of resonant interactions29, in view of tailoring even further the interactions between two particles. Extending our results beyond two particles, to few-body32 and many-body systems15,16,23, will enable the study of transport of excitations and generation of entanglement in fully controlled many-body systems.
References
Andrews, D. L. & Demidov, A. A. Resonance Energy Transfer (Wiley, 1999).
Förster, T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Ann. Phys. 437, 55–75 (1948).
Stryer, L. & Haugland, R. P. Energy transfer: A spectroscopic ruler. Proc. Natl Acad. Sci. USA 58, 719–726 (1967).
Clegg, R. M. Reviews in Fluorescence 2006 1–45 (Springer, 2006).
Walker, T. G. & Saffman, M. Zeros of Rydberg–Rydberg Föster interactions. J. Phys. B 38, S309–S319 (2005).
Inouye, S. et al. Observation of Feshbach resonances in a Bose–Einstein condensate. Nature 392, 151–154 (1998 ).
Chin, C., Grimm, R., Julienne, P. & Tiesinga, E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 82, 1225–1286 (2010).
Gallagher, T. F. Rydberg Atoms (Cambridge Univ. Press, 2005).
Safinya, K. A., Delpech, J. F., Gounand, F., Sandner, W. & Gallagher, T. F. Resonant Rydberg-atom–Rydberg-atom collisions. Phys. Rev. Lett. 47, 405–408 (1981).
Comparat, D. & Pillet, P. Dipole blockade in a cold Rydberg atomic sample. J. Opt. Soc. Am. B 27, A208–A232 (2010).
Saffman, M., Walker, T. G. & Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 82, 2313–2363 (2010).
Urban, E. et al. Observation of Rydberg blockade between two atoms. Nature Phys. 5, 110–114 (2009).
Gaëtan, A. et al. Observation of collective excitation of two individual atoms in the Rydberg blockade regime. Nature Phys. 5, 115–118 (2009).
Weimer, H., Müller, M., Lesanovsky, I., Zoller, P. & Büchler, H. P. A Rydberg quantum simulator. Nature Phys. 6, 382–388 (2010).
Anderson, W. R., Veale, J. R. & Gallagher, T. F. Resonant dipole–dipole energy transfer in a nearly frozen Rydberg gas. Phys. Rev. Lett. 80, 249–252 (1998).
Mourachko, I. et al. Many-body effects in a frozen Rydberg gas. Phys. Rev. Lett. 80, 253–256 (1998).
Anderson, W. R., Robinson, M. P., Martin, J. D. D. & Gallagher, T. F. Dephasing of resonant energy transfer in a cold Rydberg gas. Phys. Rev. A 65, 063404 (2002).
Mudrich, M., Zahzam, N., Vogt, T., Comparat, D. & Pillet, P. Back and forth transfer and coherent coupling in a cold Rydberg dipole gas. Phys. Rev. Lett. 95, 233002 (2005).
Vogt, T. et al. Electric-field induced dipole blockade with Rydberg atoms. Phys. Rev. Lett. 99, 073002 (2007).
Reinhard, A., Younge, K. C. & Raithel, G. Effect of Förster resonances on the excitation statistics of many-body Rydberg systems. Phys. Rev. A 78, 060702(R) (2008).
Van Ditzhuijzen, C. S. E. et al. Spatially resolved observation of dipole–dipole interaction between Rydberg atoms. Phys. Rev. Lett. 100, 243201 (2008).
Ryabtsev, I. I., Tretyakov, D. B., Beterov, I. I. & Entin, V. M. Observation of the Stark-tuned Förster resonance between two Rydberg atoms. Phys. Rev. Lett. 104, 073003 (2010).
Günter, G. et al. Observing the dynamics of dipole-mediated energy transport by interaction-enhanced imaging. Science 342, 954–956 (2013).
Nipper, J. et al. Highly resolved measurements of Stark-tuned Förster resonances between Rydberg atoms. Phys. Rev. Lett. 108, 113001 (2012).
Nipper, J. et al. Atomic pair-state interferometer: Controlling and measuring an interaction-induced phase shift in Rydberg-atom pairs. Phys. Rev. X 2, 031011 (2012).
Béguin, L., Vernier, A., Chicireanu, R., Lahaye, T. & Browaeys, A. Direct measurement of the van der Waals interaction between two Rydberg atoms. Phys. Rev. Lett. 110, 263201 (2013).
Nogrette, F. et al. Single-atom trapping in holographic 2D arrays of microtraps with arbitrary geometries. Phys. Rev. X 4, 021034 (2014).
Löw, R. et al. An experimental and theoretical guide to strongly interacting Rydberg gases. J. Phys. B 45, 113001 (2012).
Reinhard, A., Cubel Liebisch, T., Knuffman, B. & Raithel, G. Level shifts of rubidium Rydberg states due to binary interactions. Phys. Rev. A 75, 032712 (2007).
Kaufman, A. M., Lester, B. J. & Regal, C. A. Cooling a single atom in an optical tweezer to its quantum ground state. Phys. Rev. X 2, 041014 (2012).
Thompson, J. D., Tiecke, T. G., Zibrov, A. S., Vuletić, V. & Lukin, M. D. Coherence and Raman sideband cooling of a single atom in an optical tweezer. Phys. Rev. Lett. 110, 133001 (2013).
Gurian, J. H. et al. Observation of a resonant four-body interaction in cold cesium Rydberg atoms. Phys. Rev. Lett. 108, 023005 (2012).
Acknowledgements
We thank C. S. Adams for enlightening discussions, F. Nogrette for technical assistance and M. Besbes for finite-element calculations of the electric field configuration. This work was supported financially by the EU (ERC Stg Grant ARENA, FET-Open Xtrack project HAIRS, EU Marie-Curie program ITN COHERENCE FP7-PEOPLE-2010-ITN-265031 (H.L.)), by the DGA (L.B.), and by Région Île-de-France (LUMAT and Triangle de la Physique, LAGON project).
Author information
Authors and Affiliations
Contributions
All authors contributed extensively to the work presented in this paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Ravets, S., Labuhn, H., Barredo, D. et al. Coherent dipole–dipole coupling between two single Rydberg atoms at an electrically-tuned Förster resonance. Nature Phys 10, 914–917 (2014). https://doi.org/10.1038/nphys3119
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3119
This article is cited by
-
Quantum computing with Rydberg atom graphs
Journal of the Korean Physical Society (2023)
-
Optical van-der-Waals forces in molecules: from electronic Bethe-Salpeter calculations to the many-body dispersion model
Nature Communications (2022)
-
Ultrafast energy exchange between two single Rydberg atoms on a nanosecond timescale
Nature Photonics (2022)
-
Optimized nonadiabatic holonomic quantum computation based on Förster resonance in Rydberg atoms
Frontiers of Physics (2022)
-
Energy funnelling within multichromophore architectures monitored with subnanometre resolution
Nature Chemistry (2021)