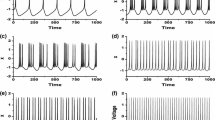
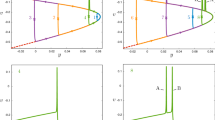
Abstract
Many neural systems display adaptive properties that occur on timescales that are slower than the time scales associated withrepetitive firing of action potentials or bursting oscillations. Spike frequency adaptation is the name givento processes thatreduce the frequency of rhythmic tonic firing of action potentials,sometimes leading to the termination of spiking and the cell becomingquiescent. This article examines these processes mathematically,within the context of singularly perturbed dynamical systems.We place emphasis on the lengths of successive interspikeintervals during adaptation. Two different bifurcation mechanisms insingularly perturbed systems that correspond to the termination offiring are distinguished by the rate at which interspike intervalsslow near the termination of firing. We compare theoreticalpredictions to measurement of spike frequency adaptation in a modelof the LP cell of the lobster stomatogastric ganglion.
Similar content being viewed by others
References
Arnold VI, Afrajmovich VS, Ilyashenko YS, Shilnikov LP (1994) Dynamical Systems V. Springer-Verlag.
Belyakov LA(1974) A case of the generation of periodic motion with homoclinic curves. Math. Notes of the Acad. Sci. USSR15:336–341.
Bertram R, Butte MJ, Kiemel T, Sherman A (1995) Topological and phenomenological classification of bursting oscillations. Bull. Math. Biology57:413–449.
Bosch M, Simo C (1993) Attractors in a Silnikov-Hopf scenario and a related one dimensional map. Phys. D62:217–229.
Buchholtz F, Golowasch J, Epstein I, Marder E (1992) Mathematical model of an identified stomatogastric ganglion neuron. J. Neurophysiol. 67:332–339.
Deng B, Sakamoto K (1995) Silnikov-Hopf bifurcations. J. Diff. Eq. 119:1–23.
Ermentrout B, Kopell N (1986) Parabolic bursting in an excitable system coupled with a slowoscillation. Siam J. App. Math46:233–253.
Fenichel N (1971) Persistence and smoothness of invariant manifolds for flows. Indiana Univ. Math. J.21:193–226.
Flamm RE, Harris-Warrick RM (1986) Aminergic modulation in the lobster stomatogastric ganglion. J. Neurophysiol.55:847–881.
Glendinning P, Sparrow C (1984) Local and global behavior near homoclinic orbits. J. Statist. Phys.34:645–696.
Golowasch JP (1991) Characterization of a stomatogastric ganglion neuron: A biophysical and mathematical interpretation. Thesis, Brandeis University.
Guckenheimer J, Holmes P (1983) Nonlinear Oscillations, Dynamical Systems, and Bifurcation of Vector Fields. Springer Verlag.
Harris-Warrick R, Coniglio L, Levini R, Gueron S, Guckenheimer J (1995) Dopamine modulation of two subthreshold currents produces phase shifts in activity of an identified neuron. J. Neurophysiol. 74:1404–1420.
Hartline D, Graubard K(1992) Cellular and synaptic properties in the crustacean stomatogastric nervous system. In: R Harris-Warrick, E Marder, A Selverston, M Moulins, eds. Dynamic Biological Networks. MIT Press, Cambridge, MA. pp. 31–86.
Hille B (1992) Ionic Channels of Excitable Membranes. Sinauer. Hirschberg P, Knobloch E (1993) Silnikov-Hopf bifurcation. Phys.D 62:202–216.
Ilyashenko YS, Yakovenko SY(1991) Finitely-smooth normal forms of local families of diffeomorphisms and vector fields. Russian Math Surveys46:1–43.
Mishchenko EF, Rozov NK (1980) Differential equations with a small parameter multiplying the highest derivative and relaxation oscillations. Plenum Press.
Nejshtadt AI (1985) Asymptotic investigation of the loss of stability as a pair of eigenvalues slowly cross the imaginary axis. Usp. Mat. Nauk40:190–191.
Newhouse S (1979) The abundance of wild hyperbolic sets and non-smooth stable sets for diffeomorphisms. Publ. Math. I.H.E.S. 50:101–151.
Rinzel J (1987) A formal classification of bursting mechanisms in excitable systems. In: AM Gleason, ed. Proceedings of the International Congress of Mathematicians. American Mathematics Society, pp. 1578–1594.
Rinzel J, Troy W (1982)Bursting phenomena in a simplified Oregonator flow model. J. Chem. Phys.76:1775–1789.
Rinzel J, Ermentrout B (1989) Analysis of neural excitability and oscillations. In: C Koch, I Segev, eds. Methods of Neural Modeling: From Synapses to Networks. MIT Press, Cambridge, MA. pp. 135–169.
Selverston AI, Russell DF, Miller JP, King DG (1976) The stomatogastric nervous system: Structure and function of a small neural network. Prog. Neurobiol.7:215–290.
Shilnikov L, Turaev D (1995)On blue sky catastrophes. Doklady Academii Nauk342:596–599.
Wang X-J, Rinzel J (1995) Oscillatory and bursting properties of neurons. In: M Arbib, ed. The Handbook of Brain Theory and Neural Networks.MIT Press, Cambridge, MA. pp. 686–691.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Guckenheimer, J., Harris-Warrick, R., Peck, J. et al. Bifurcation, Bursting, and Spike Frequency Adaptation. J Comput Neurosci 4, 257–277 (1997). https://doi.org/10.1023/A:1008871803040
Issue Date:
DOI: https://doi.org/10.1023/A:1008871803040