Abstract
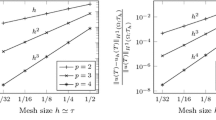
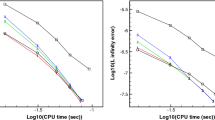
In this paper we construct several numerical approximations for first order Hamilton–Jacobi equations on triangular meshes. We show that, thanks to a filtering procedure, the high order versions are non-oscillatory in the sense of satisfying the maximum principle. The methods are based on the first order Lax–Friedrichs scheme [2] which is improved here adjusting the dissipation term. The resulting first order scheme is ε-monotonic (we explain the expression in the paper) and converges to the viscosity solution as \(\mathcal{O}(\sqrt {\Delta t} )\) for the L ∞-norm. The first high order method is directly inspired by the ENO philosophy in the sense where we use the monotonic Lax–Friedrichs Hamiltonian to reconstruct our numerical solutions. The second high order method combines a spatial high order discretization with the classical high order Runge–Kutta algorithm for the time discretization. Numerical experiments are performed for general Hamiltonians and L 1, L 2 and L ∞-errors with convergence rates calculated in one and two space dimensions show the k-th order rate when piecewise polynomial of degree k functions are used, measured in L 1-norm.
Similar content being viewed by others
REFERENCES
Abgrall, R. Numerical discretization of boundary conditions for Hamilton-Jacobi equations. SIAM J. Numer. Anal., preprint.
Abgrall, R. (1996). Numerical discretization of first-order Hamilton-Jacobi equations on triangular meshes. Comm. Pure Appl. Math., pp. 1339–1373.
Augoula, S. (2000). Simulation du suivi d'un front de flamme dans un milieu strie- homogénéisé en gé omé trie complexe, Ph.D. thesis, Université de Bordeaux 1.
Augoula, S., and Abgrall, R. High resolution for first-order Hamilton-Jacobi equations on triangular meshes. Numer. Math., submitted.
Augoula, S., and Abgrall, R. (1999). A discontinuous projection algorithm for Hamilton-Jacobi equations. LNCSE Spring Verlag 11.
G. Barles. (1994). Solutions de viscosité des é quations de Hamilton-Jacobi. In Mathé mati-ques et Applications, Vol. 17, Springer-Verlag.
Barles, G., and Souganidis, P. (1991). Convergence of approximation schemes for fully nonlinear second order equations. Asymptotic Analysis, pp. 271–283.
Barth, T. J., and Sethian, J. A. (1998). Numerical schemes for the Hamilton-Jacobi and level set equations on triangulated domains. J. Comput. Phys. 1(145), 1–40.
Benamou, J.-D. (1999). Direct computation of multivalued phase space solutions for Hamilton-Jacobi equations. Comm. Pure Appl. Math., pp. 1443–1475.
Chi-Tien Lin, and Tadmor, E. (2000). High-resolution non-oscillatory central schemes for Hamilton-Jacobi equations. SIAM J. Sci. Comp. 21, 2163–2186.
Ciarlet, P., and Raviart, P. (1972). General Lagrange and Hermite interpolation in Rn with applications to finite element methods. Arch. Rational Mech. and Anal. 46.
Cockburn, B., and Shu, C. (1989). TVB Runge-Kutta local projection discontinuous Galerkin finite element method for scalar conservation laws. II. General framework. Math. Comp. 52, 411–435.
Crandall, M., and Lions, P. (1983). Viscosity solution of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 277(1).
Crandall, M., and Lions, P. (1984). Two approximations of solutions of Hamilton-Jacobi equations. Math. Comp. 43, 1–49.
Crandall, M., Evans, L., and Lions, P. (1984). Some properties of viscosity solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 282(2).
Harten, A., and Osher, S. (1987). Uniformly high order accurate non-oscillatory schemes, I. SIAM J. Numer. Anal. 24, 279–309.
Harten, A., Engquist, B., Osher, S., and Chakravarthy, S. (1987). Uniformly high order accurate essentially non-oscillatory scheme, III. J. Comput. Phys. 71.
Hu, C., and Shu, C. (1999). A discontinuous Galerkin scheme for Hamilton-Jacobi equa-tions. SIAM J. Sci. Comp. 21, 666–690.
Jiang, G., and Peng, D. (2000). Weighted ENO schemes for Hamilton-Jacobi equations. SIAM J. Sci. Comp. 21, 2126–2143.
Le Breton, P., Ribé reau, D., Godfroy, F., Abgrall, R., and Augoula, S. (1998). SRM ballistic analysis by coupling bidimensionnal surface burnback and pressure field com-putations. AIAA 98–3968.
Lin, C.-T., and Tadmor, E.(2000). L1 stability and error estimates for Hamilton-Jacobi equations. Numer. Math., to appear.
Lions, P., and Souganidis, P. (1995). Convergence of MUSCL and filtered schemes for scalar conservation laws and Hamilton-Jacobi equations. Numer. Math. 69, 441–470.
Osher, S., and Shu, C. (1991). High-order essentially non-oscillatory schemes for Hamilton-Jacobi equations. SIAM J. Numer. Anal. 28(4).
Rouy, E., and Tourin, A. (1992). A viscosity solution approach to shape-from-shading. SIAM J. Numer. Anal. 29(3), 867–884.
Sethian, J. A. (1990). Numerical algorithms for propagating interfaces: Hamilton-Jacobi equations and conservation laws. J. Differential Geom. 1(31), 131–161.
Shi Jin and Zhouping Xin. (1998). Numerical passage from systems of conservation laws to Hamilton-Jacobi equations. SIAM J. Numer. Anal. 35, 2385–2404.
Shu, C., and Osher, S. (1988). Efficient implementation of Essentially Non-oscillatory shock-capturing scheme. J. Comput. Phys.
Souganidis, P. (1985). Approximation schemes for viscosity solution of Hamilton-Jacobi equations. J. Differential Equations 59, 1–43.
Rights and permissions
About this article
Cite this article
Augoula, S., Abgrall, R. High Order Numerical Discretization for Hamilton–Jacobi Equations on Triangular Meshes. Journal of Scientific Computing 15, 197–229 (2000). https://doi.org/10.1023/A:1007633810484
Issue Date:
DOI: https://doi.org/10.1023/A:1007633810484