Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-18T23:06:24.710Z Has data issue: false hasContentIssue false
  • English
  • Français

INITIAL SEGMENTS OF THE DEGREES OF CEERS

Part of: Computability and recursion theory

Published online by Cambridge University Press:  18 February 2022

URI ANDREWS  and
ANDREA SORBI
URI ANDREWS
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN–MADISONMADISON, WI53706-1388, USAE-mail:andrews@math.wisc.eduURL:http://www.math.wisc.edu/~andrews/
ANDREA SORBI
Affiliation:
DEPARTMENT OF INFORMATION ENGINEERING AND MATHEMATICS UNIVERSITY OF SIENA53100SIENA, ITALYE-mail:andrea.sorbi@unisi.itURL:http://www3.diism.unisi.it/~sorbi/
Get access Rights & Permissions [Opens in a new window]

Abstract

It is known that every non-universal self-full degree in the structure of the degrees of computably enumerable equivalence relations (ceers) under computable reducibility has exactly one strong minimal cover. This leaves little room for embedding wide partial orders as initial segments using self-full degrees. We show that considerably more can be done by staying entirely inside the collection of non-self-full degrees. We show that the poset 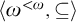can be embedded as an initial segment of the degrees of ceers with infinitely many classes. A further refinement of the proof shows that one can also embed the free distributive lattice generated by the lower semilattice 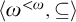as an initial segment of the degrees of ceers with infinitely many classes.

Keywords

initial segmentcomputably enumerable equivalence relationceerdistributive lattice

MSC classification

Primary: 03D30: Other degrees and reducibilities
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 3 , September 2022 , pp. 1260 - 1282
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, U. and Badaev, S., On isomorphism classes of computably enumerable equivalence relations, this Journal, vol. 85 (2020), no. 1, pp. 61–86.Google Scholar
Andrews, U., Badaev, S., and Sorbi, A., A survey on universal computably enumerable equivalence relations , Computability and Complexity. Essays Dedicated to Rodney G. Downey on the Occasion of His 60th Birthday (Day, A., Fellows, M., Greenberg, N., Khoussainov, B., Melnikov, A., and Rosamond, F., editors), Springer, Cham, 2017, pp. 418–451.CrossRefGoogle Scholar
Andrews, U., Lempp, S., Miller, J. S., Ng, K. M., San Mauro, L., and Sorbi, A., Universal computably enumerable equivalence relations, this Journal, vol. 79 (2014), no. 1, pp. 60–88.Google Scholar
Andrews, U., Schweber, N., and Sorbi, A., The theory of ceers computes true arithmetic . Annals of Pure and Applied Logic, vol. 171 (2020), no. 8, p. 102811.CrossRefGoogle Scholar
Andrews, U. and Sorbi, A., Joins and meets in the structure of ceers . Computability, vol. 8 (2019), nos. 3–4, pp. 193–241.CrossRefGoogle Scholar
Balbes, R. and Dwinger, P., Distributive Lattices, University of Missouri Press, Columbia, 1974.Google Scholar
Bernardi, C. and Sorbi, A., Classifying positive equivalence relations, this Journal, vol. 48 (1983), no. 3, pp. 529–538.Google Scholar
Fokina, E., Khoussainov, B., Semukhin, P., and Turetsky, D., Linear orders realized by c.e. equivalence relations, this Journal, vol. 81 (2016), no. 2, pp. 463–482.Google Scholar
Gao, S. and Gerdes, P., Computably enumerable equivalence relations . Studia Logica, vol. 67 (2001), no. 1, pp. 27–59.CrossRefGoogle Scholar
Gavruskin, A., Jain, S., Khoussainov, B., and Stephan, F., Graphs realised by r.e. equivalence relations . Annals of Pure and Applied Logic, vol. 165 (2014), nos. 7–8, pp. 1263–1290.CrossRefGoogle Scholar
Gavryushkin, A., Khoussainov, B., and Stephan, F., Reducibilities among equivalence relations induced by recursively enumerable structures . Theoretical Computer Science, vol. 612 (2016), pp. 137–152.CrossRefGoogle Scholar
Khoussainov, B.. A journey to computably enumerable structures (tutorial lectures). Sailing Routes in the World of Computation: Proceedings of the 14th Conference on Computability in Europe, CiE 2018 (Manea, F., Miller, R. G., and Nowotka, D., editors), Lecture Notes in Computer Science, vol. 10936, Springer, Cham, 2018, pp. 1–19.CrossRefGoogle Scholar
Lachlan, A. H., Initial segments of one–one degrees . Pacific Journal of Mathematics, vol. 29 (1969), pp. 351–366.CrossRefGoogle Scholar
Lachlan, A. H., Two theorems on many-one degrees of recursively enumerable sets . Algebra and Logic, vol. 11 (1972), no. 2, pp. 216–229 (English translation).Google Scholar
Miller, C. F. III, On Group-Theoretic Decision Problems and Their Classification, Annals of Mathematics Studies, vol. 68, Princeton University Press, Princeton, 1971.Google Scholar
Rogers, H. Jr., Theory of Recursive Functions and Effective Computability, McGraw-Hill, New York, 1967.Google Scholar
Soare, R. I., Recursively Enumerable Sets and Degrees, Perspectives in Mathematical Logic, Omega Series, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar