Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-05-31T23:59:56.556Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of free surface on submerged stratified shear instabilities

Published online by Cambridge University Press:  19 March 2018

Mihir H. Shete  and
Anirban Guha Open the ORCID record for Anirban Guha [Opens in a new window]
Mihir H. Shete
Affiliation:
Environmental and Geophysical Fluids Group, Department of Mechanical Engineering, Indian Institute of Technology, Kanpur, Uttar Pradesh 208016, India
Anirban Guha*
Affiliation:
Environmental and Geophysical Fluids Group, Department of Mechanical Engineering, Indian Institute of Technology, Kanpur, Uttar Pradesh 208016, India
*
†Email address for correspondence: anirbanguha.ubc@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we have considered the effects of the shallowness of the domain as well as the air–water free surface on the stratified shear instabilities of the fluid underneath. First, we numerically solve the non-Boussinesq Taylor–Goldstein equation for smooth velocity and density profiles of a model shear layer with a free surface. When the depth of the fluid is relatively shallow compared to the shear layer thickness, the surface gravity waves existing at the free surface come closer to the waves existing in the shear layer. This can lead to resonant wave interactions, making the flow unstable to more varieties of modal instabilities. In order to obtain a deeper understanding of the instability mechanisms, we have performed analytical studies with broken-line profiles (profiles for which vorticity and density are piecewise constant). Furthermore, reduced-order broken-line profiles have also been developed, based on which dispersion diagrams are constructed. Through these diagrams we have underpinned the resonantly interacting waves leading to each type of instability. Two new instabilities have been found; one of them, referred to as the ‘surface gravity – interfacial gravity (SG-IG) mode’, arises due to the interaction between a surface gravity wave and an interfacial gravity wave, and would therefore be absent if there is no internal density stratification. The other one – the ‘surface gravity – lower vorticity (SG-LV) mode’, which arises due to the interaction between a surface gravity wave and the lower vorticity wave, surpasses Kelvin–Helmholtz (KH) instability to become the most unstable mode, provided the system is significantly shallow. Stability boundary of the SG-LV mode is found to be quite different from that of KH. In fact, KH becomes negligible for relatively shallow flows, while SG-LV’s growth rate is significant – comparable to the growth rate of KH for unbounded domains (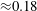${\approx}0.18$). Moreover, the SG-LV mode is found to be analogous to the barotropic mode observed in two-layer quiescent flows. We have found that the effect of a free surface on the Holmboe instability is not appreciable. Holmboe in the presence of a free surface is found to be analogous to the baroclinic mode observed in two-layer quiescent flows. Except for the Holmboe instability, remarkable differences are observed in all other instabilities occurring in shallow domains when the air–water interface is replaced by a rigid lid. We infer that the rigid-lid approximation is valid for large vertical domains and should be applied with caution otherwise. Furthermore, we have also shown that if shear is absent at the free surface, our problem can be modelled using Boussinesq approximation, that is, 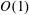$O(1)$ density variations in the inertial terms can still be neglected.

JFM classification

Wakes/Jets: Shear layers Geophysical and Geological Flows: Stratified flows Waves/Free-surface Flows: Surface gravity waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 98 - 125
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: College of Earth, Ocean, and Atmospheric Sciences, Oregon State University, Corvallis, OR 97331, USA.

References

Alexakis, A. 2005 On Holmboe’s instability for smooth shear and density profiles. Phys. Fluids 17 (8), 084103.Google Scholar
Baines, P. G. & Mitsudera, H. 1994 On the mechanism of shear flow instabilities. J. Fluid Mech. 276, 327–342.Google Scholar
Bakas, N. A. & Ioannou, P. J. 2009 Modal and nonmodal growths of inviscid planar perturbations in shear flows with a free surface. Phys. Fluids 21 (2), 024102.Google Scholar
Barros, R. & Choi, W. 2011 Holmboe instability in non-Boussinesq fluids. Phys. Fluids 23 (12), 124103.Google Scholar
Barros, R. & Choi, W. 2014 Elementary stratified flows with stability at low Richardson number. Phys. Fluids 26 (12), 124107.Google Scholar
Carpenter, J. R., Balmforth, N. J. & Lawrence, G. A. 2010 Identifying unstable modes in stratified shear layers. Phys. Fluids 22 (5), 054104.Google Scholar
Carpenter, J. R., Guha, A. & Heifetz, E. 2017 A physical interpretation of the wind-wave instability as interacting waves. J. Phys. Oceanogr. 47 (6), 1441–1455.Google Scholar
Carpenter, J. R., Lawrence, G. A. & Smyth, W. D. 2007 Evolution and mixing of asymmetric Holmboe instabilities. J. Fluid Mech. 582, 103–132.Google Scholar
Carpenter, J. R., Tedford, E. W., Heifetz, E. & Lawrence, G. A. 2013 Instability in stratified shear flow: review of a physical interpretation based on interacting waves. Appl. Mech. Rev. 64 (6), 060801.Google Scholar
Caulfield, C.-C. P. 1994 Multiple linear instability of layered stratified shear flow. J. Fluid Mech. 258, 255–285.Google Scholar
Craik, A. D. D. 1988 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Ehrnström, M. & Villari, G. 2008 Linear water waves with vorticity: rotational features and particle paths. J. Differ. Equ. 244 (8), 1888–1909.Google Scholar
Guha, A. & Lawrence, G. A. 2014 A wave interaction approach to studying non-modal homogeneous and stratified shear instabilities. J. Fluid Mech. 755, 336–364.Google Scholar
Guha, A., Rahmani, M. & Lawrence, G. A. 2013 Evolution of a barotropic shear layer into elliptical vortices. Phys. Rev. E 87 (1), 013020.Google Scholar
Haigh, S. P. & Lawrence, G. A. 1999 Symmetric and nonsymmetric Holmboe instabilities in an inviscid flow. Phys. Fluids 11 (6), 1459–1468.Google Scholar
Hazel, P. 1972 Numerical studies of the stability of inviscid stratified shear flows. J. Fluid Mech. 51 (1), 39–61.Google Scholar
Heifetz, E., Bishop, C. H. & Alpert, P. 1999 Counter-propagating Rossby waves in the barotropic Rayleigh model of shear instability. Q. J. R. Meteorol. Soc. 125 (560), 2835–2853.Google Scholar
Heifetz, E. & Mak, J. 2015 Stratified shear flow instabilities in the non-Boussinesq regime. Phys. Fluids 27 (8), 086601.Google Scholar
Heifetz, E. & Methven, J. 2005 Relating optimal growth to counterpropagating Rossby waves in shear instability. Phys. Fluids 17 (6), 064107.Google Scholar
Holmboe, J. 1962 On the behavior of symmetric waves in stratified shear layers. Geophys. Publ. 24, 67–113.Google Scholar
Kundu, P. K., Cohen, I. M. & Dowling, D. R. 2012 Chapter 7: Gravity waves. In Fluid Mechanics, 5th edn, pp. 253–307. Academic Press.Google Scholar
Lawrence, G. A., Browand, F. K. & Redekopp, L. G. 1991 The stability of a sheared density interface. Phys. Fluids 3, 2360–2370.Google Scholar
Longuet-Higgins, M. S. 1998 Instabilities of a horizontal shear flow with a free surface. J. Fluid Mech. 364, 147–162.Google Scholar
Miles, J. W. 1957 On the generation of surface waves by shear flows. J. Fluid Mech. 3 (2), 185–204.Google Scholar
Rahmani, M., Lawrence, G. A. & Seymour, B. R. 2014 The effect of Reynolds number on mixing in Kelvin–Helmholtz billows. J. Fluid Mech. 759, 612–641.Google Scholar
Sakai, S. 1989 Rossby–Kelvin instability: a new type of ageostrophic instability caused by a resonance between Rossby waves and gravity waves. J. Fluid Mech. 202, 149–176.Google Scholar
Smyth, W. D., Carpenter, J. R. & Lawrence, G. A. 2007 Mixing in symmetric Holmboe waves. J. Phys. Oceanogr. 37 (6), 1566–1583.Google Scholar
Smyth, W. D., Klaassen, G. P. & Peltier, W. R. 1988 Finite amplitude Holmboe waves. Geophys. Astrophys. Fluid 43 (2), 181–222.Google Scholar
Smyth, W. D., Moum, J. N. & Nash, J. D. 2011 Narrowband oscillations in the upper equatorial ocean. Part II. Properties of shear instabilities. J. Phys. Oceanogr. 41 (3), 412–428.Google Scholar
Smyth, W. D. & Peltier, W. R. 1989 The transition between Kelvin–Helmholtz and Holmboe instability: an investigation of the overreflection hypothesis. J. Atmos. Sci. 46 (24), 3698–3720.Google Scholar
Smyth, W. D. & Peltier, W. R. 1991 Instability and transition in finite-amplitude Kelvin–Helmholtz and Holmboe waves. J. Fluid Mech. 228, 387–415.Google Scholar
Sutherland, B. R. 2010 Internal Gravity Waves. Cambridge University Press.Google Scholar
Sutherland, B. R. & Peltier, W. R. 1992 The stability of stratified jets. Geophys. Astrophys. Fluid 66 (1–4), 101–131.Google Scholar
Turner, J. S. 1979 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Yoshida, S., Ohtani, M., Nishida, S. & Linden, P. F. 1998 Mixing processes in a highly stratified river. In Physical Processes in Lakes and Oceans (ed. Imberger, J.), pp. 389–400. American Geophysical Union.Google Scholar