Article contents
HIGHER ORDER DIFFERENTIABILITY OF OPERATOR FUNCTIONS IN SCHATTEN NORMS
Published online by Cambridge University Press: 13 February 2019
Abstract
We establish the following results on higher order 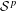 ${\mathcal{S}}^{p}$-differentiability,
${\mathcal{S}}^{p}$-differentiability, 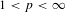 $1<p<\infty$, of the operator function arising from a continuous scalar function
$1<p<\infty$, of the operator function arising from a continuous scalar function 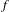 $f$ and self-adjoint operators defined on a fixed separable Hilbert space:
$f$ and self-adjoint operators defined on a fixed separable Hilbert space:
(i)
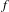 $f$ is
$f$ is  $n$ times continuously Fréchet
$n$ times continuously Fréchet 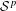 ${\mathcal{S}}^{p}$-differentiable at every bounded self-adjoint operator if and only if
${\mathcal{S}}^{p}$-differentiable at every bounded self-adjoint operator if and only if 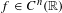 $f\in C^{n}(\mathbb{R})$;
$f\in C^{n}(\mathbb{R})$;(ii) if
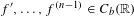 $f^{\prime },\ldots ,f^{(n-1)}\in C_{b}(\mathbb{R})$ and
$f^{\prime },\ldots ,f^{(n-1)}\in C_{b}(\mathbb{R})$ and 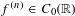 $f^{(n)}\in C_{0}(\mathbb{R})$, then
$f^{(n)}\in C_{0}(\mathbb{R})$, then 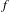 $f$ is
$f$ is  $n$ times continuously Fréchet
$n$ times continuously Fréchet 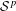 ${\mathcal{S}}^{p}$-differentiable at every self-adjoint operator;
${\mathcal{S}}^{p}$-differentiable at every self-adjoint operator;(iii) if
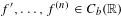 $f^{\prime },\ldots ,f^{(n)}\in C_{b}(\mathbb{R})$, then
$f^{\prime },\ldots ,f^{(n)}\in C_{b}(\mathbb{R})$, then 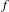 $f$ is
$f$ is  $n-1$ times continuously Fréchet
$n-1$ times continuously Fréchet 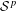 ${\mathcal{S}}^{p}$-differentiable and
${\mathcal{S}}^{p}$-differentiable and  $n$ times Gâteaux
$n$ times Gâteaux 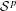 ${\mathcal{S}}^{p}$-differentiable at every self-adjoint operator.
${\mathcal{S}}^{p}$-differentiable at every self-adjoint operator.
We also prove that if 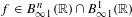 $f\in B_{\infty 1}^{n}(\mathbb{R})\cap B_{\infty 1}^{1}(\mathbb{R})$, then
$f\in B_{\infty 1}^{n}(\mathbb{R})\cap B_{\infty 1}^{1}(\mathbb{R})$, then 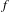 $f$ is
$f$ is  $n$ times continuously Fréchet
$n$ times continuously Fréchet 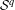 ${\mathcal{S}}^{q}$-differentiable,
${\mathcal{S}}^{q}$-differentiable, 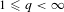 $1\leqslant q<\infty$, at every self-adjoint operator. These results generalize and extend analogous results of Kissin et al. (Proc. Lond. Math. Soc. (3)108(3) (2014), 327–349) to arbitrary
$1\leqslant q<\infty$, at every self-adjoint operator. These results generalize and extend analogous results of Kissin et al. (Proc. Lond. Math. Soc. (3)108(3) (2014), 327–349) to arbitrary  $n$ and unbounded operators as well as substantially extend the results of Azamov et al. (Canad. J. Math.61(2) (2009), 241–263); Coine et al. (J. Funct. Anal.; doi:10.1016/j.jfa.2018.09.005); Peller (J. Funct. Anal.233(2) (2006), 515–544) on higher order
$n$ and unbounded operators as well as substantially extend the results of Azamov et al. (Canad. J. Math.61(2) (2009), 241–263); Coine et al. (J. Funct. Anal.; doi:10.1016/j.jfa.2018.09.005); Peller (J. Funct. Anal.233(2) (2006), 515–544) on higher order 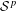 ${\mathcal{S}}^{p}$-differentiability of
${\mathcal{S}}^{p}$-differentiability of 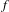 $f$ in a certain Wiener class, Gâteaux
$f$ in a certain Wiener class, Gâteaux 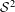 ${\mathcal{S}}^{2}$-differentiability of
${\mathcal{S}}^{2}$-differentiability of 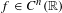 $f\in C^{n}(\mathbb{R})$ with
$f\in C^{n}(\mathbb{R})$ with 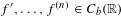 $f^{\prime },\ldots ,f^{(n)}\in C_{b}(\mathbb{R})$, and Gâteaux
$f^{\prime },\ldots ,f^{(n)}\in C_{b}(\mathbb{R})$, and Gâteaux 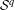 ${\mathcal{S}}^{q}$-differentiability of
${\mathcal{S}}^{q}$-differentiability of 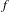 $f$ in the intersection of the Besov classes
$f$ in the intersection of the Besov classes 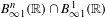 $B_{\infty 1}^{n}(\mathbb{R})\cap B_{\infty 1}^{1}(\mathbb{R})$. As an application, we extend
$B_{\infty 1}^{n}(\mathbb{R})\cap B_{\infty 1}^{1}(\mathbb{R})$. As an application, we extend 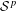 ${\mathcal{S}}^{p}$-estimates for operator Taylor remainders to a broad set of symbols. Finally, we establish explicit formulas for Fréchet differentials and Gâteaux derivatives.
${\mathcal{S}}^{p}$-estimates for operator Taylor remainders to a broad set of symbols. Finally, we establish explicit formulas for Fréchet differentials and Gâteaux derivatives.
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 6 , November 2020 , pp. 1993 - 2016
- Copyright
- © Cambridge University Press 2019
Footnotes
Research supported by the French ‘Investissements d’Avenir’ program, project ISITE-BFC (contract ANR-15-IDEX-03).
Research supported in part by NSF grants DMS-1500704 and DMS-1554456. Corresponding author.
References
- 6
- Cited by





