No CrossRef data available.
Article contents
Stable finite element approximation of a Cahn–Hilliard–Stokes system coupled to an electric field
Published online by Cambridge University Press: 09 September 2016
Abstract
We consider a fully practical finite element approximation of the Cahn–Hilliard–Stokes system:
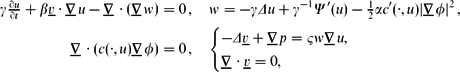 $$\begin{align*}
\gamma \tfrac{\partial u}{\partial t} + \beta v \cdot \nabla u -
\nabla \cdot \left(
\nabla w \right) & = 0 \,, \quad
w= -\gamma \Delta u + \gamma ^{-1} \Psi ' (u) - \tfrac12 \alpha c'(\cdot,u)
| \nabla \phi |^2\,, \\
\nabla \cdot (c(\cdot,u) \nabla \phi) & = 0\,,\quad
\begin{cases}
-\Delta v + \nabla p = \varsigma w \nabla u, \\
\nabla \cdot v = 0, \end{cases}
\end{align*}$$
$$\begin{align*}
\gamma \tfrac{\partial u}{\partial t} + \beta v \cdot \nabla u -
\nabla \cdot \left(
\nabla w \right) & = 0 \,, \quad
w= -\gamma \Delta u + \gamma ^{-1} \Psi ' (u) - \tfrac12 \alpha c'(\cdot,u)
| \nabla \phi |^2\,, \\
\nabla \cdot (c(\cdot,u) \nabla \phi) & = 0\,,\quad
\begin{cases}
-\Delta v + \nabla p = \varsigma w \nabla u, \\
\nabla \cdot v = 0, \end{cases}
\end{align*}$$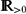 $\mathbb{R}_{>0}$ is the interfacial parameter, α ∈
$\mathbb{R}_{>0}$ is the interfacial parameter, α ∈ 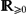 $\mathbb{R}_{\geq0}$ is the field strength parameter, Ψ is the obstacle potential, c(⋅, u) is the diffusion coefficient, and c′(⋅, u) denotes differentiation with respect to the second argument. Furthermore, w is the chemical potential, φ is the electro-static potential, and (v, p) are the velocity and pressure. The system has been proposed to model the manipulation of morphologies in organic solar cells with the help of an applied electric field and kinetics.
$\mathbb{R}_{\geq0}$ is the field strength parameter, Ψ is the obstacle potential, c(⋅, u) is the diffusion coefficient, and c′(⋅, u) denotes differentiation with respect to the second argument. Furthermore, w is the chemical potential, φ is the electro-static potential, and (v, p) are the velocity and pressure. The system has been proposed to model the manipulation of morphologies in organic solar cells with the help of an applied electric field and kinetics.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2016




