Skip to main content

Advertisement

SpringerLink
Log in

Suppression and stability analysis of frequency coupling effect in grid-connected inverters

  • Original Article
  • Published:
Journal of Power Electronics Aims and scope Submit manuscript

Abstract

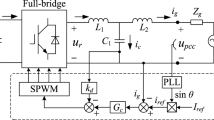
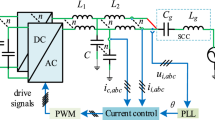
With the proposal of the “dual carbon target” in China, the rapid development of renewable energy, mainly photovoltaic and wind power, has been promoted. However, a large amount of renewable energy connected to a grid results in its proportion in the power system going from a low state to a high state. Under a high proportion, the asymmetry of the control structure or parameters in the three-phase grid-connected inverter controller lead to a strong coupling relationship between the sub/super synchronous frequency components, or frequency coupling effect (FCE). This phenomenon can deteriorate the power quality of the inverter system, amplify the harm of frequency oscillation, and even cause system disassembly. To solve the above problems, a unified impedance model considering the FCE induced by the phase-locked loop (PLL), the current loop (CL), and the power outer loop (POL) is established. Based on the established output impedance model, a parameter optimization theoretical analysis method is designed considering the critical stability of the PLL bandwidth and the CL asymmetry degree. Meanwhile, an improved control strategy for the PLL and the POL is proposed. Experimental results show that the proposed parameter optimization and structure improvement strategies can effectively suppress the influence of frequency coupling and enhance system stability. Finally, simulation and experimental results verify the correctness of the theoretical analysis and the effectiveness of the proposed strategy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Data availability

The paper has attached all the data.

References

  1. Xie, X.R., He, J.B., Mao, H.Y., Li, H.Z.: New issues and classification of power system stability with high shares of renewables and power electronics. Proc. CSEE. 41(02), 461–475 (2021)

    Google Scholar 

  2. Zhang, X., Xia, D., Fu, Z., Wang, G., Xu, D.: An improved feedforward control method considering PLL dynamics to improve weak grid stability of grid-connected inverters. IEEE Trans. Ind. Appl. 54(5), 5143–5151 (2018)

    Article  Google Scholar 

  3. Sun, H.D., Xu, T., Guo, Q., Li, Y.L., et al.: Analysis on blackout in great Britain power grid on August 9th, 2019 and its enlightenment to power grid in China. Proc. CSEE. 39(21), 6183–6192 (2019)

    Google Scholar 

  4. Li, M.J., Yu, Z., Xu, T., He, J.B., Wang, C., Xie, X.R., Liu, C.: Study of complex oscillation caused by renewable energy integration and its solution. Power Grid Technol. 41(04), 1035–1042 (2017)

    Google Scholar 

  5. Ma, N.N., Xie, X.R., He, J.B., Wang, H.: Review of wide-band oscillation in renewable and power electronics highly integrated power systems. Proc. CSEE. 40(15), 4720–4732 (2020)

    Google Scholar 

  6. Sun, J., Li, M.J., Zhang, Z.G., Xu, T., He, J.B., Wang, H.J., Li, G.H.: Renewable energy transmission by HVDC across the continent: system challenges and opportunities. CSEE J. Power Energy Syst. 3(4), 353–364 (2017)

    Article  Google Scholar 

  7. Xie, X.R., Liu, H.K., He, J.B., Zhang, C.Y., Qiao, Y.: Mechanism and characteristics of subsynchronous oscillation caused by the interaction between full-converter wind turbines and AC systems. Proc. CSEE. 36(9), 2366–2372 (2016)

    Google Scholar 

  8. Du, C.M., Du, X., Zou, X.M., Tang, J.C.: Impedance modeling and stability analysis of grid-connected modular multilevel converter considering frequency coupling effect. Proc. CSEE. 40(09), 2866–2877 (2020)

    Google Scholar 

  9. Rygg, A., Molinas, M., Zhang, C., Cai, X.: A modified sequence-domain impedance definition and its equivalence to the dq-domain impedance definition for the stability analysis of AC power electronic systems. IEEE J. Emerg. Sel. Topics Power Electron. 4(4), 1383–1396 (2016)

    Article  Google Scholar 

  10. Bakhshizadeh, M.K., Wang, F.X., Blaabjerg, F., Hjerrild, J., Kocewiak, Ł, Bak, C.L., Hesselbek, B.: Couplings in phase domain impedance modelling of grid-connected converters. IEEE Trans. Power Electron. 31(10), 6792–6796 (2016)

    Google Scholar 

  11. Liu, W., Xie, X.R., Huang, J.K., Zhang, C.Y., Yin, C.Q.: Frequency-coupled impedance model and stability analysis of grid-connected converter. Autom. Electr. Power Syst. 43(03), 138–146 (2019)

    Google Scholar 

  12. Nian, H., Xu, Y.Y., Chen, L., Li, G.H.: Frequency coupling characteristic modeling of grid-connected inverter and system stability analysis. Proc. CSEE. 39(05), 1421–1432 (2019)

    Google Scholar 

  13. Harnefors, L., Bongiorno, M., Lundberg, S.: Input-admittance calculation and shaping for controlled voltage-source converters. IEEE Trans. Industr. Electron. 54(6), 3323–3334 (2007)

    Article  Google Scholar 

  14. Wu, C., Hu, B., Cheng, P., Nian, H., Blaabjerg, F.: Eliminating Frequency Coupling of DFIG System Using a Complex Vector PLL. 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), 3262–3266 (2020)

  15. Céspedes, M., Sun, J.: Impedance shaping of three-phase grid-parallel voltage-source converters. in 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), 754–760 (2012)

  16. Wu, X.Q., Wang, Y.C., Chen, X., Chen, J., et al.: Sequence impedance model and interaction stability research of three-phase grid-connected inverters with considering coupling effects. Proc CSEE. 40(05), 1605–1617 (2020)

    Google Scholar 

  17. Wu, W.H., Zhou, L.M., Chen, Y.D., Luo, A., et al.: Stability comparison and analysis between the virtual synchronous generator and the traditional grid-connected inverter in the view of sequence impedance. Proc CSEE. 39(05), 1411–1421 (2019)

    Google Scholar 

  18. Kazem Bakhshizadeh, M., et al.: Couplings in phase domain impedance modeling of grid-connected converters. IEEE Trans. Power Electron. 31(10), 6792–6796 (2016)

    Google Scholar 

  19. Wen, B., Boroyevich, D., Mattavelli, P., Shen, Z. Y., Burgos, R.: Influence of phase-locked loop on input admittance of three-phase voltage-source converters. 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), 897–904 (2013)

  20. Chen, X., Wang, Y.C., Gong, C.Y., Sun, J., et al.: Overview of stability research for grid-connected inverters based on impedance analysis method. Proc. CSEE. 38(07), 2082–2094+2223 (2018)

    Google Scholar 

Download references

Acknowledgements

This research was supported by the National Natural Science Foundation of China (NSFC) (Fund Number: 52077191, 62003297).

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, Yanshan University, Qinhuangdao, Hebei, China

    Xiaohuan Wang, Aihua Yang, Yang Liu & Xiaojun Zhao

Authors
  1. Xiaohuan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Aihua Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yang Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiaojun Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Aihua Yang.

Appendix

Appendix

$$\begin{gathered} A_{11} = s_{p} L + K_{m} V_{dc} (H_{i} (s_{p} - s_{0} ) - jk_{d} ) \hfill \\ {\kern 1pt} A_{12} = K_{m} V_{dc} H_{i}^{\sim } (s_{p} - s_{0} ) \hfill \\ A_{21} = K_{m} V_{dc} H_{i}^{\sim } (s_{p} - s_{0} ){\kern 1pt} \hfill \\ {\kern 1pt} {\kern 1pt} A_{22} = s_{p2} L + K_{m} V_{dc} (H_{i} (s_{p} - s_{0} ) + jk_{d} ), \hfill \\ \end{gathered}$$
(A1)

where Eq. (A1) is the output impedance element that is partially affected by the CL only when the CL considers the FCE. In addition, A11 reflects the effect of the positive sequence voltage disturbance on the response of the positive sequence current; A12 reflects the effect of the positive sequence voltage disturbance on the response of the coupling current; A21 reflects the effect of the coupling voltage disturbance on the response of the positive sequence current; and A22 reflects the effect of the coupling voltage disturbance on the response of the coupling current, where Km indicates the inverter gain.

$$\begin{gathered} B_{11} = K_{m} V_{dc} T_{PLL} (s_{p} - s_{0} )[(H_{i} (s_{p} - s_{0} ) - jk_{d} )I_{1} \\ {\kern 1pt} {\kern 1pt} - H_{i}^{\sim } (s_{p} - s_{0} )I_{1}^{*} + M_{1} ] \\ B_{12} = - K_{m} V_{dc} T_{PLL} (s_{p} - s_{0} )[(H_{i} (s_{p} - s_{0} ) - jk_{d} )I_{1} \\ {\kern 1pt} - H_{i}^{\sim } (s_{p} - s_{0} )I_{1}^{*} + M_{1} ] \\ B_{21} = - K_{m} V_{dc} T_{PLL} (s_{p} - s_{0} )[(H_{i} (s_{p} - s_{0} ) + jk_{d} )I_{1}^{*} \\ {\kern 1pt} - H_{i}^{\sim } (s_{p} - s_{0} )I_{1} + M_{1}^{*} ] \\ B_{22} = K_{m} V_{dc} T_{PLL} (s_{p} - s_{0} )[(H_{i} (s_{p} - s_{0} ) + jk_{d} )I_{1}^{*} \\ {\kern 1pt} {\kern 1pt} - H_{i}^{\sim } (s_{p} - s_{0} )I_{1} + M_{1}^{*} ], \\ \end{gathered}$$
(A2)

where Eq. (A2) represents the corresponding output impedance matrix elements affected by the PLL when the CL and PLL are considered for the FCE. In addition, the variable elements B11, B12, B21, and B22 in the matrix represent the effects of the disturbance voltages Vp and Vp2 through the PLL on the inverter output voltage.

$$\begin{gathered} E_{ip} = \frac{3}{4}H_{di} \left( {s_{p} } \right)G_{p} \left( {s_{p} - s_{0} } \right)\mathop {\mathop V\limits^{.} }\nolimits_{1}^{*} + \frac{3}{4}H_{qi} \left( {s_{p} } \right)G_{q} \left( {s_{p} - s_{0} } \right)\left( { - \mathop {\mathop V\limits^{.} }\nolimits_{1}^{*} } \right) \hfill \\ E_{ip2} = \frac{3}{4}H_{di} \left( {s_{p} } \right)G_{p} \left( {s_{p} - s_{0} } \right)\mathop {\mathop V\limits^{.} }\nolimits_{1}^{{}} + \frac{3}{4}H_{qi} \left( {s_{p} } \right)G_{q} \left( {s_{p} - s_{0} } \right)\mathop {\mathop V\limits^{.} }\nolimits_{1}^{{}} \hfill \\ F_{vp} = \frac{3}{4}H_{di} \left( {s_{p2} } \right)G_{p} \left( {s_{p2} - s_{0} } \right)\mathop {\mathop I\limits^{.} }\nolimits_{1}^{*} + \frac{3}{4}H_{qi} \left( {s_{p2} } \right)G_{q} \left( {s_{p2} - s_{0} } \right)\mathop {\mathop I\limits^{.} }\nolimits_{1}^{*} \hfill \\ F_{vp2} = \frac{3}{4}H_{di} \left( {s_{p2} } \right)G_{p} \left( {s_{p2} - s_{0} } \right)\mathop {\mathop I\limits^{.} }\nolimits_{1}^{{}} + \frac{3}{4}H_{qi} \left( {s_{p2} } \right)G_{q} \left( {s_{p2} - s_{0} } \right)\left( { - \mathop {\mathop I\limits^{.} }\nolimits_{1}^{{}} } \right), \hfill \\ \end{gathered}$$
(A3)

where Eq. (A3) represents the elements of the output matrix corresponding to being partially affected by the POL when the CL, PLL, and POL are considered for frequency coupling effects. The variables Eip, Eip2, Fvp, and Fvp2 represent the effects of the perturbation voltages Vp and Vp2 passing through the POL on the output current components.

$$Z_{i} = 1/Y_{i} = sL + K_{m} V_{dc} (H_{i} - jk_{d} )$$
(A4)
$$Y_{I} = {{(\frac{1}{2}K_{m} V_{dc} T_{PLL} H_{i}^{\sim } I_{1} )} \mathord{\left/ {\vphantom {{(\frac{1}{2}K_{m} V_{dc} T_{PLL} H_{i}^{\sim } I_{1} )} {[sL + K_{m} V_{dc} (H_{i} - jk_{d} )]}}} \right. \kern-0pt} {[sL + K_{m} V_{dc} (H_{i} - jk_{d} )]}}$$
(A5)
$$Y_{PLL} = \frac{{ - K_{m} V_{dc} T_{PLL} [(H_{i} - jk_{d} )I_{1} + M_{1} ]}}{{2[sL + K_{m} V_{dc} (H_{i} - jk_{d} )]}}$$
(A6)
$$\begin{gathered} B_{11}^{^{\prime}} = K_{m} V_{dc} T_{PLL} (s_{p} - s_{0} )[(H_{i} (s_{p} - s_{0} ) - jk_{d} )I_{1} + M_{1} ] \hfill \\ B_{12}^{^{\prime}} = - K_{m} V_{dc} T_{PLL} (s_{p} - s_{0} )[(H_{i} (s_{p} - s_{0} ) - jk_{d} )I_{1} + M_{1} ] \hfill \\ B_{21}^{^{\prime}} = - K_{m} V_{dc} T_{PLL} (s_{p} - s_{0} )[(H_{i} (s_{p} - s_{0} ) + jk_{d} )I_{1}^{*} + M_{1}^{*} ] \hfill \\ B_{22}^{^{\prime}} = K_{m} V_{dc} T_{PLL} (s_{p} - s_{0} )[(H_{i} (s_{p} - s_{0} ) + jk_{d} )I_{1}^{*} + M_{1}^{*} ] \hfill \\ \end{gathered}$$
(A7)

Equation (A7) represents the impedance matrix elements affected by the PLL part of the system output only when the PLL considers the frequency coupling effect. The variable elements \({{B}^{\mathrm{^{\prime}}}}_{11}\), \({{B}^{\mathrm{^{\prime}}}}_{12}\), \({{B}^{\mathrm{^{\prime}}}}_{21}\) and \({{B}^{\mathrm{^{\prime}}}}_{22}\) have the same influence as in Eq. (A2).

$$\begin{gathered} Z_{g} (s_{p} ) = Z_{eq} (s_{p} ) = 1/((Y_{p} - \frac{{{\text{Y}}_{12} (s_{p2} )Y_{21} (s_{p} )}}{{Y_{g} (s_{p2} ) + Y_{22} (s_{p2} )}})) \\ = 1/(\frac{{1 - \frac{1}{2}K_{m} V_{dc} \frac{{m_{0} k_{pp} /s(1 + m_{0} k_{pi} /sk_{pp} )}}{{1 + V_{1} m_{0} k_{pp} /s(1 + m_{0} k_{pi} s/k_{pp} )}}[(H_{i} - jk_{d} )I_{1} + M_{1} ]}}{{s_{p} L + K_{m} V_{dc} (H_{i} - jk_{d} )}} - \frac{{{\text{Y}}_{12} (s_{p2} )Y_{21} (s_{p} )}}{{Y_{g} (s_{p2} ) + Y_{22} (s_{p2} )}}) \\ \end{gathered}$$
(A8)
$$\begin{gathered} Arg\left[ {Z_{g} (s,m_{0} )Y_{eq} (s,m_{0} )} \right] \\ = \angle Z_{g} (s_{p} ) - \\ \angle (\frac{{1 - \frac{1}{2}K_{m} V_{dc} \frac{{m_{0} k_{pp} /s(1 + m_{0} k_{pi} /sk_{pp} )}}{{1 + V_{1} m_{0} k_{pp} /s(1 + m_{0} k_{pi} s/k_{pp} )}}[(H_{i} - jk_{d} )I_{1} + M_{1} ]}}{{s_{p} L + K_{m} V_{dc} (H_{i} - jk_{d} )}} - \frac{{{\text{Y}}_{12} (s_{p2} )Y_{21} (s_{p} )}}{{Y_{g} (s_{p2} ) + Y_{22} (s_{p2} )}}) \\ = 180^{ \circ } \\ \end{gathered}$$
(A9)
$$\begin{gathered} Z_{g} (s_{p} ) = Z_{eq} (s_{p} ) = 1/((Y_{p} - \frac{{{\text{Y}}_{12} (s_{p2} )Y_{21} (s_{p} )}}{{Y_{g} (s_{p2} ) + Y_{22} (s_{p2} )}})) \\ = 1/(\frac{{1 + \frac{1}{2}K_{m} V_{dc} \frac{{n_{0} k_{pp} /s(1 + n_{0} k_{pi} /sk_{pp} )}}{{1 + V_{1} n_{0} k_{pp} /s(1 + n_{0} k_{pi} s/k_{pp} )}}H_{i}^{\sim } I_{1} }}{{sL + K_{m} V_{dc} (H_{i} - jk_{d} )}} - \frac{{{\text{Y}}_{12} (s_{p2} )Y_{21} (s_{p} )}}{{Y_{g} (s_{p2} ) + Y_{22} (s_{p2} )}}) \\ \end{gathered}$$
(A10)
$$\begin{gathered} Arg\left[ {Z_{g} (s,n_{0} )Y_{eq} (s,n_{0} )} \right] = \angle Z_{g} (s_{p} ) - \angle (\frac{{1 + \frac{1}{2}K_{m} V_{dc} \frac{{n_{0} k_{pp} /s(1 + n_{0} k_{pi} /sk_{pp} )}}{{1 + V_{1} n_{0} k_{pp} /s(1 + n_{0} k_{pi} s/k_{pp} )}}H_{i}^{\sim } I_{1} }}{{sL + K_{m} V_{dc} (H_{i} - jk_{d} )}} - \frac{{{\text{Y}}_{12} (s_{p2} )Y_{21} (s_{p} )}}{{Y_{g} (s_{p2} ) + Y_{22} (s_{p2} )}}) = 180^{ \circ } \hfill \\ \angle (\frac{{1 + \frac{1}{2}K_{m} V_{dc} \frac{{n_{0} k_{pp} /s(1 + n_{0} k_{pi} /sk_{pp} )}}{{1 + V_{1} n_{0} k_{pp} /s(1 + n_{0} k_{pi} s/k_{pp} )}}H_{i}^{\sim } I_{1} }}{{sL + K_{m} V_{dc} (H_{i} - jk_{d} )}} - \frac{{{\text{Y}}_{12} (s_{p2} )Y_{21} (s_{p} )}}{{Y_{g} (s_{p2} ) + Y_{22} (s_{p2} )}}) = - 90^{ \circ } \hfill \\ \end{gathered}$$
(A11)

Equations (A8) and (A9) are the tuning formulas for the bandwidth boundary of the PLL considering the frequency coupling effect, and Eqs. (A10) and (A11) are the tuning formulas for the critical asymmetry degree of the current loop considering the frequency coupling effect. These four equations are quoted from Eq. (3) in [20].

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, X., Yang, A., Liu, Y. et al. Suppression and stability analysis of frequency coupling effect in grid-connected inverters. J. Power Electron. 23, 945–958 (2023). https://doi.org/10.1007/s43236-023-00591-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s43236-023-00591-6

Keywords

Search

Navigation